- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Интегральное исчисление. Дифференциальные уравнения презентация
Содержание
- 1. Интегральное исчисление. Дифференциальные уравнения
- 2. Элементы интегрального исчисления 1.Первообразная и неопределенный интеграл
- 3. Первообразная и неопределенный интеграл
- 4. Первообразная и неопределенный интеграл
- 5. Неопределенный интеграл Определение 1. Функция
- 6. Неопределенный интеграл Теорема (о разности первообразных).
- 7. Неопределенный интеграл Следствие. Пусть
- 8. Свойства интеграла, вытекающие из определения
- 9. Свойства интеграла, вытекающие из определения
- 10. Свойства интеграла
- 11. Таблица неопределенных интегралов
- 12. Таблица неопределенных интегралов
- 13. Интегрирование по частям
- 14. Метод замены переменной
- 15. Задача о вычислении площади плоской фигуры
- 16. Задача о вычислении площади плоской фигуры
- 17. Задача о вычислении площади плоской фигуры
- 18. Определенный интеграл
- 19. Определенный интеграл
- 20. Определенный интеграл
- 21. Теорема о существовании определенного интеграла
- 22. Свойства определенного интеграла
- 23. Свойства определенного интеграла
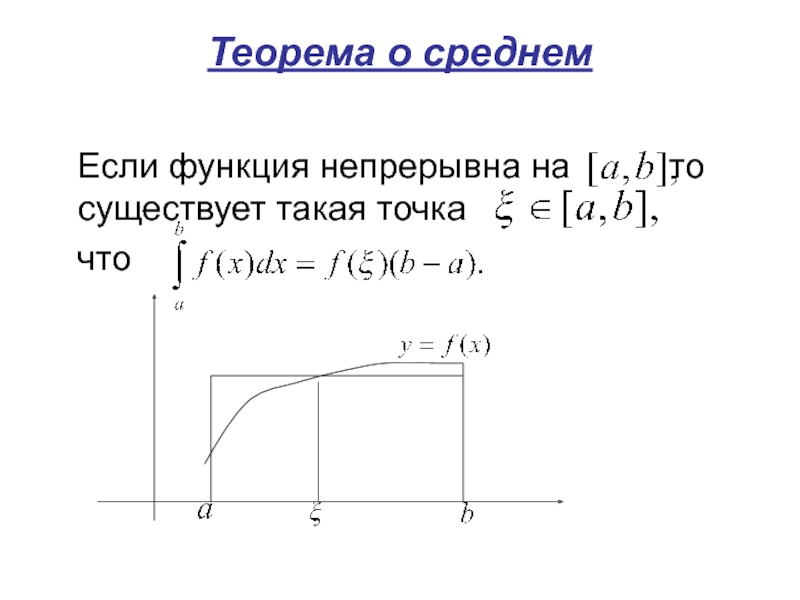
- 24. Теорема о среднем Если функция
- 25. Вычисление определенного интеграла
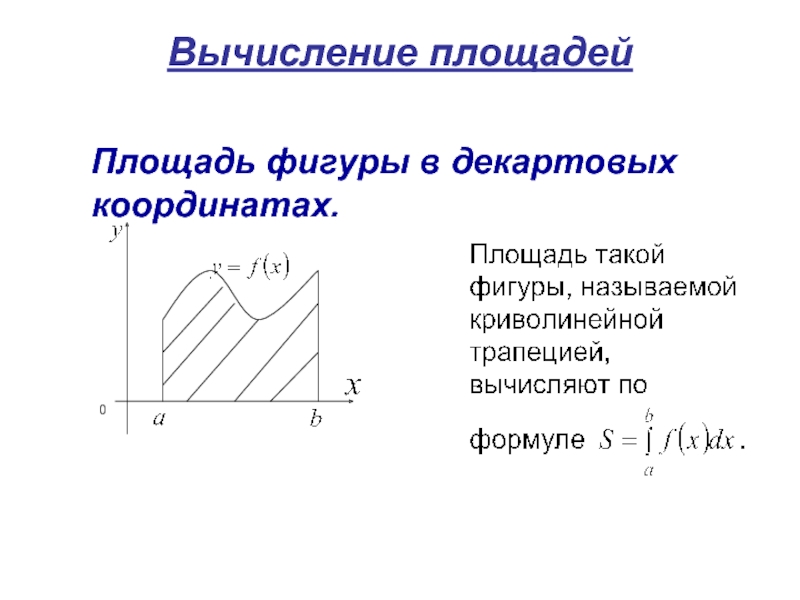
- 26. Вычисление площадей Площадь фигуры в декартовых координатах.
- 27. Обыкновенные дифференциальные уравнения
- 28. Уравнение первого порядка Функциональное
- 29. Общее решение дифференциального уравнения 1-го порядка
- 30. Уравнение Ф(x,y,C) =0, определяющее общее
- 31. Постановка задачи Коши Задача отыскания
- 32. Уравнение с разделяющимися переменными Дифференциальное
- 33. Дифференциальное уравнение 1-го порядка называется
- 34. Однородные уравнения Дифференциальное уравнение первого
- 35. Линейные уравнения 1-го порядка
- 36. Уравнение Бернулли Уравнением Бернулли называется
- 37. Основные понятия Уравнение 2-го порядка
- 38. Задача Коши для уравнения 2-го порядка
- 39. Теорема существования и единственности решения уравнения 2-го
- 40. Уравнения 2-го порядка, допускающие понижение порядка
- 41. Линейные однородные уравнения Линейным однородным
- 42. Линейное однородное уравнение 2-го порядка с постоянными
- 43. Вывод формул общего решения ЛОУ 2-го порядка
- 44. Случай 2. Если
- 45. Случай 3. Если
- 46. СПАСИБО ЗА ВНИМАНИЕ!
Элементы интегрального исчисления 1.Первообразная и неопределенный интеграл 2.Основные приемы вычисления неопределенных интегралов 3.Интегрирование функций, содержащих квадратный трехчлен 4.Интегрирование дробно-рациональных функций 5.Интегрирование тригонометрических функций 6.Интегрирование некоторых иррациональностей
Слайд 2Элементы интегрального исчисления
1.Первообразная и неопределенный интеграл
2.Основные приемы вычисления неопределенных интегралов
3.Интегрирование
функций, содержащих квадратный трехчлен
4.Интегрирование дробно-рациональных функций
5.Интегрирование тригонометрических функций
6.Интегрирование некоторых иррациональностей
4.Интегрирование дробно-рациональных функций
5.Интегрирование тригонометрических функций
6.Интегрирование некоторых иррациональностей
Слайд 5Неопределенный интеграл
Определение 1.
Функция называется
первообразной для в ,
если определена в и
Пример.
если определена в и
Пример.
Слайд 6Неопределенный интеграл
Теорема (о разности первообразных).
Доказательство.
Обозначим через
Пусть
Функция
удовлетворяет
условиям теоремы Лагранжа:
а)
б)
условиям теоремы Лагранжа:
а)
б)
Слайд 7Неопределенный интеграл
Следствие.
Пусть первообразная для
в .
Тогда любая другая первообразная
Определение 2.
Неопределенным интегралом от
называется совокупность всех первообразных
Пример.
Тогда любая другая первообразная
Определение 2.
Неопределенным интегралом от
называется совокупность всех первообразных
Пример.
Графическая иллюстрация
a
b
x
y
Слайд 8Свойства интеграла, вытекающие из определения
Производная неопределенного интеграла равна подынтегральной
функции, а его дифференциал- подынтегральному выражению. Действительно:
Слайд 9Свойства интеграла, вытекающие из определения
Неопределенный интеграл от дифференциала непрерывно
дифференцируемой функции равен самой этой функции с точностью до постоянной:
3.
так как является первообразной для
3.
так как является первообразной для
Слайд 15Задача о вычислении площади плоской фигуры
Решим задачу о вычислении
площади фигуры, ограниченной графиком функции , отрезками прямых
, и осью Ox.Такую фигуру называют криволинейной трапецией
, и осью Ox.Такую фигуру называют криволинейной трапецией
a
b
Слайд 28Уравнение первого порядка
Функциональное уравнение
F(x,y,y′)
= 0 или y′= f(x,y), связывающее между собой независимую переменную, искомую функцию y(x) и ее производную y′(x), называется дифференциальным уравнением первого порядка.
Слайд 29Общее решение дифференциального уравнения 1-го порядка
Общим решением дифференциального уравнения первого
порядка называется такая функция y = ϕ(x,C), которая при любом значении параметра C является решением этого дифференциального уравнения.
Слайд 30 Уравнение Ф(x,y,C) =0, определяющее общее решение как неявную функцию,
называется общим интегралом дифференциального уравнения первого порядка.
Слайд 31Постановка задачи Коши
Задача отыскания решения дифференциального уравнения
,
удовлетворяющего начальному условию
при , называется задачей Коши для уравнения 1-го порядка.
Слайд 32Уравнение с разделяющимися переменными
Дифференциальное уравнение
называется уравнением с
разделенными переменными.
Слайд 33 Дифференциальное уравнение 1-го порядка называется уравнением с разделяющимися переменными,
если оно имеет вид:
.
Для решения уравнения делят обе его части на произведение функций
,
а затем интегрируют.
.
Для решения уравнения делят обе его части на произведение функций
,
а затем интегрируют.
Уравнение с разделяющимися переменными
Слайд 34Однородные уравнения
Дифференциальное уравнение первого
порядка называется однородным,
если его можно привести к виду y′=
или к виду
где и – однородные функции одного порядка .
или к виду
где и – однородные функции одного порядка .
Слайд 35Линейные уравнения 1-го порядка
Дифференциальное уравнение первого порядка называется
линейным, если оно содержит и в первой степени, т.е. имеет вид
.
Решают такое уравнение с помощью подстановки y=uv, где u и v-вспомогательные неизвестные функции, которые находят, подставляя в уравнение вспомогательные функции и на одну из функций налагают определенные условия.
.
Решают такое уравнение с помощью подстановки y=uv, где u и v-вспомогательные неизвестные функции, которые находят, подставляя в уравнение вспомогательные функции и на одну из функций налагают определенные условия.
Слайд 36Уравнение Бернулли
Уравнением Бернулли называется уравнение 1-го порядка, имеющее вид
,
где и
Его, как и линейное уравнение решают с помощью подстановки
где и
Его, как и линейное уравнение решают с помощью подстановки
Слайд 37Основные понятия
Уравнение 2-го порядка имеет вид
Или
Общим решением уравнения второго порядка называется такая функция , которая при любых значениях параметров является решением этого уравнения.
Слайд 38Задача Коши для уравнения 2-го порядка
Если уравнение 2-го порядка
разрешить относительно второй производной, то для такого уравнения имеет место задача: найти решение уравнения ,
удовлетворяющее начальным условиям:
и
Эту задачу называют задачей Коши для дифференциального уравнения 2-гопорядка.
удовлетворяющее начальным условиям:
и
Эту задачу называют задачей Коши для дифференциального уравнения 2-гопорядка.
Слайд 39Теорема существования и единственности решения уравнения 2-го порядка
Если в
уравнении функция и ее частные производные по аргументам и непрерывны в некоторой области, содержащей точку ,
то существует и притом единственное решение этого уравнения, удовлетворяющее условиям
и .
то существует и притом единственное решение этого уравнения, удовлетворяющее условиям
и .
Слайд 40Уравнения 2-го порядка, допускающие понижение порядка
Простейшее уравнение 2-го порядка
решают двукратным интегрированием.
Уравнение , не содержащее явно у, решают с помощью подстановки ,
Уравнение , не содержащее х, решают заменой
, .
Слайд 41Линейные однородные уравнения
Линейным однородным дифференциальным уравнением второго порядка называется
уравнение .
Если все коэффициенты этого уравнения постоянны, то уравнение называется уравнением с постоянными коэффициентами .
Если все коэффициенты этого уравнения постоянны, то уравнение называется уравнением с постоянными коэффициентами .
Слайд 42Линейное однородное уравнение 2-го порядка с постоянными коэффициентами
Уравнение
называется характеристическим уравнением линейного уравнения .
Оно получается из ЛОУ заменой соотстветствующей порядку производной степенью k .
Оно получается из ЛОУ заменой соотстветствующей порядку производной степенью k .
Слайд 43Вывод формул общего решения ЛОУ 2-го порядка
Корни характеристического уравнения
Случай 1. Если , то
характеристическое уравнение имеет два
различных действительных корня
В этом случае общее решение имеет вид
.
характеристическое уравнение имеет два
различных действительных корня
В этом случае общее решение имеет вид
.
Слайд 44
Случай 2. Если
, то характеристическое уравнение имеет одинаковые корни .
Частные решения ЛОУ выбираем так, чтобы они были линейно независимыми:
и .
Общее решение ЛОУ 2-го порядка будет иметь вид .
Частные решения ЛОУ выбираем так, чтобы они были линейно независимыми:
и .
Общее решение ЛОУ 2-го порядка будет иметь вид .
Слайд 45 Случай 3. Если
, то
характеристическое уравнение имеет два комплексно-сопряженных корня
и , где
и .
Общее решение ЛОУ 2-го порядка в действительной форме можно записать
в виде
характеристическое уравнение имеет два комплексно-сопряженных корня
и , где
и .
Общее решение ЛОУ 2-го порядка в действительной форме можно записать
в виде
