Definitions and examples
Paths and cycles
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Graph theory irina prosvirnina. Definitions and examples. Paths and cycles презентация
Содержание
- 1. Graph theory irina prosvirnina. Definitions and examples. Paths and cycles
- 2. Definitions and examples
- 3. Definitions and examples Euler (1707 – 1783)
- 4. Definitions and examples Like many of the
- 5. Definitions and examples What is a ‘graph’?
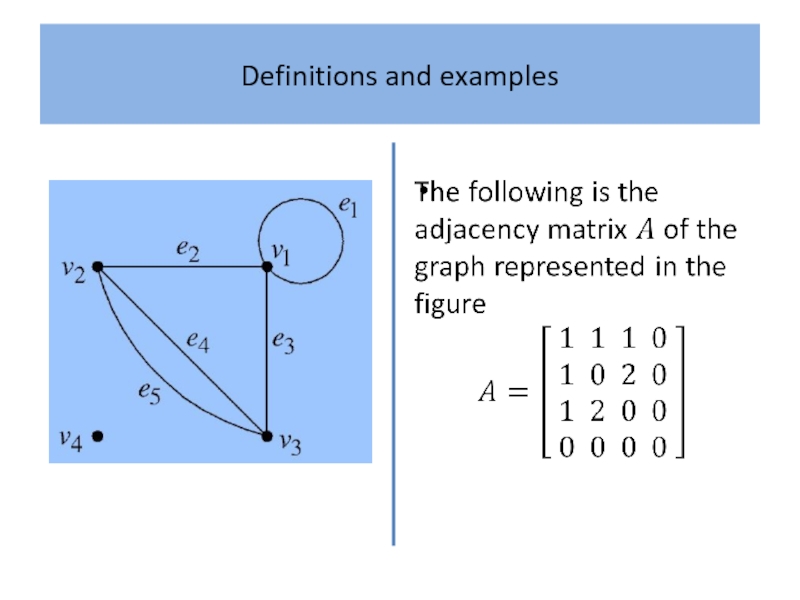
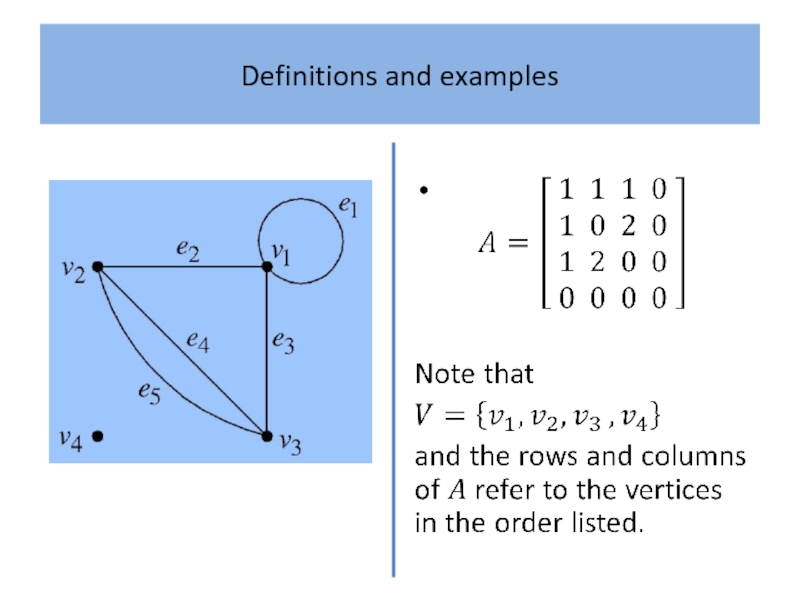
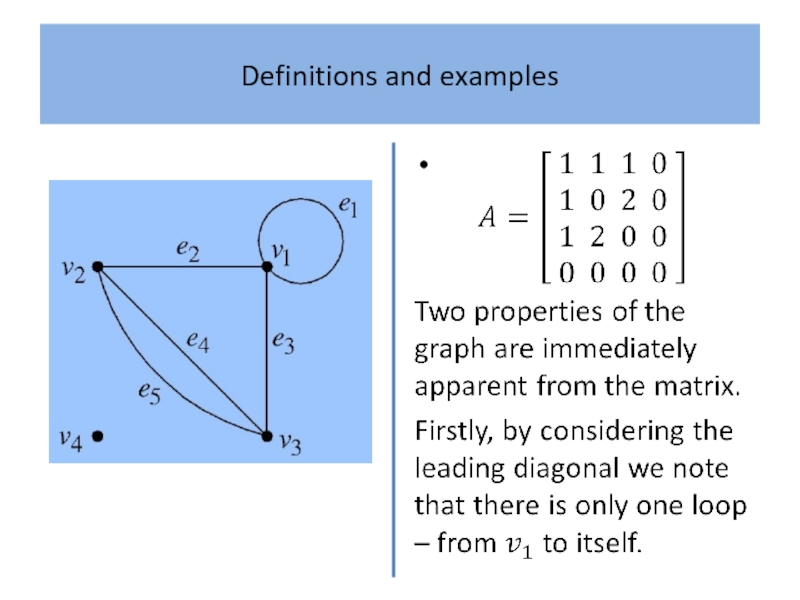
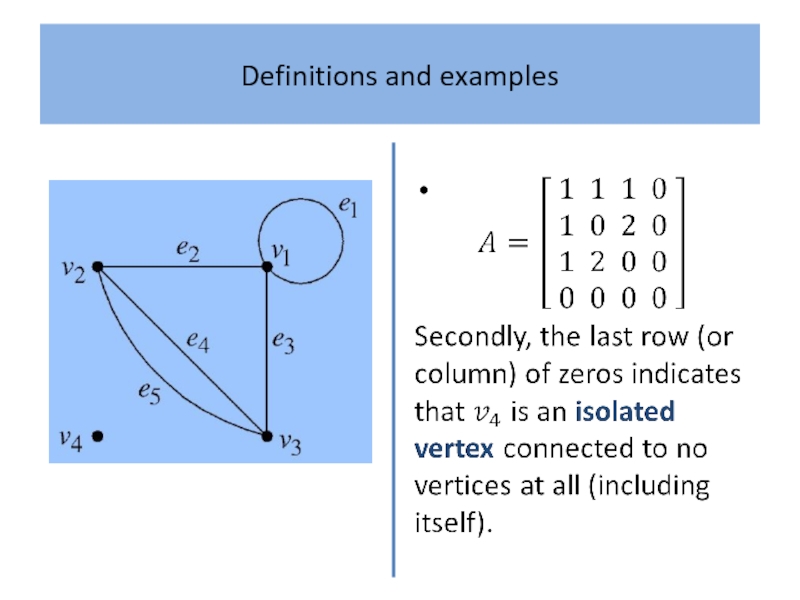
- 6. Definitions and examples
- 7. Definitions and examples
- 8. Definitions and examples
- 9. Definitions and examples
- 10. Definitions and examples
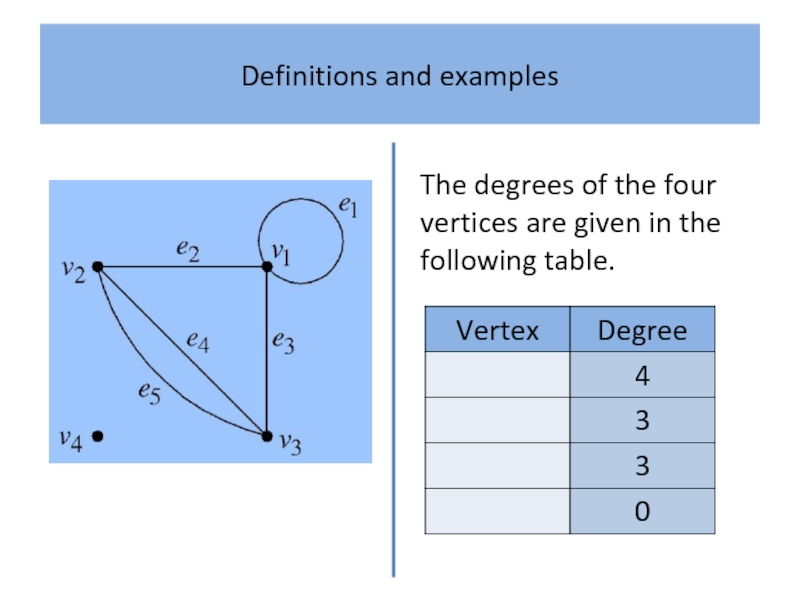
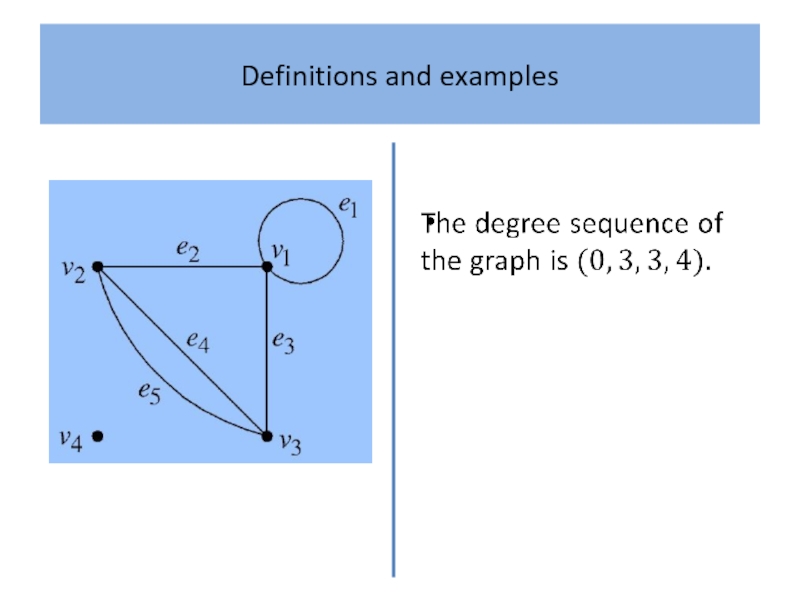
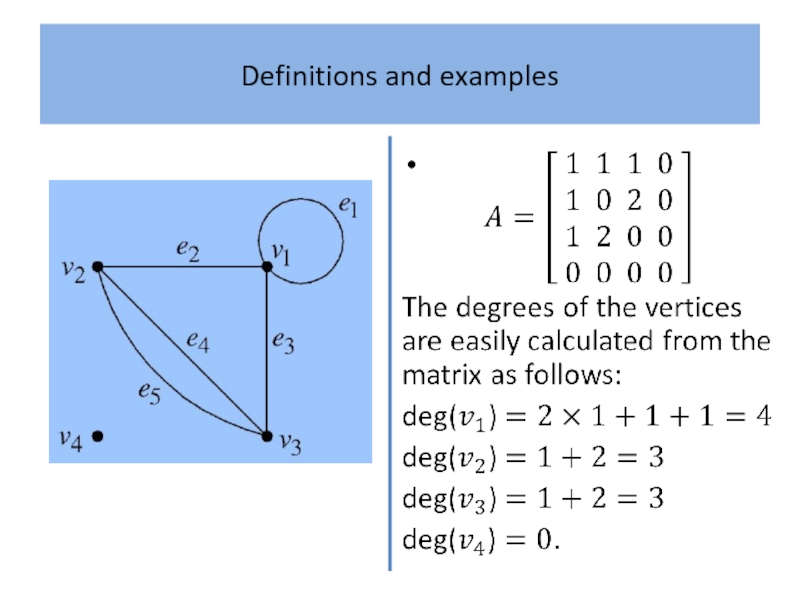
- 11. Definitions and examples Definition 2 The degree
- 12. Definitions and examples
- 13. Definitions and examples
- 14. Definitions and examples
- 15. Definitions and examples
- 16. Definitions and examples
- 17. Definitions and examples
- 18. Definitions and examples Example 1 Since a
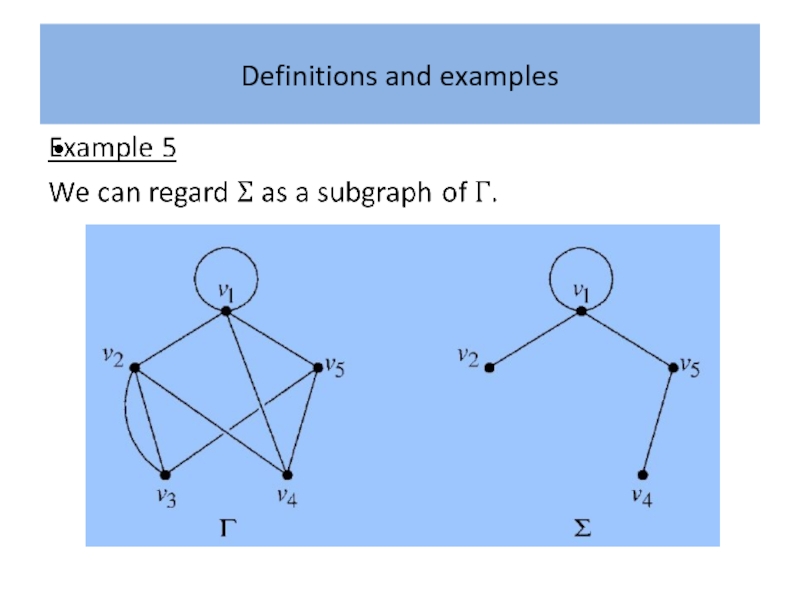
- 19. Definitions and examples
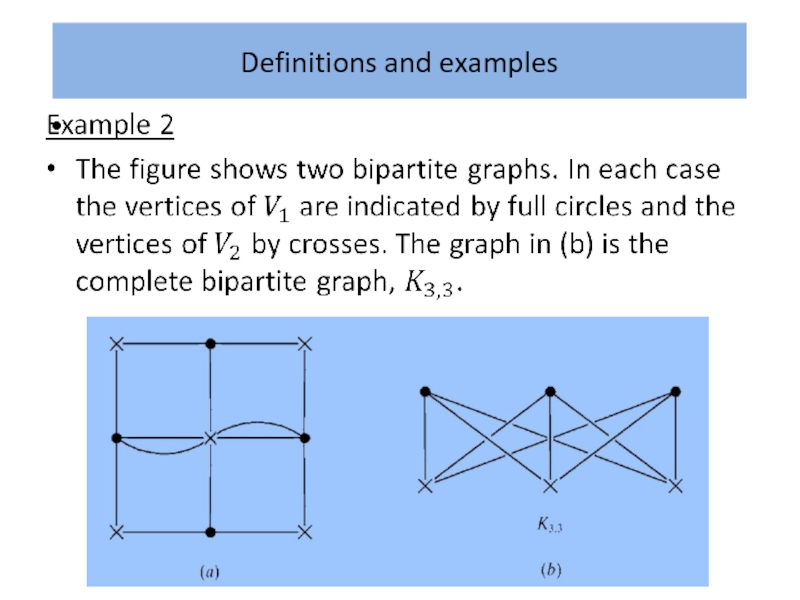
- 20. Definitions and examples Example 1 The complete
- 21. Definitions and examples
- 22. Definitions and examples
- 23. Definitions and examples
- 24. Definitions and examples
- 25. Definitions and examples
- 26. Definitions and examples
- 27. Definitions and examples
- 28. Definitions and examples
- 29. Definitions and examples
- 30. Definitions and examples
- 31. Definitions and examples
- 32. Definitions and examples Example 4 A complete
- 33. Definitions and examples
- 34. Definitions and examples
- 35. Paths and cycles Using the analogy of
- 36. Paths and cycles
- 37. Paths and cycles
- 38. Paths and cycles
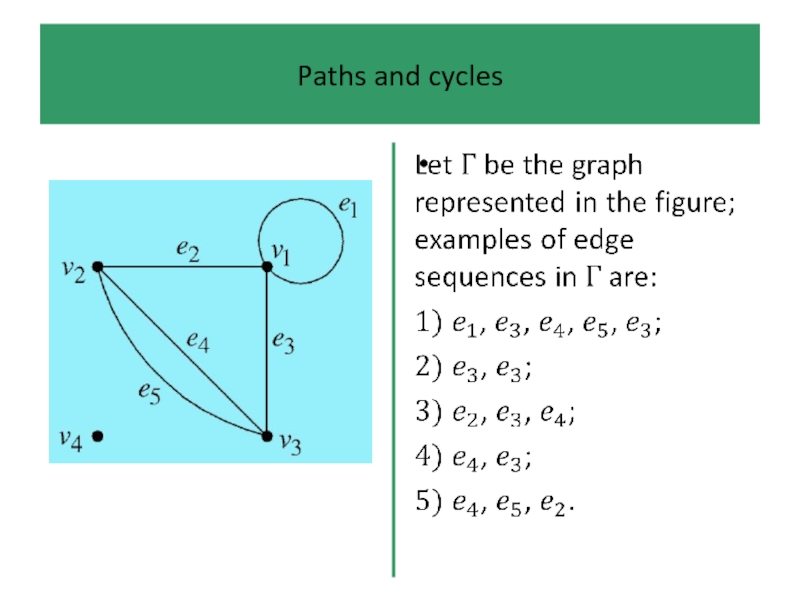
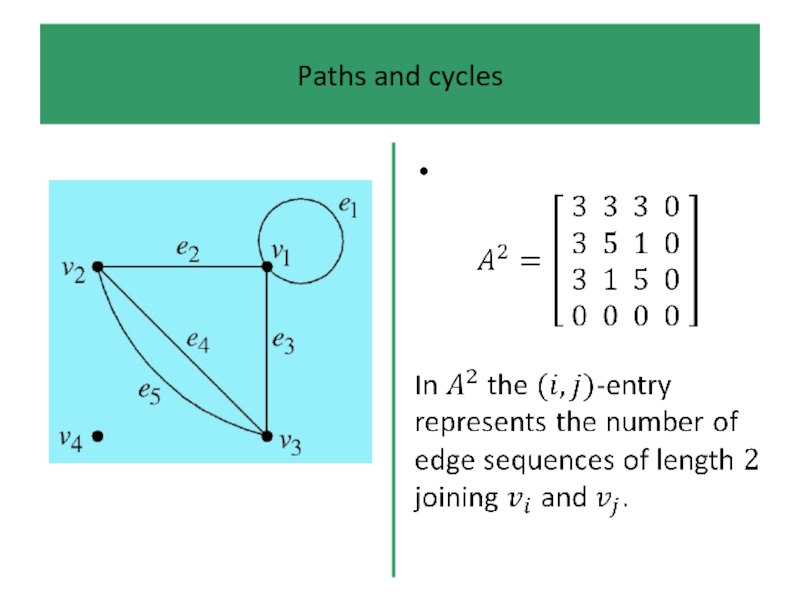
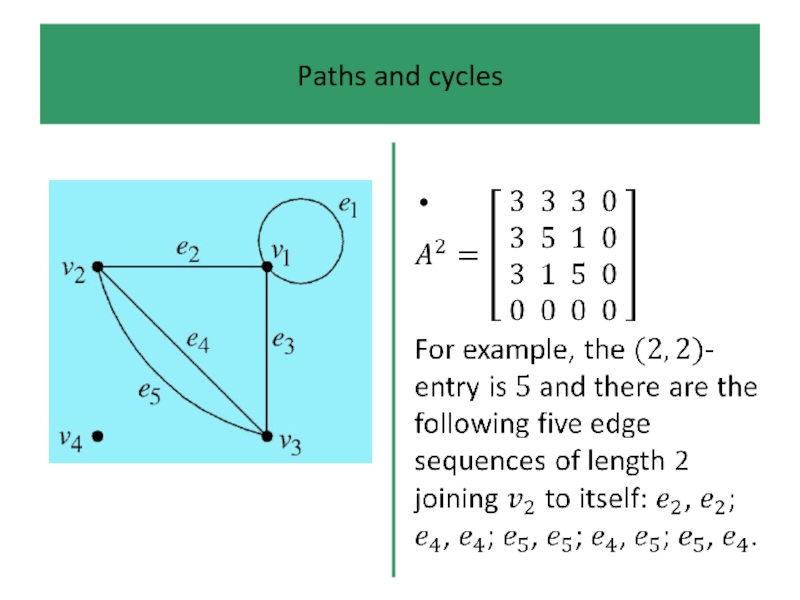
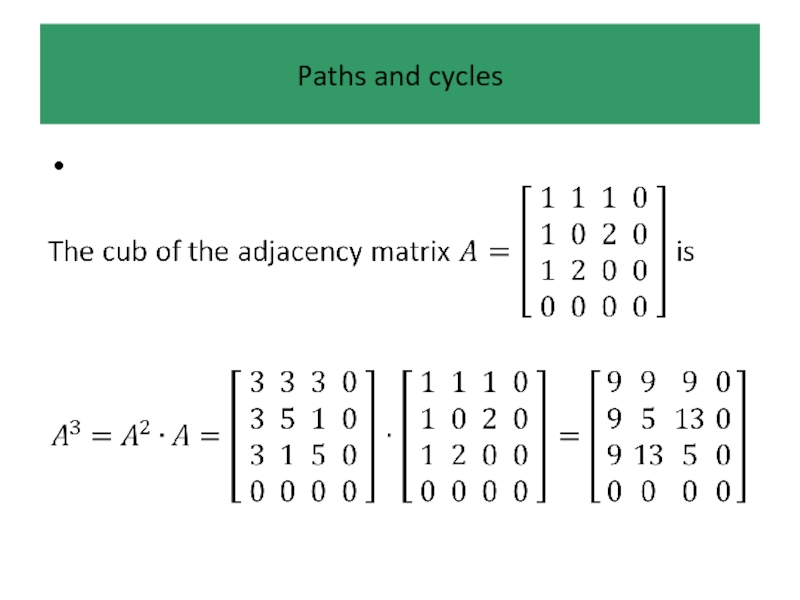
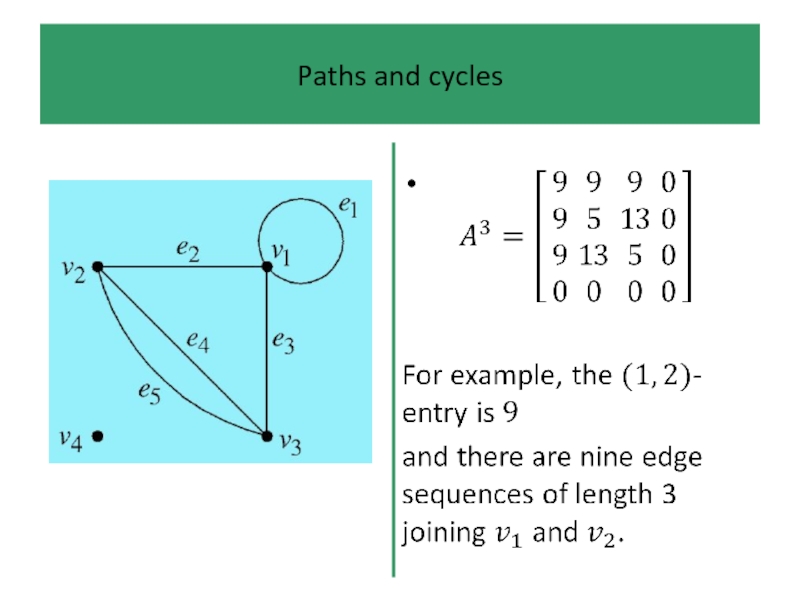
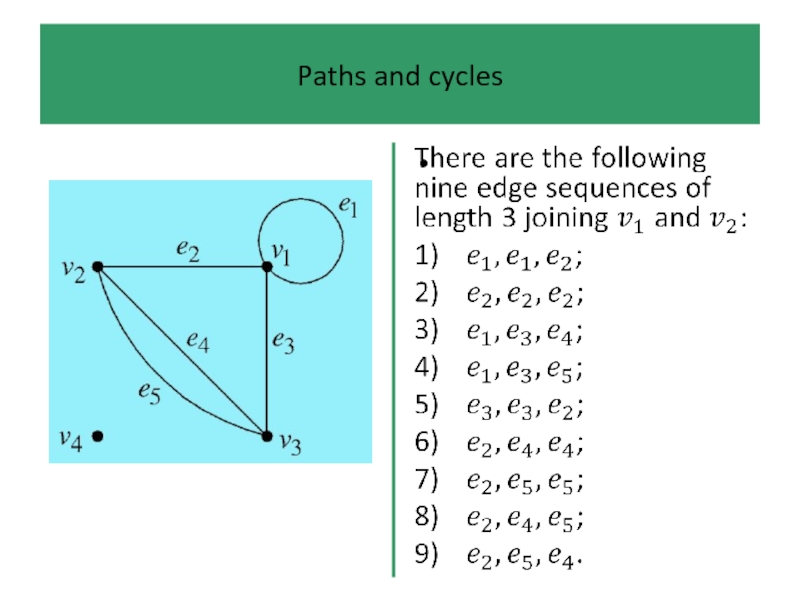
- 39. Paths and cycles An edge sequence is
- 40. Paths and cycles Edge sequences are too
- 41. Paths and cycles In a path we
- 42. Paths and cycles If, in addition, we
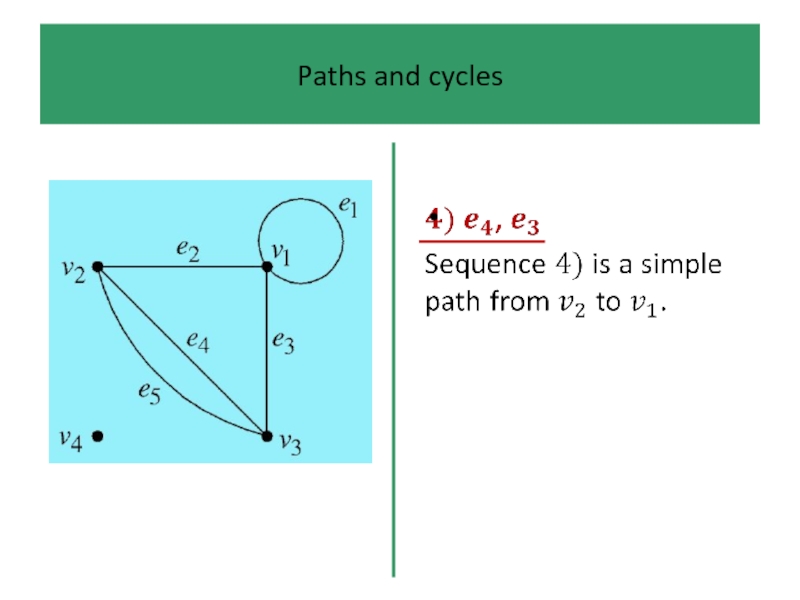
- 43. Paths and cycles The edge sequence or
- 44. Paths and cycles
- 45. Paths and cycles
- 46. Paths and cycles
- 47. Paths and cycles
- 48. Paths and cycles
- 49. Paths and cycles
- 50. Paths and cycles
- 51. Paths and cycles
- 52. Paths and cycles
- 53. Paths and cycles
- 54.
- 55. Paths and cycles
- 56. Paths and cycles
- 57. Paths and cycles
- 58. Paths and cycles
- 59. Paths and cycles In an intuitively obvious
- 60. Paths and cycles Definition 7 A graph
- 61. Paths and cycles An arbitrary graph naturally
- 62. Paths and cycles
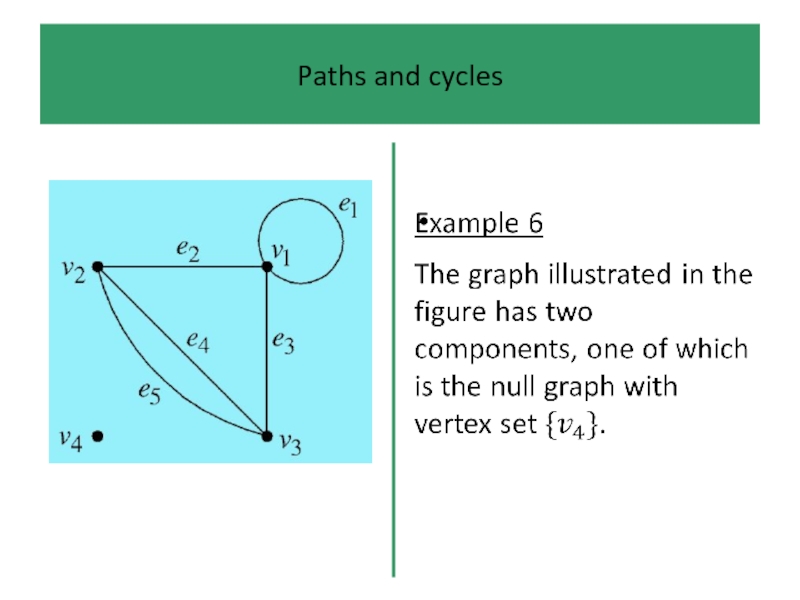
- 63. Paths and cycles The components of a
- 64. Paths and cycles
- 65. Paths and cycles
- 66. Paths and cycles
- 67. Paths and cycles
- 68. Paths and cycles
Слайд 3Definitions and examples
Euler (1707 – 1783) was born in Switzerland and
spent most of his long life in Russia (St Petersburg) and Prussia (Berlin).
He was the most prolific mathematician of all time, his collected works filling more than 70 volumes.
He was the most prolific mathematician of all time, his collected works filling more than 70 volumes.
Слайд 4Definitions and examples
Like many of the very great mathematicians of his
era, Euler contributed to almost every branch of pure and applied mathematics.
He is also responsible, more than any other person, for much of the mathematical notation in use today.
He is also responsible, more than any other person, for much of the mathematical notation in use today.
Слайд 5Definitions and examples
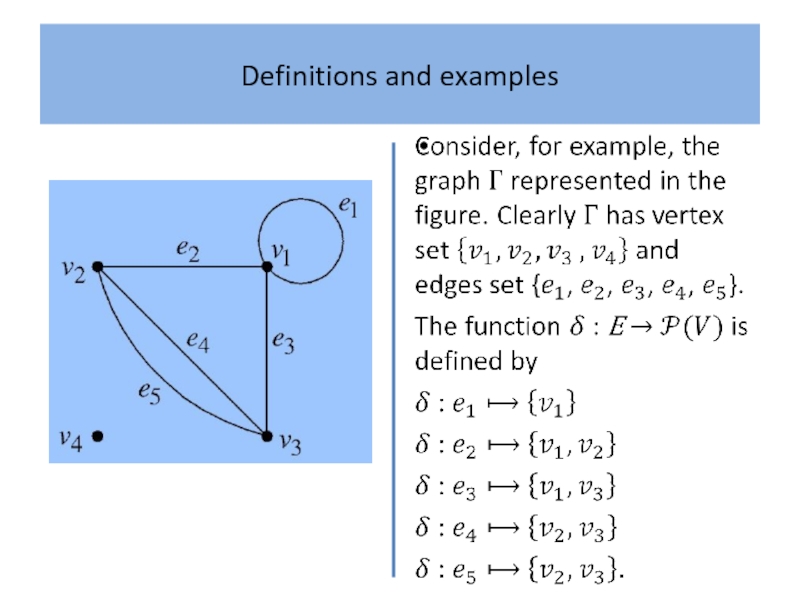
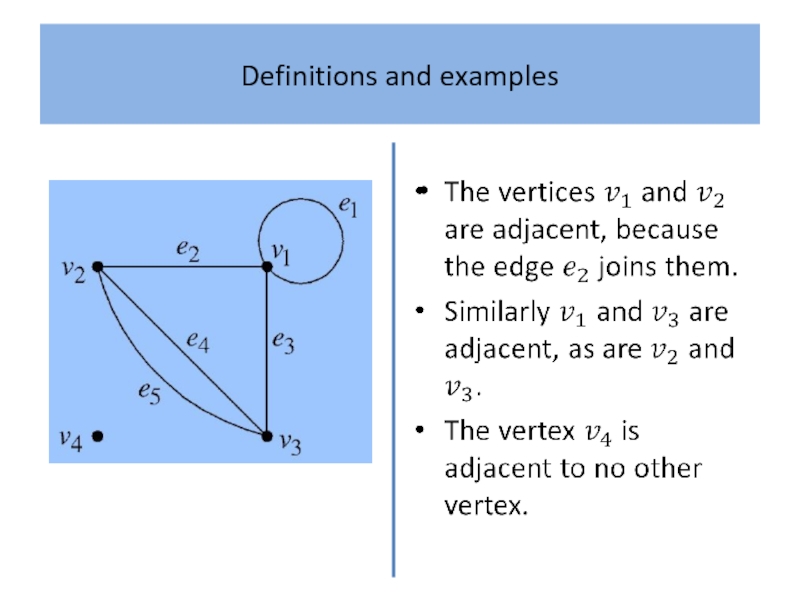
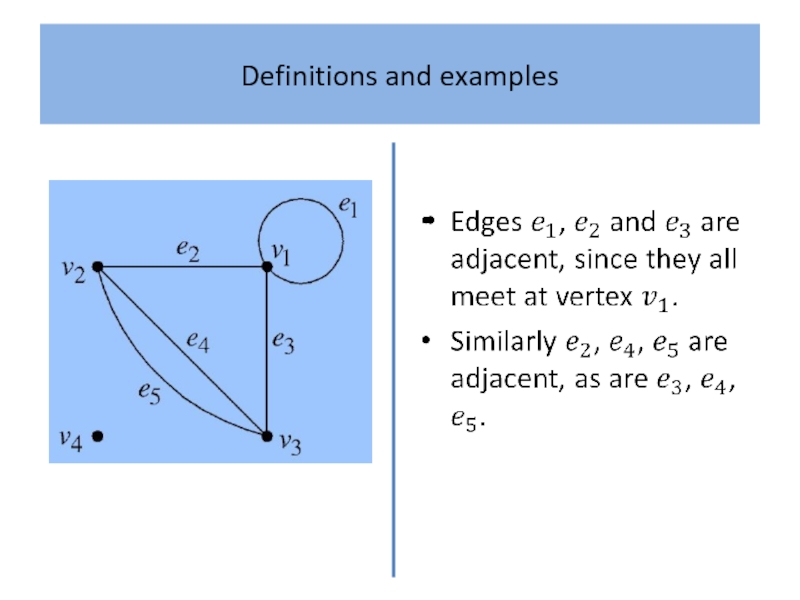
What is a ‘graph’? Intuitively, a graph is simply
a collection of points, called ‘vertices’, and a collection of lines, called ‘edges’, each of which joins either a pair of points or a single point to itself.
A familiar example, which serves as a useful analogy, is a road map which shows towns as vertices and the roads joining them as edges.
A familiar example, which serves as a useful analogy, is a road map which shows towns as vertices and the roads joining them as edges.
Слайд 11Definitions and examples
Definition 2
The degree sequence of a graph is the
sequence of its vertex degrees arranged in non-decreasing order.
Слайд 16Definitions and examples
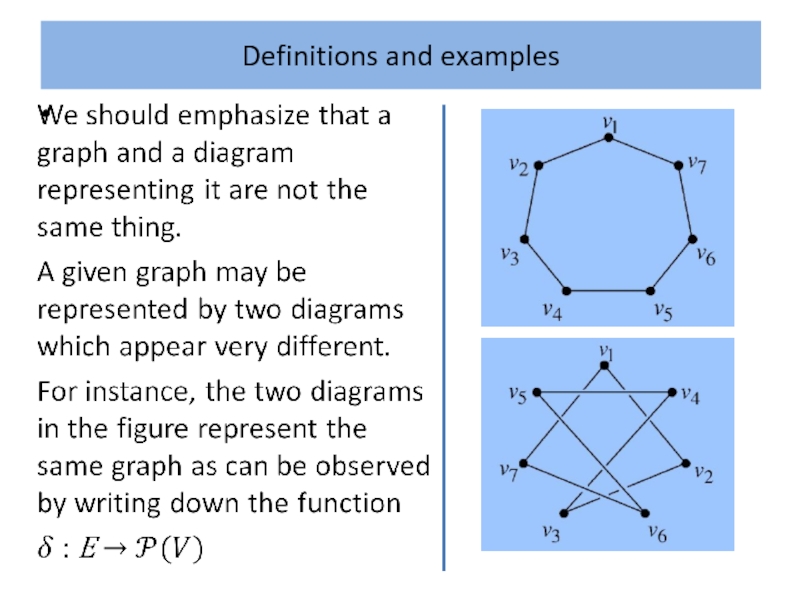
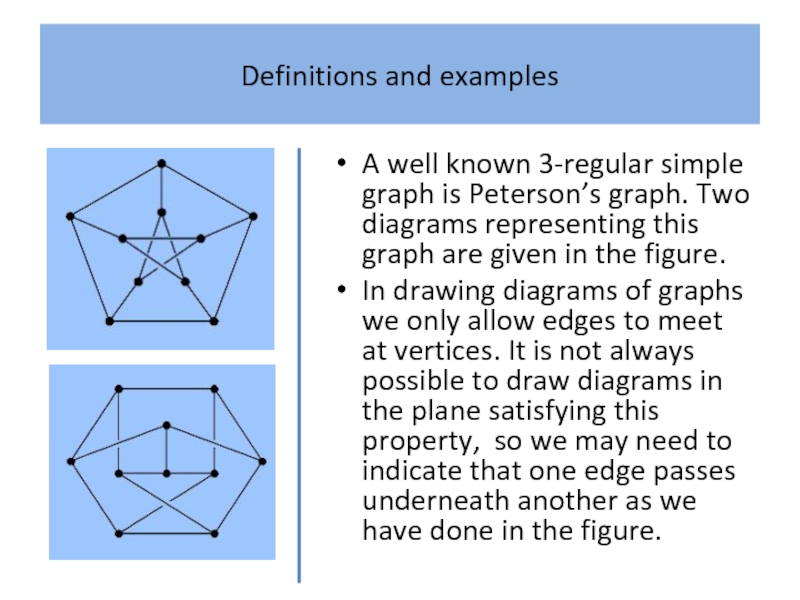
A well known 3-regular simple graph is Peterson’s graph.
Two diagrams representing this graph are given in the figure.
In drawing diagrams of graphs we only allow edges to meet at vertices. It is not always possible to draw diagrams in the plane satisfying this property, so we may need to indicate that one edge passes underneath another as we have done in the figure.
In drawing diagrams of graphs we only allow edges to meet at vertices. It is not always possible to draw diagrams in the plane satisfying this property, so we may need to indicate that one edge passes underneath another as we have done in the figure.
Слайд 18Definitions and examples
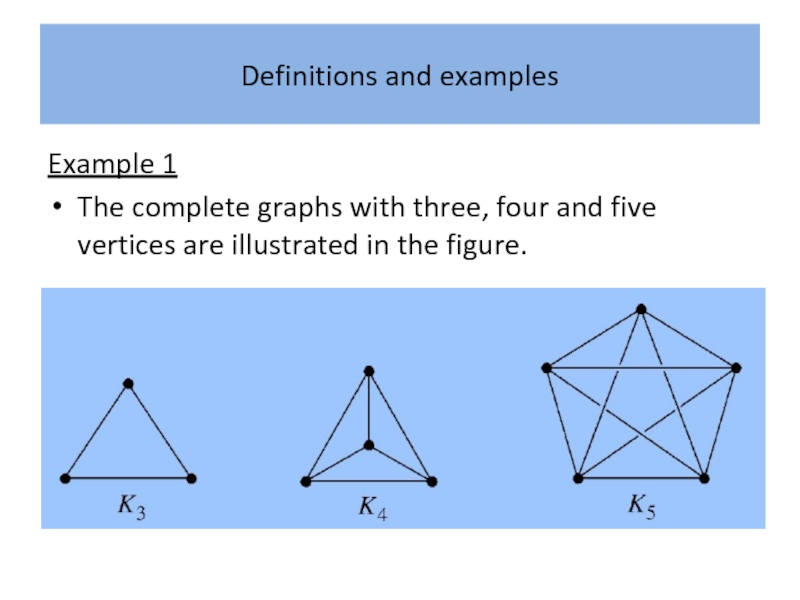
Example 1
Since a complete graph is simple there are
no loops and each pair of distinct vertices is joined by a unique edge. Clearly a complete graph is uniquely specified by the number of its vertices.
Слайд 20Definitions and examples
Example 1
The complete graphs with three, four and five
vertices are illustrated in the figure.
Слайд 32Definitions and examples
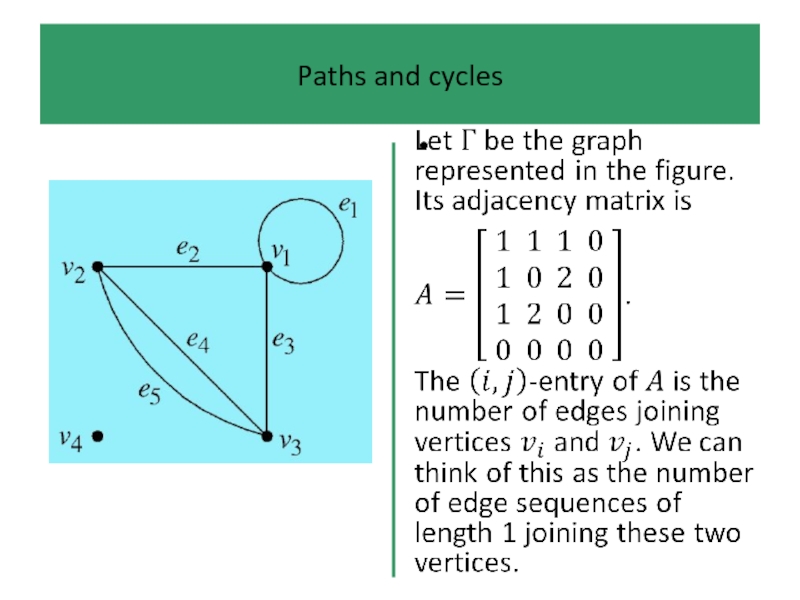
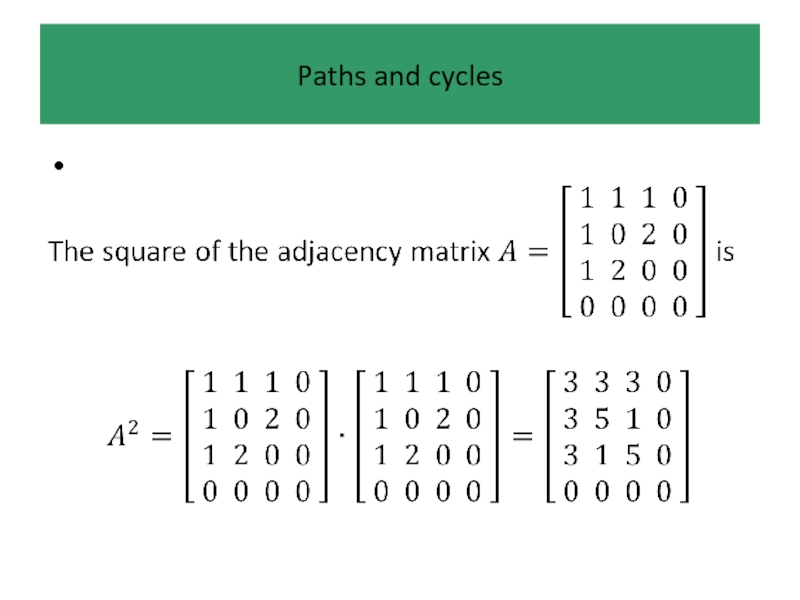
Example 4
A complete graph has adjacency matrix with zeros
along the leading diagonal (since there are no loops) and ones everywhere else (since every vertex is joined to every other by a unique edge).
Слайд 35Paths and cycles
Using the analogy of a road map, we can
consider various types of ‘journeys’ in a graph.
For instance, if the graph actually represents a network of roads connecting various towns, one question we might ask is: is there a journey, beginning and ending at the same town, which visits every other town just once without traversing the same road more than once?
As usual, we begin with some definitions.
For instance, if the graph actually represents a network of roads connecting various towns, one question we might ask is: is there a journey, beginning and ending at the same town, which visits every other town just once without traversing the same road more than once?
As usual, we begin with some definitions.
Слайд 39Paths and cycles
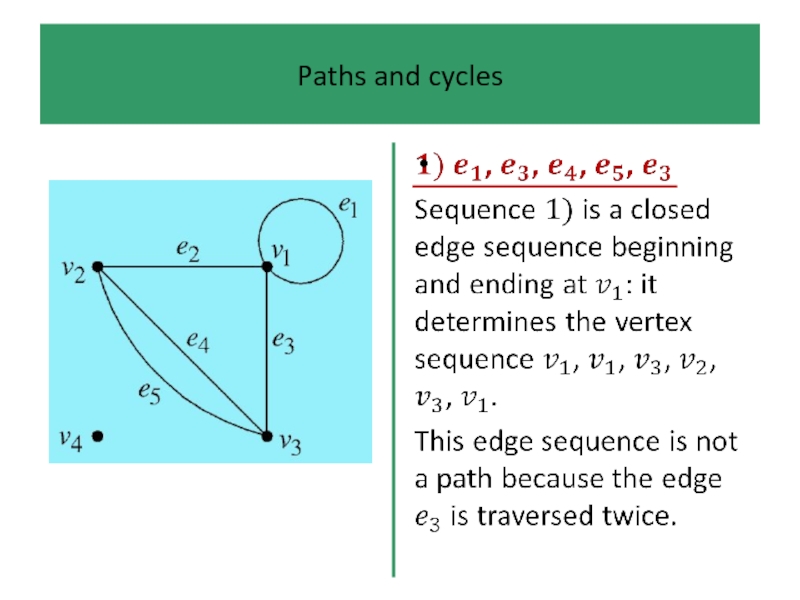
An edge sequence is any finite sequence of edges
which can be traced on the diagram of the graph without removing pen from paper. It may repeat edges, go round loops several times, etc.
Слайд 40Paths and cycles
Edge sequences are too general to be of very
much use which is why we have defined paths.
Слайд 41Paths and cycles
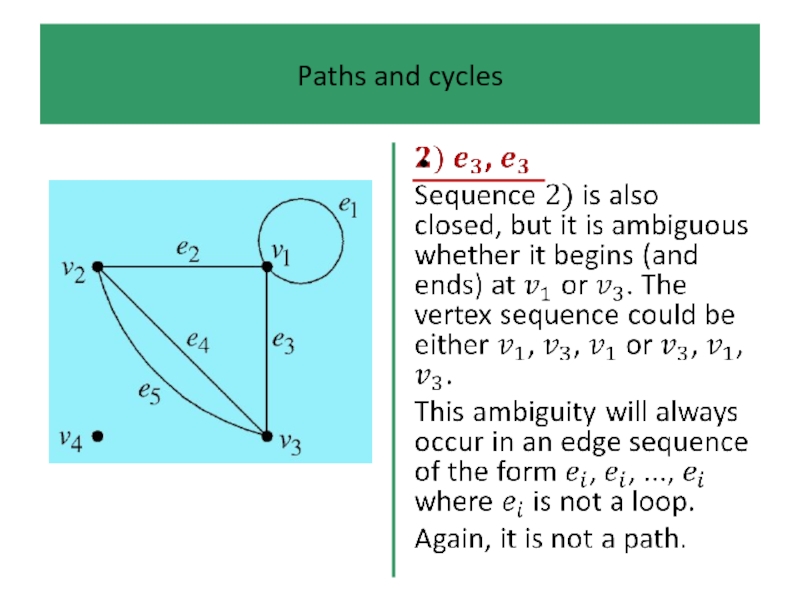
In a path we are not allowed to ‘travel
along’ the same edge more than once.
Слайд 42Paths and cycles
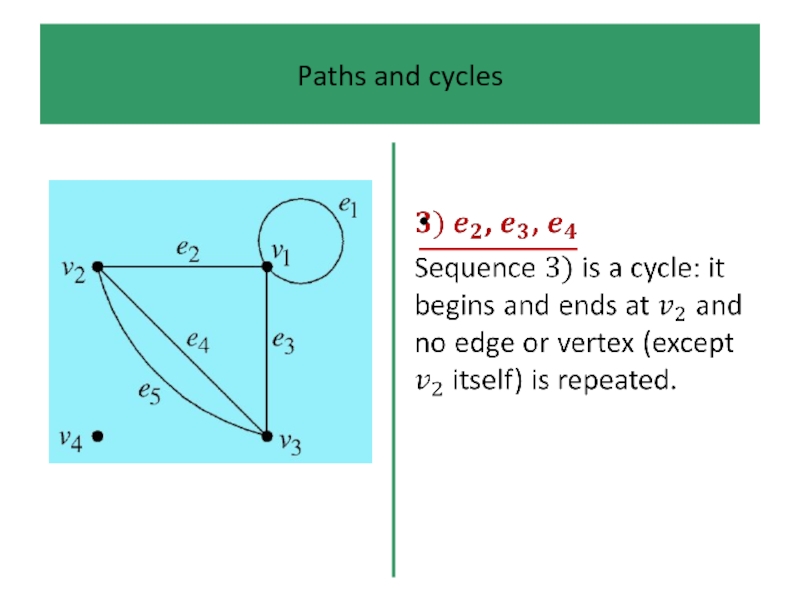
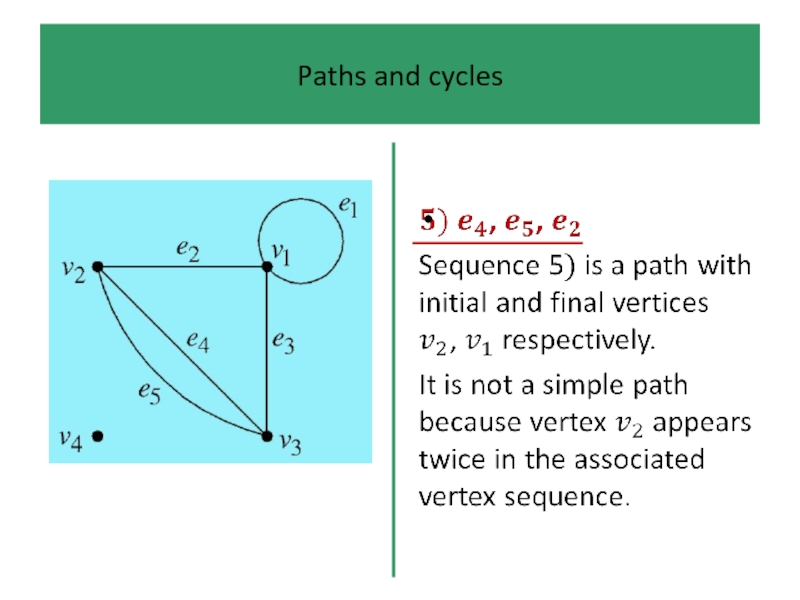
If, in addition, we do not ‘visit’ the same
vertex more than once (which rules out loops), then the path is simple.
Слайд 43Paths and cycles
The edge sequence or path is closed if we
begin and end the ‘journey’ at the same place.
Слайд 59Paths and cycles
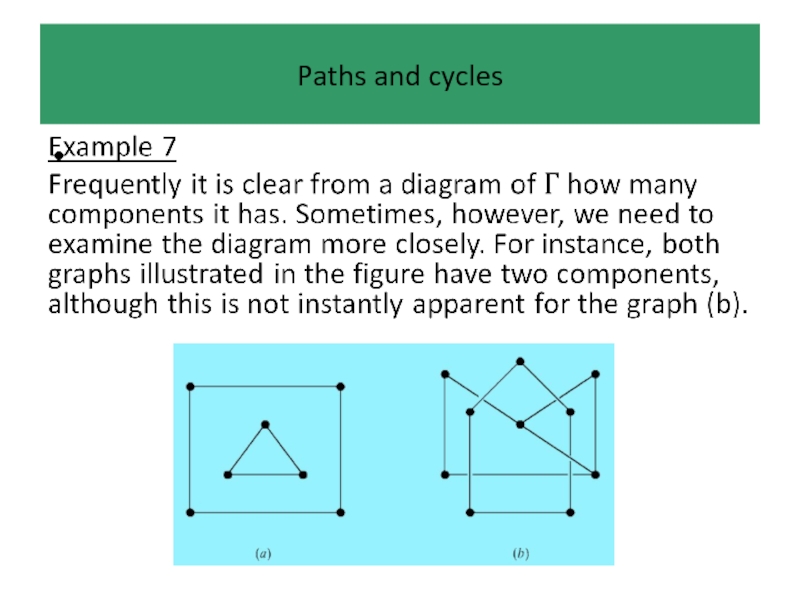
In an intuitively obvious sense, some graphs are ‘all
in one piece’ and others are made up of several pieces.
We can use paths to make this idea more precise.
We can use paths to make this idea more precise.
Слайд 60Paths and cycles
Definition 7
A graph is connected if, given any pair
of distinct vertices, there exists a path connecting them.
Слайд 61Paths and cycles
An arbitrary graph naturally splits up into a number
of connected subgraphs, called its (connected) components.
The components can be defined formally as maximal connected subgraphs.
The components can be defined formally as maximal connected subgraphs.
Слайд 63Paths and cycles
The components of a graph are just its connected
‘pieces’.
In particular, a connected graph has only one component.
Decomposing a graph into its components can be very useful.
It is usually simpler to prove results about connected graphs and properties of arbitrary graphs can frequently then be deduced by considering each component in turn.
In particular, a connected graph has only one component.
Decomposing a graph into its components can be very useful.
It is usually simpler to prove results about connected graphs and properties of arbitrary graphs can frequently then be deduced by considering each component in turn.