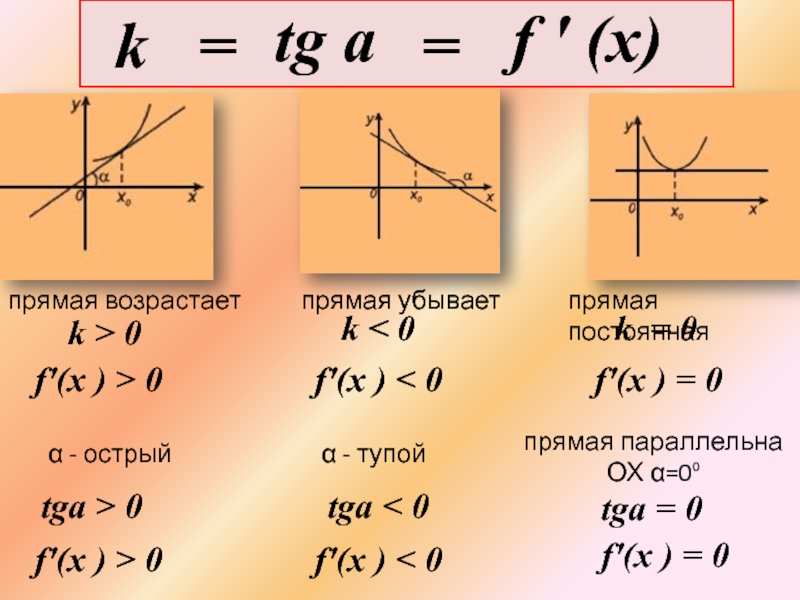Геометрический смысл производной презентация

Содержание

1. Геометрический смысл производной
2. Геометрическая интерпретация производной, впервые данная в конце
3. y=kx k =
4. k =
5. y=f(x) a x y x
6. y=f(x) a x y x
7. f(x+∆х) – f(x) ∆х
8. tga < 0 tga = 0 k
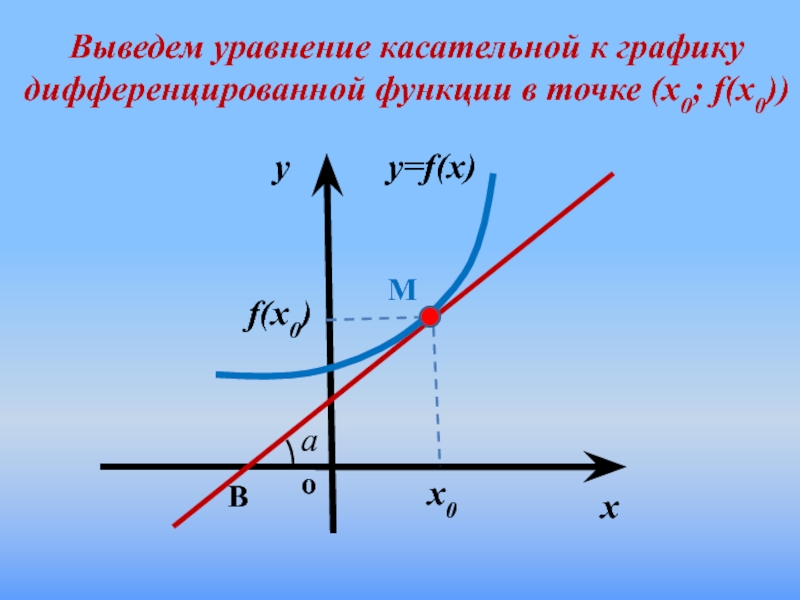
9. Выведем уравнение касательной к графику дифференцированной функции в точке (х0; f(x0))
10. y=kx +b k =
11. Алгоритм нахождения уравнения касательной к
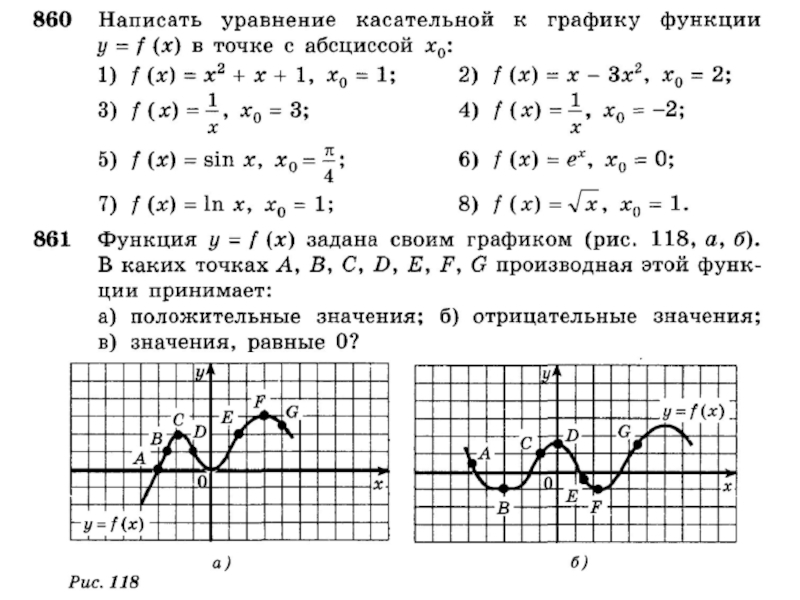
12. Решаем задачи № 857-861 (только нечетные)
14. Домашнее задание № 34 Учебник Алгебра 10-11

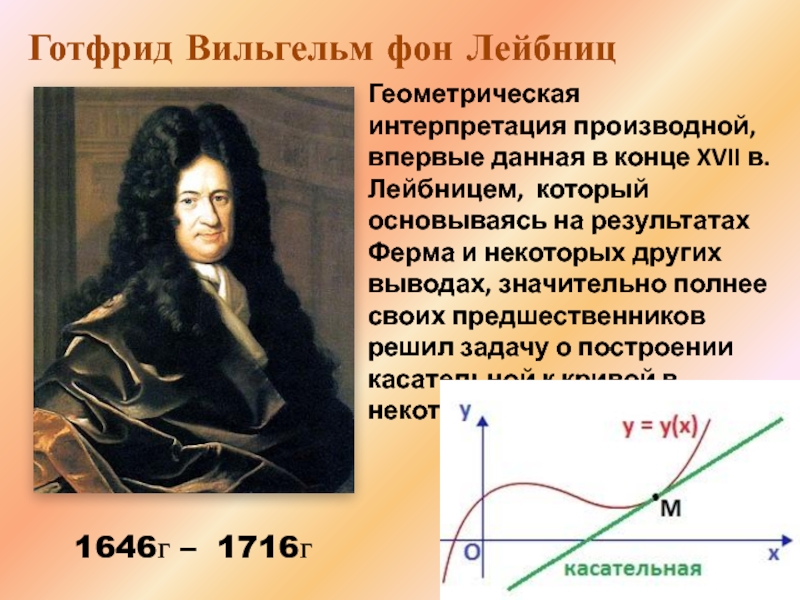
Геометрическая интерпретация производной, впервые данная в конце XVII в. Лейбницем, который основываясь на результатах Ферма и некоторых других выводах, значительно полнее своих предшественников решил задачу о построении касательной к кривой в некоторой

Главная
Математика
Геометрический смысл производной

Слайд 1Геометрический смысл производной
Урок № 34

Слайд 2Геометрическая интерпретация производной, впервые данная в конце XVII в. Лейбницем, который основываясь

на результатах Ферма и некоторых других выводах, значительно полнее своих предшественников решил задачу о построении касательной к кривой в некоторой точке.

1646г – 1716г

Готфрид Вильгельм фон Лейбниц

Слайд 3y=kx
k =

противолежащий катет

прилежащий катет

tg a

y=kx+b

Слайд 4
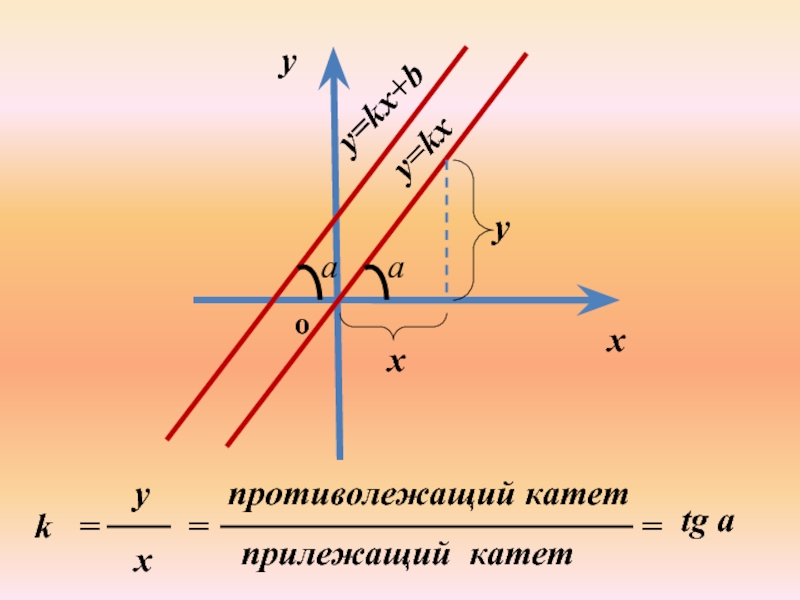
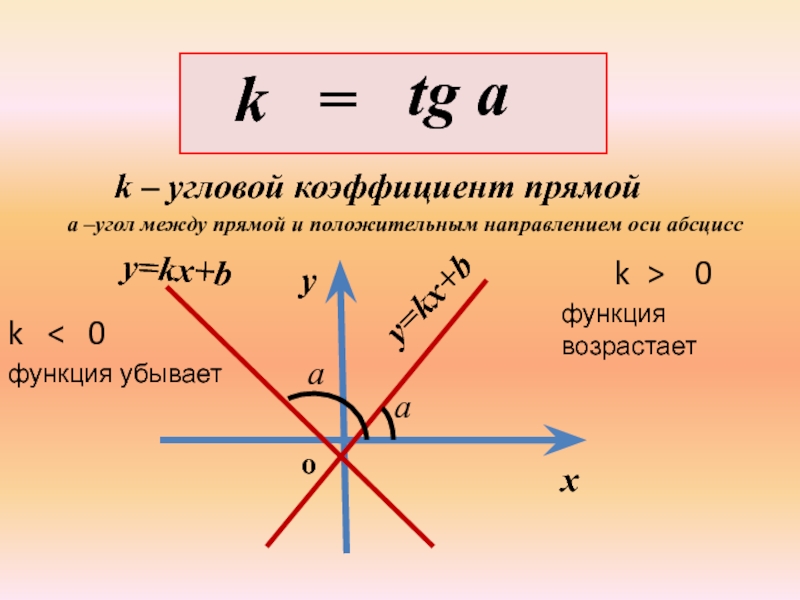
k =

tg a

k – угловой коэффициент прямой

а –угол между прямой и положительным направлением оси абсцисс

y=kx+b

k 0

функция возрастает

функция убывает

Слайд 5y=f(x)
a
x

y
x

M
B
C
A
x+∆х
f(x)
f(x+∆х)

f(x+∆х) – f(x)
∆х
k = tg

MAC =

f(x+∆х) – f(x)

∆х

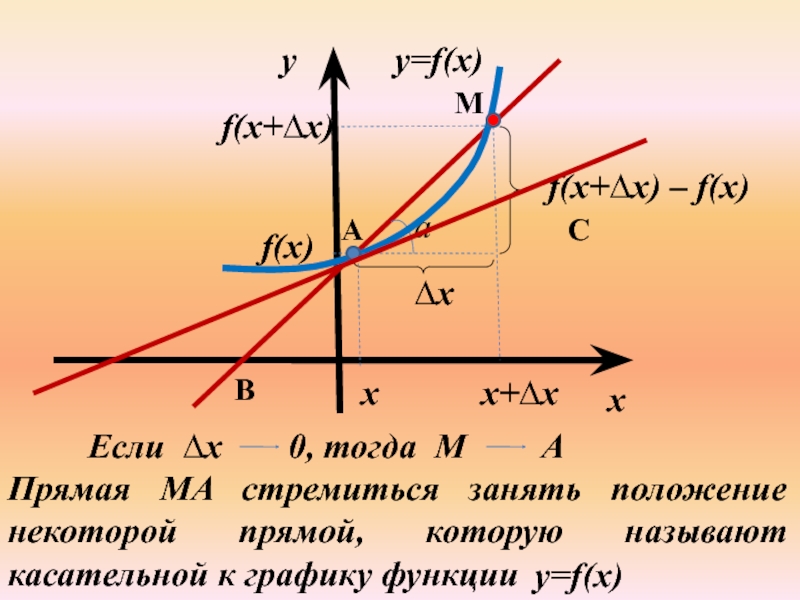
Слайд 6y=f(x)
a
x

y
x

M
B
C
A
x+∆х
f(x)
f(x+∆х)

f(x+∆х) – f(x)
∆х
Если ∆х
0, тогда М
А
Прямая MA стремиться занять

положение некоторой прямой, которую называют касательной к графику функции

y=f(x)

Слайд 7
f(x+∆х) – f(x)
∆х
=
lim k =
f ' (x)
k

tg a

f ' (x)

∆х

Значение производной в точке равно
угловому коэффициенту касательной к графику функции в этой точке

lim

∆х

Слайд 8tga < 0
tga = 0
k > 0
f'(x ) > 0
f'(x )

< 0

f'(x ) = 0

прямая возрастает

прямая убывает

прямая параллельна ОХ α=0⁰

прямая постоянная

k < 0

k = 0

tga > 0

k =

tg a

f ' (x)

f'(x ) = 0

α - острый

α - тупой

f'(x ) > 0

f'(x ) < 0

Слайд 9Выведем уравнение касательной к графику дифференцированной функции в точке (х0; f(x0))

Слайд 10

y=kx +b
k =

tg a

f ' (x)

y=f' (x0 )x+ b

Т.к. касательная проходит через точку с координатами
(х0; f(x0)) , подставим ее координаты в уравнение (2) и найдем b

(1)

(2)

f(x0)=f' (x0 )x0+ b

b =f(x0) – f' (x0 )x0

Подставьте в уравнение (2) значение b и сделав соответствующие преобразования получите:

у = f(x0) + f '(x0)(х – х0)

Слайд 11Алгоритм
нахождения уравнения касательной
к графику функции y=f(x)
в точке с

абсциссой х0

f(x0) – находим значение функции в данной точке
f '(x) – находим производную данной функции
f'(x0) - находим значение производной функции в данной точке
Подставляем данные в уравнение касательной к графику функции

у = f(x0) + f '(x0)(х – х0)

Слайд 12Решаем задачи № 857-861 (только нечетные)

Слайд 13

Слайд 14Домашнее задание № 34
Учебник Алгебра 10-11 кл. Алимов
§ 48, стр. 251-255,
№

857-861 (только четные).

Скачать презентацию

Геометрический смысл производной презентация

Содержание

Слайд 1Геометрический смысл производной
Урок № 34

Слайд 2Геометрическая интерпретация производной, впервые данная в конце XVII в. Лейбницем, который основываясь

Слайд 3y=kx
k =

Слайд 4
k =

Слайд 5y=f(x)
a
x

y
x

M
B
C
A
x+∆х
f(x)
f(x+∆х)

f(x+∆х) – f(x)
∆х
k = tg

Слайд 6y=f(x)
a
x

y
x

M
B
C
A
x+∆х
f(x)
f(x+∆х)

f(x+∆х) – f(x)
∆х
Если ∆х
0, тогда М
А
Прямая MA стремиться занять

Слайд 7
f(x+∆х) – f(x)
∆х
=
lim k =
f ' (x)
k

Слайд 8tga < 0
tga = 0
k > 0
f'(x ) > 0
f'(x )

Слайд 9Выведем уравнение касательной к графику дифференцированной функции в точке (х0; f(x0))

Слайд 10

y=kx +b
k =

Слайд 11Алгоритм
нахождения уравнения касательной
к графику функции y=f(x)
в точке с

Слайд 12Решаем задачи № 857-861 (только нечетные)

Слайд 13

Слайд 14Домашнее задание № 34
Учебник Алгебра 10-11 кл. Алимов
§ 48, стр. 251-255,
№

Обратная связь

Что такое ThePresentation.ru?

Геометрический смысл производной презентация

Содержание

Слайд 1Геометрический смысл производнойУрок № 34

Слайд 2Геометрическая интерпретация производной, впервые данная в конце XVII в. Лейбницем, который основываясь

Слайд 3y=kxk =

Слайд 4k =

Слайд 5y=f(x)axyxMBCAx+∆хf(x)f(x+∆х)f(x+∆х) – f(x)∆х k = tg

Слайд 6y=f(x)axyxMBCAx+∆хf(x)f(x+∆х)f(x+∆х) – f(x)∆хЕсли ∆х 0, тогда М АПрямая MA стремиться занять

Слайд 7f(x+∆х) – f(x)∆х =lim k = f ' (x)k

Слайд 8tga < 0tga = 0k > 0f'(x ) > 0f'(x )

Слайд 9Выведем уравнение касательной к графику дифференцированной функции в точке (х0; f(x0))

Слайд 10y=kx +bk =

Слайд 11Алгоритм нахождения уравнения касательной к графику функции y=f(x) в точке с

Слайд 12Решаем задачи № 857-861 (только нечетные)

Слайд 13

Слайд 14Домашнее задание № 34Учебник Алгебра 10-11 кл. Алимов§ 48, стр. 251-255,№

Похожие презентации

Обратная связь

Что такое ThePresentation.ru?

Слайд 1Геометрический смысл производной
Урок № 34

Слайд 3y=kx
k =

Слайд 4
k =

Слайд 5y=f(x)
a
x

y
x

M
B
C
A
x+∆х
f(x)
f(x+∆х)

f(x+∆х) – f(x)
∆х
k = tg

Слайд 6y=f(x)
a
x

y
x

M
B
C
A
x+∆х
f(x)
f(x+∆х)

f(x+∆х) – f(x)
∆х
Если ∆х
0, тогда М
А
Прямая MA стремиться занять

Слайд 7
f(x+∆х) – f(x)
∆х
=
lim k =
f ' (x)
k

Слайд 8tga < 0
tga = 0
k > 0
f'(x ) > 0
f'(x )

Слайд 10

y=kx +b
k =

Слайд 11Алгоритм
нахождения уравнения касательной
к графику функции y=f(x)
в точке с

Слайд 14Домашнее задание № 34
Учебник Алгебра 10-11 кл. Алимов
§ 48, стр. 251-255,
№