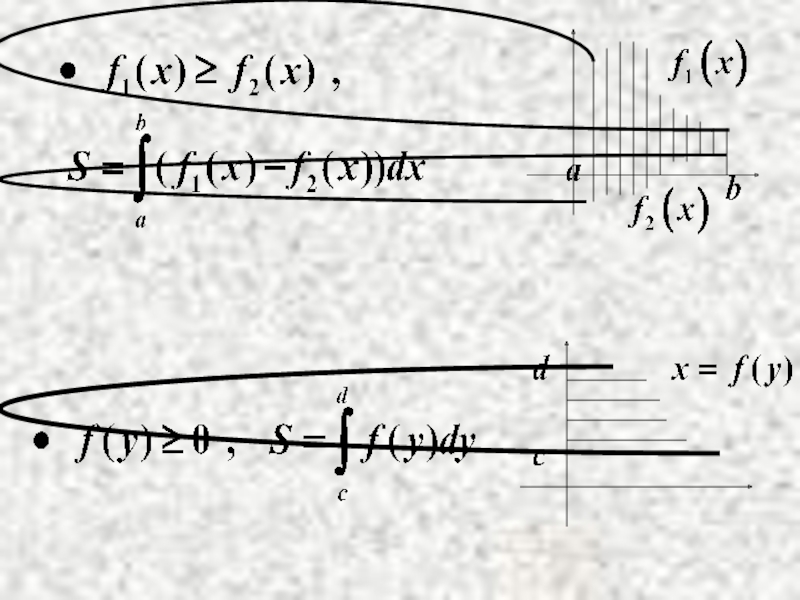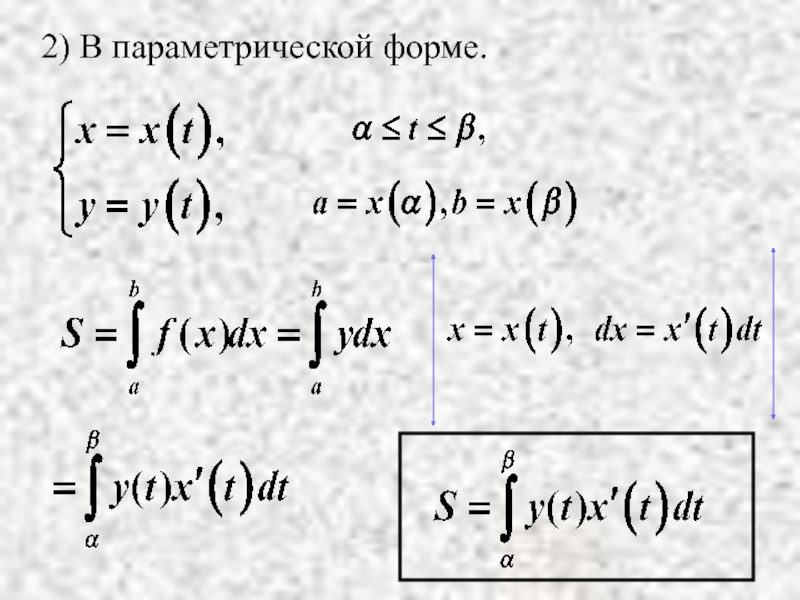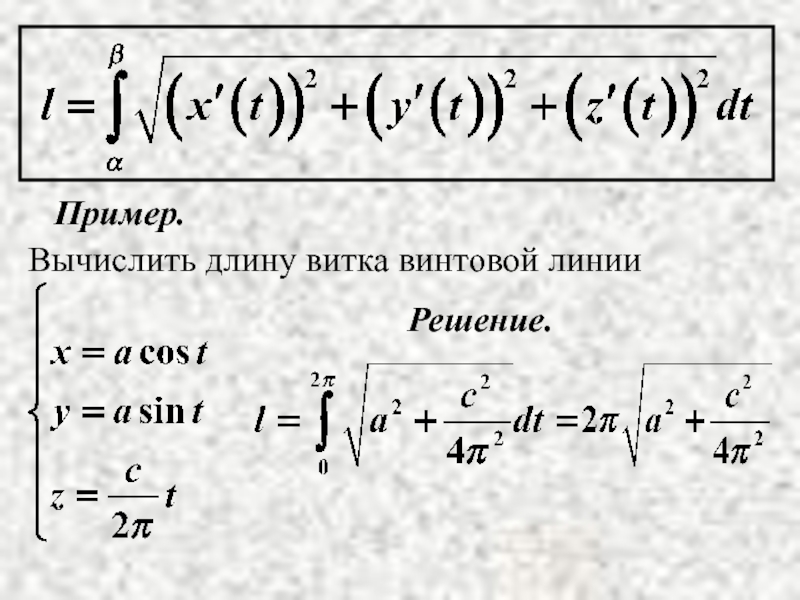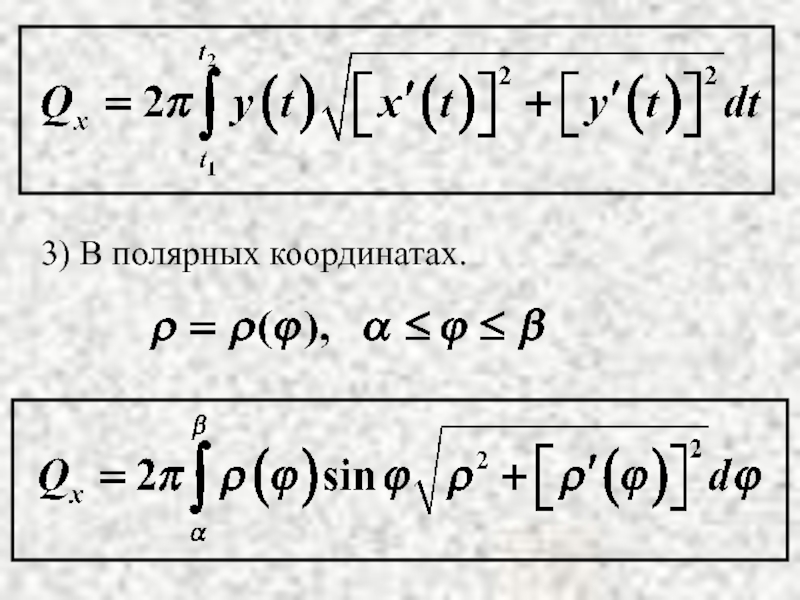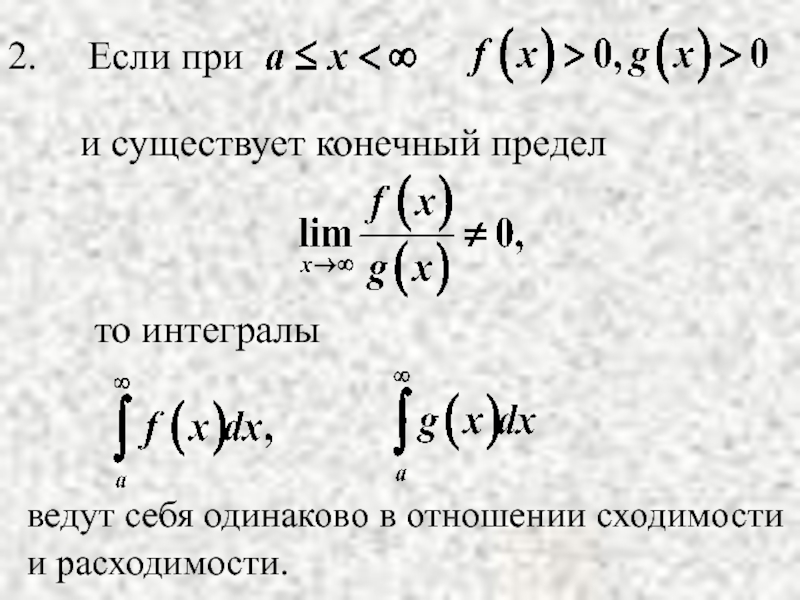- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геометрические приложения определенного интеграла презентация
Содержание
- 1. Геометрические приложения определенного интеграла
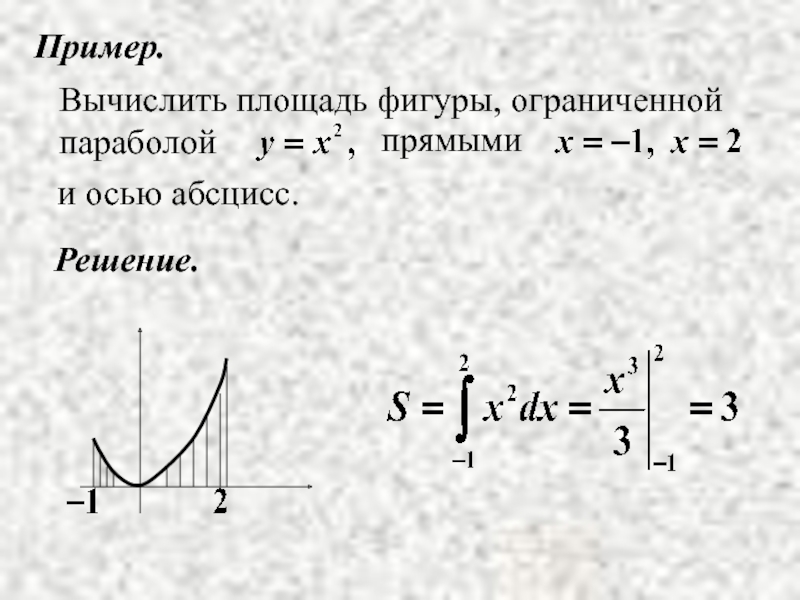
- 3. Пример. Решение.
- 4. 2) В параметрической форме.
- 5. Вычислить площадь эллипса. Пример. Решение. Уравнения эллипса в параметрической форме:
- 6. 3) В полярных координатах.
- 7. Пример. Решение.
- 8. 1) В декартовых координатах. 2) В параметрической форме.
- 9. Пример. Вычислить длину витка винтовой линии Решение.
- 10. 3) В полярных координатах. Пример. Решение.
- 11. 1) В декартовых координатах. 2) В параметрической форме.
- 12. 3) В полярных координатах.
- 14. Пример. Решение. Основание треугольника
- 16. 2) Вычисление объёмов тел вращения.
- 17. Пример. Решение.
- 18. Несобственные интегралы. называется несобственным интегралом
- 19. Если предел существует
- 20. Обобщённая формула Ньютона-Лейбница. Точно также,
- 21. Вычислить несобственные интегралы, или доказать
- 22. Признаки сходимости интегралов с бесконечными пределами. Признаки сравнения
- 23. то интегралы ведут себя одинаково
- 24. расходится Пример. Исследовать на сходимость Решение.
- 25. Несобственные интегралы второго рода. называется
- 26. Если предел существует и конечен,
- 27. Если каждый из интегралов в правой
- 28. Пример. Решение. По обобщенной формуле Ньютона-Лейбница:
- 29. Признаки сходимости несобственных интегралов от неограниченных функций
Слайд 13 - площадь любого сечения
Вычисление объёмов по заданным площадям
поперечных сечений.
Объём тела
Слайд 19
Если предел существует и конечен, то несобственный интеграл называется
Если предел не существует, или бесконечен, то несобственный интеграл называется расходящимся.
Слайд 21 Вычислить несобственные интегралы, или
доказать что они расходятся.
(сходится)
Пример.
(расходится)
(предел
Слайд 23то интегралы
ведут себя одинаково в отношении сходимости
и
и существует конечный предел
Слайд 26
Если предел существует и конечен, то несобственный интеграл называется сходящимся.
Если предел не существует, или бесконечен, то несобственный интеграл называется расходящимся.
Слайд 27
Если каждый из интегралов в правой части равенства сходится, то несобственный
В противном случае – расходящимся.