- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Функция ұғымы және оның берілу тәсілдері презентация
Содержание
- 1. Функция ұғымы және оның берілу тәсілдері
- 2. ФУНКЦИЯ ҰҒЫМЫ ЖӘНЕ ОНЫҢ БЕРІЛУ ТӘСІЛДЕРІ
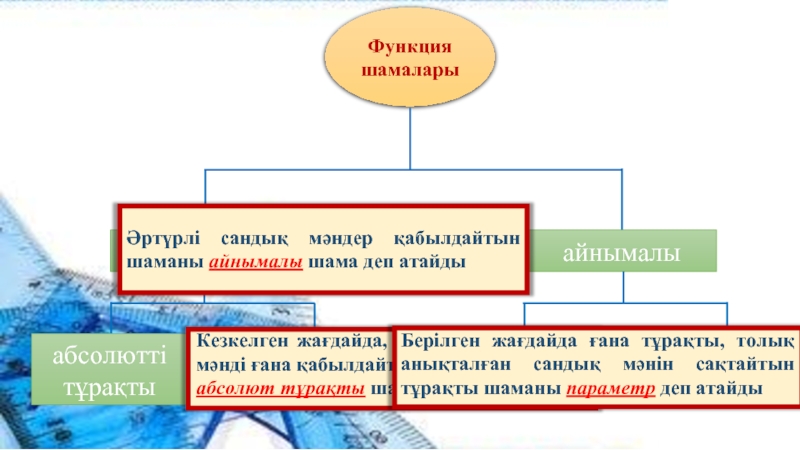
- 3. Функция шамалары тұрақты айнымалы абсолютті тұрақты параметр тәуелді тәуелсіз
- 4. маятниктің тербеліс периодының формуласы π және
- 5. Берілген функцияның шамаларын ажыратып жазыңыз
- 6. Жеңіл машинаның 60 км/сағ. жылдамдықпен жүріп өткен
- 7. Жұмысшының 10 күнде істеген жұмысының көлемі оның
- 8. Дөңгелектің ауданы оның радиусына тәуелді. r
- 9. Тәуелді және тәуелсіз айнымалы шамалары арасындағы
- 10. Анықтама. Тәуелсіз айнымалы x-тің әрбір мәніне тәуелді
- 11. Берілген суреттердің қайсысы функция болады
- 12. Анықтама. f(x) функциясы белгілі бір мән қабылдайтын
- 13. Функцияның анықталу облысын табу: егер функция әртүрлі
- 14. Функцияның анықталу облысын және мәндер жиынын
Слайд 1АЛГЕБРА ЖӘНЕ
АНАЛИЗ БАСТАМАЛАРЫ
10
Жұмашев Жансейіт Қарасайұлы
Математика пәнінің
Слайд 4маятниктің тербеліс периодының формуласы
π және 2 сандары – абсолют тұрақтылар
g
l – тәуелсіз айнымалы
T – тәуелді айнымалы
Слайд 5
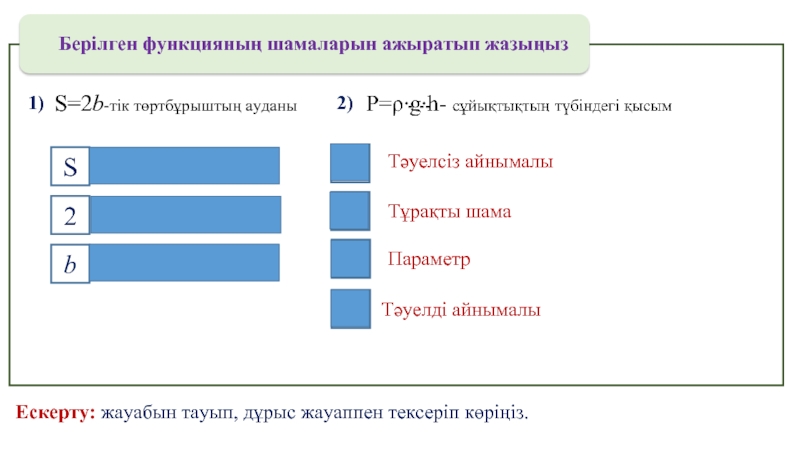
Берілген функцияның шамаларын ажыратып жазыңыз
1)
S
Тәуелді айнымалы
2
Тұрақты шама
b
Тәуелсіз айнымалы
2)
h
ρ
g
P
Тәуелді айнымалы
Тұрақты шама
Тәуелсіз айнымалы
Параметр
S=2b-тік төртбұрыштың ауданы
Ескерту: жауабын тауып, дұрыс жауаппен тексеріп көріңіз.
Слайд 6Жеңіл машинаның 60 км/сағ. жылдамдықпен жүріп өткен жол қозғалу уақытына тәуелді
60 км/сағ
t – қозғалысының уақыты
S – жүрген жолын
S=60t – t сағатта жүрген жол
t – тәуелсіз айнымалы
S – тәуелді айнымалы
60 – абсолютті тұрақты
Слайд 7Жұмысшының 10 күнде істеген жұмысының көлемі оның іс өнімділігіне тәуелді.
V
a – іс өнімділігін
сонда ол 10 күнде көлемі V=10a – ға тең жұмыс істейді
а – тәуелсіз айнымалы
V – тәуелді айнымалы
10 – абсолютті тұрақты
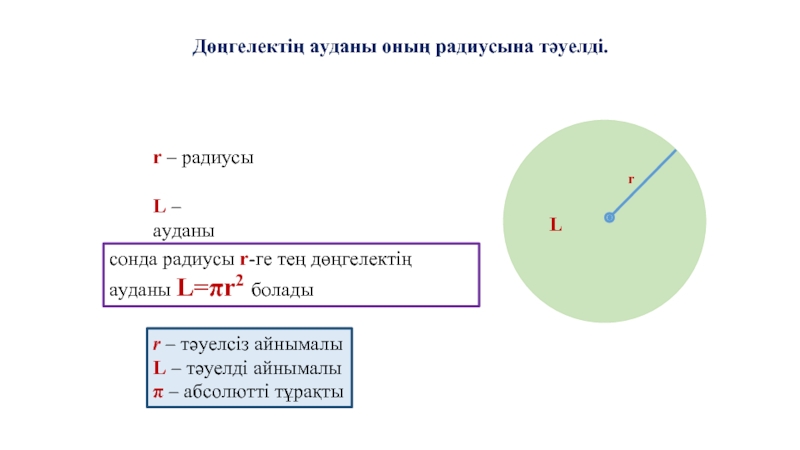
Слайд 8Дөңгелектің ауданы оның радиусына тәуелді.
r – радиусы
L – ауданы
сонда радиусы
L
r
r – тәуелсіз айнымалы
L – тәуелді айнымалы
π – абсолютті тұрақты
Слайд 9
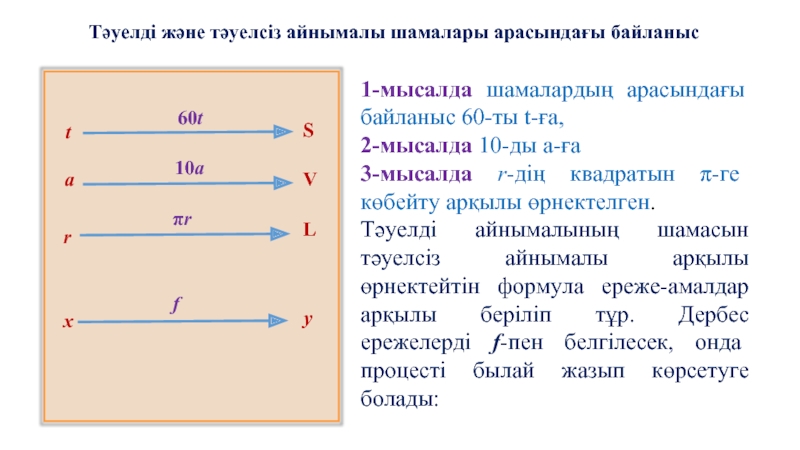
Тәуелді және тәуелсіз айнымалы шамалары арасындағы байланыс
t
S
60t
a
V
10a
r
L
πr
x
y
f
1-мысалда шамалардың арасындағы байланыс 60-ты
2-мысалда 10-ды а-ға
3-мысалда r-дің квадратын π-ге көбейту арқылы өрнектелген.
Тәуелді айнымалының шамасын тәуелсіз айнымалы арқылы өрнектейтін формула ереже-амалдар арқылы беріліп тұр. Дербес ережелерді f-пен белгілесек, онда процесті былай жазып көрсетуге болады:
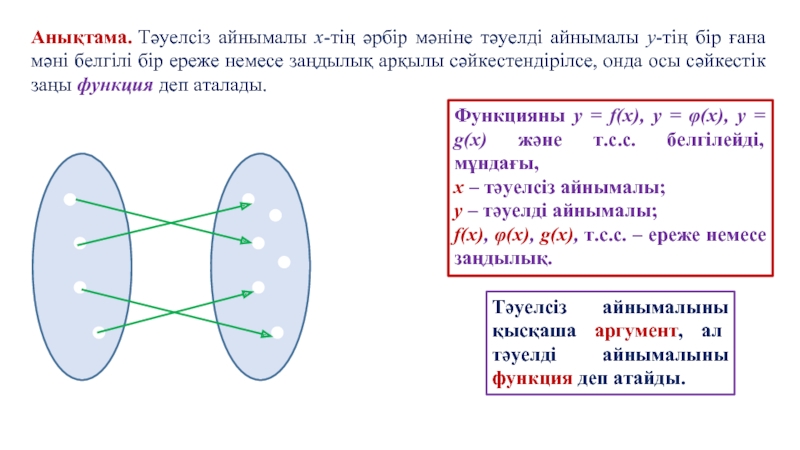
Слайд 10Анықтама. Тәуелсіз айнымалы x-тің әрбір мәніне тәуелді айнымалы y-тің бір ғана
Функцияны y = f(x), y = φ(x), y = g(x) және т.с.с. белгілейді, мұндағы,
x – тәуелсіз айнымалы;
y – тәуелді айнымалы;
f(x), φ(x), g(x), т.с.с. – ереже немесе заңдылық.
Тәуелсіз айнымалыны қысқаша аргумент, ал тәуелді айнымалыны функция деп атайды.
Слайд 11
Берілген суреттердің қайсысы функция болады немесе болмайтындығын анықтаңыз?
а) және б) –
Слайд 12Анықтама. f(x) функциясы белгілі бір мән қабылдайтын тәуелсіз айнымалының нақты мәндер
Функцияның D(f) анықталу облысын;
х пен у мәндері арасындағы ереже немесе заңдылықты;
функцияның Е(f) мәндер жиынын.
функциясы көпмүше болғандықтан, аргументтің кез келген мәнінде анықталған. Демек, функцияның анықталу облысы барлық нақты сандар жиыны, яғни
D(у) = R;
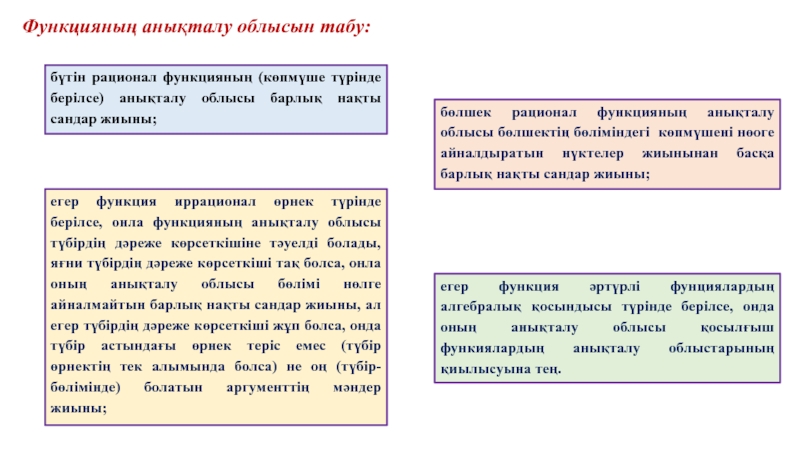
Слайд 13Функцияның анықталу облысын табу:
егер функция әртүрлі фунциялардың алгебралық қосындысы түрінде берілсе,
бүтін рационал функцияның (көпмүше түрінде берілсе) анықталу облысы барлық нақты сандар жиыны;
бөлшек рационал функцияның анықталу облысы бөлшектің бөліміндегі көпмүшені нөоге айналдыратын нүктелер жиынынан басқа барлық нақты сандар жиыны;
егер функция иррационал өрнек түрінде берілсе, онла функцияның анықталу облысы түбірдің дәреже көрсеткішіне тәуелді болады, яғни түбірдің дәреже көрсеткіші тақ болса, онла оның анықталу облысы бөлімі нөлге айналмайтын барлық нақты сандар жиыны, ал егер түбірдің дәреже көрсеткіші жұп болса, онда түбір астындағы өрнек теріс емес (түбір өрнектің тек алымында болса) не оң (түбір-бөлімінде) болатын аргументтің мәндер жиыны;
Слайд 14
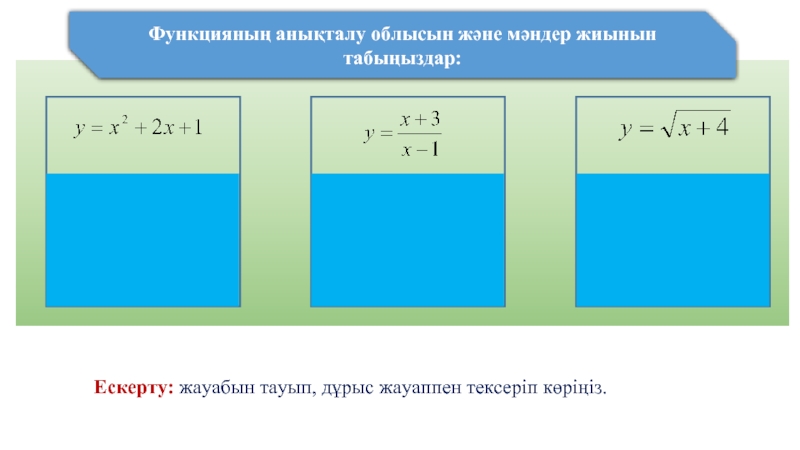
Функцияның анықталу облысын және мәндер жиынын табыңыздар:
D(y)=R
E(y) =R
D(y)=(-∞; 1)U(1;+∞)
E(y)=(-∞; 1)U(1;+∞)
D(y)=[-4;+∞)
E(y) =(0
Ескерту: жауабын тауып, дұрыс жауаппен тексеріп көріңіз.