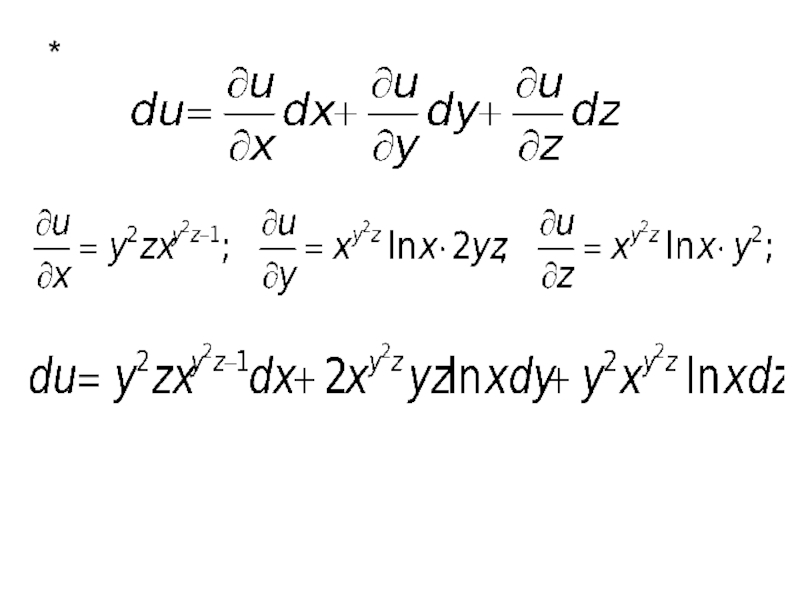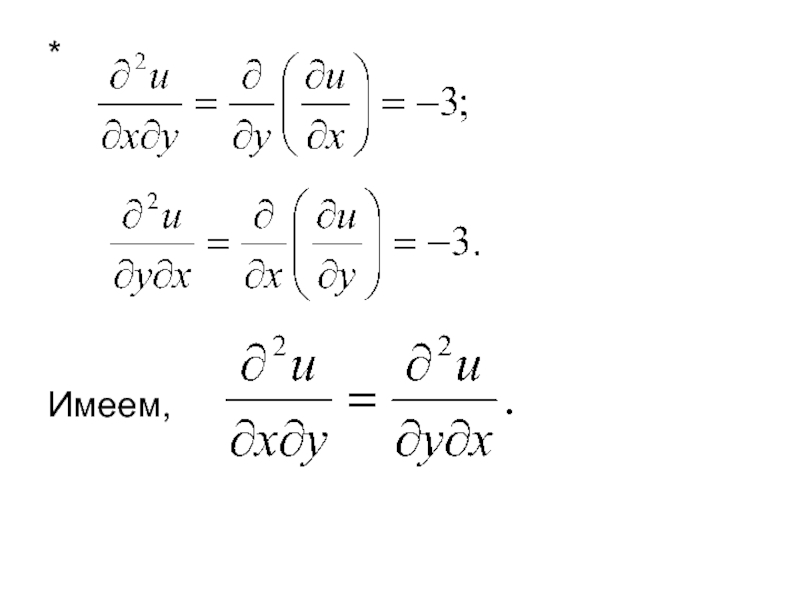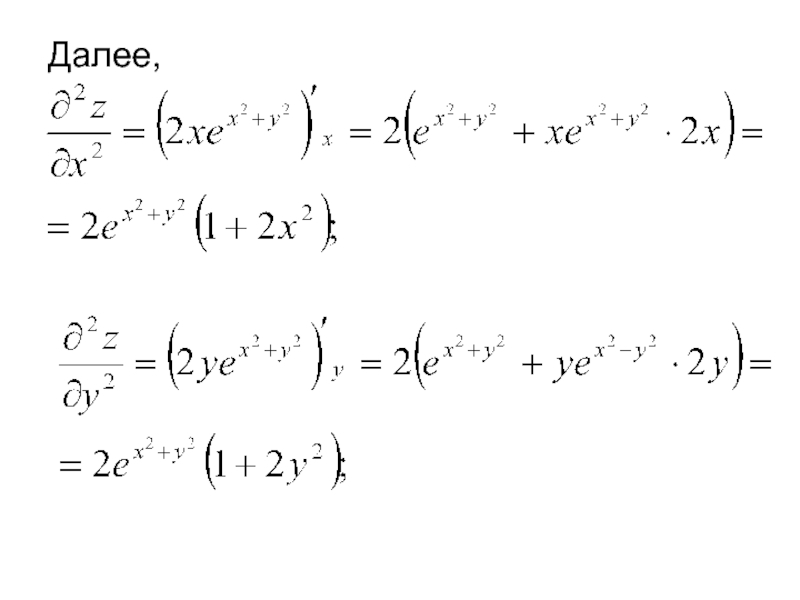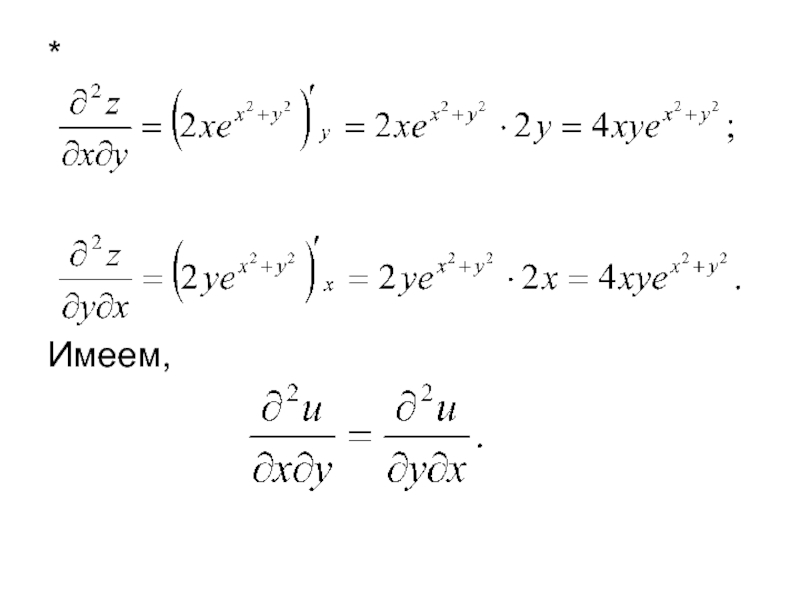- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Функция нескольких переменных презентация
Содержание
- 1. Функция нескольких переменных
- 2. Вопросы Понятие функции двух и более переменных.
- 3. 1. Рассмотрим функцию двух переменных.
- 4. Опр. Областью определения функции z называется
- 5. Опр. Число А называется пределом функции
- 6. Опр. Пусть точка М0(х0, у0) принадлежит
- 7. Если в какой – либо точке
- 8. 2. Дифференцирование функции нескольких переменных Опр.
- 9. Можно записать
- 10. Обозначение: Аналогично определяется частная производная функции по у:
- 11. Полное приращение и полный дифференциал Опр.
- 12. где α1 и α2 – бесконечно
- 13. Для функции произвольного числа переменных:
- 14. *
- 15. Пример 2. Найти полный дифференциал функции
- 16. Получаем Частные производные
- 17. Будем называть эти производные частными производными
- 18. Продолжая дифференцировать полученные равенства, получим частные
- 19. Теорема. Если функция f(x, y) и
- 31. *Пример 4. Найти экстремум функции
Вопросы Понятие функции двух и более переменных. Дифференцирование функции нескольких переменных. Частные производные. Полный дифференциал. Экстремум функции двух переменных.
Слайд 2Вопросы
Понятие функции двух и более переменных.
Дифференцирование функции нескольких переменных.
Частные производные. Полный
дифференциал.
Экстремум функции двух переменных.
Экстремум функции двух переменных.
Слайд 3
1. Рассмотрим функцию двух переменных.
Опр. Если каждой паре независимых друг
от друга чисел (х, у) из некоторого множества по какому - либо правилу ставится в соответствие одно значение переменной z, то она называется функцией двух переменных.
z = f(x, y)
z = f(x, y)
Слайд 4
Опр. Областью определения функции z называется совокупность пар (х, у), при
которых функция z существует.
Опр. Окрестностью точки М0(х0, у0) радиуса r называется совокупность всех точек (х, у), которые удовлетворяют условию
.
Опр. Окрестностью точки М0(х0, у0) радиуса r называется совокупность всех точек (х, у), которые удовлетворяют условию
.
Слайд 5
Опр. Число А называется пределом функции f(x, y) при стремлении точки
М(х, у) к точке М0(х0, у0), если для любого числа ε > 0 найдется такое число r > 0, что для любой точки М(х, у), для которых верно условие
также верно и условие
Записывают:
также верно и условие
Записывают:
Слайд 6
Опр. Пусть точка М0(х0, у0) принадлежит области определения функции f(x, y).
Тогда функция z = f(x, y) называется непрерывной в точке М0(х0, у0), если
(1)
причем точка М(х, у) стремится к точке М0(х0, у0) произвольным образом.
(1)
причем точка М(х, у) стремится к точке М0(х0, у0) произвольным образом.
Слайд 7
Если в какой – либо точке условие (1) не выполняется, то
эта точка называется точкой разрыва функции f(x, y). Это может быть в следующих случаях:
1. Функция z = f(x, y) не определена в точке М0(х0, у0).
2. Не существует предел в точке
М0(х0, у0).
3. Этот предел существует, но он не равен f( x0, y0).
1. Функция z = f(x, y) не определена в точке М0(х0, у0).
2. Не существует предел в точке
М0(х0, у0).
3. Этот предел существует, но он не равен f( x0, y0).
Слайд 8
2. Дифференцирование функции
нескольких переменных
Опр. Пусть в некоторой области задана функция z
= f(x, y). Возьмем произвольную точку М(х, у) и дадим приращение Δх переменной х. Тогда величина Δzx = f( x + Δx, y) – f(x, y) называется частным приращением функции по х.
Слайд 11
Полное приращение и полный дифференциал
Опр. Для функции f(x, y) выражение
Δz
= f( x + Δx, y + Δy) – f(x, y)
называется полным приращением.
Полное приращение функции f(x, y) в некоторой точке (х, у), можно представить как
называется полным приращением.
Полное приращение функции f(x, y) в некоторой точке (х, у), можно представить как
Слайд 12
где α1 и α2 – бесконечно малые функции при Δх →
0 и Δу → 0 соответственно.
Опр. Полным дифференциалом функции z = f(x, y) называется главная линейная относительно Δх и Δу часть приращения функции Δz в точке (х, у).
Опр. Полным дифференциалом функции z = f(x, y) называется главная линейная относительно Δх и Δу часть приращения функции Δz в точке (х, у).
Слайд 16
Получаем
Частные производные высших порядков
Если функция f(x, y) определена в некоторой области
D, то ее частные производные
тоже будут определены в той же области или ее части.
тоже будут определены в той же области или ее части.
Слайд 17
Будем называть эти производные частными производными первого порядка.
Производные этих функций будут
частными производными второго порядка.
Слайд 18
Продолжая дифференцировать полученные равенства, получим частные производные более высоких порядков.
Опр. Частные
производные вида
и т.д. называются смешанными производными.
и т.д. называются смешанными производными.
Слайд 19
Теорема. Если функция f(x, y) и ее частные производные определены
и непрерывны в точке М(х, у) и ее окрестности, то верно соотношение:
т.е. частные производные высших порядков не зависят от порядка дифференцирования.
т.е. частные производные высших порядков не зависят от порядка дифференцирования.
Слайд 31
*Пример 4. Найти экстремум функции
Решение. Найдем частные производные первого порядка:
Используя необходимые
условия экстремума, находим стационарные точки:
