- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Функции. Определение функции презентация
Содержание
- 1. Функции. Определение функции
- 2. 1.Определение функции Пусть заданы множества Х и
- 3. f ОБЛАСТЬ ОПРЕДЕЛЕНИЯ МНОЖЕСТВО
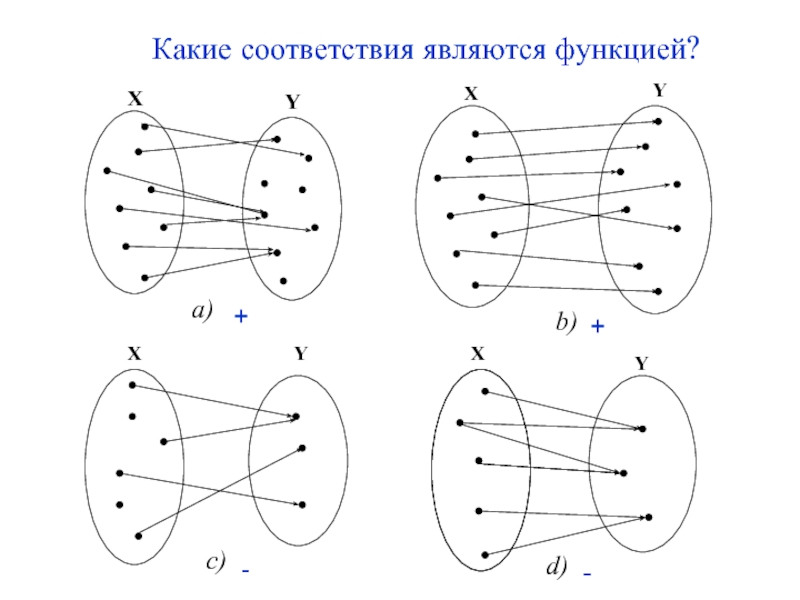
- 4. Какие соответствия являются функцией? + + - -
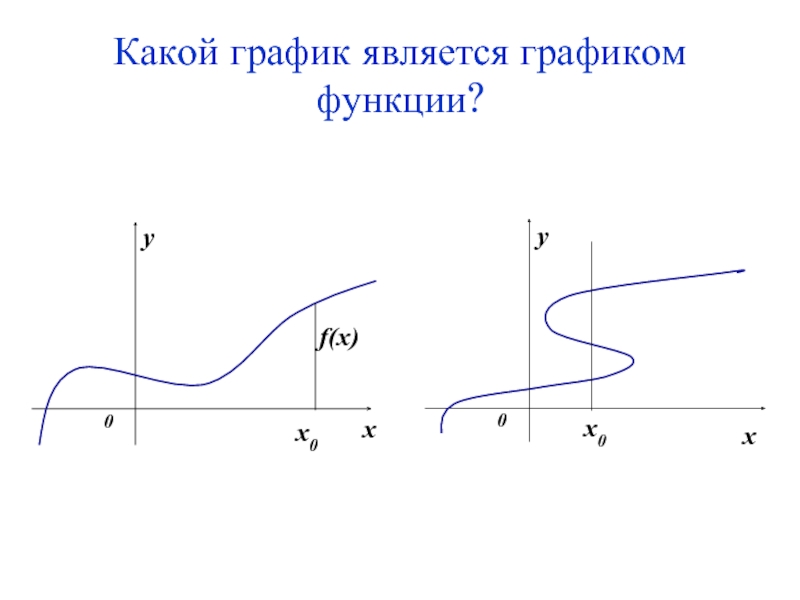
- 5. Какой график является графиком функции? x0
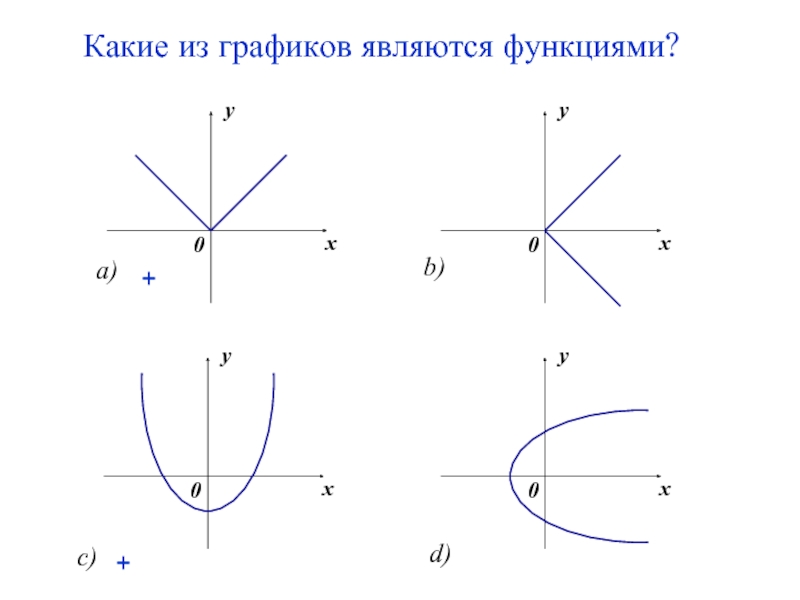
- 6. Какие из графиков являются функциями? c) + +
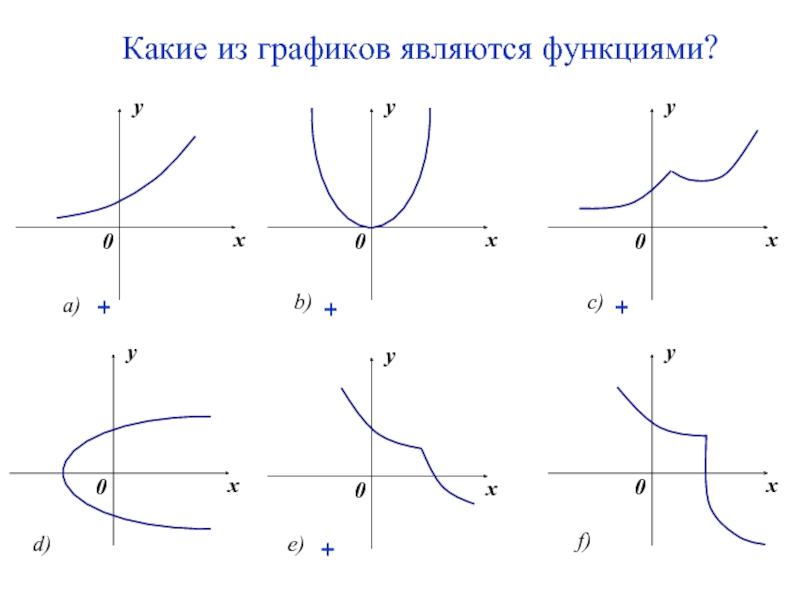
- 7. Какие из графиков являются функциями? + + + +
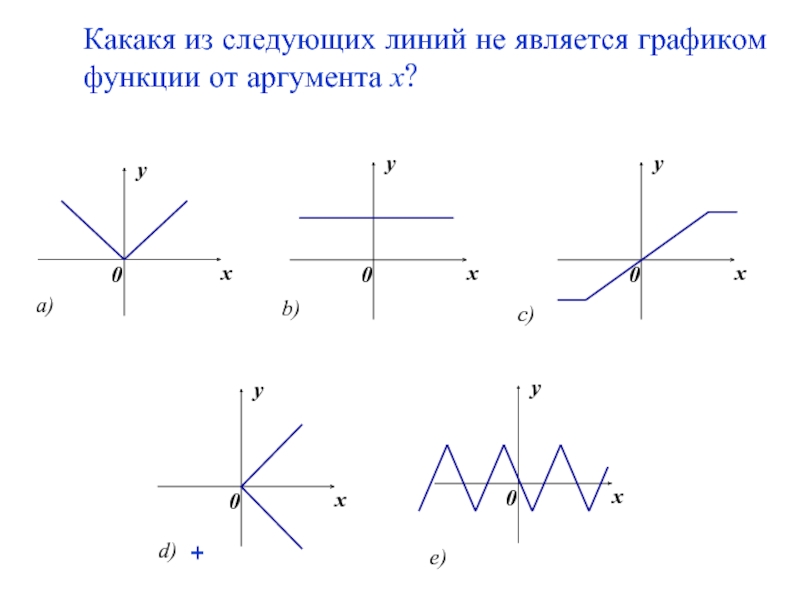
- 8. Какакя из следующих линий не является графиком функции от аргумента х? +
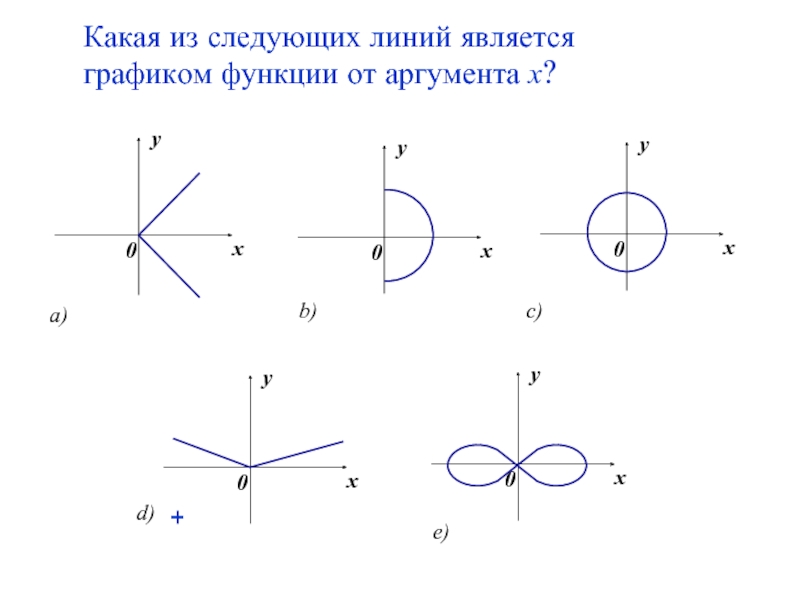
- 9. Какая из следующих линий является графиком функции от аргумента х? +
- 10. Областью определения функции y=f(x) называется множество всех действительных значений аргумента х.
- 11. Укажите область определения функции, изображённой на
- 12. Множество значений функции, изображённой на рисунке
- 13. Особенности отыскания области определения некоторых функций 1).
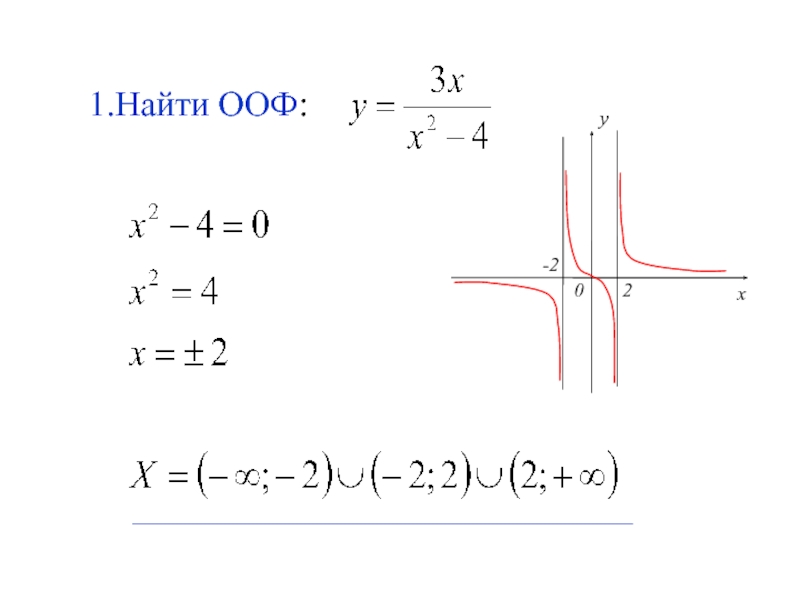
- 14. 1.Найти ООФ: y -2 2 0 x
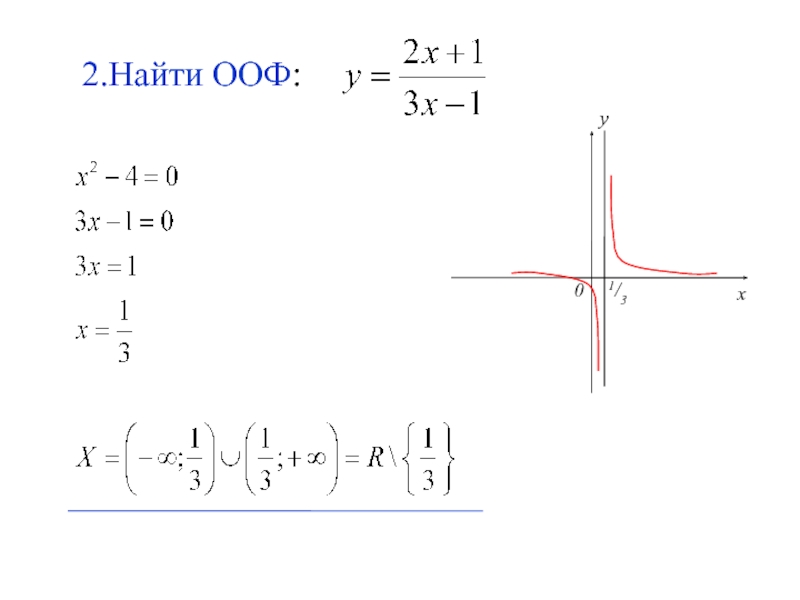
- 15. 2.Найти ООФ: y 1/3 0 x
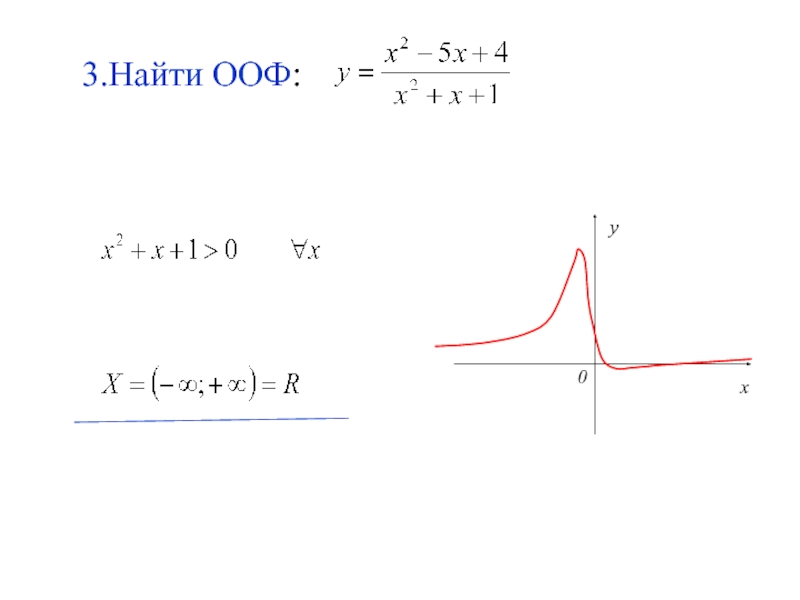
- 16. 3.Найти ООФ: y 0 x
- 17. 2). Если аналитическое выражение функции содержит корень
- 18. Найти область определения функции: пример 5 пример 4 -3
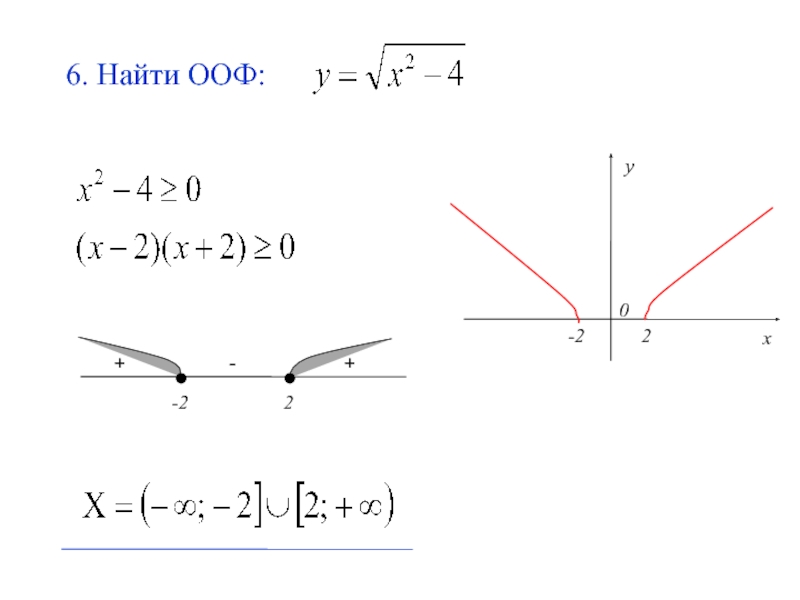
- 19. 6. Найти ООФ:
- 20. 7. Найти ООФ: 0 1 + + -
- 21. 3). Если аналитическое выражение функции содержит логарифм,
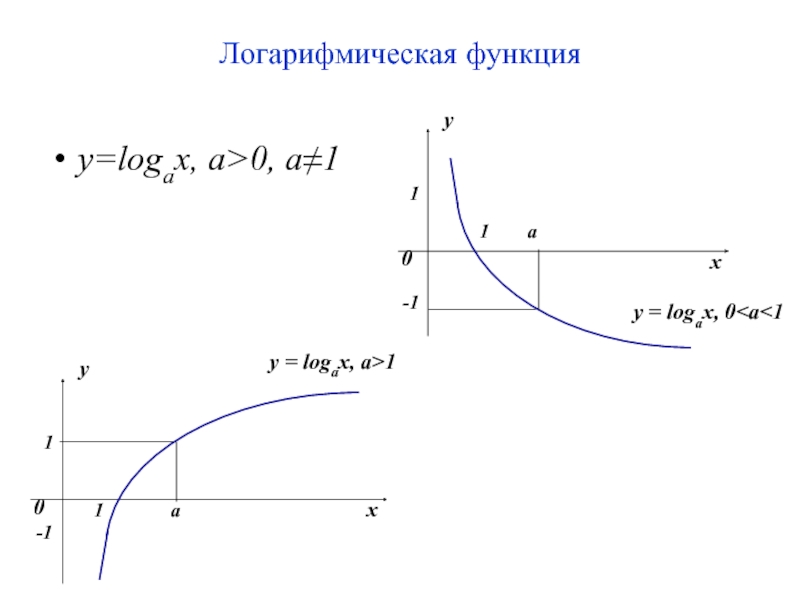
- 22. Логарифмическая функция y=logax, a>0, a≠1
- 23. Найти ООФ: пример 9 пример 8
- 24. 10. Найти ООФ: -3 3 + + -
- 25. 11. Найти ООФ:
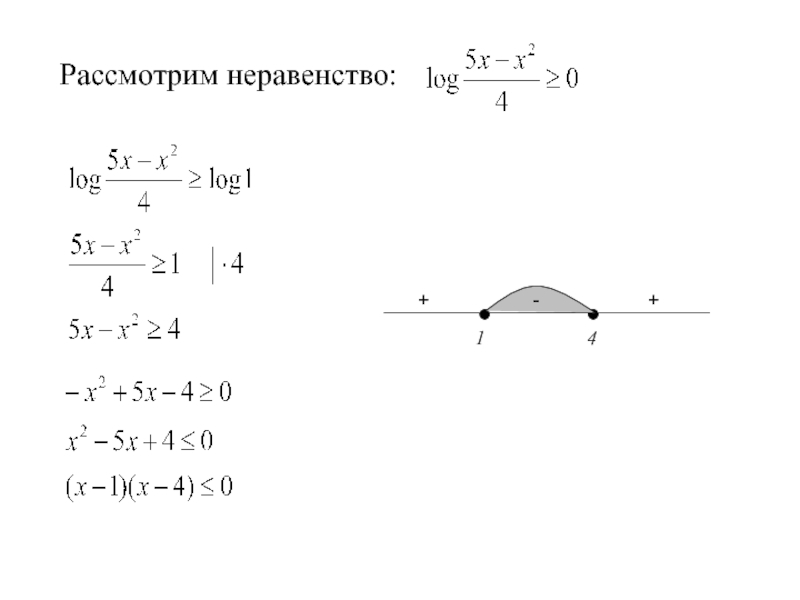
- 26. Рассмотрим неравенство: 1 4 + + - -
- 27. Рассмотрим неравенство: 0 5 -
- 28. 4). Если аналитическое выражение функции содержит обратные
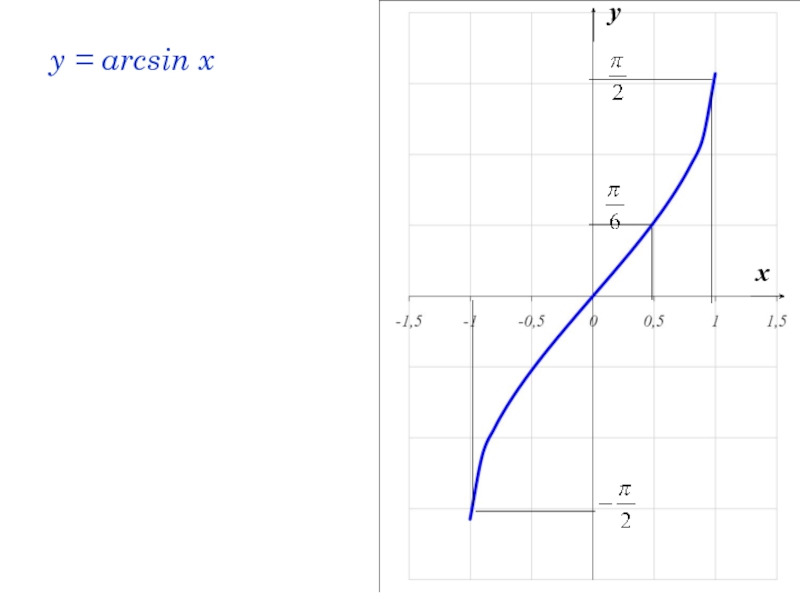
- 29. y = arcsin x
- 30. y = arccos x
- 31. 12. Найти ООФ: -1 5 х у
- 32. 13. Найти ООФ: 3/4 1 + + - -
- 33. 2. Способы задания функции графический способ аналитический
- 34. Иногда рассматривают функции, которые на различных участках
Слайд 21.Определение функции
Пусть заданы множества Х и У.
Если каждому элементу х по
какому-то правилу f, поставлен в соответствие один и только один элемент у, то говорят, что на множестве Х задана функция f со значением из множества У и пишут:
f: X→Y или
f: X→Y или
f
Слайд 3
f
ОБЛАСТЬ
ОПРЕДЕЛЕНИЯ
МНОЖЕСТВО
ЗНАЧЕНИЙ
элементы
x- аргумент или независимая переменная
y- зависимая переменная или функция
f:
X→Y или
Слайд 10
Областью определения функции y=f(x) называется множество всех действительных значений аргумента х.
Слайд 11
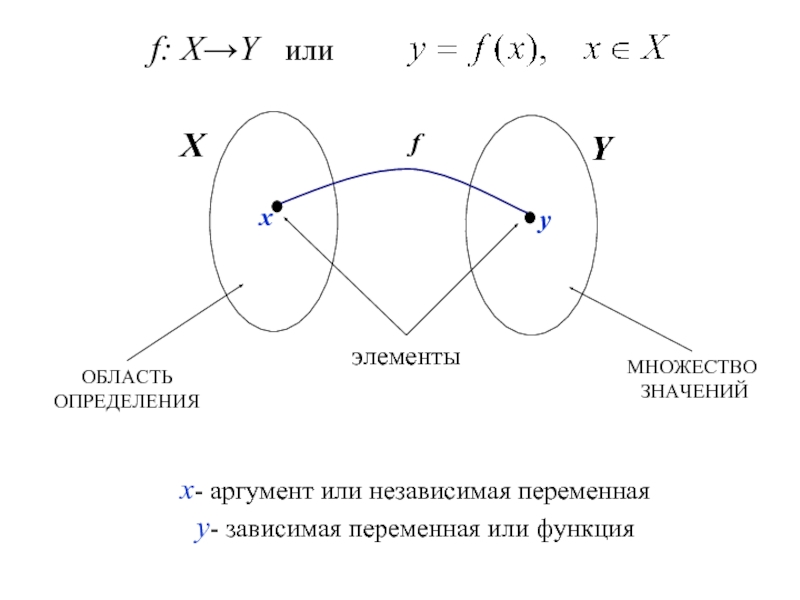
Укажите область определения функции, изображённой на рисунке:
a) [-0,5; 0,5] a) [-1; 1]
b)
(-0,5; 0,5) b) (-1; 1)
c) (-1; 1) c) (-2; 2)
d) [-1; 1] d) [-2; 2]
e) Ответ отличен от приведённых e) Ответ отличен от приведённых
c) (-1; 1) c) (-2; 2)
d) [-1; 1] d) [-2; 2]
e) Ответ отличен от приведённых e) Ответ отличен от приведённых
+
+
1
-1
Слайд 12
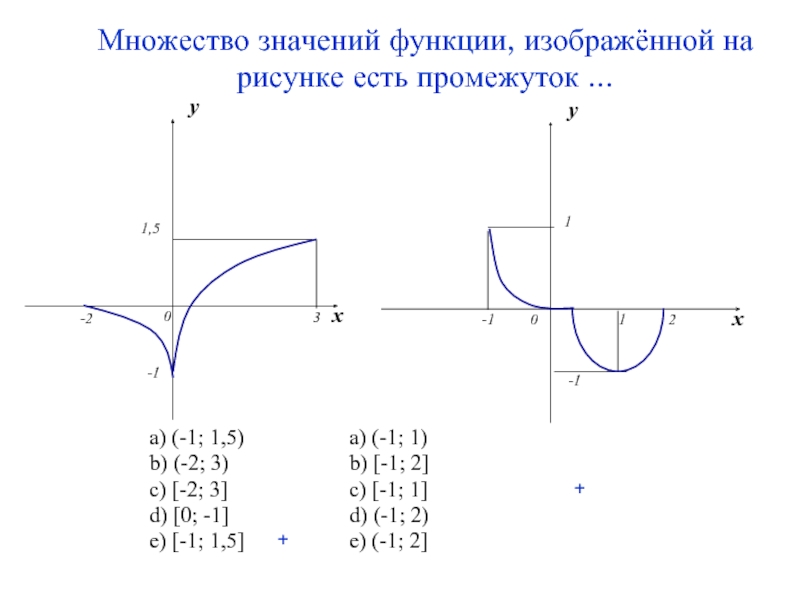
Множество значений функции, изображённой на рисунке есть промежуток ...
a) (-1; 1,5) a)
(-1; 1)
b) (-2; 3) b) [-1; 2]
c) [-2; 3] c) [-1; 1]
d) [0; -1] d) (-1; 2)
e) [-1; 1,5] e) (-1; 2]
b) (-2; 3) b) [-1; 2]
c) [-2; 3] c) [-1; 1]
d) [0; -1] d) (-1; 2)
e) [-1; 1,5] e) (-1; 2]
+
+
Слайд 13Особенности отыскания области определения некоторых функций
1). При отыскании области определения дробной
функции нужно исключить значения аргумента, при которых знаменатель обращается в ноль.
Слайд 172). Если аналитическое выражение функции содержит корень четной степени, то при
отыскании ООФ нужно исключить значения аргумента, при которых подкоренное выражение принимает отрицательное значение (т.е. подкоренное выражение должно быть положительным).
Слайд 213). Если аналитическое выражение функции содержит логарифм, то при отыскании ООФ
нужно исключить значения аргумента, при которых выражение под знаком логарифма принимает отрицательное значение и обращается в ноль (т.е. выражение под знаком логарифма должно быть строго положительным).
Слайд 284). Если аналитическое выражение функции содержит обратные тригонометрические функции arcsin и
arccos, то при отыскании ООФ нужно включать только те значения аргумента, при которых выражения, стоящие под знаком этих функций , по модулю не превосходят единицы.
Слайд 332. Способы задания функции
графический способ
аналитический способ (функция задается при помощи некоторой
формулы)
табличный способ
x
y
0
1
Слайд 34 Иногда рассматривают функции, которые на различных участках изменения х задаются разными
аналитическими формулами:
x
0
у
3
1
2
