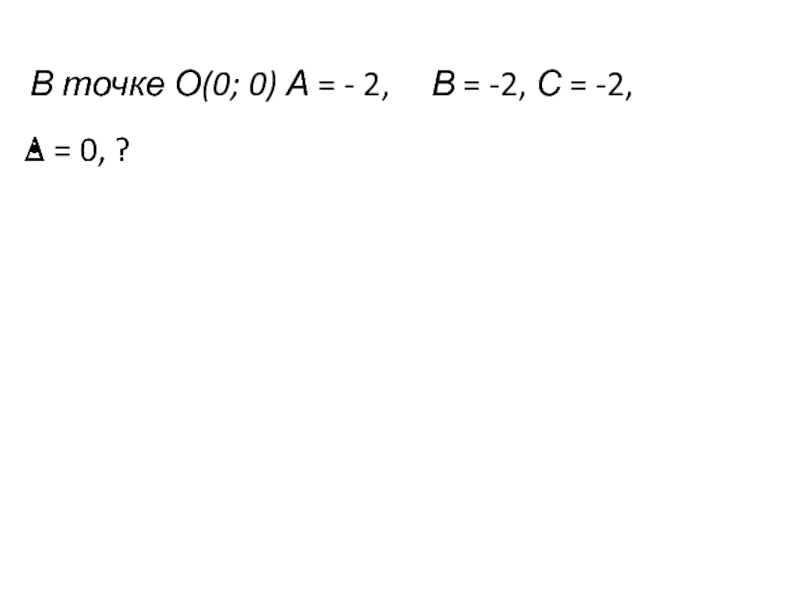Функции нескольких переменных. (Лекция 1) презентация

Содержание

1. Функции нескольких переменных. (Лекция 1)
2. Литература Д. Письменный «Конспект лекций по
3. 1. ФУНКЦИЯ ДВУХ ПЕРЕМЕННЫХ. 1.1. Определение, способы задания А) Табличное задание функции
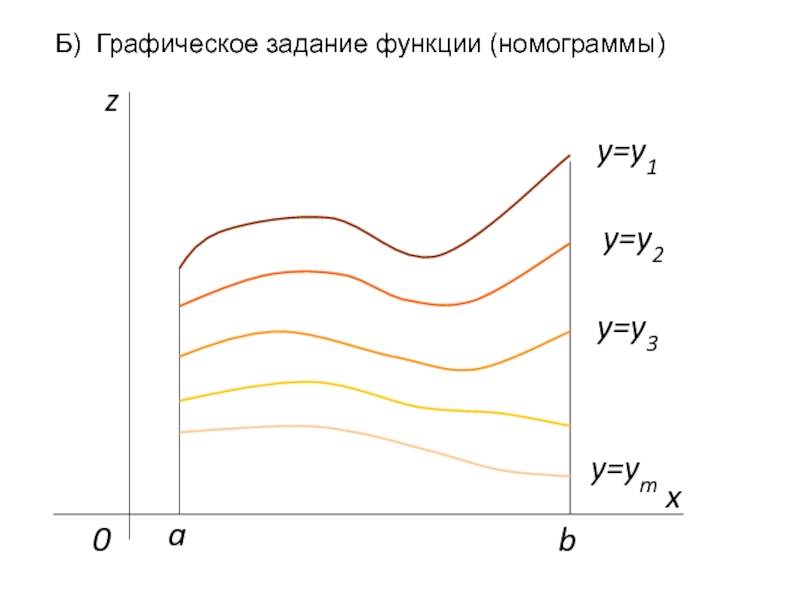
4. Б) Графическое задание функции (номограммы)
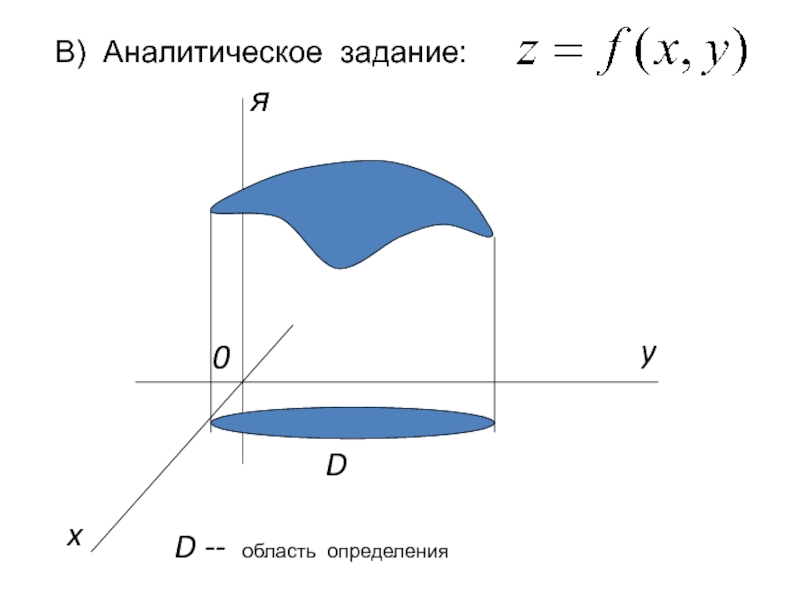
5. В) Аналитическое задание:
6. Определение функции двух переменных
7. Обозначения: При этом пишут: Z = f(x,
8. Опр. Областью определения функции z = f(x, y)
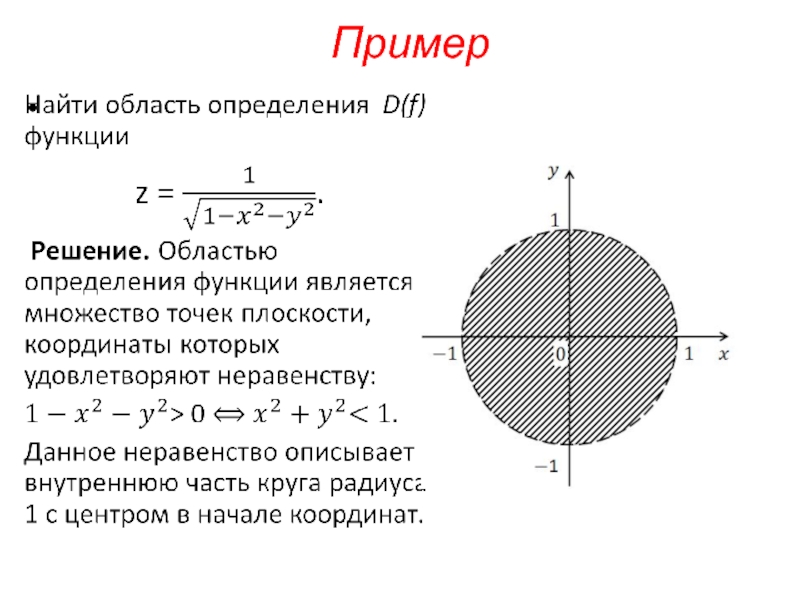
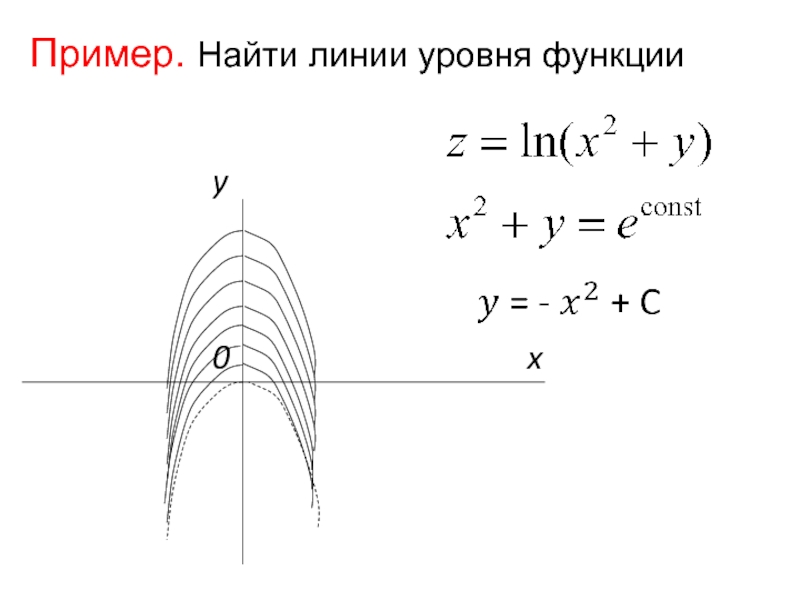
9. Пример
10. График функции Опр. Графиком
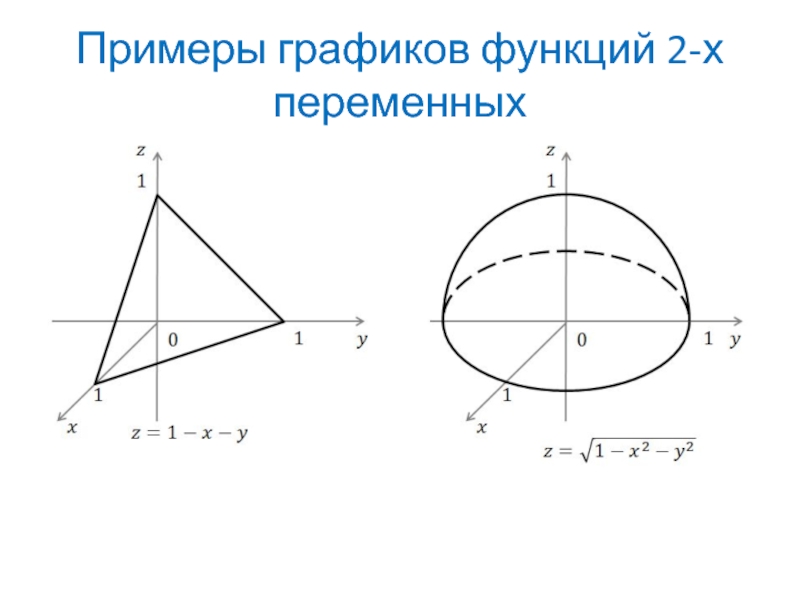
11. Примеры графиков функций 2-х переменных
12. Поверхности и линии уровня
13. x 0 y
14. 2. Предел функции 2-х переменных
15.
16. Пример
17. 3. Непрерывность функции 2-х переменных
18. 4. Частные приращения и производные первого порядка функции двух переменных
19. y=const
20. Определение.
21. x =const
22.
23. Геометрический смысл частных производных функции двух переменных
24. Пример
25.
26. Примеры:
27. 5. Полное приращение и полный дифференциал функции
28. Пример
29. Применение полного дифференциала к приближённым вычислениям
30. Пример
31. 6. Производная сложной функции
32.
33. 2) случай двух независимых переменных .
34. Пример.
35. 7. Производная неявной функции
36. Пример 1.
37. 2) Случай двух независимых переменных
38. Пример
39. 8.Частные производные высших порядков
40.
41. Пример
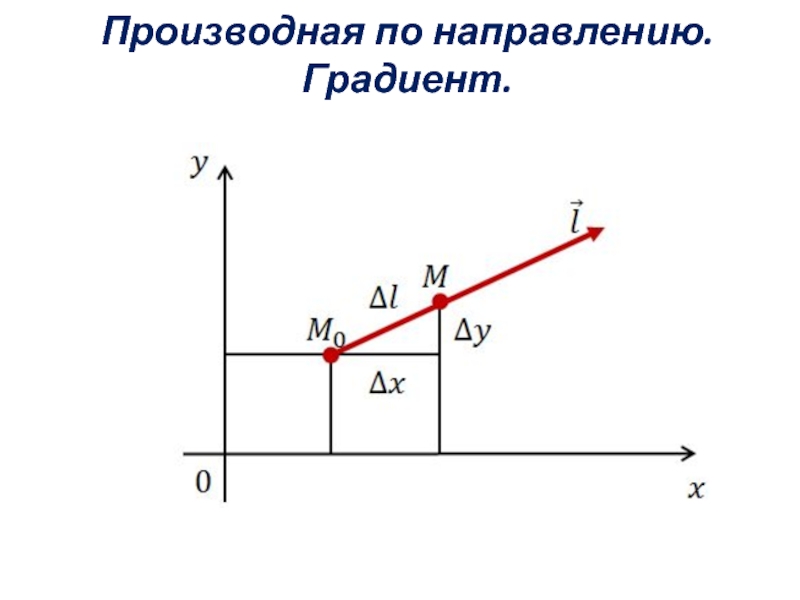
42. 9. Производная по направлению. Градиент.
43. Производная по направлению. Градиент.
44. Производная по направлению. Градиент.
45. Теорема
46. Механический и геометрический смысл производной по направлению
47. Градиент функции
48. Свойства градиента
49. Пример
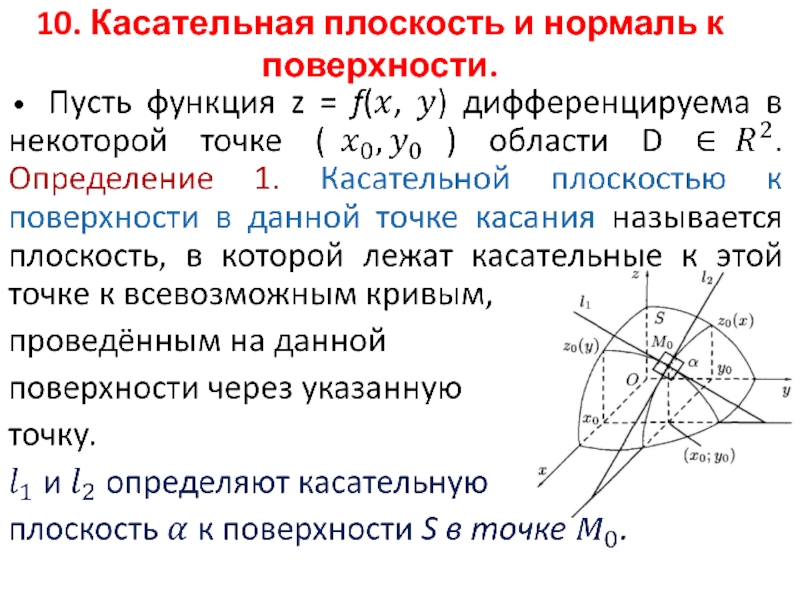
50. 10. Касательная плоскость и нормаль к поверхности.
51. Опр. 2. Нормалью к поверхности называется перпендикуляр к касательной плоскости в точке касания.
52.
53.
54. Замечание.
55. 11. Экстремум функции двух переменных.
56.
57. Достаточные условия существования экстремума функции
58.
59. Пример 1.
60. Пример 2. M1 и M2 -- точки минимума, zmin = -2.
61. В точке О(0; 0) А =

Главная
Математика
Функции нескольких переменных. (Лекция 1)

Слайд 1Лекция №1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Определение функции нескольких переменных.
Предел и непрерывность.
Частные производные

и полный дифференциал.
Производная сложной функции.
Производная неявной функции.
Частные производные и дифференциалы высших порядков.
Производная по направлению и градиент.
Экстремумы функций двух переменных.

Слайд 2Литература
Д. Письменный «Конспект лекций по высшей математике», Ч.1, Ч.2.
2. Н.С. Пискунов

«Дифференциальное и интегральное исчисления», Т. 1, 2.
3. М.В. Ишханян «Математический анализ», Ч.1, 2.
4. Минорский В.П. «Сборник задач по высшей математике».

Слайд 3
1. ФУНКЦИЯ ДВУХ ПЕРЕМЕННЫХ. 1.1. Определение, способы задания
А) Табличное задание функции

Слайд 4Б) Графическое задание функции (номограммы)

z
0
a
b
y=y1
y=y2
y=y3
y=ym
x

Слайд 5
В) Аналитическое задание:

я
x
0
y
D
D -- область определения

Слайд 6 Определение функции двух переменных

Слайд 7Обозначения:
При этом пишут:
Z = f(x, y) или z = z(x, y)

или f: D → ℝ,
где x и y – независимые переменные, z – зависимая переменная (функция).
Определение Множество D(f) называется областью определения функции, а множество значений, принимаемых в области определения функции, называется областью изменения функции Е(f) (или множеством значений).

Слайд 8Опр. Областью определения функции z = f(x, y)

Слайд 9Пример

Слайд 10График функции
Опр. Графиком функции 2-х переменных
z =

f(x, y) является поверхность, проектирующаяся на плоскость XOY в область определения функции (это может быть часть плоскости XOY либо вся плоскость, с границей или без).
z = f(x, y) – аппликата точки М(x, y, z).