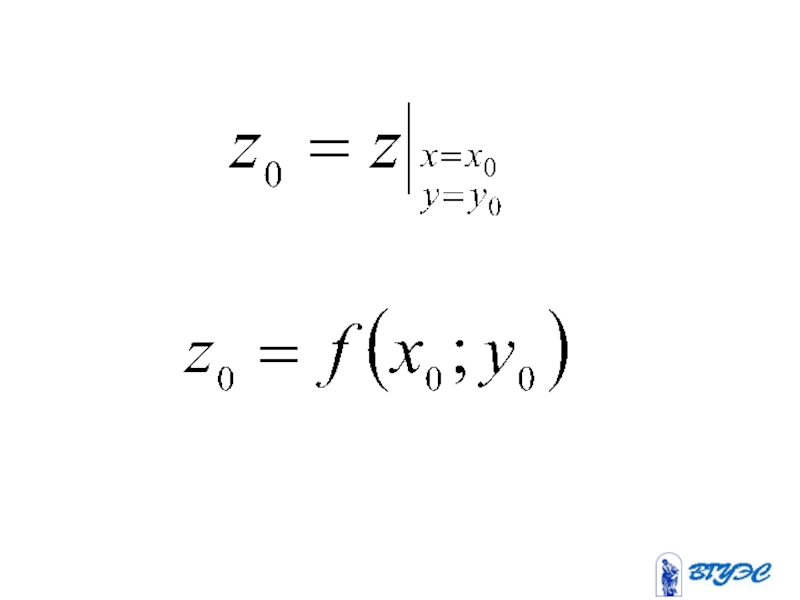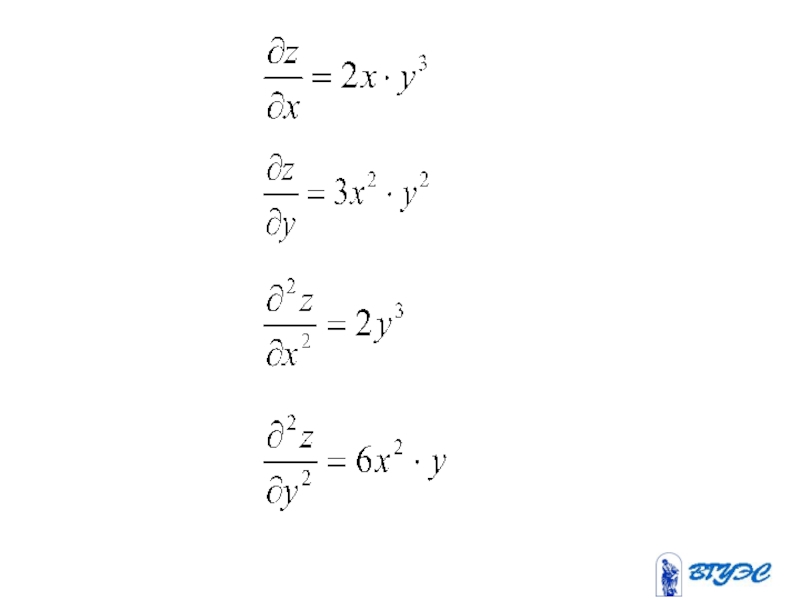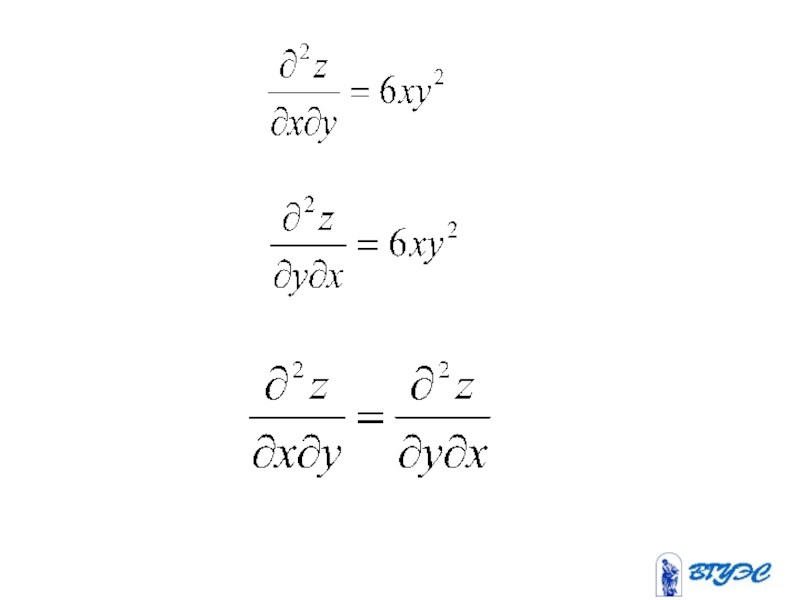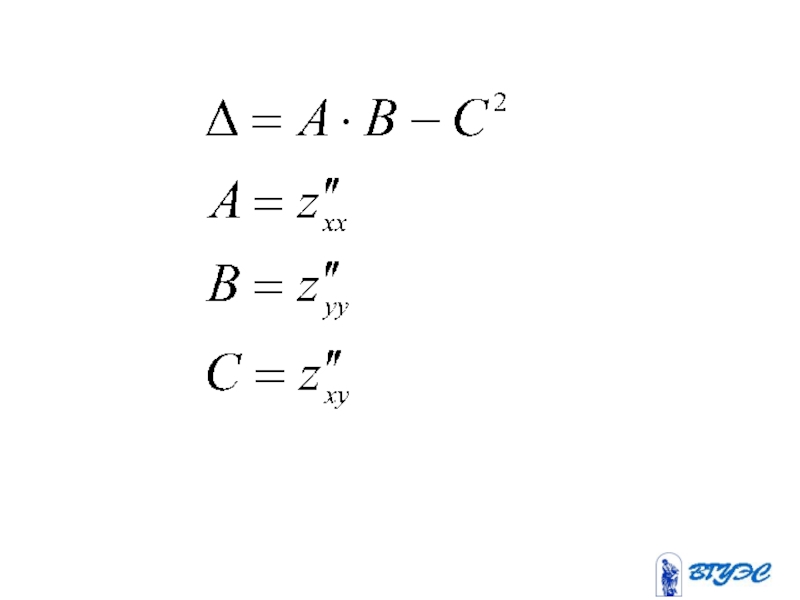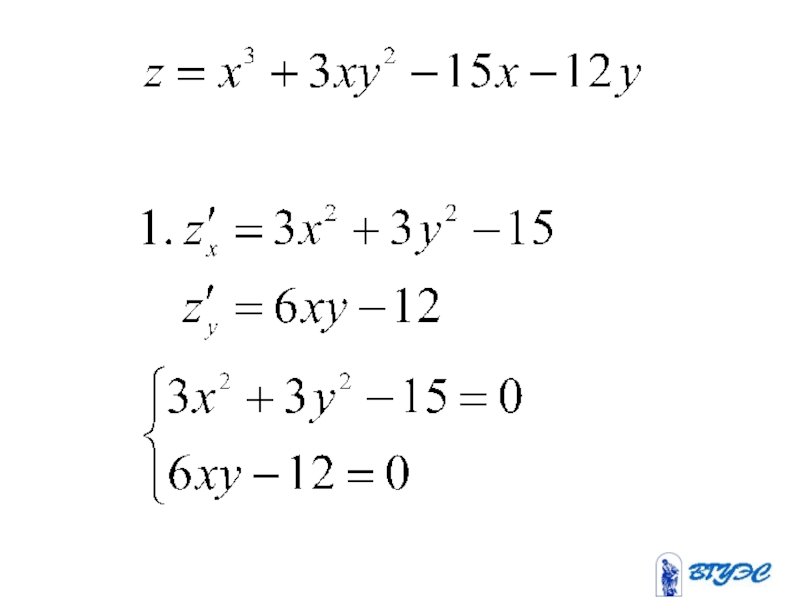- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Функции нескольких переменных презентация
Содержание
- 1. Функции нескольких переменных
- 2. Функцией двух переменных называется правило, по
- 4. Способы задания функции двух переменных Аналитический Табличный Графический
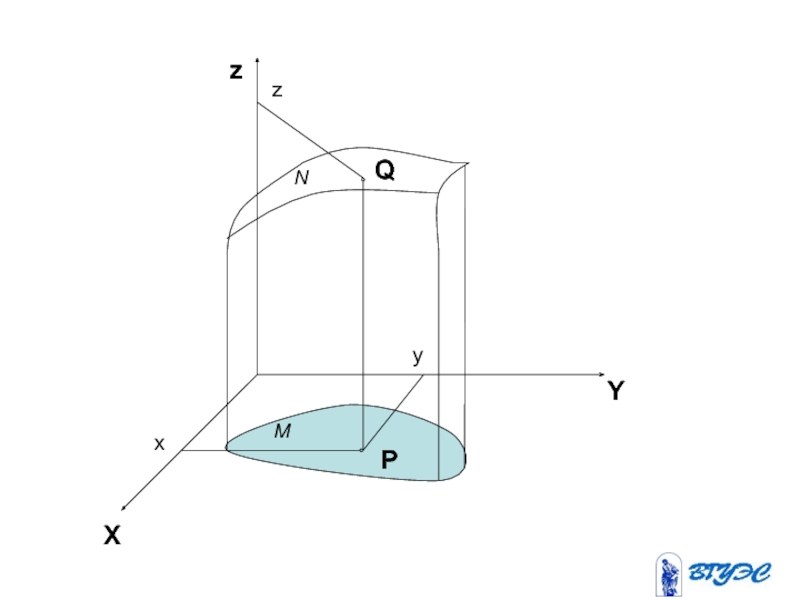
- 5. X Y z x y z P Q M N
- 6. Частные производные
- 7. Рассмотрим функцию
- 8. Предел
- 9. Рассмотрим функцию
- 10. называется частной производной (первого порядка)
- 11. Частные производные высших порядков.
- 12. Пример. Вычислить частные производные второго
- 15. Полный дифференциал.
- 16. Пример. Найти полный дифференциал функции
- 17. Скалярное поле
- 18. Часть пространства (или всё пространство), каждой
- 19. Производная по направлению.
- 20. Градиент
- 21. Экстремум функции двух переменных
- 22. Необходимое условие существования экстремума. Пусть функция
- 23. Достаточное условие существования экстремума
- 24. Пусть для функции
- 26. Возможны три случая:
- 27. =0
- 29. Решая систему ,получим четыре стационарные точки
- 30. Проверим достаточное условие экстремума в каждой из
- 31. 2) Для точки
Слайд 2Функцией двух переменных называется правило,
по которому каждой паре чисел
некоторого
множества М соответствует единственное
число другого множества N.
и - независимые переменные (аргументы);
- зависимая переменная;
М - область определения функции;
N - множество значений функции.
множества М соответствует единственное
число другого множества N.
и - независимые переменные (аргументы);
- зависимая переменная;
М - область определения функции;
N - множество значений функции.
Слайд 7Рассмотрим функцию
Зафиксируем ,тогда функция
примет вид
Пусть аргумент в точке получил
приращение , тогда
Слайд 8Предел
,
если он существует, называется частной
производной (первого порядка) функции
по x в точке и обозначается:
; ; ;
если он существует, называется частной
производной (первого порядка) функции
по x в точке и обозначается:
; ; ;
Слайд 9Рассмотрим функцию
Зафиксируем ,тогда функция
примет вид
Пусть аргумент в точке получил
приращение , тогда
Слайд 18Часть пространства (или всё
пространство), каждой точке
которого соответствует численное значение
некоторой скалярной величины
называется скалярным полем.
Слайд 22Необходимое условие существования экстремума.
Пусть функция
в точке
имеет экстремум и пусть существует
и .
Тогда ,
имеет экстремум и пусть существует
и .
Тогда ,
Слайд 26Возможны три случая:
>0 , тогда точка
– точка
экстремума:
при >0 – точка минимума;
при <0 – точка максимума.
2) <0, тогда не является точкой
экстремума.
экстремума:
при >0 – точка минимума;
при <0 – точка максимума.
2) <0, тогда не является точкой
экстремума.
Слайд 30Проверим достаточное условие экстремума
в каждой из точек.
; ; .
Для точки :
Значит, в точке экстремума нет.
Для точки :
Значит, в точке экстремума нет.