- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Ейлерів й гамільтонів цикл презентация
Содержание
- 1. Ейлерів й гамільтонів цикл
- 2. Зміст Вступ…………………………………………………. 3 Ейлер розв’язав.………………….........………….. ....4 Малій кроки є
- 3. Вступ Початок теорії графів як розділу математики
- 4. Ейлер розв’язав. Його розв’язання, опубліковане 1736 р.,
- 5. Отже, задачу про кенігсберзькі мости мовою
- 6. Ейлерів цикл Ейлеровим циклом у
- 7. Теорема
- 8. Крок
- 9. Алгоритм Флері побудови ейлерового циклу
- 10. Крок
- 11. Гамільтонів цикл у графі
- 12. Кожній
- 13. Інтуїтивно
- 14. Висновки Отже, для задач даного типу покищо
- 15. Список літератури 1. Нікольський Ю. В. Дискретна
Слайд 2Зміст
Вступ…………………………………………………. 3
Ейлер розв’язав.………………….........………….. ....4
Малій кроки є значущими.........……………………..6
Ейлерів цикл…………………………………...……..7
Теорема 1 ………………………………....…….........8
Крок 2. Достатність.................………….......…….9
Гамільтонів цикл…………………........................…10
Цікава
Теорема..........................……………………………...…12
Висновки …………………………………………....14
Список літератури ……………………………….....15
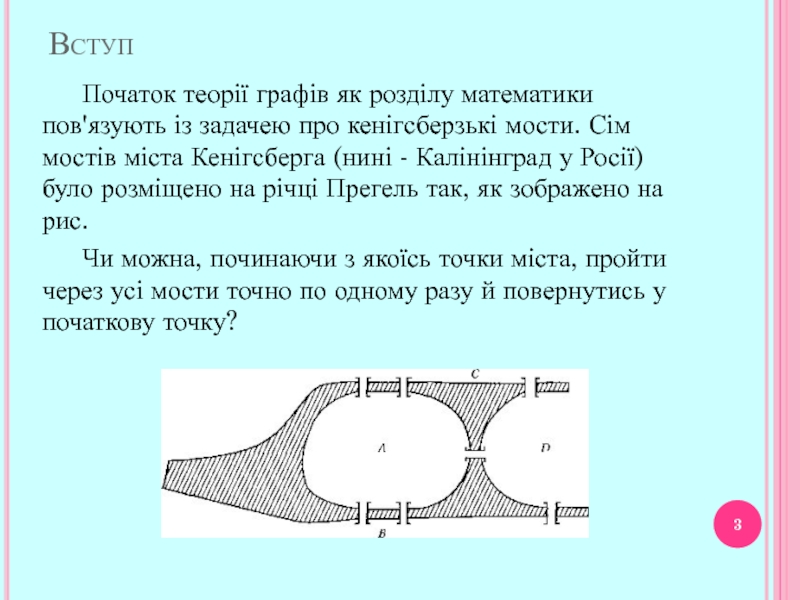
Слайд 3Вступ
Початок теорії графів як розділу математики пов'язують із задачею про кенігсберзькі
Чи можна, починаючи з якоїсь точки міста, пройти через усі мости точно по одному разу й повернутись у початкову точку?
Слайд 4Ейлер розв’язав.
Його розв’язання, опубліковане 1736 р., було першим явним застосуванням теорії
Слайд 5
Отже, задачу про кенігсберзькі мости мовою теорії графів можна сформулювати так:
Ейлер довів нерозв’язність задачі про кенігсберзькі мости. Нагадаємо, що в простому циклі ребра не повторюються, а вершини можуть повторюватись.
Малій кроки є значущими
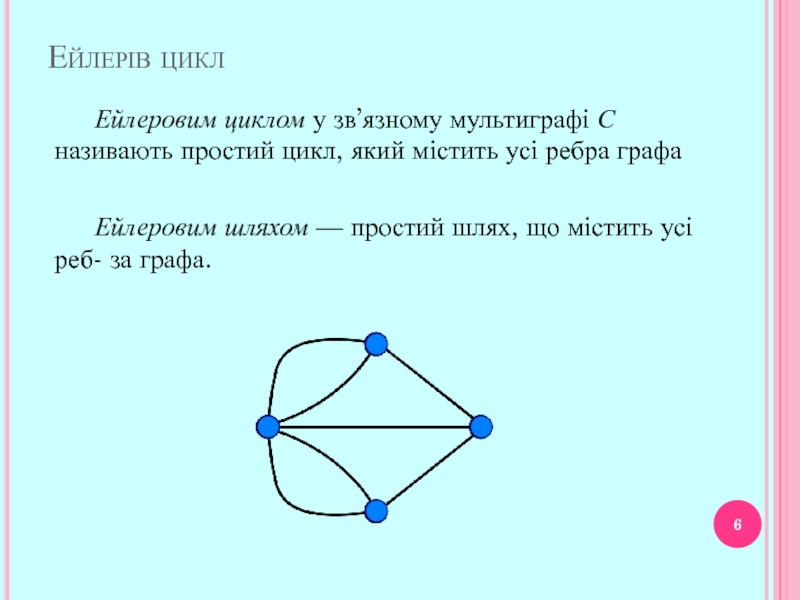
Слайд 6
Ейлерів цикл
Ейлеровим циклом у зв’язному мультиграфі С називають простий цикл, який
Ейлеровим шляхом — простий шлях, що містить усі реб- за графа.
Слайд 7
Теорема 1
Зв’язний мультиграф С має ейлерів цикл тоді
Крок 1. Необхідність. Нехай у графі С існує ейлерів цикл. Він проходить через кожну вершину графа та входить до неї по одному ребру, а виходить по іншому. Це означає, що кожна вершина інцидентна парній кількості ребер ейлерового циклу. Оскільки такий цикл містить усі ребра графа С, то звідси зипливає парність степенів усіх його вершин.
Слайд 8
Крок 2. Достатність
Почнемо шлях P1 із довільної вершини
Отже, побудова шляху Р1 завершиться у вершині v1 тобто Р1 обов’язково ВИЯВИТЬСЯ ЦИКЛОМ.
Слайд 9Алгоритм Флері побудови ейлерового циклу
Робота алгоритму полягає в
Крок 1. Початок. Починаємо з довільної вершини и та присвоюємо довільному ребру {и, v} номер 1. Викреслюємо ребро {и, v} й переходимо у вершину v.
Слайд 10
Крок 2.
Ітерагоя. Нехай v — вершина, у
Крок 3.
Закінчення. Цей процес закінчуємо, коли всі ребра графа викреслено та пронумеровано ці номери задають послідовність ребер в ейлеро вому циклі.
Слайд 11Гамільтонів цикл у графі
Шлях х0, х1 ..., xп_1,хп
G = (V, E) називають гамільтоновим циклом, якщо V = {х0, х1 ..., xп_1,хп} і х1 != х2 для 0 ≤ і ≤ j ≤ п. Цикл х0, х1 ..., xп_1,хп (тут п> 1) у графі G = (V, Е) називають гамільтоновим циклом, якщо х0, х1 ..., xп_1,хп — гамільтонів шлях.
Інакше кажучи, гамільтонів цикл і гамільтонів шлях проходять через кожну вершину графа точно один раз
Слайд 12
Кожній із двадцяти вершин додекаедра (правильного дванадцятигранника, грані
Перехід дозволено
ребрами додекаедра
«Навколосвітня подорож»
Слайд 13
Інтуїтивно зрозуміло, що граф із багатьма ребрами, достатньо
Якщо для кожної вершини v зв’язного простого графа з n ≥ 3 вершинами виконується нерівність deg(v) ≥ п/2, то цей граф має гамільтонів цикл.
Теорема
Слайд 14Висновки
Отже, для задач даного типу покищо не є відомий чіткий алгоритм,
Незважаючи на зовнішню подібність формулювань задач про існування ейлерового й гамільтонового циклів, ці задачі принципово різні. Використовуючи результати попереднього підрозділа, легко виявити, чи має граф ейлерів цикл, і, якщо має, то побудувати його.
Граф, який містить гамільтонів цикл, часто називають гамільтоновим графом.
Слайд 15Список літератури
1. Нікольський Ю. В. Дискретна математика/ Ю. В. Нікольський, В.