- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементы теории множеств презентация
Содержание
- 1. Элементы теории множеств
- 2. План лекции Основные понятия Равные множества Пустое множество Конечное и бесконечное множество Операции над множествами
- 3. Множество – это совокупность некоторых предметов (объектов),
- 4. Перечисление его элементов A = {1; 2;
- 5. Множества, состоящие из конечного числа элементов, называются
- 6. Подмножества Если каждый элемент множества А
- 7. Операции над множествами Объединение множеств Пересечение множеств Разность множеств Дополнение множеств
- 8. Объединение множеств Объединением двух множеств А и
- 9. Пересечение множеств Пересечением (произведением) множеств А и
- 10. Разность множеств Разностью множеств А и В
- 11. Симметрической разностью множеств А и В называется
- 12. Дополнение множеств
- 13. Пусть А и В – конечные множества
Слайд 2План лекции
Основные понятия
Равные множества
Пустое множество
Конечное и бесконечное множество
Операции над множествами
Слайд 3Множество – это совокупность некоторых предметов (объектов), объединенных в одно целое
Предметы, их которых состоит множество называются его элементами
Слайд 4Перечисление его элементов
A = {1; 2; 3; 4; 5; 6; 7;
Указание свойства, по которому можно судить принадлежит элемент множеству или не принадлежит
А = {х|P(х)},
где P(x) — характеристическое свойство
Способы задания множеств
Слайд 5Множества, состоящие из конечного числа элементов, называются конечными множествами. Если же
Множество, не содержащее ни одного элемента, называется пустым множеством (∅).
Множества называются равными, если они состоят из одних и тех же элементов
Слайд 6Подмножества
Если каждый элемент множества А является также элементом множества В,
1. Если А ⊂ B и В ⊂ А, то А = В
2. Пустое множество является подмножеством любого множества: ∅⊂ А
3. Каждое множество есть подмножество самого себя: А ⊂ А
Слайд 7Операции над множествами
Объединение множеств
Пересечение множеств
Разность множеств
Дополнение множеств
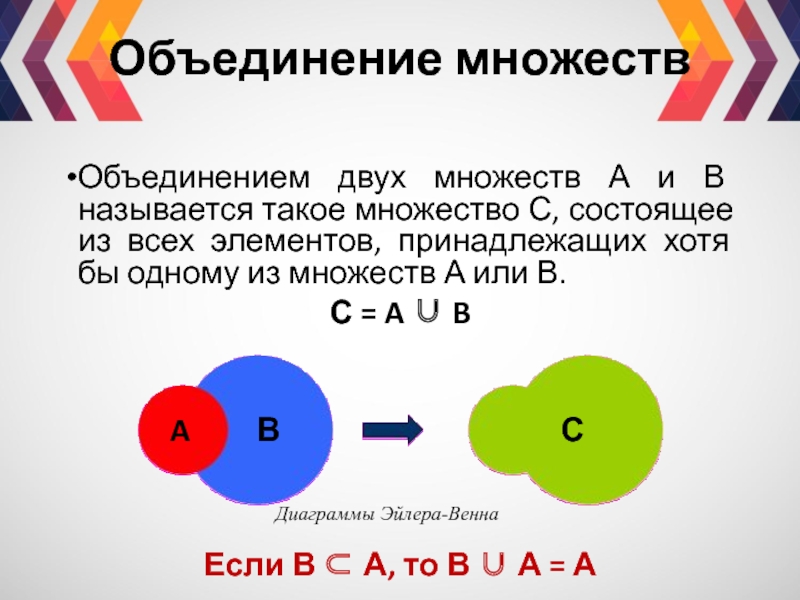
Слайд 8Объединение множеств
Объединением двух множеств А и В называется такое множество С,
С = A ∪ B
Если В ⊂ А, то В ∪ А = А
Диаграммы Эйлера-Венна
Слайд 9Пересечение множеств
Пересечением (произведением) множеств А и В называется множество С, состоящее
A ∩ B = {х | х ∈ A и х ∈ B}
Если В ⊂ А, то В ∩ А = В
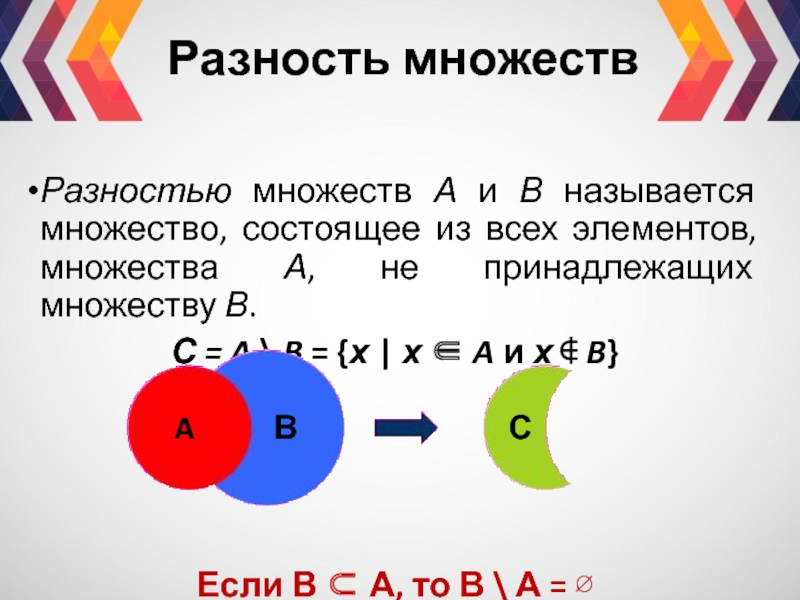
Слайд 10Разность множеств
Разностью множеств А и В называется множество, состоящее из всех
С = A \ B = {х | х ∈ A и х ∉ B}
Если В ⊂ А, то В \ А = ∅
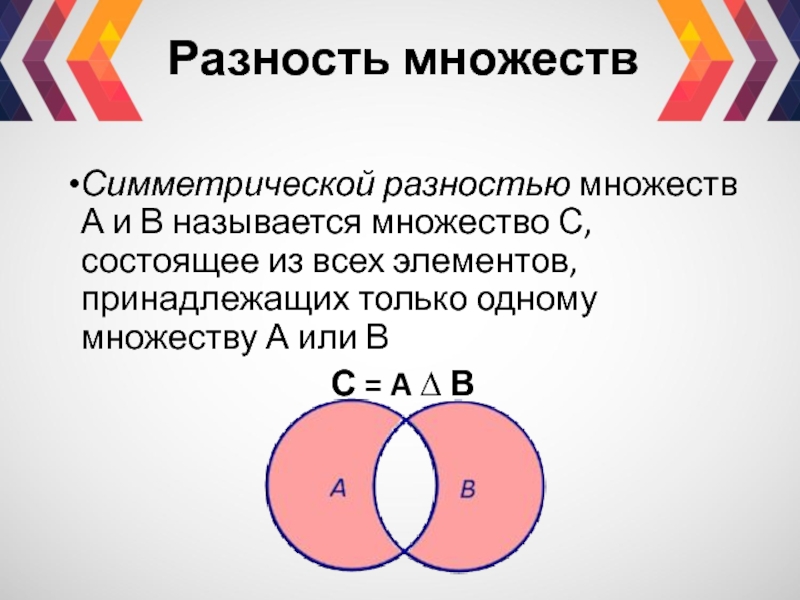
Слайд 11Симметрической разностью множеств А и В называется множество С, состоящее из
С = A ∆ В
Разность множеств
Слайд 13Пусть А и В – конечные множества
mA – число элементов множества
mВ – число элементов множества В, тогда
mA = mA + mB , если A∩В = ∅
mA = mA + mB – mA∩В, если A∪В ≠∅
Формула включений и исключений