3. Первообразная. Неопределенный интеграл и его свойства. Таблица основных интегралов. Методы интегрирования: метод подстановки, метод интегрирования по частям.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементы математического анализа презентация
Содержание
- 1. Элементы математического анализа
- 2. 1.Определение функции, основные понятия 1. Функция
- 3. 3. Область значений функции Множество
- 4. Поведение функции в точке 1.Проколатая окрестность
- 5. Теоремы о пределах 1.Единственность предела Если
- 6. Понятие непрерывности функции. 1.Непрерыв-ность
- 7. Свойства непрерывных функций 1.Функция y=f(x) непрерывна
- 8. March 23, 2020 11-20 13-10
- 9. March 23, 2020 11-25 13-15 Правило
- 10. March 23, 2020 11-40 13-30 1.5.
- 11. March 23, 2020 11-50 13-40 1.6.
- 12. March 23, 2020 Дифференцирование функции
- 13. 12-20 Формулы дифференцирования Формулы дифференцирования
- 14. March 23, 2020 11-25 Формулы дифференцирования
- 15. March 23, 2020 11-35
- 16. 3. Неопределенный интеграл
- 17. Первообразная функция. Неопределенный интеграл и его свойства
- 18. Теорема 1. Если функция
- 19. Геометрический смысл неопределенного интеграла — это совокупность
- 20. Свойства неопределенного интеграла или
- 21. Интегрирование функций. Таблица основных формул интегрирования
- 22. Свойство линейности и методы интегрирования
- 24. Найти интеграл: Решение:
- 25. Определенный интеграл Задача о вычислении площади криволинейной
- 26. площадь всей криволинейной трапеции найдется по
- 27. Если существует конечный предел последовательности интегральных сумм
- 28. Вычисление определенного интеграла В3. Формула Ньютона-Лейбница.
- 29. Вычисление определенного интеграла Интегрирование по частям
- 30. Вычисление определенного интеграла Методы интегрирования. Замена
- 31. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ Пусть функция
- 32. Итак, по определению Если указанный предел
- 33. Несобственные интегралы
Слайд 1Элементы математического анализа
Функция. Область определения функции. Предел функции, непрерывность функции.
2.
Слайд 21.Определение функции, основные понятия
1. Функция
Отображение числового множества D
на числовое множество
y- функция (зависимая переменная)
x- аргумент независимая переменная)
2. Область определения функции
Множество значений x при которых функция y определена.
Слайд 33. Область значений функции
Множество значений функции y для всех
4.
Множество точек плоскоcти
График – это линия в
5. Частное значение функции
Значение функции y при заданном значении аргумента x=a.
Слайд 4Поведение функции в точке
1.Проколатая окрестность точки a
Окрестность точ-ки a, из
4.Предел функции y=f(x) в точке a
Слайд 5Теоремы о пределах
1.Единственность предела
Если предел существует, то он единственен.
2.Связь
3.Предел суммы и разности
4.Предел произведения
5.Предел частного
6.Первый замечательный предел
7.Второй замечательный предел
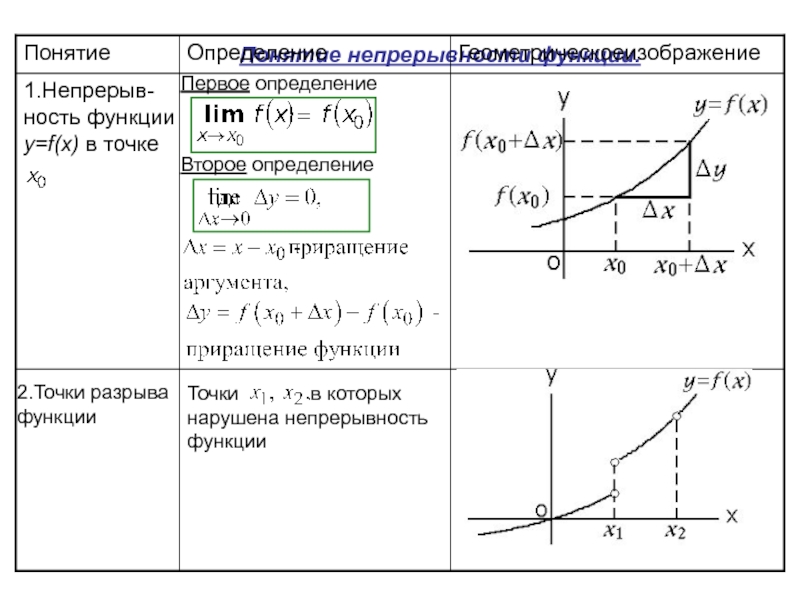
Слайд 6Понятие непрерывности функции.
1.Непрерыв-ность функции y=f(x) в точке
Первое определение
Второе
2.Точки разрыва функции
Точки в которых нарушена непрерывность функции
Слайд 7Свойства непрерывных функций
1.Функция y=f(x) непрерывна в точке
2.Функции y=f(x), y=g(x)
- непрерывны в точке
3. Функция непрерывна на [a,b]
Функция на [a,b]
1) ограничена
2)принимает наибольшее M и наименьшее m значения
3)принимает все промежуточные значения между m и M
Слайд 8March 23, 2020
11-20
13-10
Рассмотрим функцию y = f (x).
Опр.
Производной функции y =
Обозначения:
– ввел Ж.Лагранж
– ввел Г.Лейбниц
Слайд 9March 23, 2020
11-25
13-15
Правило дифференцирования по шагам
1. Дать аргументу x приращение Δx
2. Найти приращение функции
3. Вычислить отношение
4. Найти производную
Слайд 10March 23, 2020
11-40
13-30
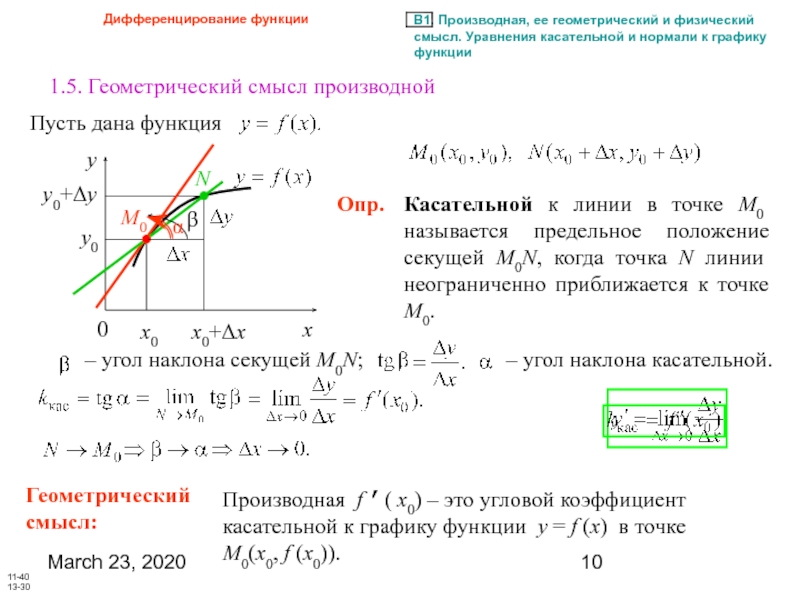
1.5. Геометрический смысл производной
Дифференцирование функции
0
x
y
M0
N
x0
x0+Δx
y0
y0+Δy
β
Опр.
Касательной к
Пусть дана функция
α
– угол наклона секущей M0N;
– угол наклона касательной.
Геометрический
смысл:
Производная f ’( x0) – это угловой коэффициент касательной к графику функции y = f (x) в точке M0(x0, f (x0)).
Слайд 11March 23, 2020
11-50
13-40
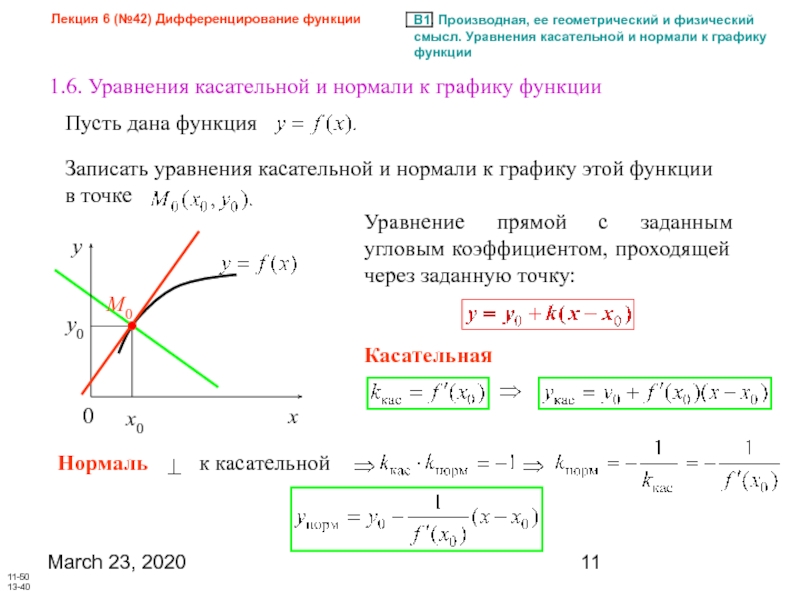
1.6. Уравнения касательной и нормали к графику функции
Лекция 6
Пусть дана функция
0
x
y
M0
x0
y0
Записать уравнения касательной и нормали к графику этой функции в точке
Уравнение прямой с заданным угловым коэффициентом, проходящей через заданную точку:
Касательная
Нормаль
к касательной
Слайд 12March 23, 2020
Дифференцирование функции
Опр.
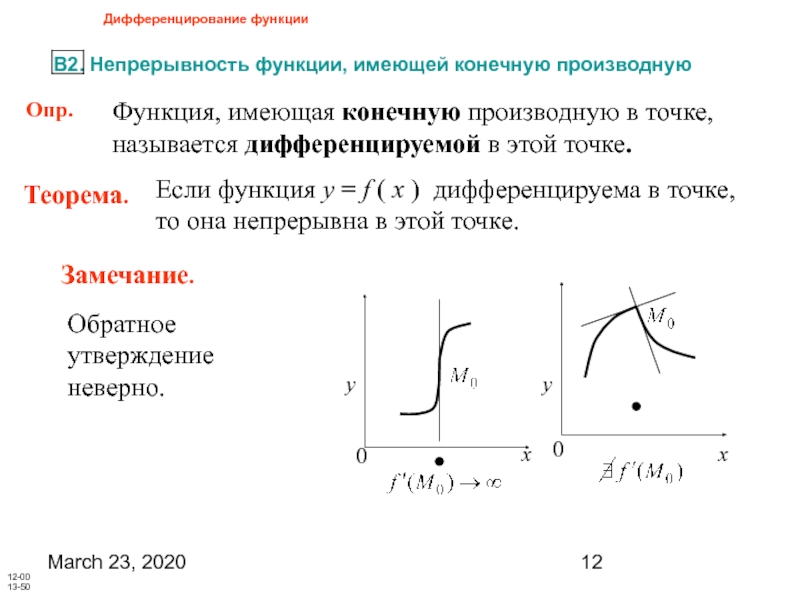
Функция, имеющая конечную производную в точке, называется дифференцируемой
Теорема.
Замечание.
Обратное утверждение неверно.
Если функция y = f ( x ) дифференцируема в точке, то она непрерывна в этой точке.
12-00
13-50
0
x
y
0
x
y
Слайд 14March 23, 2020
11-25
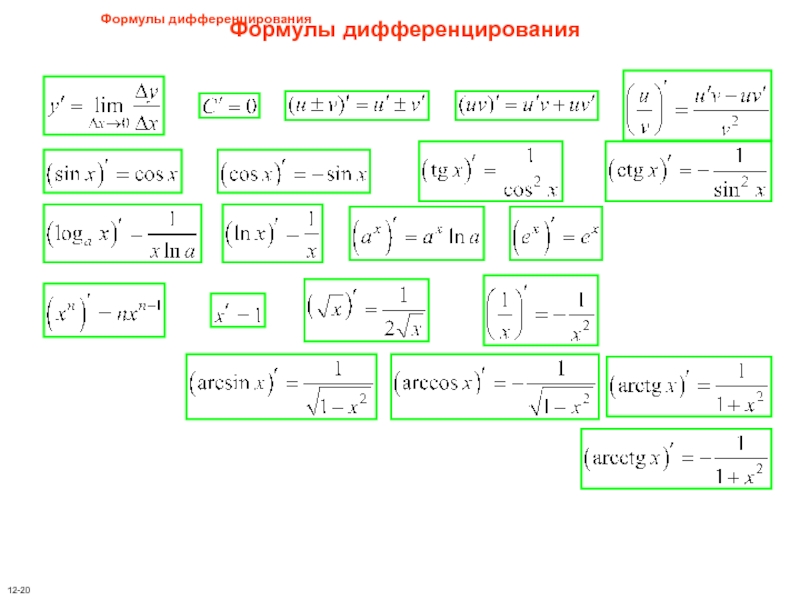
Формулы дифференцирования
Определение.
Переменная u называется промежуточной переменной.
Функции y=f(u)
Примеры.
Сложная функция может состоять из большего числа звеньев:
Два звена.
Пример.
Три звена.
При дифференцировании сложной функции важно уметь представить ее в виде цепочки звеньев.
Пример.
Функция y называется сложной функцией переменной x, если
Слайд 15March 23, 2020
11-35
Теорема.
Если функции y=f (u) и u=g(x) дифференцируемы, то
Правило цепочки.
Примеры.
Замечание.
Слайд 17Первообразная функция. Неопределенный интеграл и его свойства
Функция называется первообразной для
Опр.
Например,
1) для функции
первообразной является функция
2) для функции
3) для функции
Слайд 18Теорема 1. Если функция является первообразной для функции
, где C — произвольная постоянная, также будет первообразной для функции .
Неопределенный интеграл
Определение. Совокупность всех первообразных для функции называется неопределенным интегралом от функции и обозначается
.
Слайд 19Геометрический смысл неопределенного интеграла — это совокупность кривых, получаемых путем сдвига
Например,
— совокупность парабол
Слайд 22Свойство линейности и методы интегрирования
- первообразная
- дифференцируемая функция
Частный случай
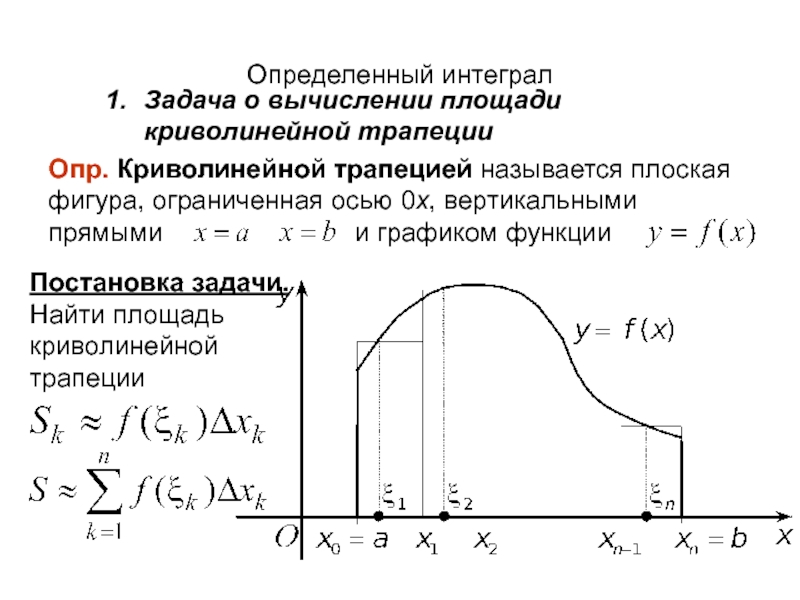
Слайд 25Определенный интеграл
Задача о вычислении площади криволинейной трапеции
Опр. Криволинейной трапецией называется плоская
Постановка задачи. Найти площадь криволинейной трапеции
Слайд 26
площадь всей криволинейной трапеции найдется по приближенной формуле
Перейдя к пределу
Где
называется интегральной суммой для функции на отрезке . Она зависит от способа разбиения отрезка на части и от выбора точек .
Слайд 27Если существует конечный предел последовательности интегральных сумм при
Таким образом, по определению
Число a называется нижним пределом интегрирования, b – верхним пределом интегрирования, отрезок – отрезком интегрирования.
Слайд 28 Вычисление определенного интеграла
В3. Формула Ньютона-Лейбница.
Теорема.
Если F(x) – некоторая первообразная
то справедлива формула
Эта формула называется формулой Ньютона-Лейбница.
.
В3. Формула Ньютона-Лейбница.
Введем знак «двойной подстановки»:
Тогда формулу Ньютона-Лейбница можно записать в виде
Вычисление определенного интеграла
Найти первообразную F(x) для функции f(x) ;
Вычислить разность F(b) – F(a) .
Слайд 29Вычисление определенного интеграла
Интегрирование по частям в определенном интеграле
Теорема.
– непрерывны на
Если
то имеет место формула
которая называется формулой интегрирования по частям
в определенном интеграле.
(3)
,
Методы интегрирования.
Слайд 30Вычисление определенного интеграла
Методы интегрирования.
Замена переменной в определенном интеграле
Теорема.
Пусть дан
где f(x)
, причем
удовлетворяет условиям:
Тогда имеет место формула
(2)
1)
2)
,
– непрерывна на [
.
,
],
Методы интегрирования.
Необходимо запомнить:
1) в определенном интеграле обязательна смена пределов интегрирования
по формулам , ;
2) после нахождения неопределенного интеграла надо вернуться к старой
переменной, а в определенном интеграле этого делать не нужно.
Слайд 31НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Пусть функция непрерывна
рассмотрим определенный интеграл на конечном отрезке .
Опр. Несобственным интегралом от функции
на промежутке называется
и обозначается
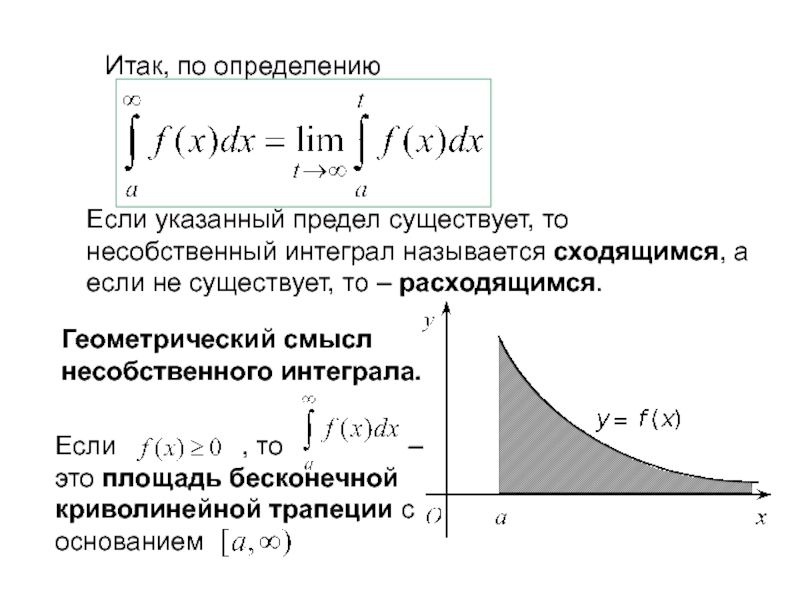
Слайд 32Итак, по определению
Если указанный предел существует, то несобственный интеграл называется сходящимся,
Геометрический смысл несобственного интеграла.
Если , то – это площадь бесконечной криволинейной трапеции с основанием


















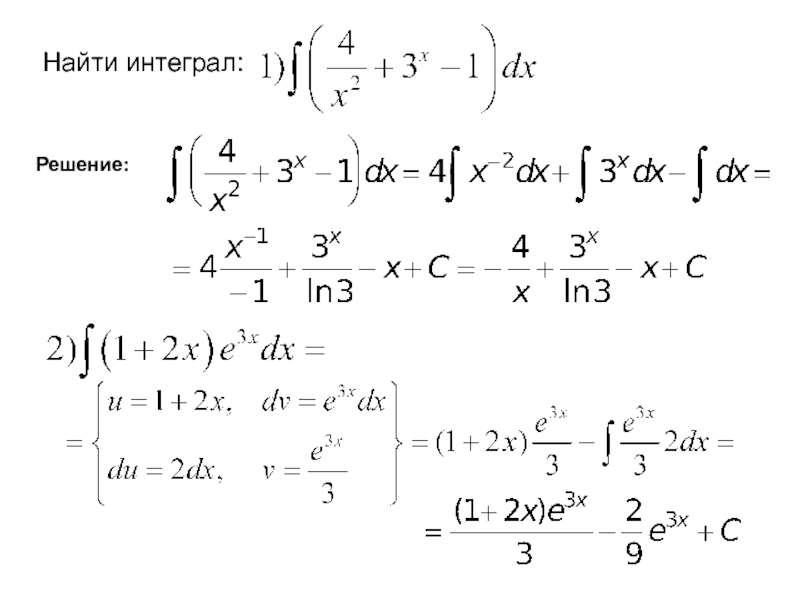



![Вычисление определенного интеграла Интегрирование по частям в определенном интегралеТеорема.– непрерывны на отрезке [ a,b ]](/img/tmb/5/480811/3950e5472ea370f43316932783a0e1f5-800x.jpg)