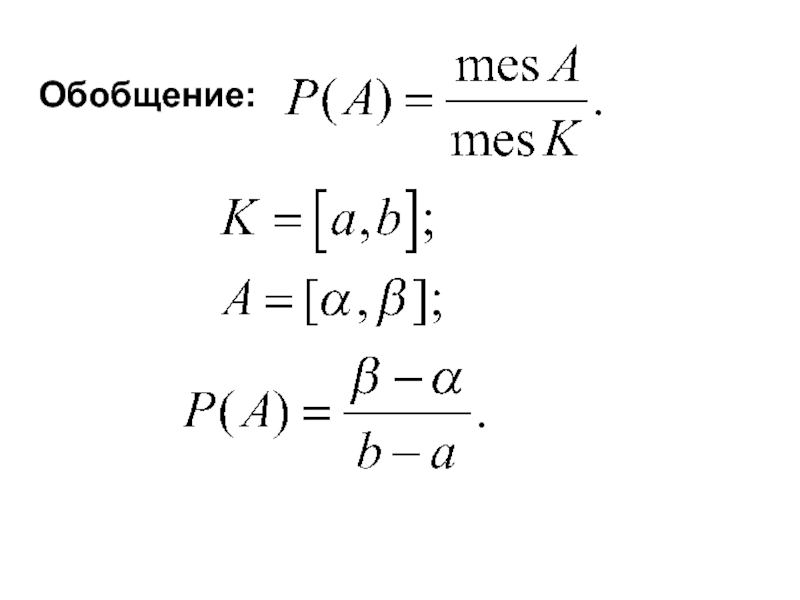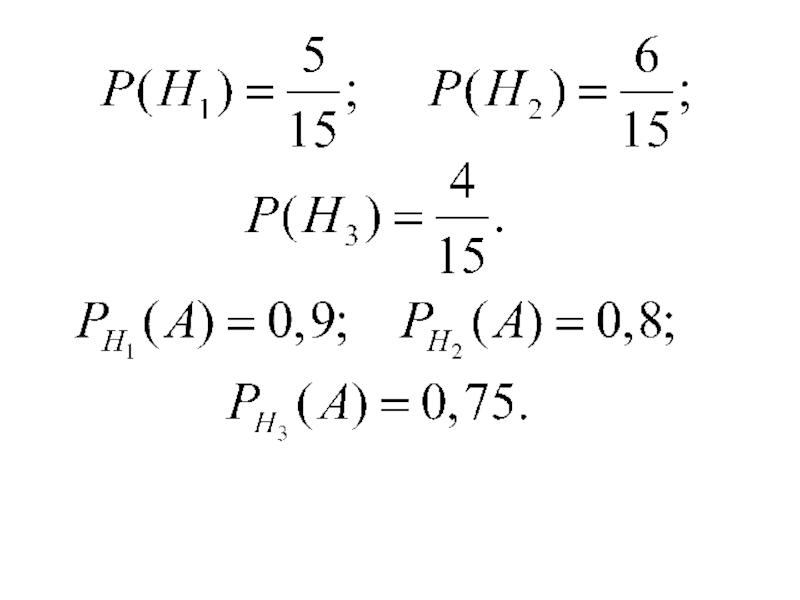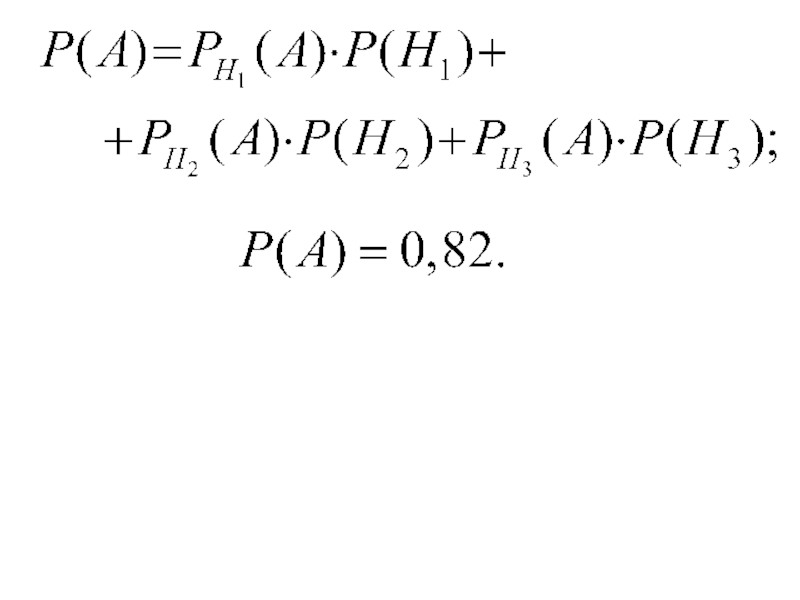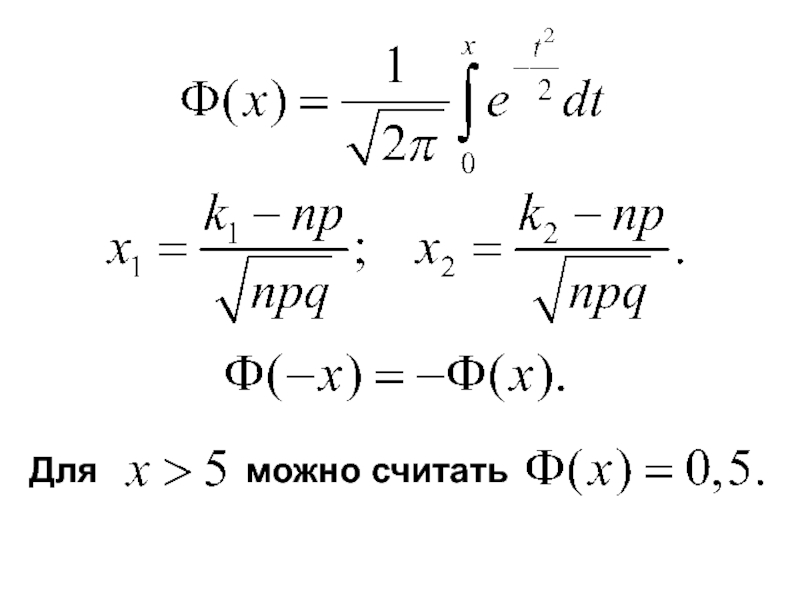изучает число комбинаций из предметов.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементы комбинаторики. (Лекция 1) презентация
Содержание
- 1. Элементы комбинаторики. (Лекция 1)
- 2. Пример. Всего 10 цифр. Сколькими способами можно составить трехзначный номер?
- 3. 3.Сочетания Разные предметы, порядок не важен. Пример.
- 4. 4.Размещения с повторениями. Все важно – и порядок, и предметы, причем их можно повторять.
- 5. 2. Случайные события. Определение 1. Событие называется
- 6. Испытание – это создание условий для возможного
- 8. Пример 2. Кубик с шестью гранями состоит
- 9. Определение 4. Пусть задана полная группа из
- 10. События из полной группы несовместных событий часто
- 11. Если событие состоит
- 12. Классическое определение вероятности. Пусть имеется полная
- 13. Следствие 1. Вероятность невозможного события равна нулю.
- 14. Следствие 2. Вероятность достоверного события равна единице.
- 17. Примеры непосредственного вычисления вероятностей случайных событий. Формула
- 18. Пример 1. Брошена игральная кость. Какова вероятность
- 19. Пример 2. Брошен кубик два раза подряд. Какова вероятность, что оба раза выпадут четные числа?
- 20. Правило умножения. Если комбинация состоит
- 21. Вычислим , то есть перечислим пары
- 22. Лекция №2 Геометрическая вероятность На прошлой лекции
- 23. Например, попадание иглы в точку отрезка. Подобные
- 25. Здесь -- площадь моста,
- 26. Таких полос на квадрате находится 6. Считаем,
- 27. Определение. Пусть даны два множества Считаем,
- 28. Обобщение:
- 29. Замечание. Каждая область состоит из точек. Пусть
- 30. Такие события называются невозможными. Итак,
- 31. Пример. В круге радиуса
- 32. Задача о встрече. Два лица условились
- 33. Решение. Обозначим моменты прихода лица
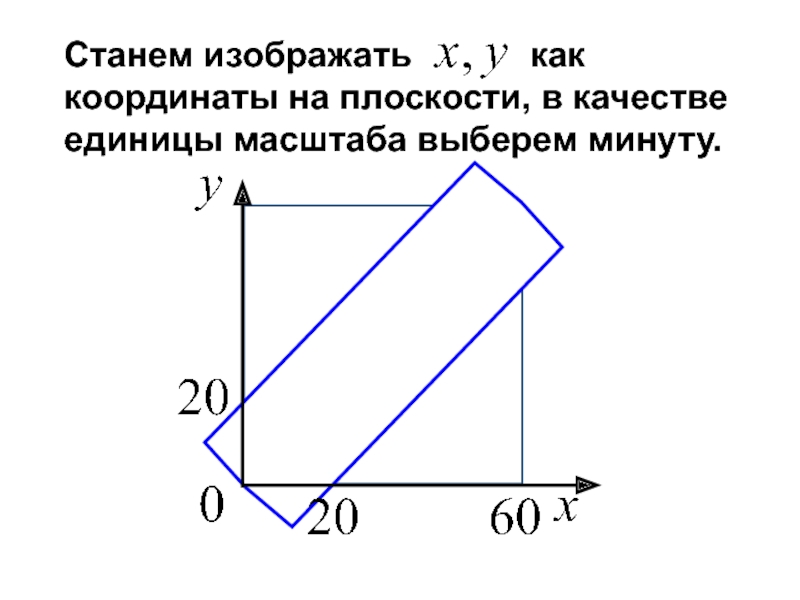
- 34. Станем изображать
- 35. Благоприятные исходы расположены в заштрихованной области.
- 36. Операции над случайными событиями
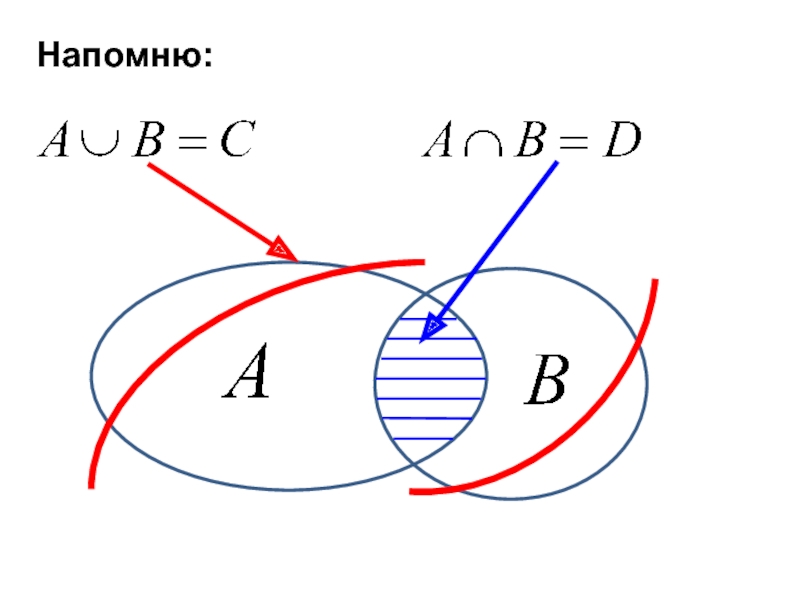
- 37. Напомню:
- 38. Определение 1. Пусть Суммой случайных событий называется
- 39. Лекция №3 Операции над случайными событиями Формула
- 40. Тогда, так как получаем Разделим обе части на площадь
- 41. Определение. Для несовместных событий формула сложения вероятностей принимает вид
- 42. Пример. Стрелок производит выстрел по мишени, состоящей
- 43. 2. Условная вероятность.
- 44. Рассмотрим все благоприятные исходы
- 45. Для условной вероятности или
- 46. Пример. Два стрелка независимо друг от друга
- 47. Это значит, что первый попадает и второй
- 48. С) Хотя бы один попал в цель.
- 49. 3. Формула полной вероятности Пусть даны два
- 51. Так как
- 52. Пример. В группе спортсменов
- 53. Введем событие
- 56. 4. Повторные испытания. Формула Бернулли
- 57. Например, стреляя в одну мишень, можем получить
- 58. Обобщим приведенный пример, произведя испытаний.
- 59. Однако, событие может появляться и
- 60. Теорема. Вероятность того, что в серии из
- 61. Вероятность того, что событие
- 62. Пример. Какова вероятность, что в семье, имеющей
- 63. Лекция №4 Локальная и интегральная теоремы Лапласа
- 64. Теорема 1 (локальная теорема Лапласа). где
- 65. Теорема 2 (интегральная теорема Лапласа). Вероятность
- 66. Для можно считать
- 67. Пример 1. Вероятность поражения мишени при одном
- 68. Тогда
- 69. Пример 2. Вероятность поражения мишени при одном
- 70. Значения функции
- 71. 3.Формула Пуассона. Пусть
- 72. Замечание. Формула Пуассона тем точнее, чем меньше
- 73. По условию
- 74. Самостоятельная работа Задача №1. Найти вероятность того,
- 75. Лекция №5 Дискретная случайная величина
- 76. Закон распределения или ряд распределения дискретной случайной величины задается в виде таблицы
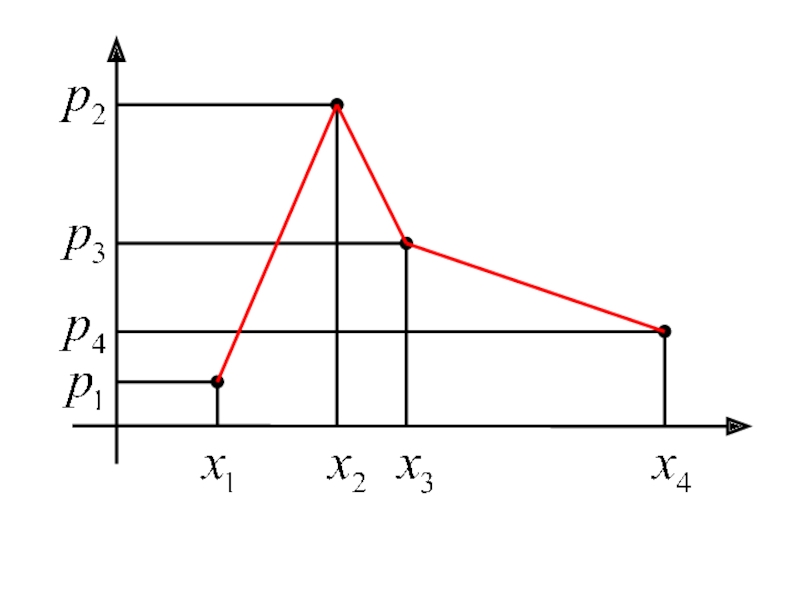
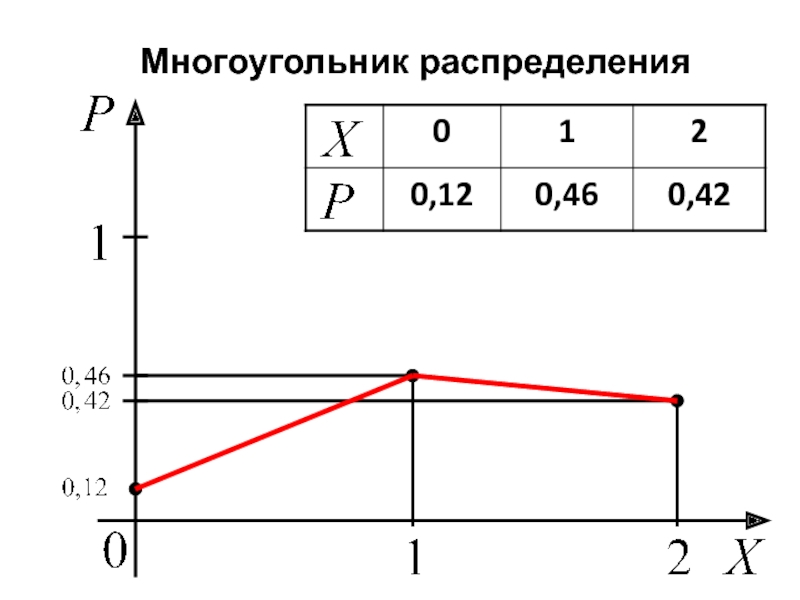
- 77. Многоугольник распределения В системе координат стоят точки
- 79. Пример 1. Два стрелка стреляют по цели
- 80. Пусть -- число попаданий.
- 81. Одно попадание (первый попал и второй
- 82. Многоугольник распределения
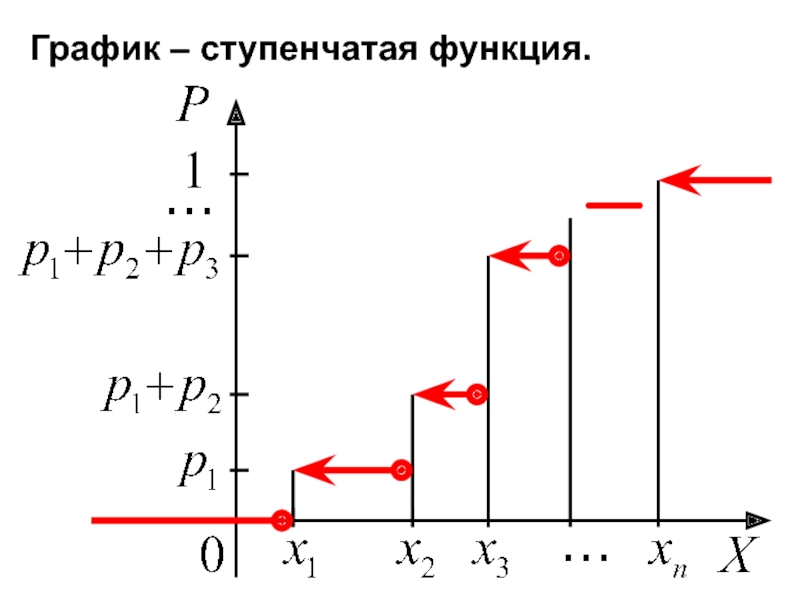
- 83. Функция распределения
- 84. определяется формулой
- 85. График – ступенчатая функция.
- 86. Числовые характеристики дискретной случайной величины Задача. Автомат
- 87. А теперь введем случайную величину – длина гвоздя. Составим ряд распределения.
- 88. Определение. Математическим ожиданием случайной величины называется число
- 89. Свойства 1)
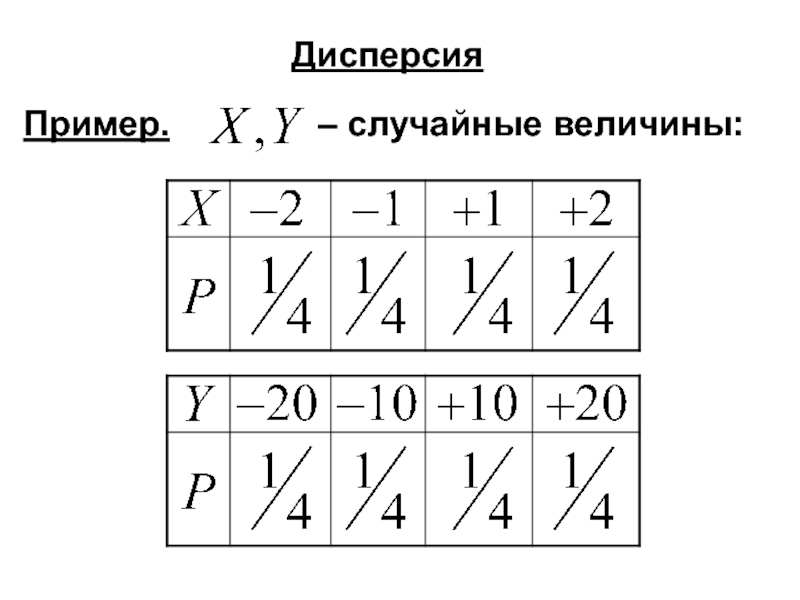
- 90. Дисперсия Пример. – случайные величины:
- 91. Очевидно,
- 92. Для нашего примера:
- 93. Таким образом,
- 94. Свойства 1)
- 95. Примеры законов распределения 1) Биномиальный закон
- 96. 2) Закон Пуассона Если
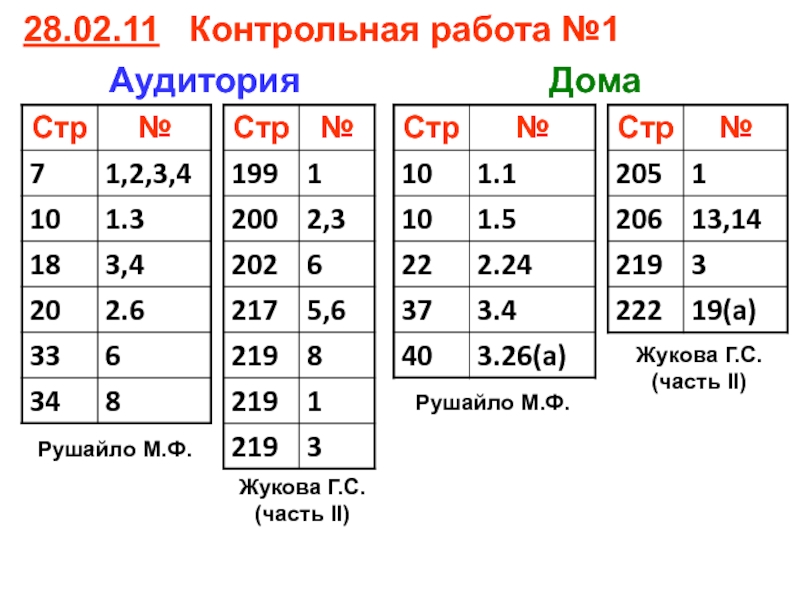
- 97. 28.02.11 Контрольная работа №1 Аудитория Дома
- 98. 1.03.11 Контрольная работа №2 Аудитория Дома
Пример. Всего 10 цифр. Сколькими способами можно составить трехзначный номер?
Слайд 1Теория вероятностей и математическая статистика
Доц.Лаптева Надежда Александровна
Лекция 1
§1. Элементы комбинаторики. Комбинаторика
Слайд 33.Сочетания
Разные предметы, порядок не важен.
Пример. В группе 20 человек. Сколькими способами
можно выбрать
трех делегатов на конференцию?
трех делегатов на конференцию?
Слайд 52. Случайные события.
Определение 1. Событие называется случайным, если оно может произойти,
а может не произойти. Обозначение событий --
Пример 2. Бросаем кубик. Цифры 1,2,3,4,5,6 – случайны.
Пример 1. Бросаем монету. Событие «выпадет герб» является случайным.
Слайд 6Испытание – это создание условий для возможного события. Например, бросить кость,
бросить монету и т.д.
Пример. Бросаем монету. Герб или цифра --- несовместные события.
Определение 2. Два события называются несовместными, если они не могут произойти вместе.
Кубик будем называть игральной костью.
Слайд 7
Пусть задана система из нескольких случайных событий. И пусть все они попарно несовместны. Пусть при испытании обязано появиться одно и только одно из них. Тогда говорят, что задана полная группа событий.
Определение 3.
Слайд 8Пример 2. Кубик с шестью гранями состоит из шести цифр, то
есть на каждой грани написана одна цифра. Эти цифры --- полная группа событий.
Пример 1. Герб и цифра --- полная группа при бросании монеты.
Слайд 9Определение 4. Пусть задана полная группа из событий
И пусть ни одному из них не отдается предпочтения.
Слайд 10События из полной группы несовместных событий часто называют элементарными.
Из элементарных
событий составляют более сложные события --- составные.
Слайд 11Если событие состоит из нескольких элементарных, то
составляющие его элементарные события называют благоприятными.
Их число обозначим
Их число обозначим
Общее число всех элементарных событий в полной группе равновозможных событий обозначим
Слайд 12Классическое определение вероятности.
Пусть имеется полная группа равновозможных несовместных событий. Их число
И пусть случайное событие состоит из
элементарных событий.
элементарных событий.
Слайд 18Пример 1. Брошена игральная кость. Какова вероятность выпадения простого числа?
Перечислим
все простые числа от 1 до 6. Это 1,2,3,5.
Слайд 19Пример 2. Брошен кубик два раза подряд. Какова вероятность, что оба
раза выпадут четные числа?
Слайд 20Правило умножения.
Если комбинация состоит из вариантов, каждый вариант
состоит из
других вариантов то пара
состоит из вариантов.
других вариантов то пара
состоит из вариантов.
Слайд 22Лекция №2
Геометрическая вероятность
На прошлой лекции было введено классическое определение вероятности. Еще
в начале развития теории вероятностей была замечена недостаточность этого определения, так как оно предполагает конечное число исходов. Легко придумать пример с бесконечным числом исходов.
Слайд 23Например, попадание иглы в точку отрезка. Подобные задачи приводят к понятию
геометрической вероятности.
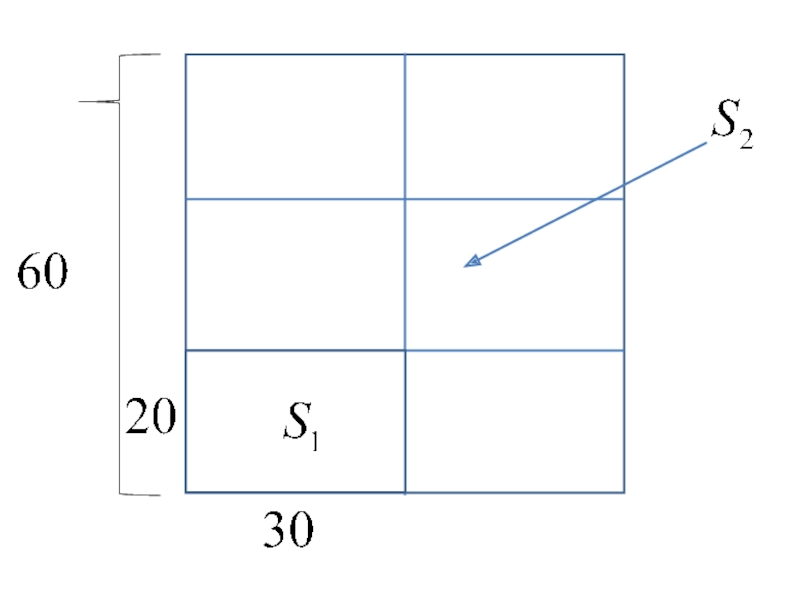
Задача. В так называемый “квадрат рассеяния” со стороной 60 метров падают снаряды. Считаем, что попадание во все точки квадрата равновероятно. В квадрате находится мост размером 30 метров на 20 метров. Какова вероятность попасть в мост?
Слайд 26Таких полос на квадрате находится 6. Считаем, что попадание в каждую
такую
полосу равновероятно и равно
полосу равновероятно и равно
Слайд 27
Определение. Пусть даны два множества
Считаем, что всегда попадаем в множество
Тогда вероятность попасть в множество равна
Слайд 29Замечание. Каждая область состоит из точек. Пусть
-- точка. Какова вероятность попасть в точку
Так как любая мера точки есть нуль, то
Так как любая мера точки есть нуль, то
Такая вероятность называется геометрической вероятностью и приписывается множеству любой размерности.
Слайд 30Такие события называются невозможными.
Итак, бросая иглу, мы попадем в точку,
но вероятность попадания в точку есть нуль, то есть событие невозможное. Приведенное противоречие – один из примеров «парадоксов бесконечности».
Слайд 31Пример. В круге радиуса наудачу появляется точка.
Определить
вероятность того, что она попадает в одну из двух непересекающихся фигур, площади которых равны
Слайд 32Задача о встрече.
Два лица условились встретиться в
определенном месте между 12
и 13 часами. Пришедший первым ждет другого в течение 20 минут, после чего уходит. Чему равна вероятность встречи лиц и
Если приход каждого из них может произойти наудачу и моменты прихода независимы.
Если приход каждого из них может произойти наудачу и моменты прихода независимы.
Слайд 36Операции над
случайными событиями
Геометрическое определение вероятности дает возможность привлечь множества
и операции над ними, именно, объединение и пересечение.
Слайд 38Определение 1. Пусть
Суммой случайных событий называется третье событие
состоящее в наступлении хотя бы одного из первых двух событий.
Слайд 42Пример. Стрелок производит выстрел по мишени, состоящей из двух колец: 10
и 9. Вероятность попадания в 10 равна
Вероятность попадания в 9 равна
Какова вероятность попасть в мишень?
Вероятность попадания в 9 равна
Какова вероятность попасть в мишень?
Слайд 432. Условная вероятность.
означает вероятность события при условии, что событие произошло.
Пример. Брошены две игральные кости. Чему равна вероятность, что сумма выпавших очков равна 8 (событие ), если известно, что выпадает четное число (событие )?
Пример. Брошены две игральные кости. Чему равна вероятность, что сумма выпавших очков равна 8 (событие ), если известно, что выпадает четное число (событие )?
Слайд 46Пример. Два стрелка независимо друг от друга стреляют по цели. Вероятность
попадания для первого
для второго
Найти вероятности следующих событий.
для второго
Найти вероятности следующих событий.
А) оба стрелка попадут в цель.
Слайд 47Это значит, что первый попадает и второй не попадает или наоборот,
то есть второй попадает и первый не попадает. В этом случае
В) только один попадет в цель.
Слайд 52Пример. В группе спортсменов 5 лыжников, 6
велосипедистов и
4 бегуна.
Вероятность выполнить квалификационную норму: для лыжника – 0,9; для велосипедиста – 0,8; для бегуна – 0,75.
Вероятность выполнить квалификационную норму: для лыжника – 0,9; для велосипедиста – 0,8; для бегуна – 0,75.
Найти вероятность, что спортсмен, выбранный наудачу, выполнит норму.
Слайд 53Введем событие
--- спортсмен выполнит
норму.
Гипотезы:
--- лыжник,
--- велосипедист,
--- бегун.
Гипотезы:
--- лыжник,
--- велосипедист,
--- бегун.
Слайд 57Например, стреляя в одну мишень, можем получить
(попал, не попал, попал).
Получилось новое событие, которое называется повторным испытанием.
Получилось новое событие, которое называется повторным испытанием.
Слайд 60Теорема. Вероятность того, что в серии из испытаний событие
появится раз, вычисляется по формуле Бернулли
Слайд 61Вероятность того, что событие
произойдет
не менее раз в серии из опытов, вычисляется по формуле
Слайд 62Пример. Какова вероятность, что в семье, имеющей 5 детей, будут 2
мальчика? Вероятности рождения детей считать одинаковыми.
Слайд 65Теорема 2 (интегральная теорема Лапласа).
Вероятность
того, что событие наступит от до раз в серии из одинаковых независимых испытаний приближенно вычисляется по формуле Лапласа
Слайд 67Пример 1. Вероятность поражения мишени при одном выстреле равна 0,8. Найти
вероятность того, что при 100 выстрелах мишень будет поражена ровно 75 раз.
Слайд 69Пример 2. Вероятность поражения мишени при одном выстреле равна 0,8.
Найдите
вероятность того, что при 100 выстрелах мишень будет поражена не менее 75 и не более 90 раз.
Слайд 72Замечание. Формула Пуассона тем точнее, чем меньше
и больше причем
Пример. Учебник издан тиражом 100000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0001. Найти вероятность того, что тираж содержит ровно 5 бракованных книг.
Слайд 74Самостоятельная работа
Задача №1.
Найти вероятность того, что событие наступит
1400 раз в 2400 испытаниях, если появления этого события в каждом испытании равна 0,6.
Задача №2. Вероятность появления события в каждом из 100 независимых испытаний равна 0,8. Какова вероятность, что событие появится не более 74 раз?
Задача №2. Вероятность появления события в каждом из 100 независимых испытаний равна 0,8. Какова вероятность, что событие появится не более 74 раз?
Слайд 76Закон распределения или ряд распределения дискретной случайной величины задается в виде
таблицы
Слайд 77Многоугольник распределения
В системе координат стоят точки
где Соединяют эти точки последовательно прямыми. Получают ломаную, которую и называют многоугольником распределения.
Слайд 79Пример 1. Два стрелка стреляют по цели по одному разу. Вероятность
попадания:
для первого стрелка 0,6;
для второго – 0,7.
Найдите закон распределения и постройте многоугольник распределения.
Найдите закон распределения и постройте многоугольник распределения.
Слайд 80Пусть -- число попаданий. -- случайная
величина, принимает значения 0, 1, 2.
Найдем соответствующие вероятности.
Найдем соответствующие вероятности.
Ноль попаданий:
(первый не попал и второй не попал)
Слайд 81Одно попадание (первый попал и второй не попал, или первый
не попал и второй попал):
Два попадания (первый попал и второй попал):
Слайд 86Числовые характеристики дискретной случайной величины
Задача. Автомат режет гвозди из проволоки. Всего
100 гвоздей. 50 гвоздей длиной 10 см; 40 гвоздей – 9 см; 10 гвоздей – 11 см. Найти среднюю длину гвоздя.
Слайд 962) Закон Пуассона
Если велико, а вероятность
появления события в каждом испытании очень мала, то
где
где
Слайд 9728.02.11 Контрольная работа №1
Аудитория
Дома
Рушайло М.Ф.
Жукова Г.С.
(часть II)
Рушайло М.Ф.
Жукова Г.С.
(часть II)
Слайд 981.03.11 Контрольная работа №2
Аудитория
Дома
Рушайло М.Ф.
Жукова Г.С.
(часть II)
Рушайло М.Ф.
Жукова Г.С.
(часть II)
