- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Двухфакторный дисперсионный анализ презентация
Содержание
- 1. Двухфакторный дисперсионный анализ
- 2. Пример Компания хочет проверить эффективность своей рекламы.
- 3. Пример При α = 0,01 проанализируйте данные, используя двусторонний дисперсионный анализ.
- 4. Дисперсионный анализ (Analysis of Variance) F-критерий, который
- 5. Однофакторный и двухфакторный анализ Дисперсионный анализ, который
- 6. 11-1. Двухфакторный дисперсионный анализ Описание метода и пример
- 7. Постановка проблемы При применении двухфакторного дисперсионного анализа
- 8. Эффект обработки и эффект взаимодействия Исследуемые группы
- 9. Эффект обработки и эффект взаимодействия Двухфакторный дисперсионный
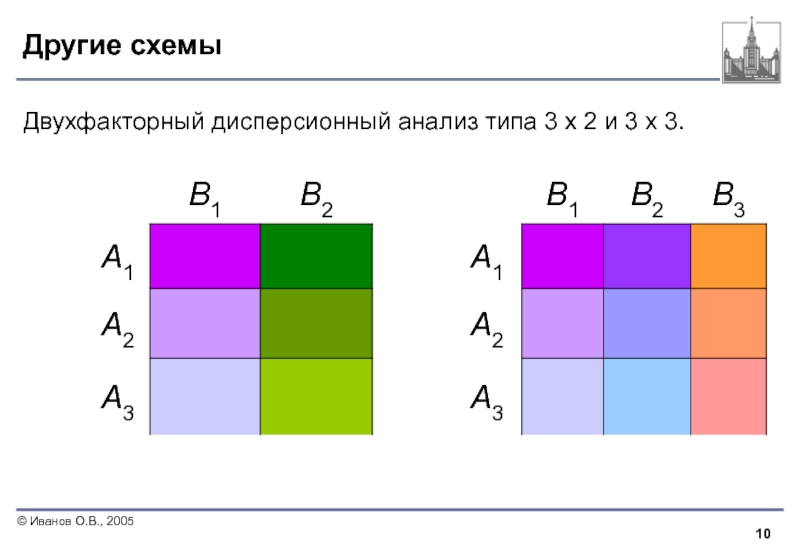
- 10. Другие схемы Двухфакторный дисперсионный анализ типа 3 х 2 и 3 х 3.
- 11. Гипотезы Схема двухфакторного дисперсионного анализа имеет несколько
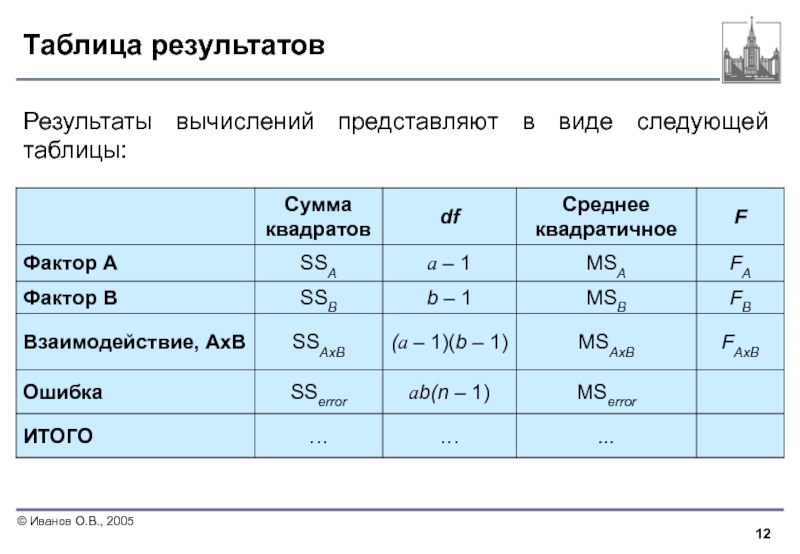
- 12. Таблица результатов Результаты вычислений представляют в виде следующей таблицы:
- 13. Обозначения SSA – сумма квадратов для фактора
- 14. Изменчивость в двухфакторном анализе Общая изменчивость
- 15. Формулы для вычислений df.N. = a –
- 16. Условия применения Генеральные совокупности, из которых извлечены
- 17. Пример Исследователь хочет выяснить, оказывают ли тип
- 18. Последовательность действий ШАГ 1. Сформулировать гипотезы.
- 19. Шаг 1. Сформулировать гипотезы Гипотезы для взаимодействия:
- 20. Шаг 2. Критические значения для F-критерия Каждая
- 21. Шаг 2. Критические значения для F-критерия Критические
- 22. Замечание Если факторы принимают различное число значений,
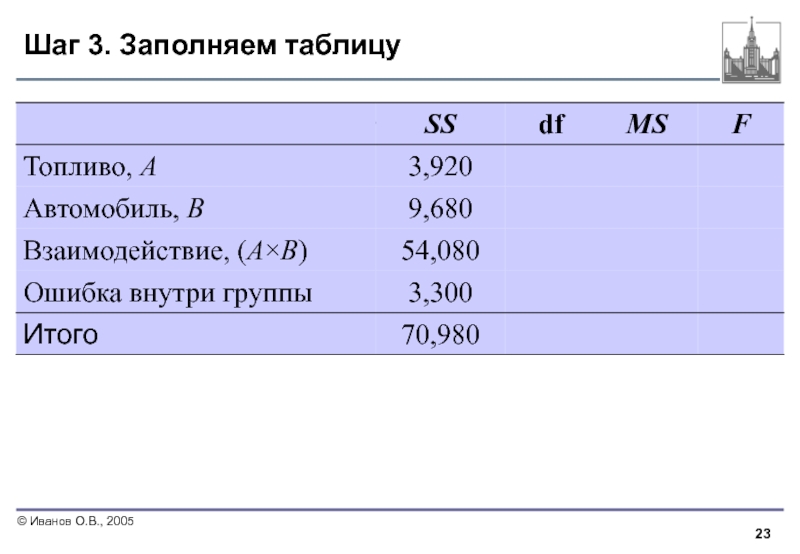
- 23. Шаг 3. Заполняем таблицу Таблица результатов вычислений
- 24. Шаг 3. Заполняем таблицу
- 25. Шаг 3. Заполняем таблицу
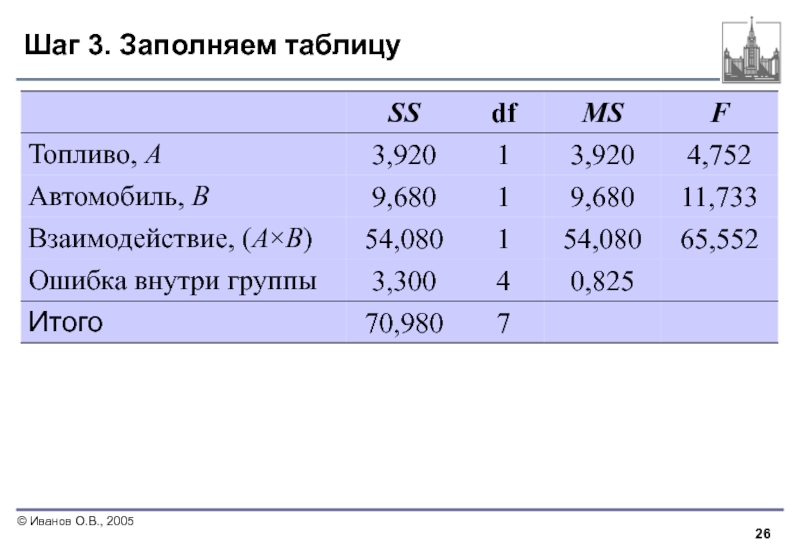
- 26. Шаг 3. Заполняем таблицу
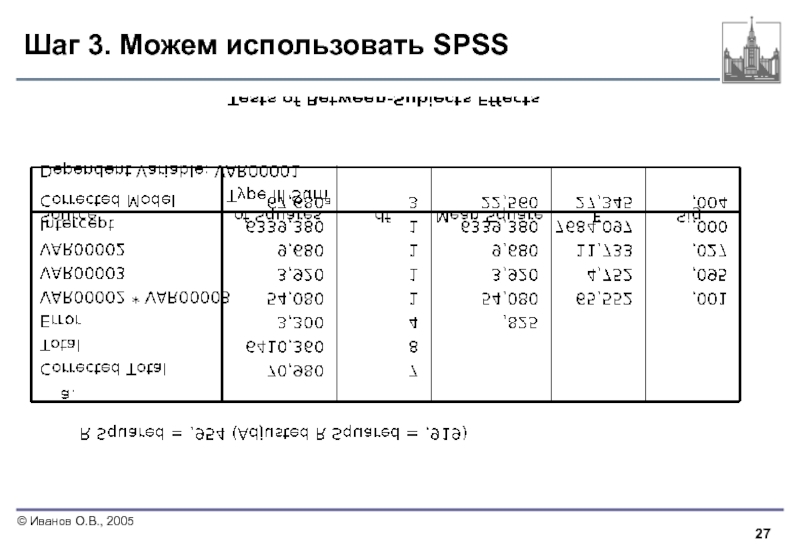
- 27. Шаг 3. Можем использовать SPSS
- 28. Шаг 4-5. Принять решение и подвести итог
- 29. Итоги Подводя итоги, можно сказать, что двумерный
- 30. 11-2. Анализ взаимодействия Метод Пример
- 31. Интерпретация результатов анализа В предыдущем примере влияние
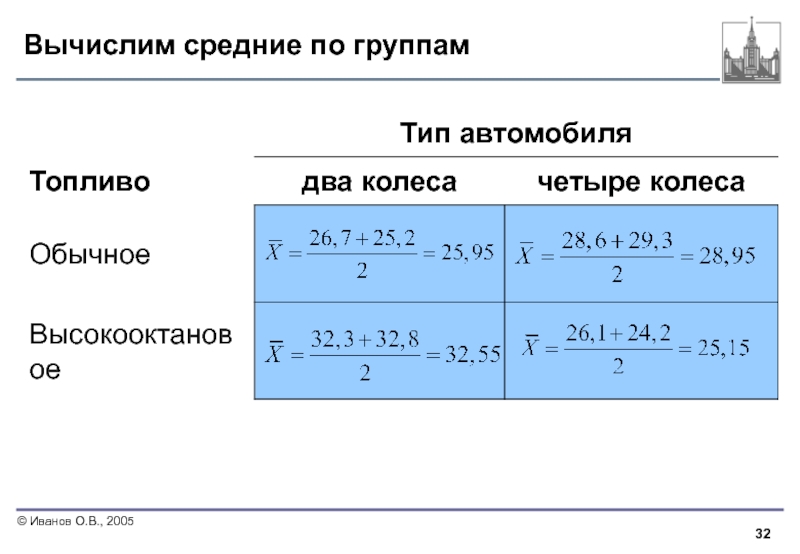
- 32. Вычислим средние по группам
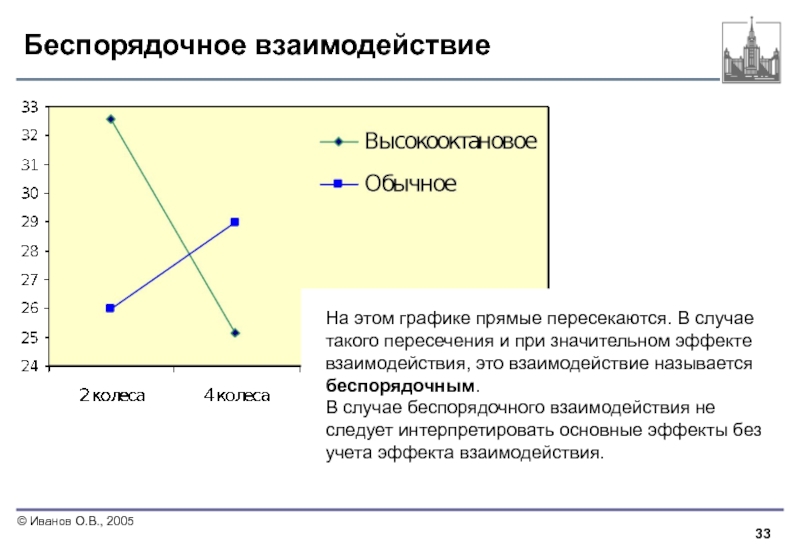
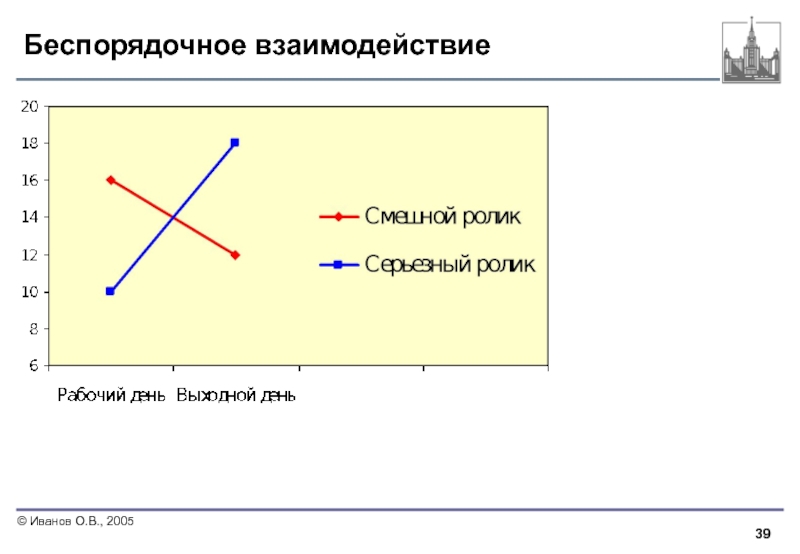
- 33. Беспорядочное взаимодействие На этом графике
- 34. Порядковое взаимодействие Другой возможный тип
- 35. Отсутствие взаимодействия Наконец, когда нет
- 36. Пример Какой вывод можно сделать из этого графика?
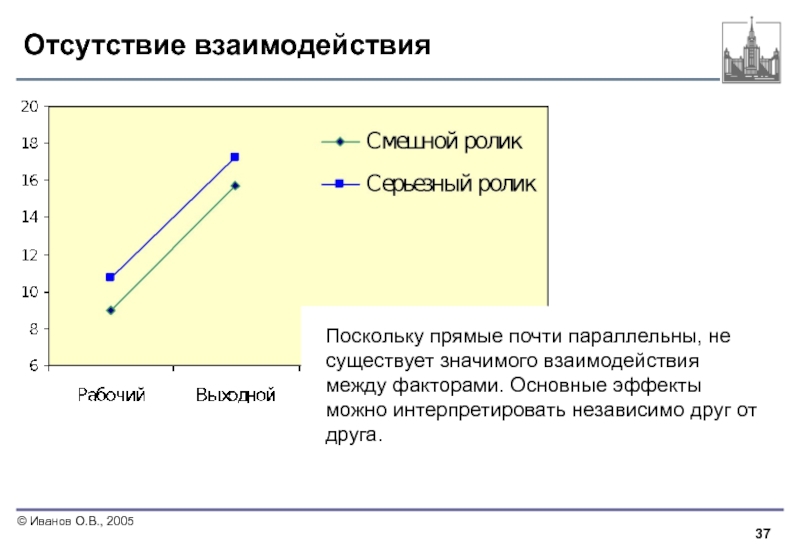
- 37. Отсутствие взаимодействия Поскольку прямые почти
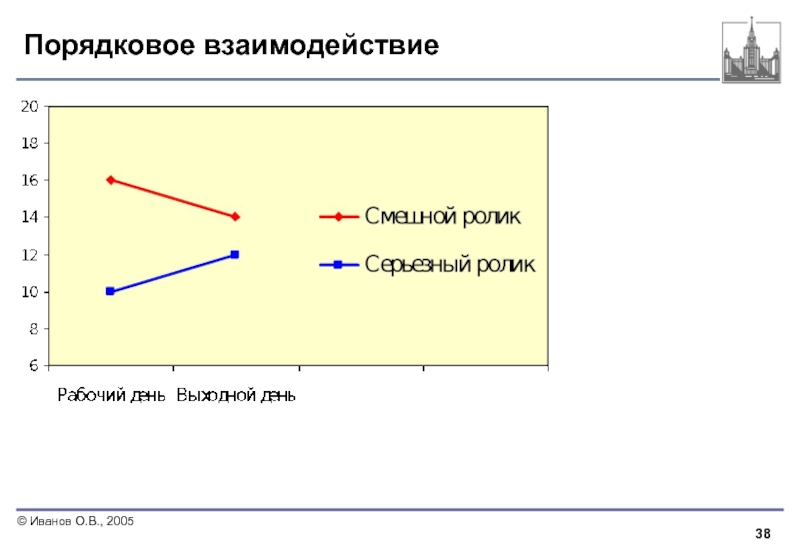
- 38. Порядковое взаимодействие
- 39. Беспорядочное взаимодействие
- 40. 11-2. Решение задачи в SPSS Ввод данных Анализ Отчет
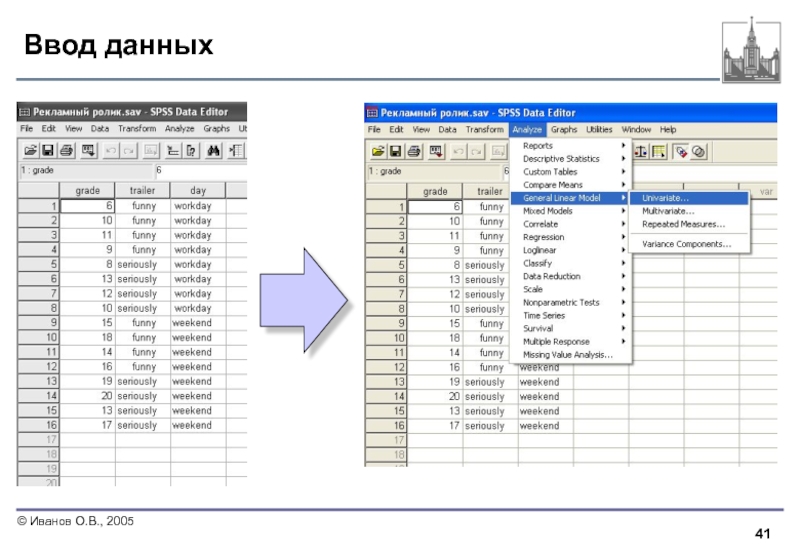
- 41. Ввод данных
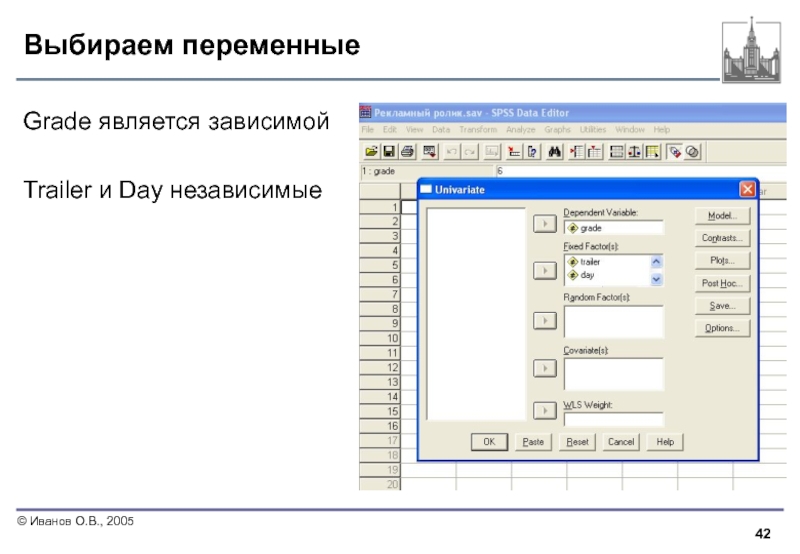
- 42. Выбираем переменные Grade является зависимой Trailer и Day независимые
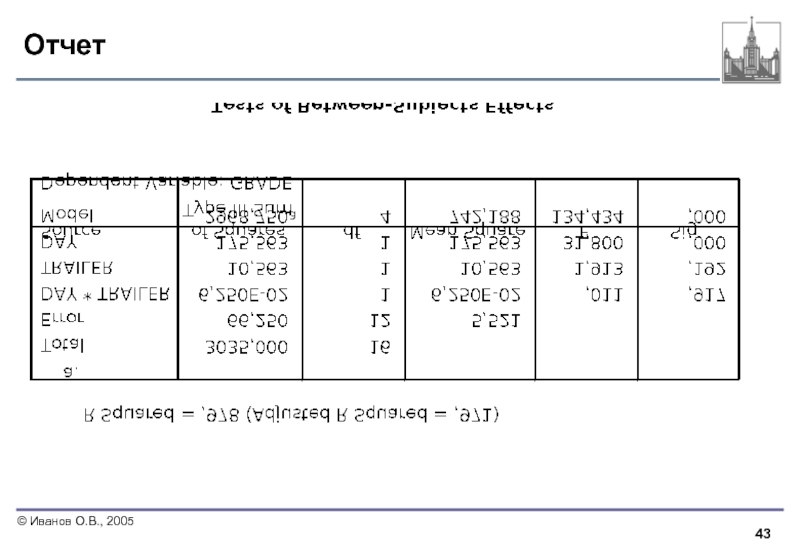
- 43. Отчет
Слайд 1Лекция 11.
Двухфакторный дисперсионный анализ
11-1. Описание метода и пример
11-2. Анализ взаимодействия
11-3.
Слайд 2Пример
Компания хочет проверить эффективность своей рекламы. Выбран продукт, и созданы два
Слайд 4Дисперсионный анализ (Analysis of Variance)
F-критерий, который мы использовали при сравнении дисперсий,
Этот метод называется дисперсионным анализом или в англоязычной аббревиатуре ANOVA (Analysis of Variance).
F-критерий можно использовать при сравнении двух средних. Но в этом случае он становится идентичным t-критерию.
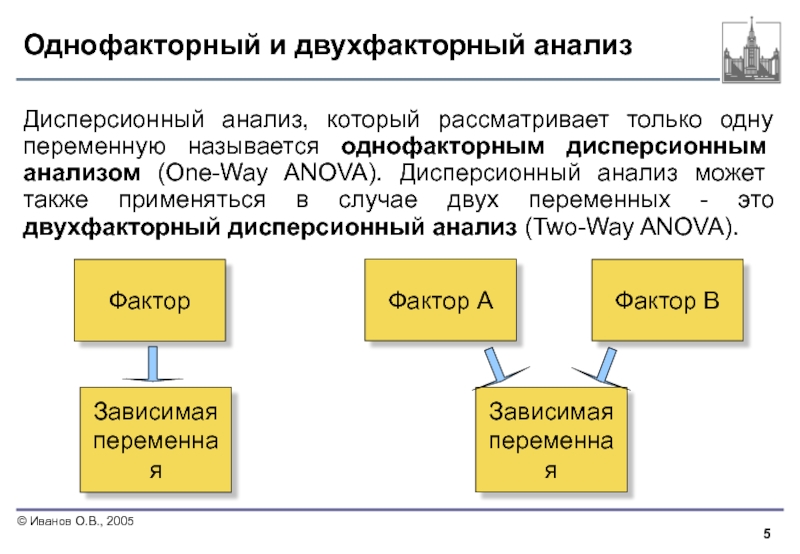
Слайд 5Однофакторный и двухфакторный анализ
Дисперсионный анализ, который рассматривает только одну переменную называется
Фактор А
Фактор B
Зависимая
переменная
Фактор
Зависимая
переменная
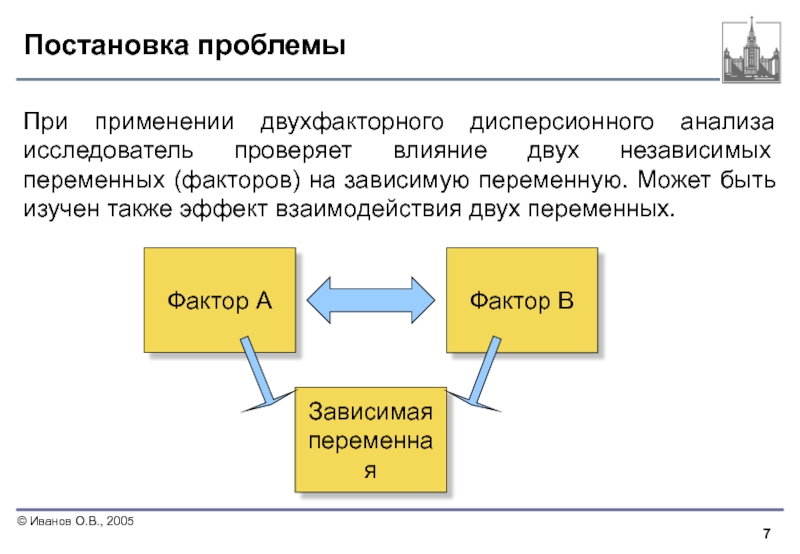
Слайд 7Постановка проблемы
При применении двухфакторного дисперсионного анализа исследователь проверяет влияние двух независимых
Фактор А
Фактор B
Зависимая
переменная
Слайд 8Эффект обработки и эффект взаимодействия
Исследуемые группы называют эффектами обработки (treatment groups):
Группа
Группа 2: Смешной ролик, выходной день
Группа 3: Серьезный ролик, рабочий день
Группа 4: Серьезный ролик, выходной день
Зрители распределяются по группам случайным образом. Эта схема 2×2, так как каждая переменная состоит из двух уровней, или двух разных вариантов обработки.
Слайд 9Эффект обработки и эффект взаимодействия
Двухфакторный дисперсионный анализ позволяет исследователю проверить эффекты
Кроме этого, исследователь может проверить также дополнительную гипотезу об эффекте взаимодействия между двумя переменными. Наличие значимого эффекта будет означать, что тип ролика по-разному влияет на эффективность рекламы, в зависимости от типа дня.
Слайд 11Гипотезы
Схема двухфакторного дисперсионного анализа имеет несколько нулевых гипотез: одна для каждой
Н0: Тип ролика и день не имеют эффекта взаимодействия на эффективность рекламы.
Н1: Тип ролика и день имеют эффект взаимодействия на эффективность рекламы.
Н0: Эффективность рекламы не зависит от типа ролика.
Н1: Эффективность рекламы зависит от типа ролика.
Н0: Эффективность рекламы не зависит от типа дня.
Н1: Эффективность рекламы зависит от типа дня.
Слайд 13Обозначения
SSA – сумма квадратов для фактора А
SSB – сумма квадратов для
SSAxB – сумма квадратов для взаимодействия факторов
SSerror – сумма квадратов для ошибки
а – количество уровней фактора А
b – количество уровней фактора В
n – количество объектов в каждой группе
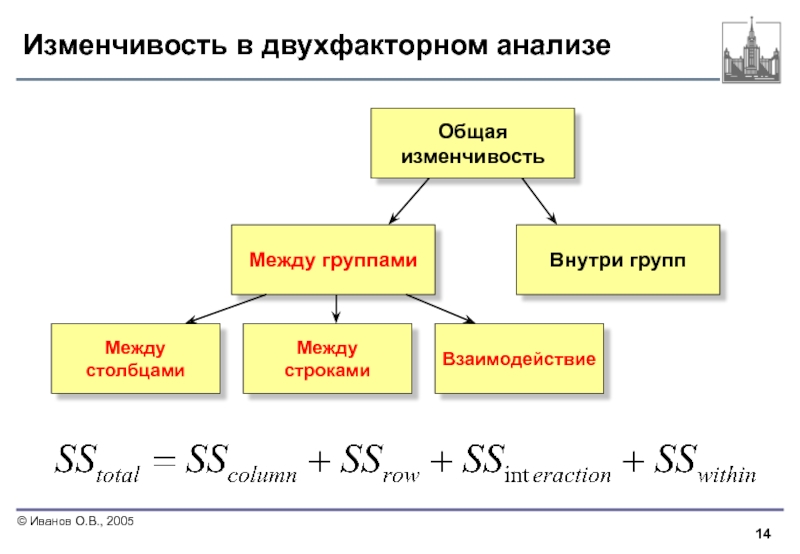
Слайд 14Изменчивость в двухфакторном анализе
Общая
изменчивость
Между группами
Внутри групп
Между
столбцами
Между
строками
Взаимодействие
Слайд 15Формулы для вычислений
df.N. = a – 1
df.D. = ab(n – 1)
df.N.
df.D. = ab(n – 1)
df.N. = (a – 1)(b – 1)
df.D. = ab(n – 1)
Слайд 16Условия применения
Генеральные совокупности, из которых извлечены выборки, должны быть нормально распределены.
Выборки
Дисперсии генеральных совокупностей, из которых извлекались выборки, должны быть равными.
Группы должны иметь одинаковый объем выборки.
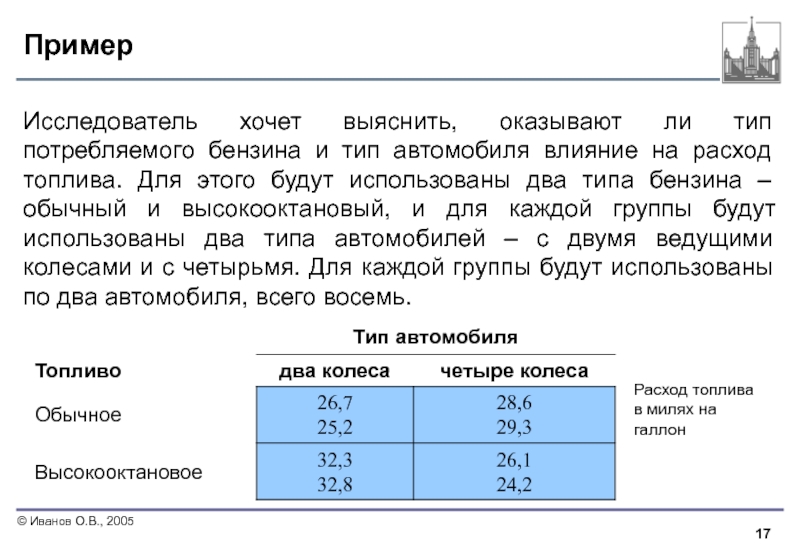
Слайд 17Пример
Исследователь хочет выяснить, оказывают ли тип потребляемого бензина и тип автомобиля
Расход топлива в милях на галлон
Слайд 18Последовательность действий
ШАГ 1. Сформулировать гипотезы.
ШАГ 2. Найти критическое значение для каждого
ШАГ 3. Заполнить итоговую таблицу, чтобы получить значение критерия.
ШАГ 4. Принять решение.
ШАГ 5. Подвести итоги.
Слайд 19Шаг 1. Сформулировать гипотезы
Гипотезы для взаимодействия:
Н0: Тип топлива и тип автомобиля
Н1: Тип топлива и тип автомобиля оказывают эффекта взаимодействия на потребление бензина.
Гипотезы для типов топлива:
Н0: Для двух типов топлива нет разницы между средним потреблением бензина. Н1: Для двух типов топлива существует разница между средним потреблением бензина.
Гипотезы для типов автомобилей:
Н0: Для автомобилей с двумя и четырьмя ведущими колесами нет разницы в среднем потреблении бензина.
Н1: Для автомобилей с двумя и четырьмя ведущими колесами существует разница в среднем потреблении бензина.
Слайд 20Шаг 2. Критические значения для F-критерия
Каждая независимая переменная, или фактор, имеет
Фактор А - тип топлива: обычное и высокооктановое, а = 2.
Фактор В - тип автомобиля: также имеет два значения, b = 2.
Степени свободы для каждого фактора:
Фактор А: df.N = a – 1 = 2 – 1 = 1
Фактор В: df.N = b – 1 = 2 – 1 = 1
Взаимодействие (A×B): df.N = (a – 1)(b – 1) = (2 – 1)(2 – 1) = 1
Ошибка внутри группы: df.D = ab(n – 1) = 2×2(2 – 1) = 4
n – число объектов в каждой группе. В данном случае n = 2.
Слайд 21Шаг 2. Критические значения для F-критерия
Критические значения:
FA α = 0,05 df.N
FВ α = 0,05 df.N = 1 df.D = 4 FВ = 7,71
FАхВ α = 0,05 df.N = 1 df.D = 4 FАхВ =7,71
Слайд 22Замечание
Если факторы принимают различное число значений, критические значения не всегда будут
Например, если фактор А имеет три значения, а фактор В – четыре, и при этом в каждой группе по два объекта, то степени свободы будут следующие:
df.N. = a – 1 = 3 – 1 = 2 для фактора А
df.N. = b – 1 = 4 – 1 = 3 для фактора В
df.N. = (a – 1)(b – 1) = (3 – 1)(4 – 1) = 6 для фактора A×B
df.D. = ab(n – 1) = 3×4(2 – 1) = 12 ошибка внутри группы
Слайд 28Шаг 4-5. Принять решение и подвести итог
Поскольку FB = 11,733 и
Итог. Поскольку нулевая гипотеза об эффекте взаимодействия была отвергнута, можно сделать вывод о том, что сочетание типа топлива и типа автомобиля оказывает существенное влияние на потребление топлива.
Слайд 29Итоги
Подводя итоги, можно сказать, что двумерный дисперсионный анализ является продолжением одномерного.
Слайд 31Интерпретация результатов анализа
В предыдущем примере влияние типа бензина и типа автомобиля
Однако, если существует значимый эффект взаимодействия, надо более внимательно интерпретировать основные эффекты. Чтобы интерпретировать результаты двумерного дисперсионного анализа, исследователи предлагают нарисовать график, на который наносятся средние значения каждой группы. Затем проанализировать график и интерпретировать результаты.
Слайд 33Беспорядочное взаимодействие
На этом графике прямые пересекаются. В случае такого пересечения и
В случае беспорядочного взаимодействия не следует интерпретировать основные эффекты без учета эффекта взаимодействия.
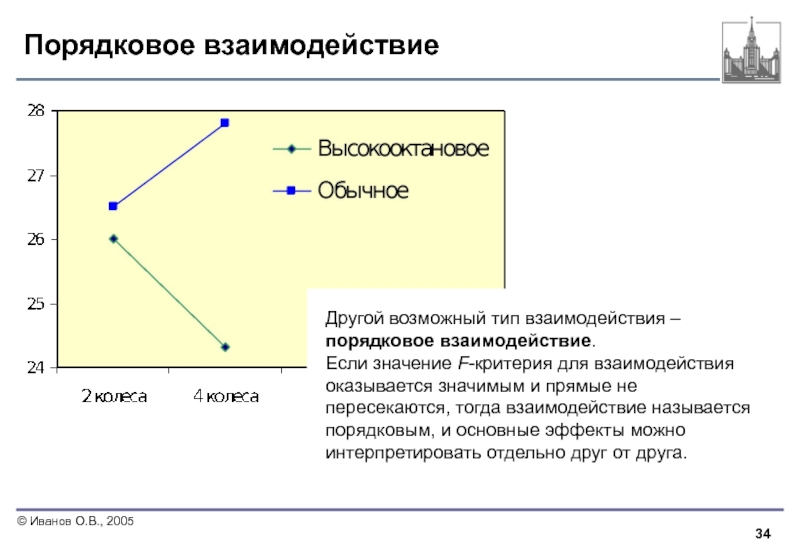
Слайд 34Порядковое взаимодействие
Другой возможный тип взаимодействия – порядковое взаимодействие.
Если значение F-критерия
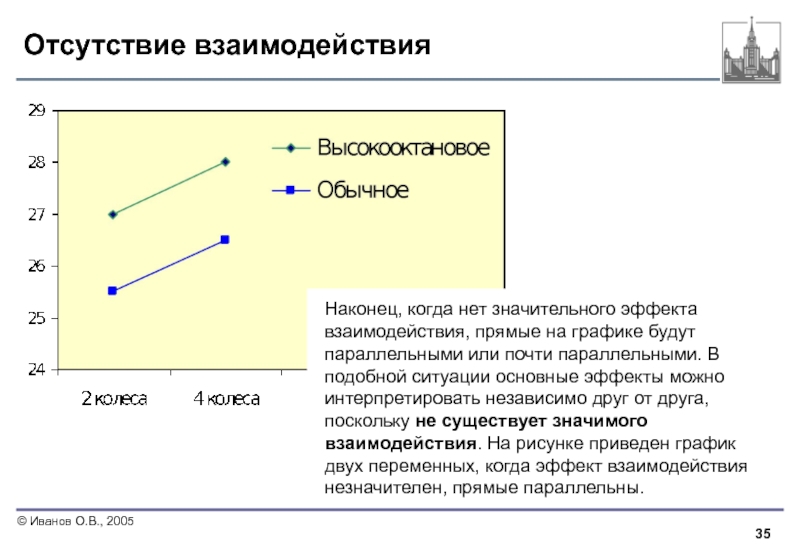
Слайд 35Отсутствие взаимодействия
Наконец, когда нет значительного эффекта взаимодействия, прямые на графике будут