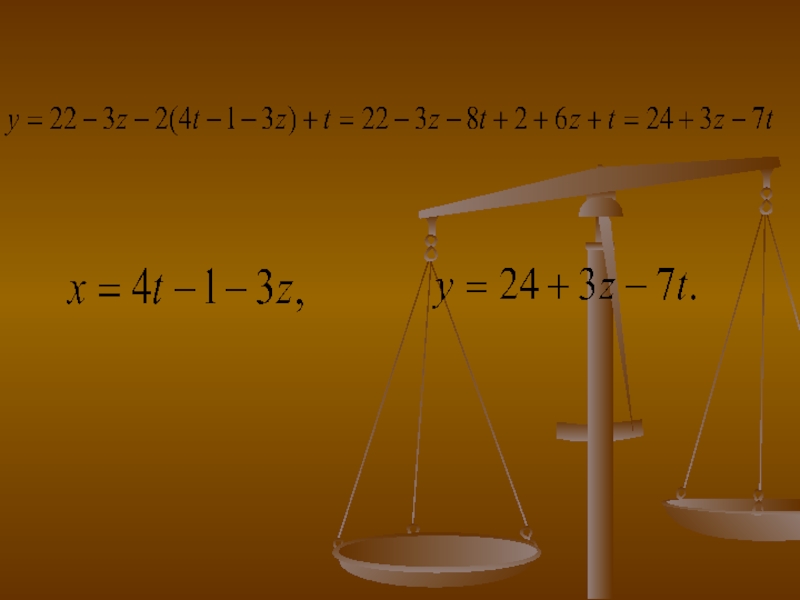Диофант и неопределенные уравнения презентация

Содержание

1. Диофант и неопределенные уравнения
2. При выполнении работы были поставлены следующие
3. Прах Диофанта гробница покоит: дивись ей –
4. Пусть Диофант прожил x лет. Составим и
5. Неопределенные уравнения первой степени 1.) ax +
6. Метод перебора Метод «спуска» Неопределенные уравнения первой
7. Метод перебора Рассмотрим и решим уравнение: 4,5х+6у=57
8. Таким образом, подставляя вместо х
9. Метод спуска 1) Если свободный член с
10. Рассмотрим задачу: Покупатель приобрел в магазине на
11. По условию x > 0, y >
12. Неопределенные уравнения первой степени вида ax
13. Решение:
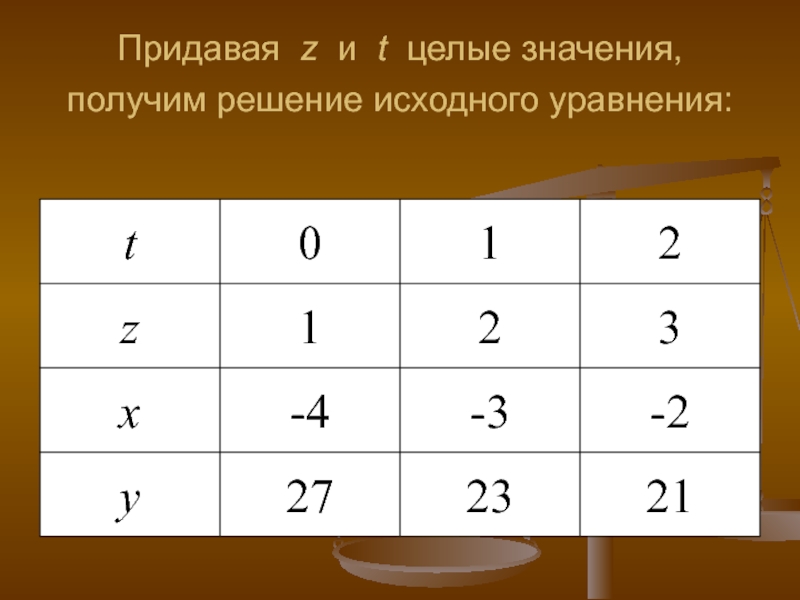
15. Придавая z и t целые значения, получим решение исходного уравнения:
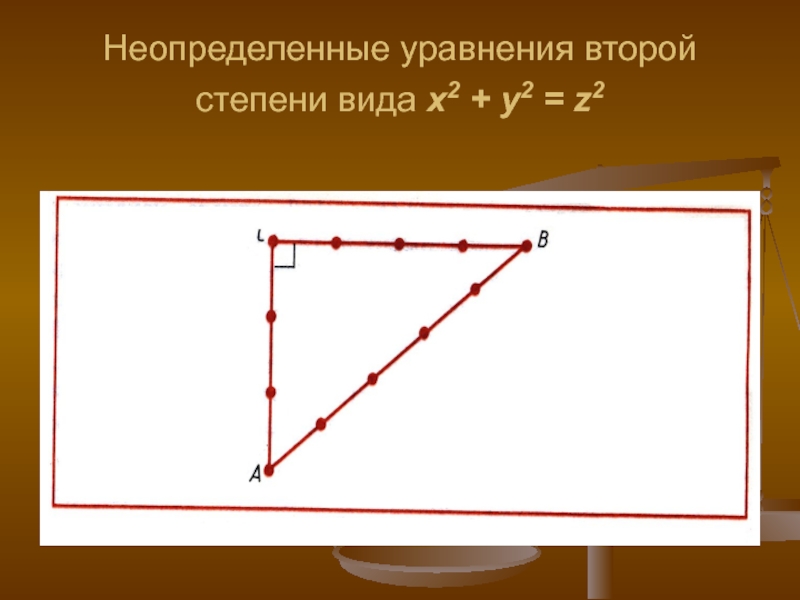
16. Неопределенные уравнения второй степени вида x2 + y2 = z2
17. Один из путей решения уравнения в целых
18. Сформулируем такую теорему:
19. Числа, найденные по такому
20. Заключение Диофантовы уравнения и их решения и

При выполнении работы были поставлены следующие задачи: расширить свой кругозор знаний по математике; рассмотреть некоторые методы решения неопределенных уравнений; показать практическое применение неопределенных уравнений.

Главная
Математика
Диофант и неопределенные уравнения

Слайд 1Диофант и неопределенные уравнения

Слайд 2 При выполнении работы были поставлены следующие задачи:
расширить свой кругозор знаний

по математике;
рассмотреть некоторые методы решения неопределенных уравнений;
показать практическое применение неопределенных уравнений.

Слайд 3Прах Диофанта гробница покоит: дивись ей – и камень
Мудрым искусством его

скажет усопшего век.
Волей богов шестую часть жизни он прожил ребенком
И половину шестой встретил с пушком на щеках.
Только минула седьмая, с подругою он обручился.
С нею пять лет проведя, сына дождался мудрец.
Только полжизни отцовской возлюбленный сын его
прожил.
Отнят он был у отца ранней могилой своей.
Дважды два года родитель оплакивал тяжкое горе.
Тут и увидел предел жизни печальной своей.

Слайд 4Пусть Диофант прожил x лет. Составим и решим уравнение:
Умножим уравнение

на 84, чтобы избавиться от дробей:

Слайд 5Неопределенные уравнения первой степени
1.) ax + by = с
2.) ax

+ by + cz = d

Слайд 6Метод перебора
Метод «спуска»
Неопределенные уравнения первой степени вида ax + by

= c

Слайд 7Метод перебора Рассмотрим и решим уравнение: 4,5х+6у=57 Нужно найти все натуральные значения переменных х

и у

Решение. Помножим обе части уравнения на 2, чтобы избавиться от дробных чисел, получим:
9х+12у=114
Выразим у через х:
У= 114 – 9х
12
Далее воспользуемся методом перебора
(учитывая, что х и у - натуральные):

Слайд 8 Таким образом, подставляя вместо х числа, удовлетворяющие равенству, получили

некоторые значения у .

Слайд 9Метод спуска
1) Если свободный член с неопределенного уравнения ax + by

= c не делится на НОД (a, b), то уравнение не имеет целых корней.

2) Если коэффициенты a, b являются взаимно простыми числами, то уравнение имеет, по крайней мере, одно целое решение.

Слайд 10Рассмотрим задачу: Покупатель приобрел в магазине на 21 р. товара. Но у

него в наличии денежные знаки только 5 – рублевого достоинства, а у кассира – 3-рублевого. Требуется знать , можно ли при наличии денег расплатиться с кассиром и как именно?

Решение: x – число 5 - рублевок, y – 3 - рублевок.

Слайд 11По условию x > 0, y > 0, значит
Кроме

того, t – четное, иначе ни x, ни y не будут
целыми.
При t = 4, 6, 8, … имеем:

Подставим в у вместо х дробь 3/2t

Слайд 12Неопределенные уравнения первой степени вида ax + by + cz= d.

Рассмотрим уравнение:

Нужно найти любые целые решения уравнения.

Слайд 13

Решение:

Слайд 14

Слайд 15Придавая z и t целые значения, получим решение исходного уравнения:

Слайд 16Неопределенные уравнения второй степени вида x2 + y2 = z2

Слайд 17Один из путей решения уравнения в целых числах оказался довольно простым.

Запишем подряд квадраты натуральных чисел, отделив их друг от друга запятой. Под каждой запятой запишем разность между последовательными квадратами:

1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196…
3, 5, 7, 9, 11, 13, 15, 17, 19 , 21, 23, 25, 27…

Слайд 18Сформулируем такую теорему: Каждое нечетное число есть

разность двух последовательных квадратов

если х - нечетное число, то

Слайд 19

Числа, найденные по такому правилу, всегда будут составлять решение интересующего

нас неопределенного уравнения. Это уравнение будем называть «уравнением Пифагора», а его решения – «пифагоровыми тройками». По этому правилу можно получить уже известные нам тройки:

Слайд 20Заключение
Диофантовы уравнения и их решения и по сей день остаются актуальной

темой.
Умение решать такие уравнения позволяет найти остроумные и сравнительно простые решения казалось бы «неразрешимых» задач, а в практической деятельности значительно сэкономить затраты средств и времени.
Проведя данное исследование, я овладела новыми математическими навыками, рассмотрела некоторые методы решения неопределенных уравнений.
Изучая диофантовы уравнения, показала практическое им применение, решив несколько задач.

Скачать презентацию

Диофант и неопределенные уравнения презентация

Содержание

Слайд 1Диофант и неопределенные уравнения

Слайд 2 При выполнении работы были поставлены следующие задачи:
расширить свой кругозор знаний

Слайд 3Прах Диофанта гробница покоит: дивись ей – и камень
Мудрым искусством его

Слайд 4Пусть Диофант прожил x лет. Составим и решим уравнение:
Умножим уравнение

Слайд 5Неопределенные уравнения первой степени
1.) ax + by = с
2.) ax

Слайд 6Метод перебора
Метод «спуска»
Неопределенные уравнения первой степени вида ax + by

Слайд 7Метод перебора Рассмотрим и решим уравнение: 4,5х+6у=57 Нужно найти все натуральные значения переменных х

Слайд 8 Таким образом, подставляя вместо х числа, удовлетворяющие равенству, получили

Слайд 9Метод спуска
1) Если свободный член с неопределенного уравнения ax + by

Слайд 10Рассмотрим задачу: Покупатель приобрел в магазине на 21 р. товара. Но у

Слайд 11По условию x > 0, y > 0, значит
Кроме

Слайд 12Неопределенные уравнения первой степени вида ax + by + cz= d.

Слайд 13

Решение:

Слайд 14

Слайд 15Придавая z и t целые значения, получим решение исходного уравнения:

Слайд 16Неопределенные уравнения второй степени вида x2 + y2 = z2

Слайд 17Один из путей решения уравнения в целых числах оказался довольно простым.

Слайд 18Сформулируем такую теорему: Каждое нечетное число есть

Слайд 19

Числа, найденные по такому правилу, всегда будут составлять решение интересующего

Слайд 20Заключение
Диофантовы уравнения и их решения и по сей день остаются актуальной

Обратная связь

Что такое ThePresentation.ru?

Диофант и неопределенные уравнения презентация

Содержание

Слайд 1Диофант и неопределенные уравнения

Слайд 2 При выполнении работы были поставлены следующие задачи:расширить свой кругозор знаний

Слайд 3Прах Диофанта гробница покоит: дивись ей – и каменьМудрым искусством его

Слайд 4Пусть Диофант прожил x лет. Составим и решим уравнение: Умножим уравнение

Слайд 5Неопределенные уравнения первой степени1.) ax + by = с 2.) ax

Слайд 6Метод перебораМетод «спуска»Неопределенные уравнения первой степени вида ax + by

Слайд 7Метод перебора Рассмотрим и решим уравнение: 4,5х+6у=57 Нужно найти все натуральные значения переменных х

Слайд 8 Таким образом, подставляя вместо х числа, удовлетворяющие равенству, получили

Слайд 9Метод спуска1) Если свободный член с неопределенного уравнения ax + by

Слайд 10Рассмотрим задачу: Покупатель приобрел в магазине на 21 р. товара. Но у

Слайд 11По условию x > 0, y > 0, значит Кроме

Слайд 12Неопределенные уравнения первой степени вида ax + by + cz= d.

Слайд 13Решение:

Слайд 14

Слайд 15Придавая z и t целые значения, получим решение исходного уравнения:

Слайд 16Неопределенные уравнения второй степени вида x2 + y2 = z2

Слайд 17Один из путей решения уравнения в целых числах оказался довольно простым.

Слайд 18Сформулируем такую теорему: Каждое нечетное число есть

Слайд 19 Числа, найденные по такому правилу, всегда будут составлять решение интересующего

Слайд 20ЗаключениеДиофантовы уравнения и их решения и по сей день остаются актуальной

Похожие презентации

Обратная связь

Что такое ThePresentation.ru?

Слайд 2 При выполнении работы были поставлены следующие задачи:
расширить свой кругозор знаний

Слайд 3Прах Диофанта гробница покоит: дивись ей – и камень
Мудрым искусством его

Слайд 4Пусть Диофант прожил x лет. Составим и решим уравнение:
Умножим уравнение

Слайд 5Неопределенные уравнения первой степени
1.) ax + by = с
2.) ax

Слайд 6Метод перебора
Метод «спуска»
Неопределенные уравнения первой степени вида ax + by

Слайд 9Метод спуска
1) Если свободный член с неопределенного уравнения ax + by

Слайд 11По условию x > 0, y > 0, значит
Кроме

Слайд 13

Решение:

Слайд 19

Числа, найденные по такому правилу, всегда будут составлять решение интересующего

Слайд 20Заключение
Диофантовы уравнения и их решения и по сей день остаются актуальной