и только тогда, когда существует ее производная в этой точке. При этом выражение
есть дифференциал функции.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дифференцирование функции презентация
Содержание
- 1. Дифференцирование функции
- 2.
- 3.
- 4.
- 5. Геометрический смысл производной Значение производной f '(x0)
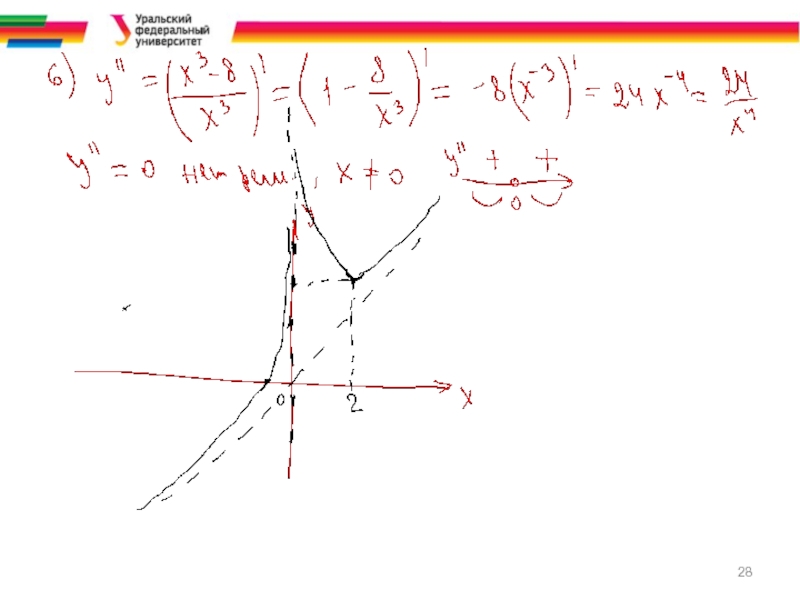
- 6. Пример. Составить уравнения нормали к линии
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17. §5. Исследование функции Проводится по следующей схеме
- 18. f(х) – периодическая с периодом Т ⇔
- 19.
- 20.
- 21.
- 22.
- 23.
- 24. По результатам исследования строят график функции и при необходимости находят 7.* Дополнительные точки.
- 25.
- 30.
Геометрический смысл производной Значение производной f '(x0) равно угловому коэффициенту касательной, проведенной к кривой y = f '(x) в точке M0(x0, f(x0)): f '(x0) = kкас. Уравнение касательной, проходящим
Слайд 1§4. Дифференцирование функции
Определение производной
Функция f(x) дифференцируема в точке x тогда
Слайд 5Геометрический смысл производной
Значение производной f '(x0) равно угловому коэффициенту касательной, проведенной
к кривой
y = f '(x) в точке M0(x0, f(x0)): f '(x0) = kкас.
Уравнение касательной, проходящим через точку M0, имеет вид: y − y0 = f '(x0) (x − x0).
Нормаль – прямая, проходящая через точку касания перпендикулярно касательной. Тогда kнорм = − 1/kкас.
Уравнение нормали: y − y0 = (− 1/f '(x0))·(x − x0).
y = f '(x) в точке M0(x0, f(x0)): f '(x0) = kкас.
Уравнение касательной, проходящим через точку M0, имеет вид: y − y0 = f '(x0) (x − x0).
Нормаль – прямая, проходящая через точку касания перпендикулярно касательной. Тогда kнорм = − 1/kкас.
Уравнение нормали: y − y0 = (− 1/f '(x0))·(x − x0).
Слайд 6Пример. Составить уравнения нормали к линии
y = x3+ 3x2 −
5, параллельной прямой 2х − 6у + 1 = 0.
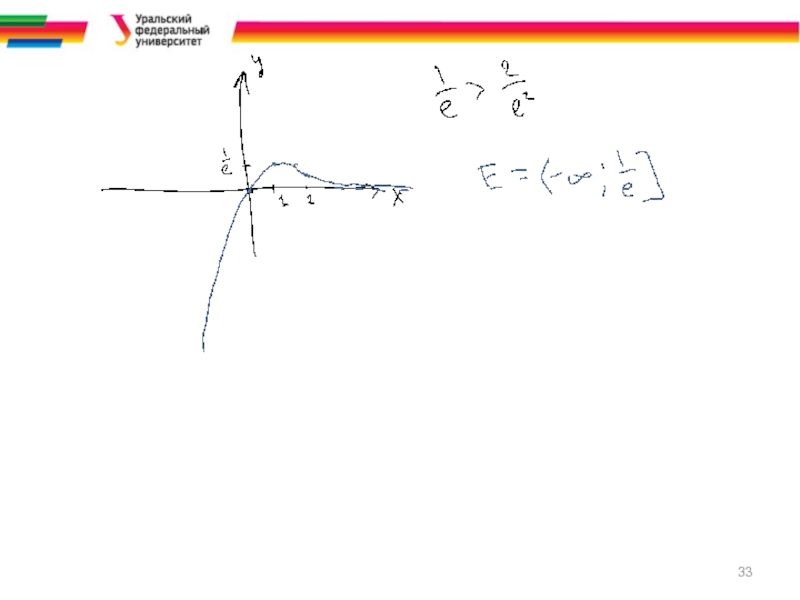
Слайд 17§5. Исследование функции
Проводится по следующей схеме
1. Область определения функции D(f).
Множество значений функции E(f).
2. Четность, нечетность, периодичность
f(х) – четная ⇔ ∀х, (−х)∈D(f) f(− х) = f(х)
(график симметричен относительно оси Оу)
f(х) – нечетная ⇔ ∀х, (−х)∈D(f) f(− х) = − f(х)
(график симметричен относительно начала координат)
Если ни одно условие не выполняется, то
f(х) – функция общего вида.
2. Четность, нечетность, периодичность
f(х) – четная ⇔ ∀х, (−х)∈D(f) f(− х) = f(х)
(график симметричен относительно оси Оу)
f(х) – нечетная ⇔ ∀х, (−х)∈D(f) f(− х) = − f(х)
(график симметричен относительно начала координат)
Если ни одно условие не выполняется, то
f(х) – функция общего вида.
Слайд 18f(х) – периодическая с периодом Т ⇔
∀х, (х−Т), (х+Т) ∈D(f)
f(х) = f(х−Т) = f(х+Т)
(определяется только для тригонометрических функций)
3. Точки пересечения графика с осями координат
Пересечение с Оу существует, если х = 0 ∈D(f), точка пересечения (0, f(0))
(график пересекает Оу не более чем в одной точке).
Пересечение с Ох определяется в результате решения уравнения: f(х) = 0.
(определяется только для тригонометрических функций)
3. Точки пересечения графика с осями координат
Пересечение с Оу существует, если х = 0 ∈D(f), точка пересечения (0, f(0))
(график пересекает Оу не более чем в одной точке).
Пересечение с Ох определяется в результате решения уравнения: f(х) = 0.
Слайд 24По результатам исследования строят график функции и при необходимости находят
7.* Дополнительные
точки.
