- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дифференциальное исчисление (продолжение) презентация
Содержание
- 1. Дифференциальное исчисление (продолжение)
- 2. Производная Общая схема исследования функций
- 3. Производная Чтобы найти экстремумы
- 4. Производная Чтобы найти точку пересечения
- 5. Задача Пример. Исследовать функцию и построить её график
- 6. Задача Пример. Исследовать функцию и
- 7. Задача Ищем наклонные асимптоты:
- 8. Задача Ищем точки перегиба функции:
- 9. Задача Ищем точки пересечения с осями координат:
- 10. Задача
- 11. Задача
- 12. Задача Пример. Исследовать функцию и построить её
- 13. Задача Вертикальные асимптоты могут проходить через точки
- 14. Задача Наклонные асимптоты:
- 15. Задача Экстремумы:
- 16. Задача 6. Ищем точки перегиба функции:
- 17. Задача 6. (0; 0) – единственная точка
- 18. Задача
- 19. Задача
- 20. Задача Пример. Исследовать функцию и построить её график
- 21. Задача Пример. Исследовать функцию и построить её
- 22. Задача 4. Ищем наклонные асимптоты:
- 23. Задача Таким образом получили y = 0
- 24. Задача Ищем точки перегиба функции:
- 25. Задача Ищем точки пересечения с осью абсцисс
- 26. Задача
- 27. Задача
- 28. Задача Пример. Исследовать функцию и построить её График
- 29. Задача Пример. Исследовать функцию и построить её
- 30. Задача Т.о. вертикальных асимптот
- 31. Задача Ищем точки перегиба функции:
- 32. Задача Ищем точки пересечения с осью абсцисс:
- 33. Задача
- 34. Задача
- 35. Финансовый университет при Правительстве Российской Федерации Тема №5. Дифференциал функции
- 36. Дифференциал функции Дифференциалом функции в
- 37. Задача Найдём дифференциал функции y(x)=x
- 38. Дифференциал функции
- 39. Дифференциал функции Геометрический смысл дифференциала
- 40. Дифференциал функции Нахождение дифференциала
- 41. Задача Пример. Вычислить приближённо синус
- 42. Финансовый университет при Правительстве Российской Федерации Конец темы
Производная Общая схема исследования функций и построения их графиков: ООФ; Чётность – нечётность; Периодичность; Вертикальные асимптоты; Наклонные асимптоты; Экстремумы, интервалы монотонности функции; Точки перегиба, интервалы выпуклости и вогнутости функции;
Слайд 1Финансовый университет
при Правительстве Российской Федерации
Тема №4
(продолжение).
Дифференциальное исчисление
Слайд 2Производная
Общая схема исследования функций и построения их графиков:
ООФ;
Чётность –
нечётность;
Периодичность;
Вертикальные асимптоты;
Наклонные асимптоты;
Экстремумы, интервалы монотонности функции;
Точки перегиба, интервалы выпуклости и вогнутости функции;
Точки пересечения графика с осями координат, дополнительные точки функции.
Периодичность;
Вертикальные асимптоты;
Наклонные асимптоты;
Экстремумы, интервалы монотонности функции;
Точки перегиба, интервалы выпуклости и вогнутости функции;
Точки пересечения графика с осями координат, дополнительные точки функции.
Слайд 3Производная
Чтобы найти экстремумы функции следует:
Найти производную функции:
Найти критические
точки функции (приравнять к нулю и числитель, и знаменатель производной):
Нанести критические точки на числовую прямую, выяснить знак производной на каждом из полученных на прямой интервале (применив метод интервалов).
Нанести критические точки на числовую прямую, выяснить знак производной на каждом из полученных на прямой интервале (применив метод интервалов).
Слайд 4Производная
Чтобы найти точку пересечения графика функции с осью ординат
следует задать х=0.
Чтобы найти точки пересечения графика с осью абсцисс следует решить уравнение
Чтобы найти точки пересечения графика с осью абсцисс следует решить уравнение
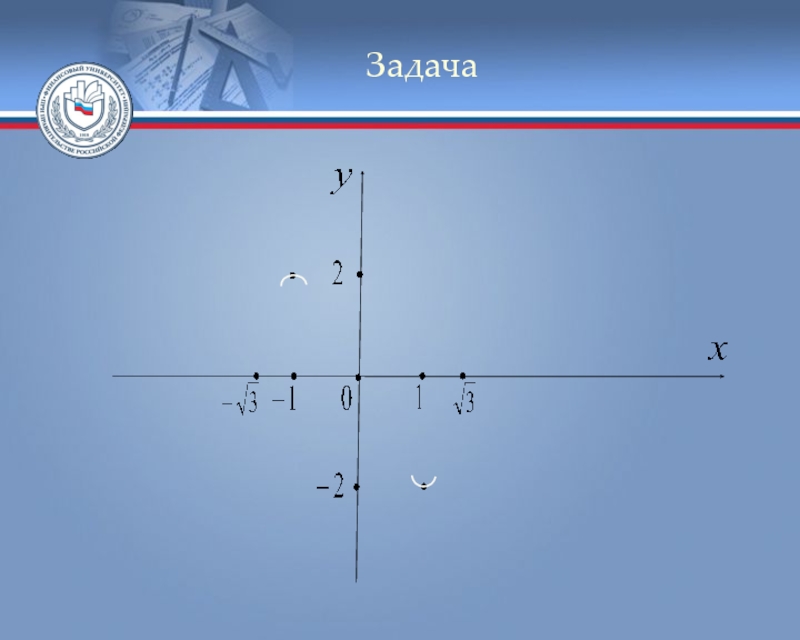
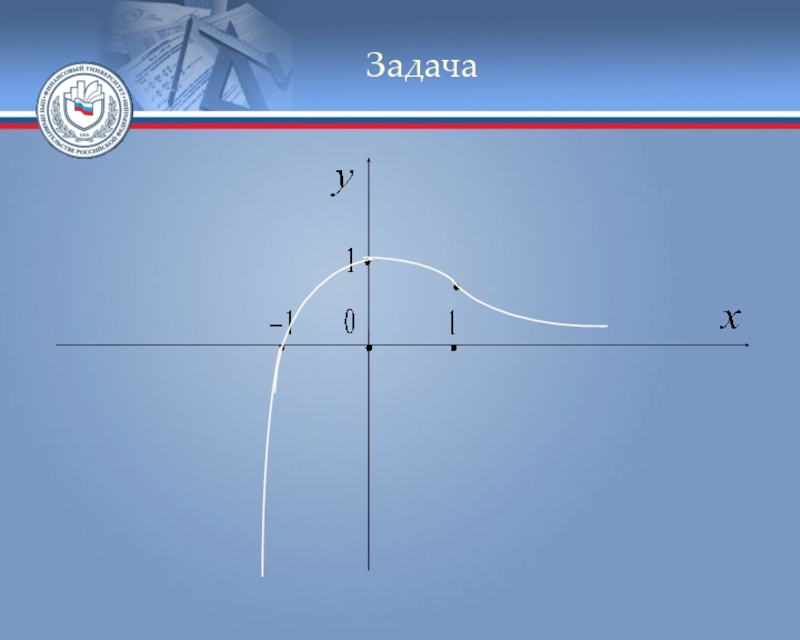
Слайд 6Задача
Пример. Исследовать функцию и построить её график
Решение:
ООФ:
Функция
нечётная, т.к.
Вертикальных асимптот нет, т.к. по ООФ х – любое.
Вертикальных асимптот нет, т.к. по ООФ х – любое.
Слайд 7Задача
Ищем наклонные асимптоты:
Следовательно наклонных асимптот нет.
5.
Ищем экстремумы функции:
Слайд 13Задача
Вертикальные асимптоты могут проходить через точки х = -1 и х
= 1. Рассмотрим односторонние пределы:
Таким образом х = -1 и х = 1 – уравнения вертикальных асимптот.
Таким образом х = -1 и х = 1 – уравнения вертикальных асимптот.
Слайд 17Задача
6. (0; 0) – единственная точка пересечения с осями координат. Для
уточнения графика можно произвольно взять любые точки, например х = 3 и х = -3.
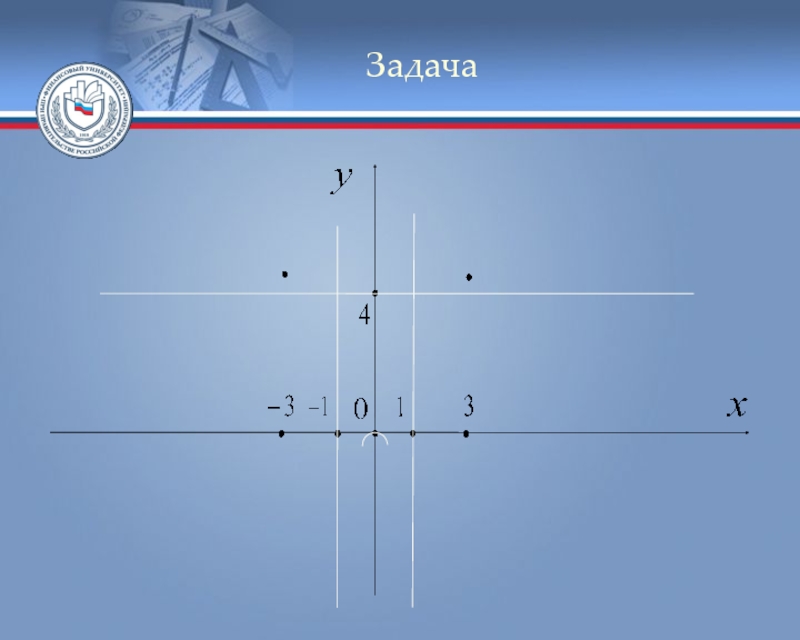
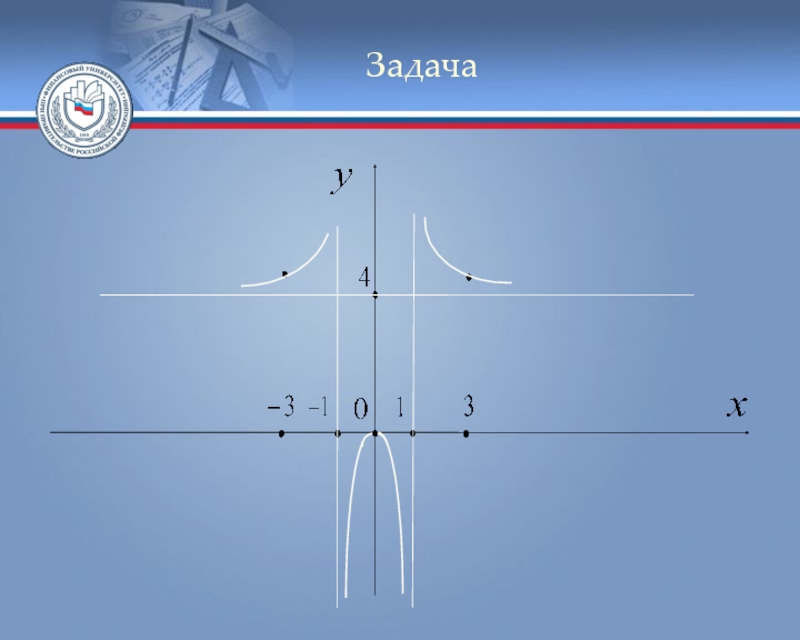
Слайд 21Задача
Пример. Исследовать функцию и построить её
график
Решение:
ООФ:
Функция общего вида, т.к.
Вертикальных
асимптот нет
Слайд 23Задача
Таким образом получили y = 0 – уравнение правосторонней горизонтальной асимптоты.
5.
Ищем экстремумы функции:
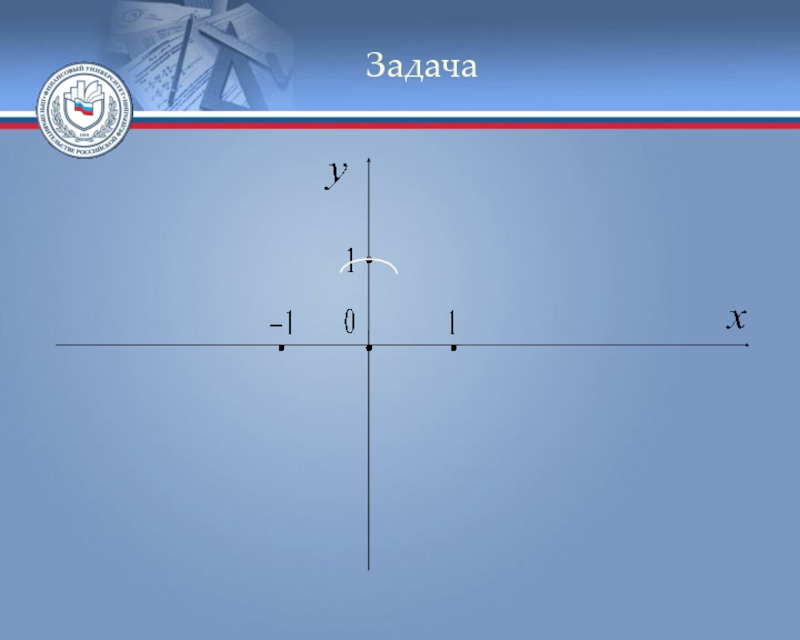
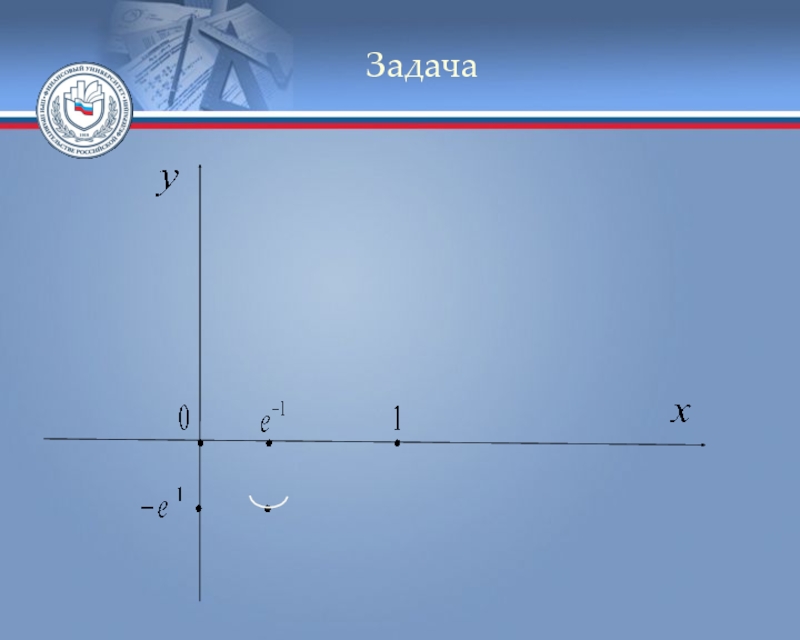
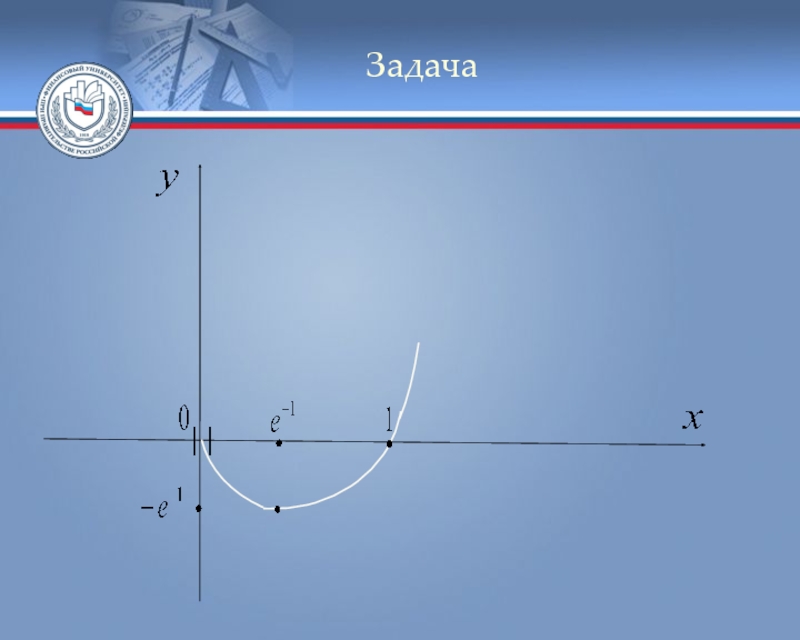
Слайд 29Задача
Пример. Исследовать функцию и построить её
График
Решение:
ООФ х > 0
Функция общего
вида
Ищем вертикальные асимптоты:
Ищем вертикальные асимптоты:
Слайд 30Задача
Т.о. вертикальных асимптот график не имеет.
4. Ищем наклонные
асимптоты:
Следовательно, наклонных асимптот у графика тоже нет.
5. Ищем экстремумы функции:
Следовательно, наклонных асимптот у графика тоже нет.
5. Ищем экстремумы функции:
Слайд 36Дифференциал функции
Дифференциалом функции в точке называется главная, линейная относительно
приращения аргумента часть приращения функции, равная произведению производной функции на приращение её аргумента
Слайд 37Задача
Найдём дифференциал функции y(x)=x :
По определению
Получили, что
дифференциал независимой переменной равен приращению этой переменной.
Следовательно
Следовательно
Слайд 39Дифференциал функции
Геометрический смысл дифференциала функции в точке: Дифференциал функции
в точке численно равен приращению ординаты касательной, проведённой к графику функции в этой точке, при изменении абсциссы этой точки на соответствующее приращение.
Свойства дифференциала функции аналогичны свойствам производной.
Свойства дифференциала функции аналогичны свойствам производной.
Слайд 40Дифференциал функции
Нахождение дифференциала от дифференциала ведёт к нахождению
дифференциала высших порядков (от второго порядка и выше).
