- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дифференциальное исчисление презентация
Содержание
- 1. Дифференциальное исчисление
- 2. Производной функции в точке называется предел, если
- 3. Производная
- 4. Производная Геометрический смысл производной функции:
- 5. Производная Нахождение
- 6. Теорема (Необходимое условие дифференцируемости функции):
- 7. Правила дифференцирования Пусть С - постоянная величина,
- 8. Формулы дифференцирования
- 9. Формулы дифференцирования
- 10. Производная Производная сложной функции
- 11. Задача Пример. Найти производную функции
- 12. Задача Пример. Найти производную функции Ответ:
- 13. Задача Пример. Найти производную функции
- 14. Задача Пример. Найти производную функции Ответ:
- 15. Задача Пример. Найти производную функции
- 16. Задача Ответ:
- 17. Задача Написать уравнение касательной к
- 18. Задача Решение:
- 19. Задача Написать уравнение касательной к
- 20. Эластичностью функции называется предел отношения
- 21. Эластичность Из определения вытекает формула расчёта эластичности функции:
- 22. Эластичность Эластичность функции приближённо показывает
- 23. Свойства эластичности Эластичность функции равна произведению независимой
- 24. Свойства эластичности 3. Эластичности взаимно обратных функции
- 25. Задача Пример. Зависимость между себестоимостью единицы продукции
- 26. Задача Решение:
- 27. Производная Основные теоремы дифференциального исчисления:
- 28. Производная 2. Теорема Ролля. Пусть функция непрерывна
- 29. Производная 3. Теорема Лагранжа. Пусть функция непрерывна
- 30. Производная 4. Теорема Ферма. Пусть функции непрерывны
- 31. Правило Лопиталя Применяется при вычислении пределов для устранения неопределённостей видов
- 32. Правило Лопиталя
- 33. Задача Пример. Найти
- 34. Задача Пример. Найти Решение:
- 35. Задача Пример. Найти
- 36. Задача Пример. Найти Решение:
- 37. Задача Пример. Найти
- 38. Задача Пример. Найти Решение:
- 39. Производная Достаточные признаки монотонности
- 40. Производная 3. Если во всех точках
- 41. Точка является точкой
- 42. Точка является точкой
- 43. Экстремум Необходимое условие существования экстремума
- 44. Экстремум Достаточные условия существования экстремума
- 45. Экстремум Если функция дважды дифференцируема в некоторой
- 46. Экстремум Для отыскания наибольшего и
- 47. Задача Пример. Найти наибольшее и наименьшее значения
- 48. Задача Пример. Найти наибольшее и наименьшее значения
- 49. Функция называется выпуклой вниз (или
- 50. Функция называется выпуклой вверх (или
- 51. Производная Теорема. Функция вогнута на
- 52. Производная Теорема (достаточное условие перегиба
- 53. Финансовый университет при Правительстве Российской Федерации Рекламная пауза
Слайд 1Финансовый университет
при Правительстве Российской Федерации
Тема №4.
Дифференциальное исчисление
Слайд 2Производной функции в точке называется предел, если он существует и конечен,
отношения приращения функции к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю.
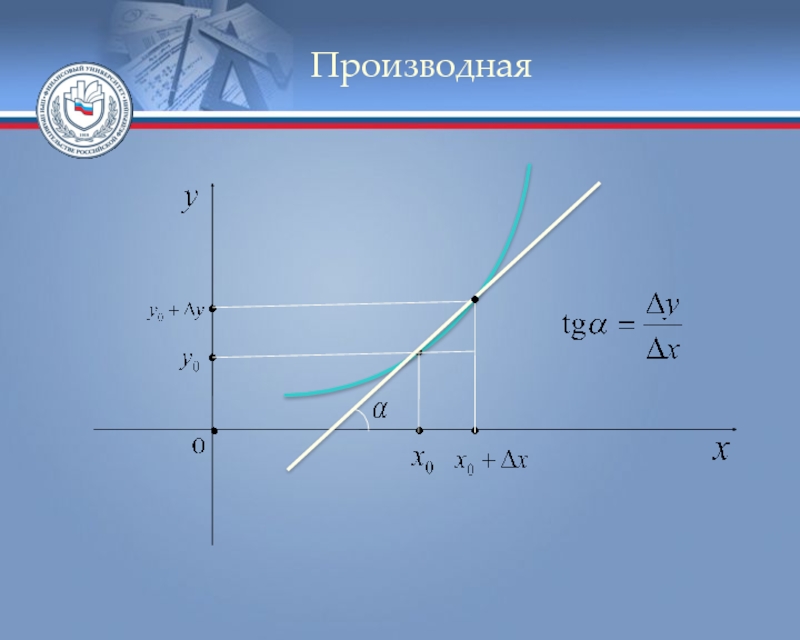
Слайд 4Производная
Геометрический смысл производной функции: производная функции в точке равна
тангенсу угла наклона касательной, проведённой к графику функции в этой точке с положительным направлением оси 0х.
Уравнение касательной к графику функции, проведённой в точке с учётом геометрического смысла производной имеет вид:
Уравнение касательной к графику функции, проведённой в точке с учётом геометрического смысла производной имеет вид:
Слайд 5Производная
Нахождение производной функции называется дифференцированием функции.
Критерий дифференцируемости функции в точке: Чтобы функция была дифференцируемой в некоторой точке необходимо и достаточно, чтобы она в этой точке имела конечную производную.
Функция называется дифференцируемой на множестве, если она дифференцируема в каждой точке этого множества.
Функция называется дифференцируемой на множестве, если она дифференцируема в каждой точке этого множества.
Слайд 6 Теорема (Необходимое условие дифференцируемости функции): Если функция дифференцируема в
некоторой точке, то она в этой точке непрерывна. (Обратное утверждение неверно).
Слайд 10Производная
Производная сложной функции
При условии, что функции имеют производные в
соответствующих точках.
Слайд 17Задача
Написать уравнение касательной к графику
функции
в точке его пересечения с
осью ординат.
осью ординат.
Слайд 20 Эластичностью функции называется предел отношения относительного приращения функции к
относительному приращению переменной, когда приращение этой переменной стремится к нулю.
Слайд 22Эластичность
Эластичность функции приближённо показывает на сколько процентов изменится функция
при изменении независимой переменной на 1%.
Слайд 23Свойства эластичности
Эластичность функции равна произведению независимой переменной на темп изменения функции
Слайд 25Задача
Пример. Зависимость между себестоимостью единицы продукции y (тыс.руб.) и выпуском продукции
х (млн.руб.) выражается функцией
Найти эластичность себестоимости при выпуске продукции, равном 150 млн.руб.
Найти эластичность себестоимости при выпуске продукции, равном 150 млн.руб.
Слайд 26Задача
Решение:
Получили то, что при выпуске продукции, равном 150 млн.руб. увеличение этого
выпуска на 1% приведёт к снижению себестоимости на 3%.
Слайд 27Производная
Основные теоремы дифференциального исчисления:
1. Теорема Ферма. Если дифференцируемая на
множестве функция достигает наибольшего или наименьшего значения в какой-либо точке этого множества, то производная функции в этой точке равна нулю.
Слайд 28Производная
2. Теорема Ролля. Пусть функция непрерывна на некотором отрезке, дифференцируема внутри
отрезка и на концах отрезка принимает равные значения, то внутри отрезка найдётся хотя бы одна точка, в которой производная функции равна нулю.
Слайд 29Производная
3. Теорема Лагранжа. Пусть функция непрерывна на некотором отрезке [a; b],
дифференцируема внутри отрезка (на интервале (a; b) ), то на этом интервале найдётся хотя бы одна точка , для которой справедливо равенство:
Слайд 30Производная
4. Теорема Ферма. Пусть функции непрерывны на некотором отрезке [a; b],
дифференцируемы на интервале (a; b) и во вех точках этого интервала, то на этом интервале найдётся хотя бы одна точка , для которой справедливо равенство:
Слайд 39Производная
Достаточные признаки монотонности функции:
Если во
всех точках некоторого множества производная дифференцируемой функции положительна, то функция на этом множестве возрастает;
Если во всех точках некоторого множества производная дифференцируемой функции отрицательна, то функция на этом множестве убывает;
Если во всех точках некоторого множества производная дифференцируемой функции отрицательна, то функция на этом множестве убывает;
Слайд 40Производная
3. Если во всех точках некоторого множества производная дифференцируемой функции
равна нулю, то функция на этом множестве постоянна;
Слайд 41 Точка является точкой максимума функции
, если найдётся такая окрестность этой точки, во всех точках которой выполнено неравенство:
Слайд 42 Точка является точкой минимума функции
, если найдётся такая окрестность этой точки, во всех точках которой выполнено неравенство:
Точки максимума и минимума являются точками экстремума (локального экстремума) функции.
Точки максимума и минимума являются точками экстремума (локального экстремума) функции.
Слайд 43Экстремум
Необходимое условие существования экстремума функции в точке: Если в
некоторой точке дифференцируемая функция достигает экстремума, то её производная в этой точке или равна нулю, или не существует.
Точки в которых производная функции или равна нулю, или не существует называются критическими (стационарными).
Точки в которых производная функции или равна нулю, или не существует называются критическими (стационарными).
Слайд 44Экстремум
Достаточные условия существования экстремума функции в точке:
1. Если найдётся
такая окрестность критической точки, во всех точках которой функция дифференцируема и её производная справа от критической точки знакопостоянна и отличается знаком от производной функции слева, то в этой критической точке функция достигает экстремума, причём, если производная слева положительна, а справа отрицательна, то максимума, а если наоборот, то минимума.
Слайд 45Экстремум
Если функция дважды дифференцируема в некоторой точке и в этой точке
производная первого порядка равна нулю, а производная второго порядка отлична от нуля, то функция в этой точке достигает экстремума, причём максимума, если вторая производная отрицательна и минимума – если положительна.
(Количество дифференцирований определяет порядок производной).
(Количество дифференцирований определяет порядок производной).
Слайд 46Экстремум
Для отыскания наибольшего и наименьшего значений функции
на отрезке следует:
Найти производную функции
Найти критические точки функции из уравнения
Найти значения функции в критических точках, принадлежащих данному отрезку и на концах этого отрезка;
Среди этих значений выбрать наибольшее и наименьшее значения.
Найти производную функции
Найти критические точки функции из уравнения
Найти значения функции в критических точках, принадлежащих данному отрезку и на концах этого отрезка;
Среди этих значений выбрать наибольшее и наименьшее значения.
Слайд 49 Функция называется выпуклой вниз (или вогнутой) на множестве, если
для любых двух значений из ООФ выполняется неравенство
Слайд 50 Функция называется выпуклой вверх (или выпуклой) на множестве, если
для любых двух значений из ООФ выполняется неравенство
Слайд 51Производная
Теорема. Функция вогнута на множестве тогда и только тогда,
когда её первая производная на этом множестве возрастает (вторая производная положительна).
Теорема. Функция выпукла на множестве тогда и только тогда, когда её первая производная на этом множестве убывает (вторая производная отрицательна).
Теорема. Функция выпукла на множестве тогда и только тогда, когда её первая производная на этом множестве убывает (вторая производная отрицательна).
Слайд 52Производная
Теорема (достаточное условие перегиба функции). Если вторая производная дважды
дифференцируемой функции при переходе через некоторую точку меняет свой знак, то эта точка является точкой перегиба её графика.
