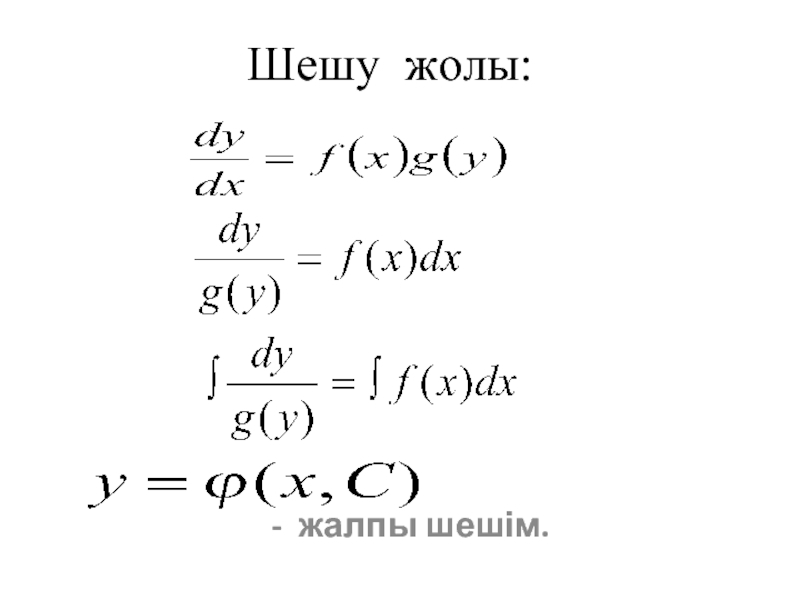- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дифференциалдық теңдеулер презентация
Содержание
- 1. Дифференциалдық теңдеулер
- 2. Дәріс жоспары: Бірінші ретті қарапайым дифференциалдық теңдеулер.
- 3. Дифференциалдық теңдеу деп x тәуелсіз
- 4. n-ші ретті дифференциалдық теңдеулер : F(x,y,y′,y′′,...,у(n))=0 n-
- 5. Дифференциалдық теңдеудің шешімі деп сол
- 6. n-ші ретті д.т. жалпы және дербес
- 7. 1-ші ретті қарапайым дифференциалдық теңдеу: F(x,y,y′)=0
- 8. Айнымалылары ажыратылатын дифференциалдық теңдеулер немесе
- 9. Шешу жолы:
- 10. Коши есебі
- 11. Бірінші ретті біртекті дифференциалдық теңдеу Анықтама. Егер
- 12. Бірінші ретті біртекті дифференциалдық теңдеу
- 13. Бірінші ретті сызықты дифференциалдық теңдеу у' +
- 14. Сызықты біртекті д.т. шешу әдісі у'+р(х) у
- 15. Біртекті сызықты емес д.т. шешу әдістері
- 16. Тұрақтыны вариациялау әдісі 1. С.б.емес д.т. жалпы
- 17. Тұрақтыны вариациялау әдісі Бұл әдіс үш этаптан
- 18. Тұрақтыны вариациялау әдісі В) теңдеудің дербес шешімін
- 19. С)
- 20. Бернулли әдісі С.б. емес д.т. шешімі
- 21. Бернулли теңдеуі
- 22. Кейбір жаратылыстану есептеріне д.т. құру:
- 23. Бактериялардың көбею жылдамдығы жөніндегі есеп Бактериялардың
- 24. Химиялық реакцияларды сипаттайтын д.т.:
- 25. Радиоактивті ыдырау жөніндегі есеп Радийдің ыдырау жылдамдығы
- 26. Дененің тоңазуы жөніндегі есеп Дененің ауада
- 27. Әдебиет: ҚАЗАҚ ТІЛІНДЕ Изтлеуов М.К.,
- 28. Назарларыңызға рахмет
Слайд 1Дифференциалдық
теңдеулер
Медициналық биофизика, информатика және математикалық статистика кафедрасының доценті
Аймаханова Айзат Шалхаровна
Слайд 2Дәріс жоспары:
Бірінші ретті қарапайым дифференциалдық теңдеулер. Жалпы және дербес шешімдер.
Айнымалылары ажыратылатын
Бір текті дифференциалдық теңдеу.
Бірінші ретті сызықтық дифференциалдық теңдеулер. Лагранж әдісі. Бернулли әдісі.
Медициналық – биологиялық есептерге дифференциалдық теңдеулер құру.
Слайд 3
Дифференциалдық теңдеу деп x тәуелсіз айнымалыны, y ізделінді функцияны және
Дифференциалдық теңдеудің құрамына кіретін туындылардың ең жоғары реті сол теңдеудің реті деп аталады.
Егер y ізделінді функциясы бір айнымалыға тәуелді болса, онда д.т. қарапайым дифференциалдық теңдеу деп аталады.
Слайд 4n-ші ретті дифференциалдық теңдеулер :
F(x,y,y′,y′′,...,у(n))=0
n- дифференциалдық теңдеудің реті
Жоғары туындыға қатысты шешілген
Слайд 5
Дифференциалдық теңдеудің шешімі деп сол теңдеуге қойғанда оны теңбе-теңдікке айналдыратын
Дифференциалдық теңдеудің шешімін табу есебі берілген дифференциалдық теңдеуді интегралдау есебі деп аталады.
Дифференциалдық теңдеудің шешімінің графигі интегралдық қисық деп аталады.
Слайд 6 n-ші ретті д.т. жалпы және дербес шешімдері
y=ϕ(x,C1,..,Cn), - жалпы
мұндағы C1,..,Cn кез келген тұрақты сандар.
C1,..,Cn нақты бір сандық мәндеріндегі шешім дербес шешім деп аталады.
Слайд 7 1-ші ретті қарапайым дифференциалдық теңдеу:
F(x,y,y′)=0
х – тәуелсіз айнымалы; у -
y′=f (x,y)
туындыға қатысты шешілетін бірінші ретті д.т.
Слайд 8Айнымалылары ажыратылатын дифференциалдық теңдеулер
немесе
мұндағы f (x), M(x),P(x) – х айнымалысының қандай
g(y), N(y), Q(y) - у айнымалысының функциясы.
Слайд 10 Коши есебі
бастапқы шартын қанағаттандыратын у' = f (x,у) теңдеуінің дербес шешімін табу есебі Коши есебі деп аталады.
Слайд 11Бірінші ретті біртекті дифференциалдық теңдеу
Анықтама. Егер х және у айнымалылары бойынша
функция болатын болса, онда бірінші ретті дифференциалдық теңдеу
біртекті теңдеу деп аталады.
Біртекті теңдеудің шешуі. Шарт бойынша
Онда теңдеу төмендегі түрге ие болады:
Слайд 12Бірінші ретті біртекті дифференциалдық теңдеу
Соңғы теңдікті дифференциалдап, табатынымыз:
және -тің мәндерін берілген теңдеуге қойып,
теңдеуіне ие боламыз. Бұл айнымалылары бөлінетін теңдеу:
немесе
Интегралдап табамыз:
немесе
Слайд 13Бірінші ретті сызықты дифференциалдық теңдеу
у' + р(х) у = f (х),
мұндағы р(х) и f(х) — үздіксіз функциялар,
Егер f (х) = 0, онда у'+р(х)у=0
біртекті сызықты д.т.
Егер f (х)≠0, онда у'+р(х)у=f (х),
біртекті сызықты емес д.т.
Слайд 15Біртекті сызықты емес д.т. шешу әдістері
Тұрақтыны вариациялау әдісі
( Лагранж әдісі)
Бернулли әдісі
Слайд 16Тұрақтыны вариациялау әдісі
1. С.б.емес д.т. жалпы шешімін адымдап табу әдісі.
2. Жалпы
Слайд 17Тұрақтыны вариациялау әдісі
Бұл әдіс үш этаптан тұрады.
А)
сызықтық біртекті теңдеудің жалпы
Слайд 18Тұрақтыны вариациялау әдісі
В) теңдеудің дербес шешімін табу үшін С х
Слайд 19
С) функциясының табылған мәнін
қойып, табамыз:
(*)
(*) - бірінші ретті сызықтық бір текті емес теңдеудің жалпы шешімі.
Слайд 20 Бернулли әдісі
С.б. емес д.т. шешімі мына түрде ізделінеді
мұндағы
Слайд 21Бернулли теңдеуі
Егер немесе болатын болса, онда сызықтық дифференциалдық
теңдеуге ие боламыз. Сондықтан және жағдайда қарастырамыз.
Бұл теңдеу Бернулли теңдеуі деп аталады және алмастыруы
арқылы сызықтық дифференциалдық теңдеуге келтіріледі. Ол үшін теңдеудің екі
жағын да бөліп: (1) теңдеуін аламыз.
(2) алмастыруын жасаймыз.
(2) теңдікті дифференциалдап, табамыз:
(3)
z және -тің мәндерін (1) теңдеуге қойып, төмендегі сызықтық
дифференциалдық теңдеуге ие боламыз:
(4)
Бұл теңдеудің жалпы интегралын тауып және z-ті арқылы алмастырып,
Бернулли теңдеуінің жалпы интегралын табамыз.
Слайд 23Бактериялардың көбею жылдамдығы жөніндегі есеп
Бактериялардың көбею жылдамдығы олардың санына пропорционал. Бастапқы
Слайд 25Радиоактивті ыдырау жөніндегі есеп
Радийдің ыдырау жылдамдығы уақыттың әрбір мезетінде оның бар
Слайд 26Дененің тоңазуы жөніндегі есеп
Дененің ауада тоңазу жылдамдығы дене температурасы мен ауа
Слайд 27Әдебиет:
ҚАЗАҚ ТІЛІНДЕ
Изтлеуов М.К., Беккужина А.И., Жалимбетова Н.К., Ахметова А.Б. Математика: Жоғары
Қасымов К., Қасымов Е. Жоғары математика курсы. Оқу қуралы.-Алматы: Санат, 1997.
ОРЫС ТІЛІНДЕ
И.В. Павлушков и др. Основы высшей математики и математической статистики. (учебник для медицинских и фармацевтических вузов)., М., 2003 г.
В.С. Шипачев. Курс высшей математики. М., Проспект. 2004 г.
И.И. Баврин, В.Л. Матросов. Высшая математика. М., ВЛАДОС.2002г.
Ю. Морозов. Основы высшей математики для мед. вузов. М., 2000 г.