- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
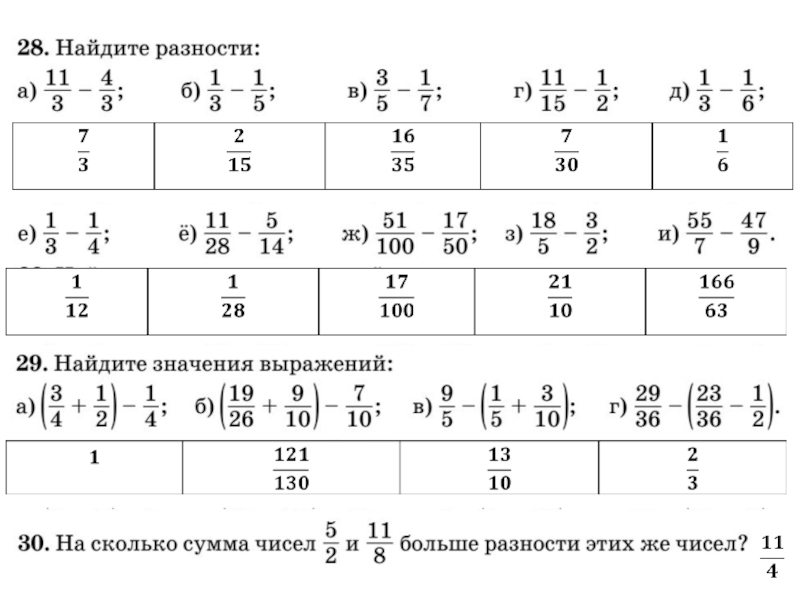
Действия с дробями презентация
Содержание
- 1. Действия с дробями
- 2.
- 3. Стр. 241 1. ПРОБА
- 4. Сложение и вычитание смешанных дробей Сумма смешанных
- 5. Сложение и вычитание смешанных дробей Сумма смешанных
- 6. Сложение и вычитание смешанных дробей Сумма
- 7. Сложение и вычитание смешанных дробей Правило поиска
- 8. 18 13 18 5 5+ Сложение и
- 9. Сложение и вычитание смешанных дробей Особенности поиска
- 10. Сложение и вычитание смешанных дробей Вычитание смешанных
- 11. Сложение и вычитание смешанных дробей Вычитание смешанных
- 12. Сложение и вычитание смешанных дробей Вычитание смешанных
- 13. Сложение и вычитание смешанных дробей Вычитание смешанных
- 14. Сложение и вычитание смешанных дробей Вычитание смешанных
- 15. Сложение и вычитание смешанных дробей Вычитание смешанных
- 16. Сложение и вычитание смешанных дробей Вычитание смешанных
- 17. №3 2. Закрепление №1 №2
- 18. Какие существуют способы вычисления суммы (разности) смешанных
- 19. Домашнее задание стр. 242 №7, стр.
Слайд 4Сложение и вычитание
смешанных дробей
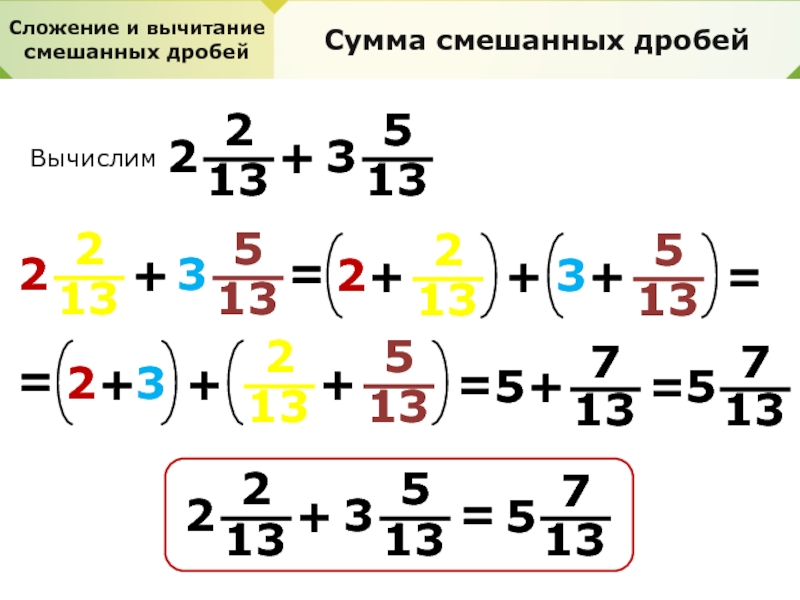
Сумма смешанных дробей
Сумму смешанных дробей можно найти, записав
При этом мы будем действовать так же,
как при сложении правильных дробей.
Однако в этом случае вычисления
могут быть громоздкими, трудоёмкими.
Поэтому для удобства вычислений обычно используют другой способ, основанный на
свойствах действия сложения.
Слайд 5Сложение и вычитание
смешанных дробей
Сумма смешанных дробей
Для дробей справедливы переместительное и сочетательное
a
m
n
+
k
b
=
k
b
+
m
n
m
n
+
=
k
b
+
a
z
m
n
+
k
b
+
z
Слайд 6
Сложение и вычитание
смешанных дробей
Сумма смешанных дробей
Вычислим
2
13
2
+
5
13
3
2
13
2
+
5
13
3
=
2
13
2
+
+
5
13
3
+
=
=
2
+
+
5
13
3
+
=
2
13
+
5
=
13
7
5
13
7
2
13
2
+
5
13
3
=
5
13
7
Слайд 7Сложение и вычитание
смешанных дробей
Правило поиска суммы смешанных дробей
Чтобы сложить смешанные дроби,
можно
и отдельно дробные части.
По этому же правилу складываем
натуральные числа и смешанные дроби,
считая, что натуральное число
имеет дробную часть, равную нулю.
2
+
5
13
3
=
5
13
5
Слайд 818
13
18
5
5+
Сложение и вычитание
смешанных дробей
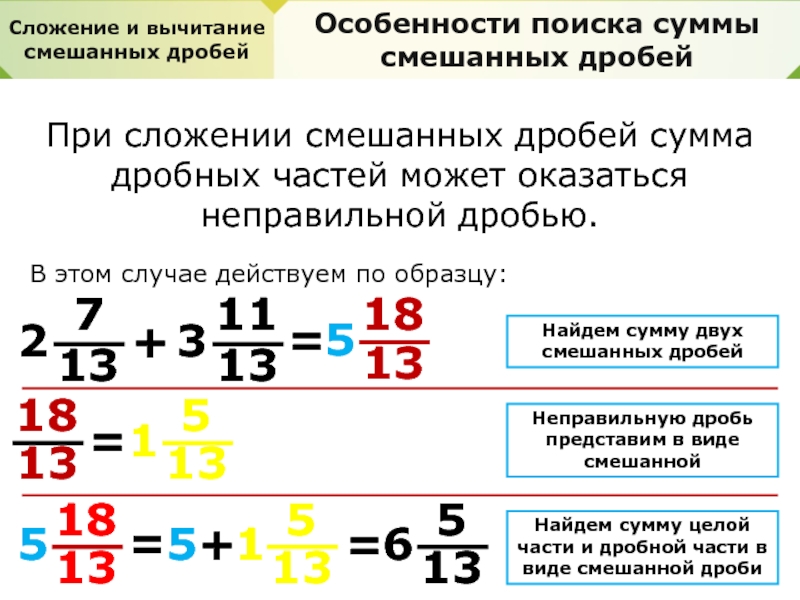
Особенности поиска суммы смешанных дробей
При сложении смешанных дробей
В этом случае действуем по образцу:
7
13
2
+
11
13
3
=
5
13
13
18
=
13
1
5
=
13
5
1
=
6
13
5
Найдем сумму двух смешанных дробей
Неправильную дробь представим в виде смешанной
Найдем сумму целой части и дробной части в виде смешанной дроби
Слайд 9Сложение и вычитание
смешанных дробей
Особенности поиска суммы смешанных дробей
Если дробные части смешанных
то при сложении их нужно привести сначала к общему знаменателю.
3
8
2
+
5
12
3
=
3
8
2
+
5
12
3
/3
/2
=
=
9
24
2
+
10
24
3
=
19
24
5
Слайд 10Сложение и вычитание
смешанных дробей
Вычитание смешанных дробей
Целая часть уменьшаемого больше,
чем целая
и дробная часть уменьшаемого больше, чем дробная часть вычитаемого.
5
17
3
–
2
17
2
=
3
–
+
2
17
2
–
5
17
=
1
+
3
17
=
1
3
17
=
Слайд 11Сложение и вычитание
смешанных дробей
Вычитание смешанных дробей
Дробные части
уменьшаемого и вычитаемого равны
5
12
3
–
5
12
2
=
3
–
+
5
12
2
–
5
12
=
1
+
0
12
=
1
=
Слайд 12Сложение и вычитание
смешанных дробей
Вычитание смешанных дробей
Целые части
уменьшаемого и вычитаемого равны
5
17
3
–
2
17
3
=
3
–
+
2
17
3
–
5
17
=
0
+
3
17
=
=
3
17
Слайд 13Сложение и вычитание
смешанных дробей
Вычитание смешанных дробей
Целая часть уменьшаемого больше,
чем целая часть
а дробная часть уменьшаемого меньше, чем дробная часть вычитаемого.
5
12
4
–
7
12
2
=
В этом случае в целой части уменьшаемого «занимают» единицу.
3
+
5
12
1
–
7
12
2
=
=
3
+
17
12
–
7
12
2
=
–
1
+
10
12
=
1
5
6
Слайд 14Сложение и вычитание
смешанных дробей
Вычитание смешанных дробей
Уменьшаемое – смешанная дробь, вычитаемое –
5
12
4
–
2
=
4
–
+
0
2
–
5
12
=
2
+
5
12
=
=
5
12
2
Слайд 15Сложение и вычитание
смешанных дробей
Вычитание смешанных дробей
Уменьшаемое – натуральное число, вычитаемое –
4
–
7
12
2
=
3
+
12
12
–
7
12
2
=
=
3
+
12
12
–
7
12
2
=
–
1
+
5
12
=
1
5
12
Слайд 16Сложение и вычитание
смешанных дробей
Вычитание смешанных дробей
Дробные части уменьшаемого и вычитаемого имеют
В этом случае приводим сначала дробные части к общему знаменателю.
11
12
3
–
5
6
2
=
/2
11
12
3
–
10
12
2
=
1
12
1
Слайд 18Какие существуют способы вычисления суммы (разности) смешанных дробей?
ПРОВЕРЬ СЕБЯ
Ответьте на следующие
Сложение и вычитание
смешанных дробей
Как вычислить сумму (разность) смешанных дробей с разными знаменателями?
Вычислите сумму и разность смешанных дробей:
и ; и ; и .
5
7
3
5
8
2
2
3
3
1
3
3
1
9
5
1
9
4