- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Делимость натуральных чисел презентация
Содержание
- 1. Делимость натуральных чисел
- 2. Замечание: Вопрос о существовании разности на множестве
- 3. Для операции деления такого простого признака
- 4. Определение отношения делимости натуральных чисел Пусть даны
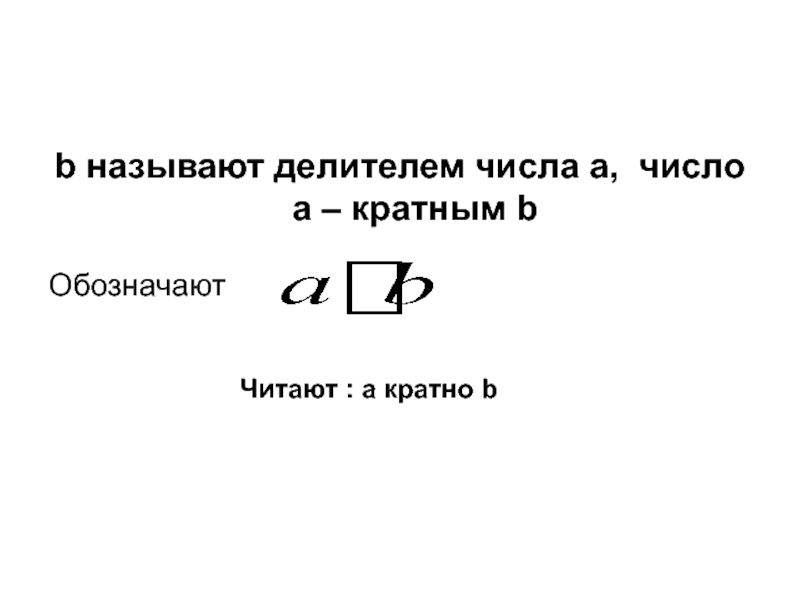
- 5. b называют делителем числа a, число a
- 6. Что общего и что различного в
- 7. 24 : 5 - число 5
- 8. Уточним понятие «отношение делимости» 1. Единица
- 9. Доказательство: Так как ,
- 10. Следствие: Множество делителей данного числа конечно. Например: Делители числа 36 образуют конечное множество
- 11. Сопутствующие понятия Простые и составные числа Определение:
- 12. Например: Число 7 – простое. Число 2
- 13. Определение: Составным числом называется натуральное число,
- 14. Чисел кратных данному числу, бесконечное множество. Например: Числа кратные 6 образуют множество:
- 15. Общий вид чисел, кратных 6: x=6·n,
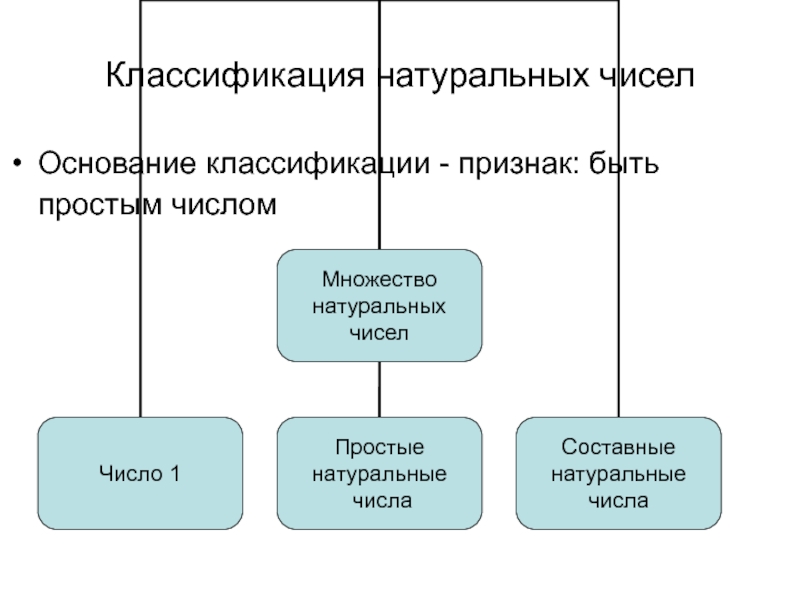
- 16. Классификация натуральных чисел Основание классификации - признак: быть простым числом
- 17. Свойства отношения делимости 1. Отношение делимости рефлексивно,
- 18. Теорема 1. Отношение делимости рефлексивно. (любое натуральное
- 19. Доказательство Для любого натурального a справедливо
- 20. Теорема 2 Отношение делимости антисиммет-рично (если a
- 21. Доказательство: (доказательство осуществляется методом от противного) Предположим
- 22. Теорема 3 Отношение делимости транзитивно. Если отношение
- 23. Доказательство Если , то
- 24. Признак делимости суммы Теорема 4 Если каждое
- 25. Доказательство Если то
- 26. Преобразуем сумму чисел Так
- 27. Замечание Обратная теорема: если сумма натуральных чисел
- 28. Признак делимости разности Теорема 5 Если уменьшаемое
- 29. Обобщение теоремы 5 Теорема:
- 30. Краткое условие теоремы Дано: a>b и Доказать, что
- 31. Доказательство Рассмотрим разность чисел a и b. Следовательно, (a-b) кратно с
- 32. Например: Задание: Не выполняя вычислений, определите делится
- 33. Признак делимости произведения Теорема 6 Если число
- 34. Доказательство Так как
- 35. Следствие: Если один из множителей произведения делится
- 36. Еще три теоремы о делимости Теорема
- 37. Доказательство Пусть И известно, что Доказательство проведем методом «от противного»
- 38. Предположим противное. Пусть Преобразуем сумму
- 39. Теорема 2. (задача) Если в произведении a·b
- 40. Теорема 3. Если произведение a·c делится на
- 41. Доказательство Так как Значит ассоциативный
- 42. Спасибо за внимание!
Замечание: Вопрос о существовании разности на множестве натуральных чисел решается очень просто: достаточно, чтобы уменьшаемое было больше вычитаемого. a-b существует, если a>b, где
Слайд 2Замечание:
Вопрос о существовании разности на множестве натуральных чисел решается очень просто:
достаточно, чтобы уменьшаемое было больше вычитаемого.
a-b существует, если a>b,
где
a-b существует, если a>b,
где
Слайд 3Для операции деления такого
простого признака нет.
Поэтому и возникла в математике
теория делимости натуральных чисел.
Слайд 4Определение отношения делимости натуральных чисел
Пусть даны натуральные числа a и b.
Говорят,
что число a делится на b, если существует такое натуральное
что
что
Слайд 7 24 : 5 - число 5 есть делитель. Компонент действия
деления.
24 : 6 число 6 – не только делитель (компонент действия деления), но и делитель числа 24, так как 24=6·4.
Число b называется делителем числа a тогда, когда число a есть кратное b.
24 : 6 число 6 – не только делитель (компонент действия деления), но и делитель числа 24, так как 24=6·4.
Число b называется делителем числа a тогда, когда число a есть кратное b.
Слайд 8Уточним понятие
«отношение делимости»
1. Единица (число 1) является делителем любого натурального
числа, так как a=1·a.
2. Теорема №1.
Делитель b данного числа a не превышает этого числа.
Если
2. Теорема №1.
Делитель b данного числа a не превышает этого числа.
Если
Слайд 9Доказательство:
Так как
, то существует такое
, что a = b·g
Значит,
a - b =b·g – b = b ·(g -1)
Так как
, то g ≥ 1
Тогда, b·(g-1) ≥ 0
Следовательно, b ≤ a
Слайд 10Следствие:
Множество делителей данного числа конечно.
Например:
Делители числа 36 образуют конечное множество
Слайд 11Сопутствующие понятия
Простые и составные числа
Определение:
Простым числом называется такое натуральное число, большее
1, которое имеет только два делителя – единицу и само это число.
Слайд 12Например:
Число 7 – простое.
Число 2 – простое.
(единственное простое четное число).
Числа
3,11,19, 23, 117 ... являются простыми, так как эти числа имеют по два делителя.
Число 1 ……?
Число 1 ……?
Слайд 13Определение:
Составным числом называется натуральное число, которое имеет более двух делителей.
Например:
4,6,12,121, 45, 225 – составные числа.
Число 1- составное?
Число 1- составное?
Слайд 14Чисел кратных данному числу, бесконечное множество.
Например:
Числа кратные 6 образуют множество:
Слайд 15
Общий вид чисел, кратных 6:
x=6·n,
Общий вид чисел, кратных 5:
x=5·n,
Общий вид чисел, кратных k:
x=k·n,
Общий вид чисел, кратных k:
x=k·n,
Слайд 17Свойства отношения делимости
1. Отношение делимости рефлексивно, антисимметрично и транзитивно.
2. Отношение делимости
есть отношение нестрогого порядка
Слайд 18Теорема 1.
Отношение делимости рефлексивно.
(любое натуральное число делится само на себя).
Если отношение
делимости
обозначить –R, а элемент –n, то свойство рефлекcивности имеет вид: n R n
обозначить –R, а элемент –n, то свойство рефлекcивности имеет вид: n R n
Слайд 19Доказательство
Для любого натурального a
справедливо равенство a=a·1.
по определению делимости
Что и требовалось
доказать.
Слайд 20Теорема 2
Отношение делимости антисиммет-рично (если a кратно b, то b не
кратно a)
Если отношение делимости
обозначить –R, а элементы отношения – a и b, то свойство антисимметричности имеет вид:
если a R b, то b R a
Если отношение делимости
обозначить –R, а элементы отношения – a и b, то свойство антисимметричности имеет вид:
если a R b, то b R a
Слайд 21Доказательство:
(доказательство осуществляется методом от противного)
Предположим обратное.
Пусть
но тогда a ≤
b.
По условию
Следовательно, a ≥ b
Неравенства a ≤ b и a ≥ b справедливы, если a=b. Противоречие.
Значит наше предположение не верно.
Слайд 22Теорема 3
Отношение делимости транзитивно.
Если отношение делимости
обозначить –R, а элементы отношения
– a,b,c то свойство транзитивности имеет вид:
если a R b и b R c, то a R c .
если a R b и b R c, то a R c .
Если
и
, то
Слайд 23Доказательство
Если
, то
такое, что
a = b · g
Если
, то
такое, что
Тогда
имеем: a = b·g = (c·p)·g = c·(p·g)
Число p · g – натуральное. Значит :
ассоциативный
Слайд 24Признак делимости суммы
Теорема 4
Если каждое из натуральных чисел
делится на натуральное число
b, то
делится на это число.
Слайд 25Доказательство
Если
то
Если
то
- - - - - - - -
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Если
то
Слайд 26Преобразуем сумму чисел
Так как сумма натуральных чисел есть натуральное число, то
ее можно заменить натуральным числом g. Следовательно,
А это значит, что сумма
делится на b.
дистрибутивный
Слайд 27Замечание
Обратная теорема: если сумма натуральных чисел кратна натуральному числу c, то
каждое слагаемое кратно этому числу c.
Обратная теорема не верна.
25=12+13
Теорема о делимости суммы есть необходимое условие, но не достаточное
Обратная теорема не верна.
25=12+13
Теорема о делимости суммы есть необходимое условие, но не достаточное
Слайд 28Признак делимости разности
Теорема 5
Если уменьшаемое a и вычитаемое b делятся на
число c, то и разность (a-b), где a>b, делится на c.
Доказать самостоятельно!
Слайд 29Обобщение теоремы 5
Теорема:
Разность двух натуральных чисел a и
b делится на натуральное число с, тогда и только тогда, когда a при делении на c и b при делении на c дают одинаковые остатки.
Слайд 32Например:
Задание: Не выполняя вычислений, определите делится ли разность чисел 247 и162
на 5.
247 при делении на 5 дает остаток 2 и
162 при делении на 5 дает остаток 2.
Значит разность 247-162 кратна 5.
Действительно 247-162=85,
85:5=17
247 при делении на 5 дает остаток 2 и
162 при делении на 5 дает остаток 2.
Значит разность 247-162 кратна 5.
Действительно 247-162=85,
85:5=17
Слайд 33Признак делимости произведения
Теорема 6
Если число a делится на b, то произведение
вида a·x, где x – натуральное число, делится на b.
Слайд 35Следствие:
Если один из множителей произведения делится на натуральное число, то и
все произведение делится на это натуральное число.
Например:
24·978:12=(24:12)·978=2·978=
=2·(900+70+8)=1800+140+16=1956
Например:
24·978:12=(24:12)·978=2·978=
=2·(900+70+8)=1800+140+16=1956
Слайд 36Еще три теоремы о делимости
Теорема 1
Если в сумме одно слагаемое
не делится на b, а все остальные слагаемые суммы делятся на b, то и вся сумма на b не делится.
Слайд 38Предположим противное.
Пусть
Преобразуем сумму s
Имеем:
Применим теорему о делимости разности.
Следовательно:
Противоречие
Значит наше предположение
не верно. Что и требовалось доказать.
Слайд 39Теорема 2. (задача)
Если в произведении a·b множитель a делится на натуральное
число m, а множитель b делится на натуральное число n, то произведение a·b делится на m·n.
Доказать самостоятельно!
Слайд 40Теорема 3.
Если произведение a·c делится на произведение b·c, причем c-натуральное число,
то a делится на b.
