- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
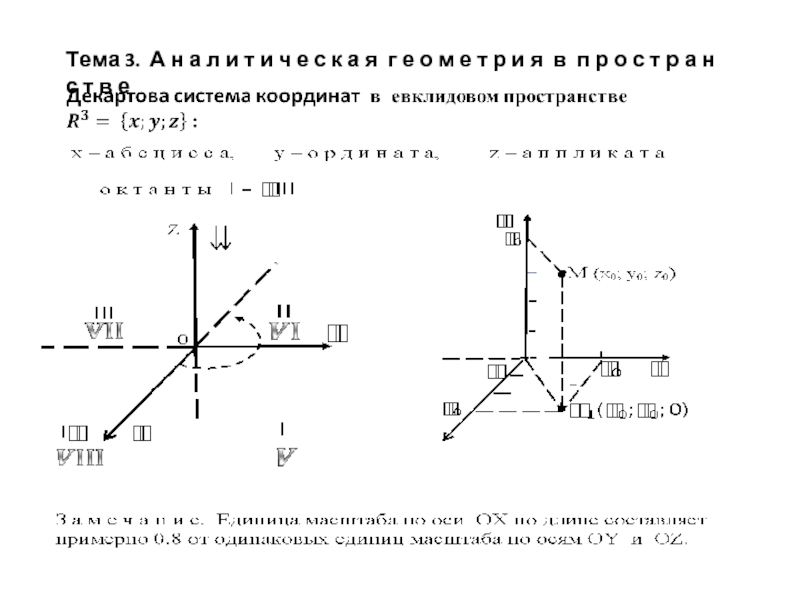
Декартова система координат в евклидовом пространстве презентация
Содержание
- 1. Декартова система координат в евклидовом пространстве
- 2. 1-51 Правило буравчика (правило правого винта)
- 4. РАЗДЕЛ 2. ПРЯМАЯ В ПРОСТРАНСТВЕ
- 5. РАЗДЕЛ 3. ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
- 6. Карл Фридрих Гаусс - родился 30
- 7.
- 8. Р е ш е н и е
- 9.
- 10.
- 11.
- 12. РАЗДЕЛ 4. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
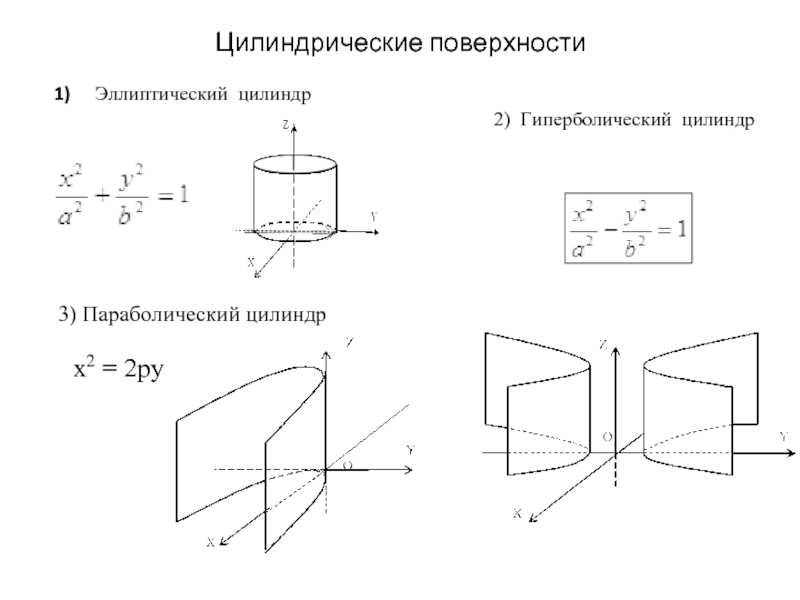
- 13. Цилиндрические поверхности Эллиптический цилиндр
- 14. Поверхности вращения
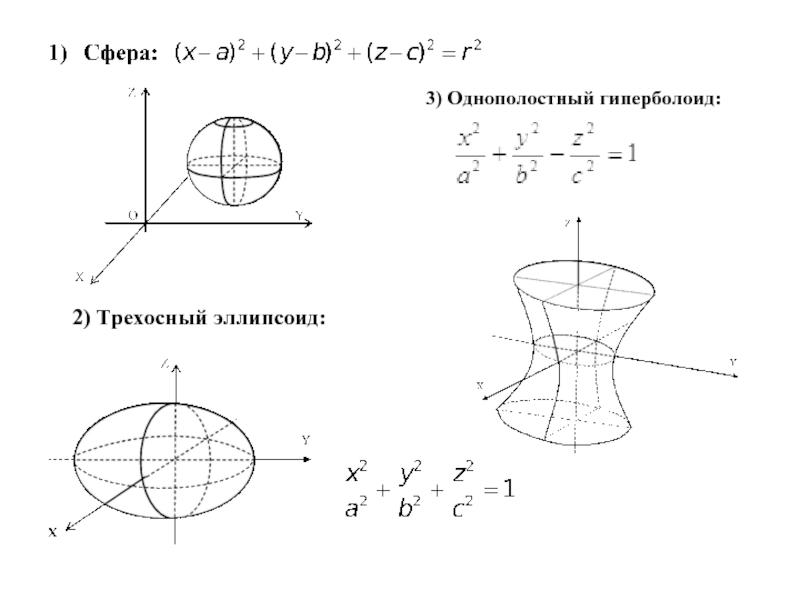
- 15. 3) Однополостный гиперболоид: 2) Трехосный эллипсоид:
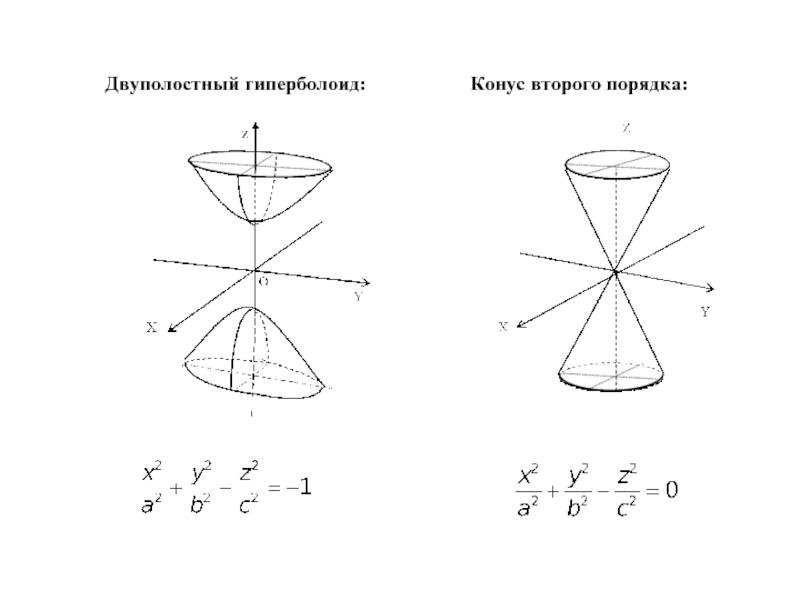
- 16. Двуполостный гиперболоид: Конус второго порядка:
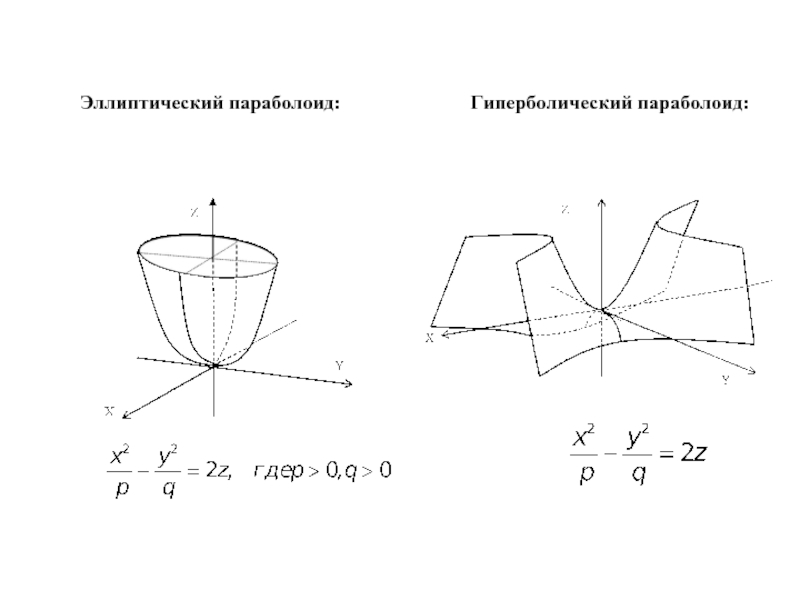
- 17. Эллиптический параболоид: Гиперболический параболоид:
Слайд 21-51
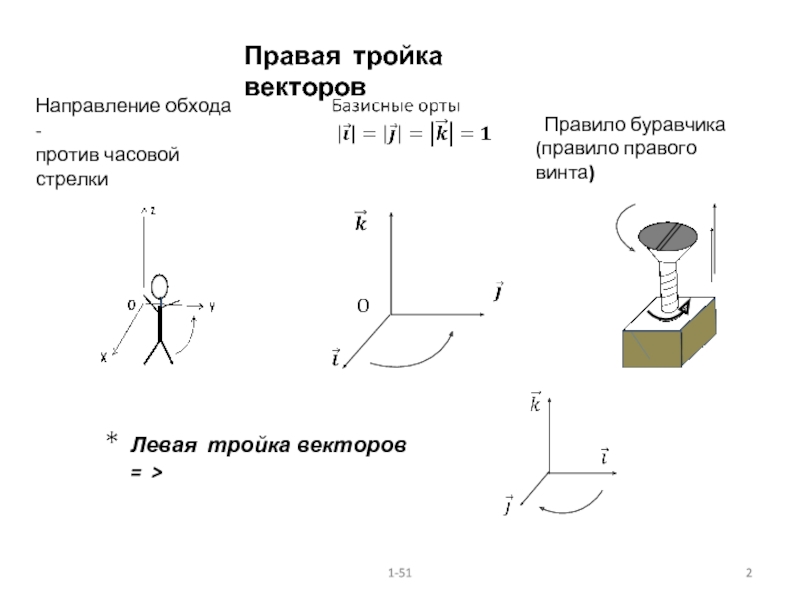
Правило буравчика
(правило правого винта)
Правая тройка векторов
Направление обхода -
против часовой
Левая тройка векторов = >
Слайд 4РАЗДЕЛ 2. ПРЯМАЯ В ПРОСТРАНСТВЕ
• Условия параллельности прямых
•
Слайд 6
Карл Фридрих Гаусс - родился 30 апреля 1777 года в Германии.
Считается "королем математики".
Занимался исследованиями в таких областях как:
алгебра, дифференциальная и неевклидовая геометрия, математический анализ, теории функций комплексного
переменного, теория вероятностей.
Слайд 12
РАЗДЕЛ 4. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Поверхности второго порядка – это поверхности, уравнения
• Цилиндрические поверхности.
Цилиндрическими поверхностями называются поверхности, образованные линиями, параллельными какой- либо фиксированной прямой.
Рассмотрим поверхности, в уравнении которых отсутствует составляющая z, т.е. направляющие параллельны оси Оz. Тип линии на плоскости ХOY (эта линия называется направляющей поверхности) определяет характер цилиндрической поверхности. Рассмотрим некоторые частные случаи в зависимости от уравнения направляющих: