- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Definition. Statistics презентация
Содержание
- 1. Definition. Statistics
- 2. Ex. 1a: Independent and Dependent Samples Classify
- 3. Ex. 1: Independent and Dependent Samples Sample
- 4. Ex. 1b: Independent and Dependent Samples Classify
- 5. Ex. 1b: Independent and Dependent Samples Sample
- 6. Note: Dependent samples often involve identical twins,
- 7. The t-Test for the Difference Between Means
- 8. To conduct the test, the following conditions
- 9. To conduct the test, the following conditions
- 10. The following symbols are used for the
- 11. Because the sampling distribution for
- 13. Ex. 2: The t-Test for the Difference
- 14. The claim is that “golfers can lower
- 15. Because the test is a right-tailed test,
- 16. Using the t-test, the standardized test statistic
- 17. Ex. 3: The t-Test for the Difference
- 18. If there is a change in the
- 19. Because the test is a tw0-tailed test,
- 20. Using the t-test, the standardized test statistic
- 21. Using Technology If you prefer to use
- 22. Using Technology Stat|Edit|enter data Subtract L1 –
Слайд 1Definition
Two samples are independent if the sample selected from one population
Слайд 2Ex. 1a: Independent and Dependent Samples
Classify each pair of samples as
Sample 1: Resting heart rates of 35 individuals before drinking coffee.
Sample 2: Resting heart rates of the same individuals after drinking two cups of coffee.
Слайд 3Ex. 1: Independent and Dependent Samples
Sample 1: Resting heart rates of
Sample 2: Resting heart rates of the same individuals after drinking two cups of coffee.
These samples are dependent. Because the resting heart rates of the same individuals were taken, the samples are related. The samples can be paired with respect to each individual.
Слайд 4Ex. 1b: Independent and Dependent Samples
Classify each pair of samples as
Sample 1: Test scores for 35 statistics students
Sample 2: Test scores for 42 biology students who do not study statistics
Слайд 5Ex. 1b: Independent and Dependent Samples
Sample 1: Test scores for 35
Sample 2: Test scores for 42 biology students who do not study statistics
These samples are independent. It is not possible to form a pairing between the members of samples—the sample sizes are different and the data represent test scores for different individuals.
Слайд 6Note:
Dependent samples often involve identical twins, before and after results for
Слайд 7The t-Test for the Difference Between Means
To perform a two-sample hypothesis
. The test statistic is the mean of these differences,
Слайд 8To conduct the test, the following conditions are required:
The samples must
Both populations must be normally distributed.
If these two requirements are met, then the sampling distribution for , the mean of the differences of the paired data entries in the dependent samples,
Слайд 9To conduct the test, the following conditions are required:
has a
Слайд 10The following symbols are used for the t-test for μd.
Although formulas
Слайд 11Because the sampling distribution for is a t-distribution, you
STUDY TIP: If n > 29, use the last row (∞) in the t-distribution table.
Слайд 13Ex. 2: The t-Test for the Difference Between Means
A golf club
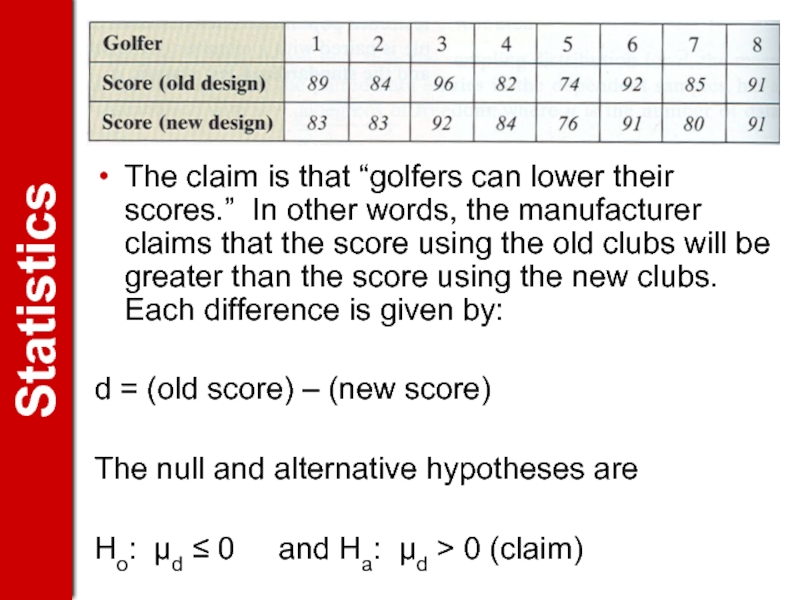
Слайд 14The claim is that “golfers can lower their scores.” In other
d = (old score) – (new score)
The null and alternative hypotheses are
Ho: μd ≤ 0 and Ha: μd > 0 (claim)
Слайд 15Because the test is a right-tailed test, α = 0.10, and
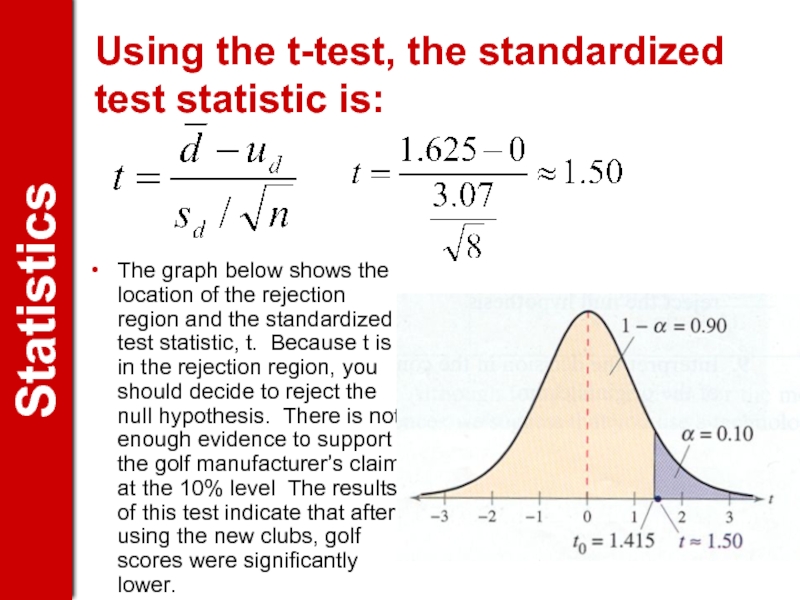
Слайд 16Using the t-test, the standardized test statistic is:
The graph below shows
Слайд 17Ex. 3: The t-Test for the Difference Between Means
A state legislator
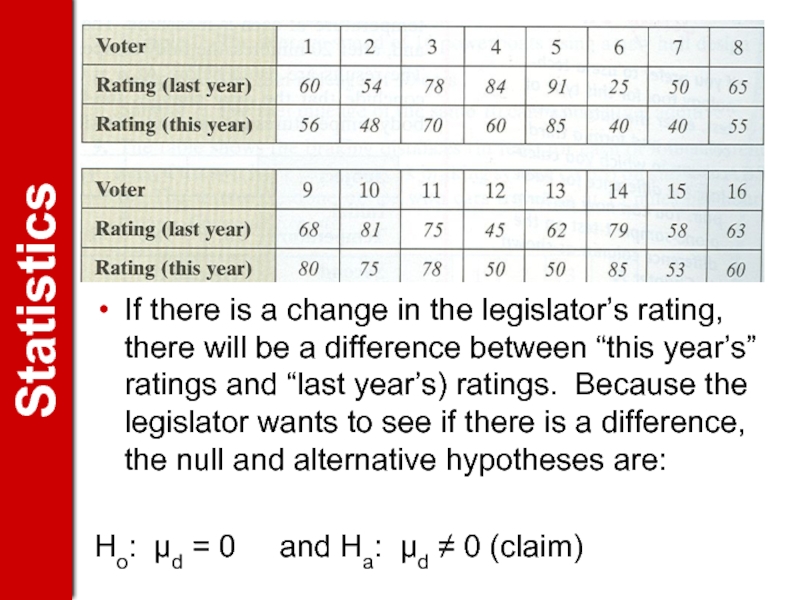
Слайд 18If there is a change in the legislator’s rating, there will
Ho: μd = 0 and Ha: μd ≠ 0 (claim)
Слайд 19Because the test is a tw0-tailed test, α = 0.01, and
Слайд 20Using the t-test, the standardized test statistic is:
The graph shows the
Слайд 21Using Technology
If you prefer to use a technology tool for this
Stat|Edit|enter data
Subtract L1 – L2 = in L3.
STAT|Tests|t-test
Data
μ = 0
List: L3
Freq: 1
μ ≠ 0
Calculate
Слайд 22Using Technology
Stat|Edit|enter data
Subtract L1 – L2 = in L3.
STAT|Tests|t-test
Data
μ = 0
List: L3
Freq: 1
μ ≠ 0
Calculate
μ ≠ 0
T = 1.369 (standardized test statistic)
P = don’t worry about it
X bar = 3.3125 – same as d bar.
Sx = 9.68 which is Sd
I find it easy to draw and enter the data into the curve part so I can visually see the rejection region. You will need to answer “reject” or “fail to reject” and answer whether or not there is enough evidence at whatever level given.