- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Числовые множества презентация
Содержание
- 1. Числовые множества
- 2. Множество Многое, мыслимое нами как единое целое
- 3. Георг Кантор Немецкий математик Создатель теории
- 4. Пример Множество студентов группы Множество людей в
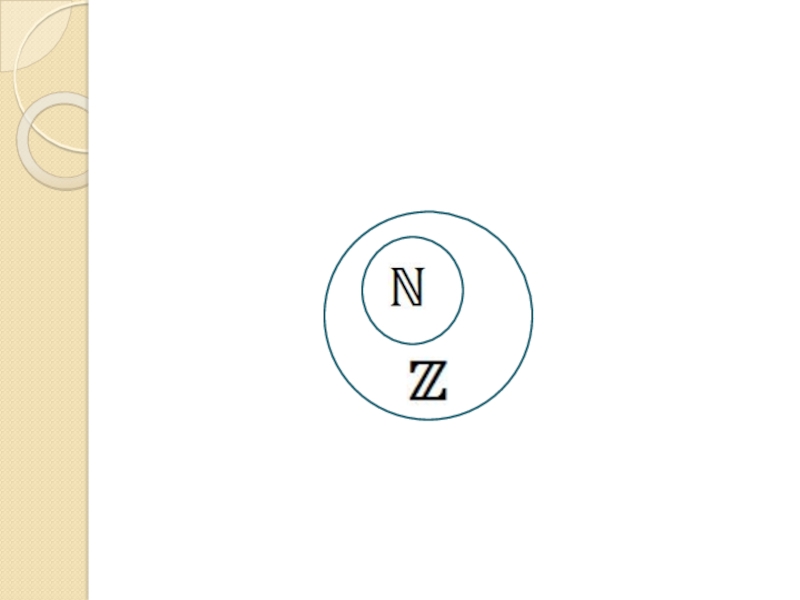
- 5. Натуральные числа 1, 2, 3, 4, 5,
- 7. Целые числа -3, -2, -1, 0, 1,
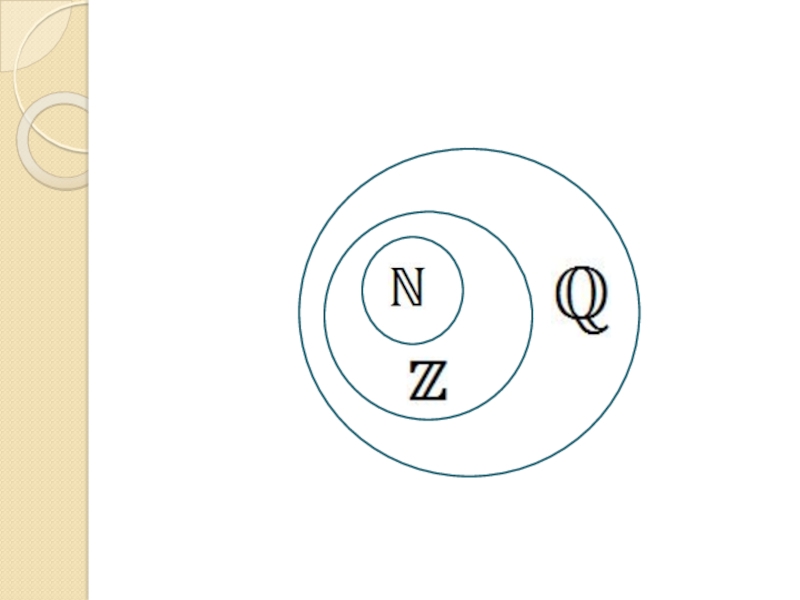
- 9. Рациональные числа 1/2, -3, -5/6, 0, 5,
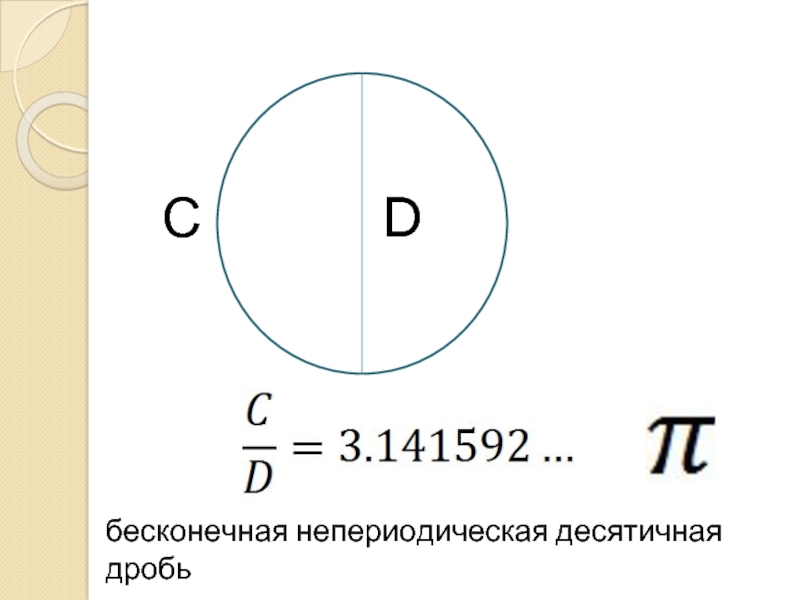
- 11. С D бесконечная непериодическая десятичная дробь
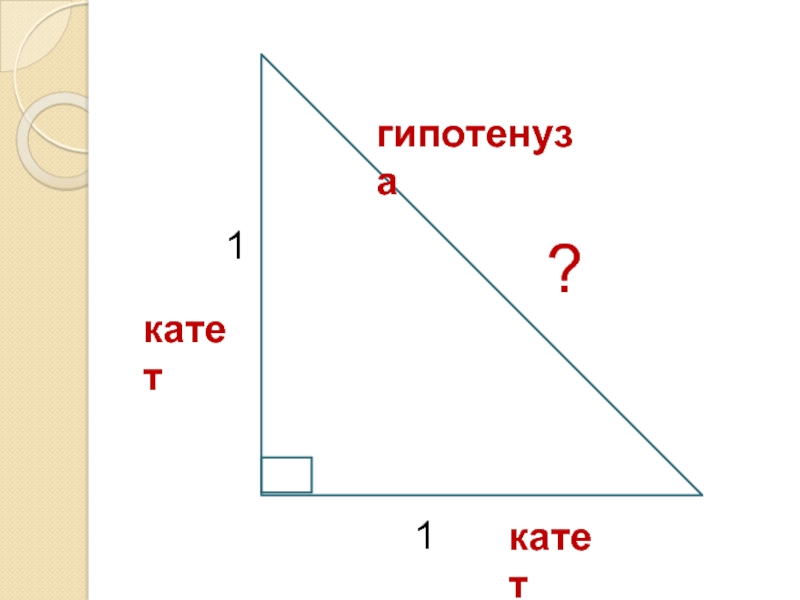
- 12. 1 1 ? катет катет гипотенуза
- 13. Теорема Пифагора В прямоугольном треугольнике квадрат гипотенузы
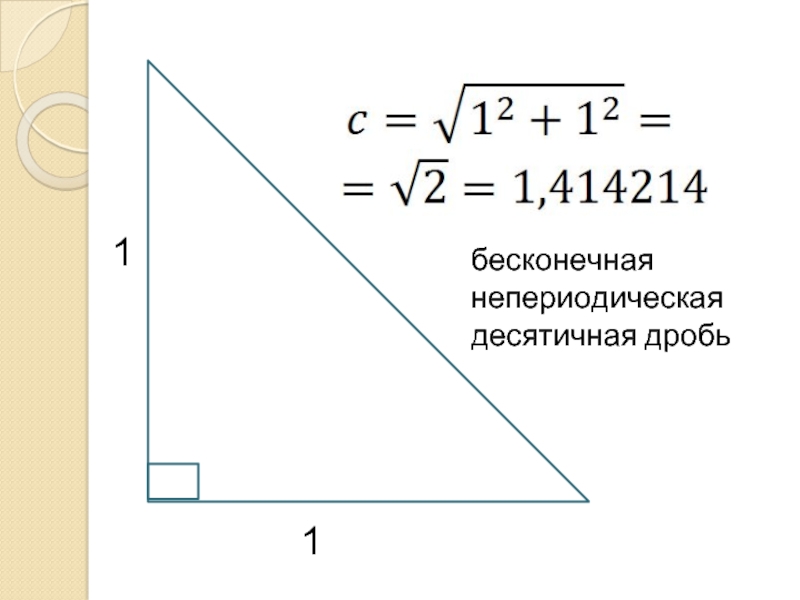
- 14. 1 1 бесконечная непериодическая десятичная дробь
- 15. Иррациональные числа Бесконечные непериодические десятичные дроби
- 16. Действительные числа Рациональные числа + иррациональные от лат. realis —
- 18. Квадратное уравнение x2+x+1=0 ax2+bx+c=0 a,b,c − коэффициенты
- 19. Квадратное уравнение x2+x+1=0 a = 1, b
- 20. Джироламо Кардано Итальянский математик, инженер, философ, медик
- 21. Мнимая единица
- 22. Комплексные числа от лат. complex — тесно связанный z =
Множество Многое, мыслимое нами как единое целое Георг Кантор Совокупность элементов, удовлетворяющих какому-либо характеристическому свойству
Слайд 2Множество
Многое, мыслимое нами как единое целое
Георг Кантор
Совокупность элементов, удовлетворяющих какому-либо характеристическому
свойству
Слайд 3Георг Кантор
Немецкий математик
Создатель теории множеств
1904 г − медаль Сильвестра Лондонского королевского
общества
1845 − 1918
«Никто не изгонит нас из рая, который основал Кантор»
Давид Гильберт
Слайд 4Пример
Множество студентов группы
Множество людей в аудитории
Множество бутылок в ближайшем магазине
Множество атомов
Вселенной
Множество натуральных чисел
Множество натуральных чисел
Слайд 5Натуральные числа
1, 2, 3, 4, 5, …
Числа, используемые для счёта в
природе
от лат. naturalis — естественный
= {1, 2, 3, 4, 5, …}
от лат. naturalis — естественный
= {1, 2, 3, 4, 5, …}
Слайд 9Рациональные числа
1/2, -3, -5/6, 0, 5, …
от лат. quotient — отношение
целые числа
конечные
десятичные дроби
бесконечные периодические десятичные дроби
бесконечные периодические десятичные дроби
Слайд 13Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
a
b
c
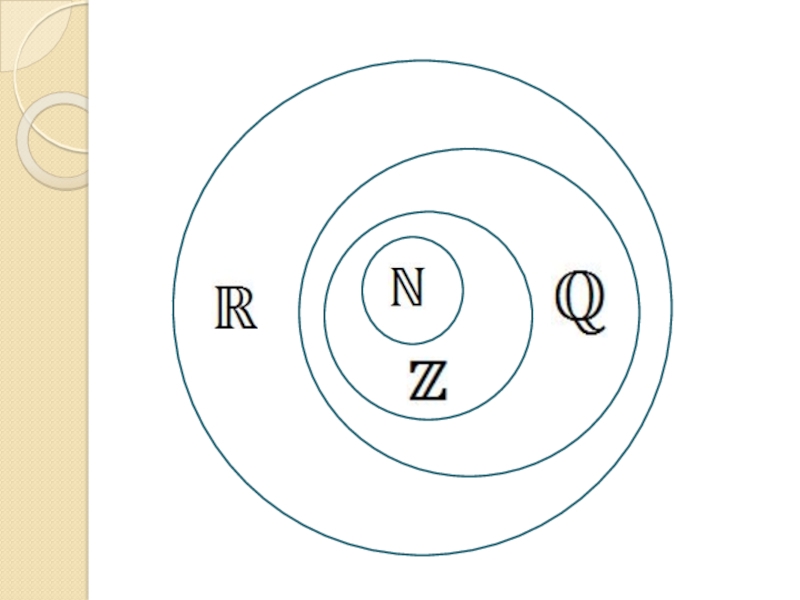
Слайд 16Действительные числа
Рациональные числа + иррациональные
от лат. realis — действительный
Действительные = вещественные
Слайд 19Квадратное уравнение
x2+x+1=0
a = 1, b = 1, c = 1
D =
12 – 4∙1 ∙ 1 = -3 < 0
Арифметический квадратный корень не извлекается из отрицательных чисел
Арифметический квадратный корень не извлекается из отрицательных чисел
Слайд 20Джироламо Кардано
Итальянский математик, инженер, философ, медик и астролог
В его честь −
формулы решения кубического уравнения, карданов подвес и карданный вал
1501 − 1576
1545 г. − Великое искусство, или об алгебраических правилах
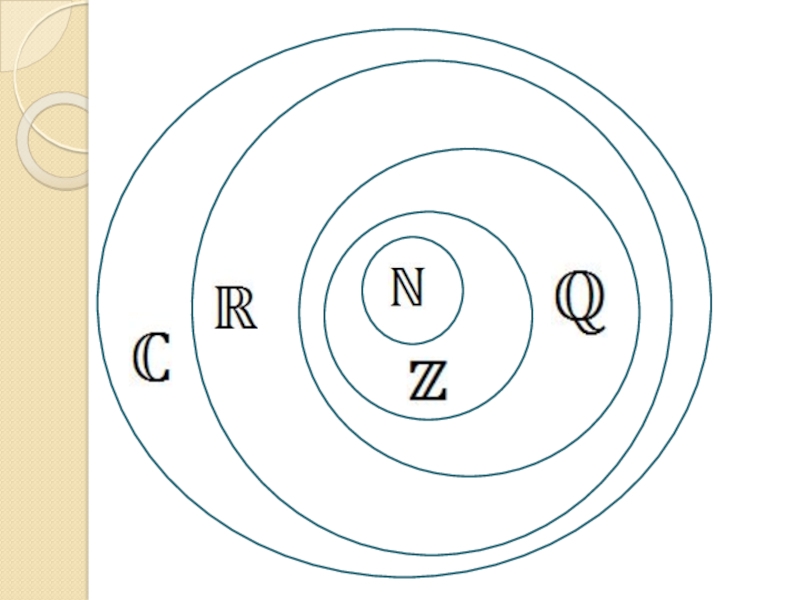
Слайд 22Комплексные числа
от лат. complex — тесно связанный
z = a + bi
Действительная часть
Re(z) = a
Мнимая
часть
Im(z) = b
Im(z) = b
