- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Численное интегрирование презентация
Содержание
- 1. Численное интегрирование
- 2. В каких случаях необходимо использовать численное
- 3. Методы: Численное интегрирование метод прямоугольников;
- 4. Методы прямоугольников метод левых прямоугольников; метод правых прямоугольников; метод средних прямоугольников.
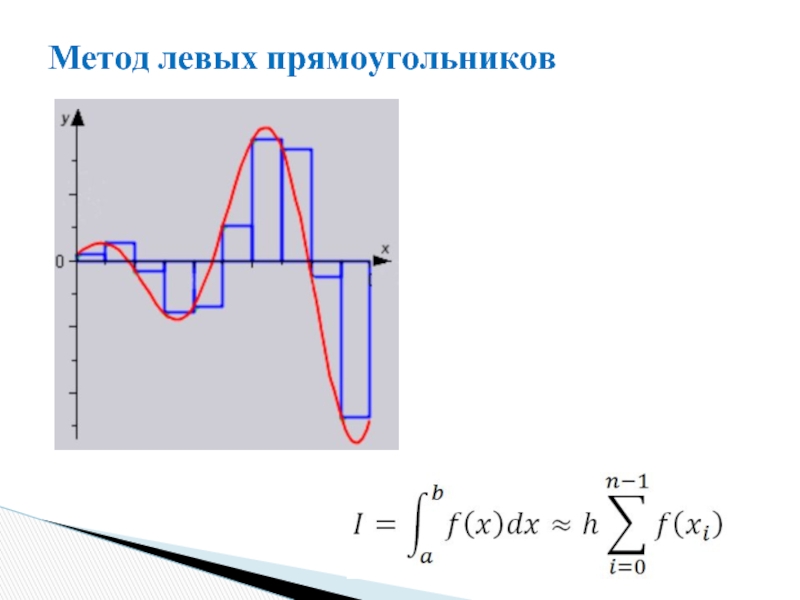
- 5. Метод левых прямоугольников
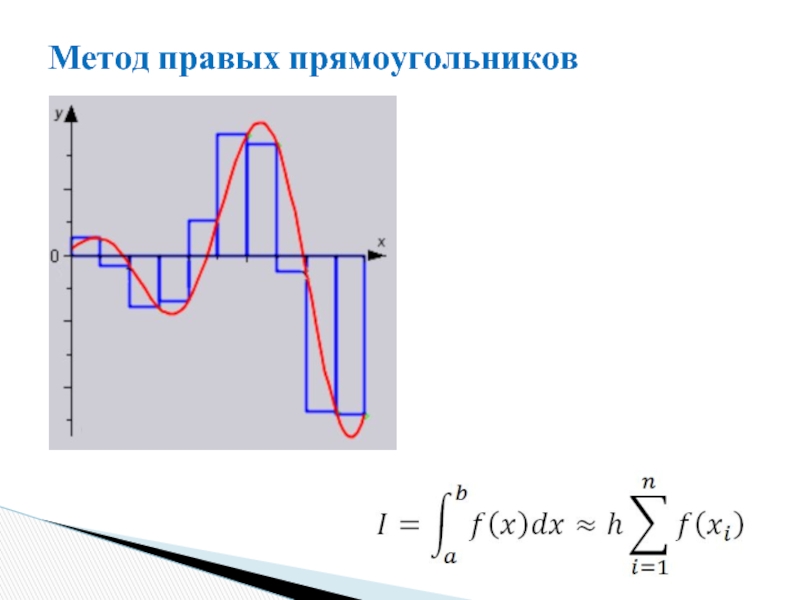
- 6. Метод правых прямоугольников
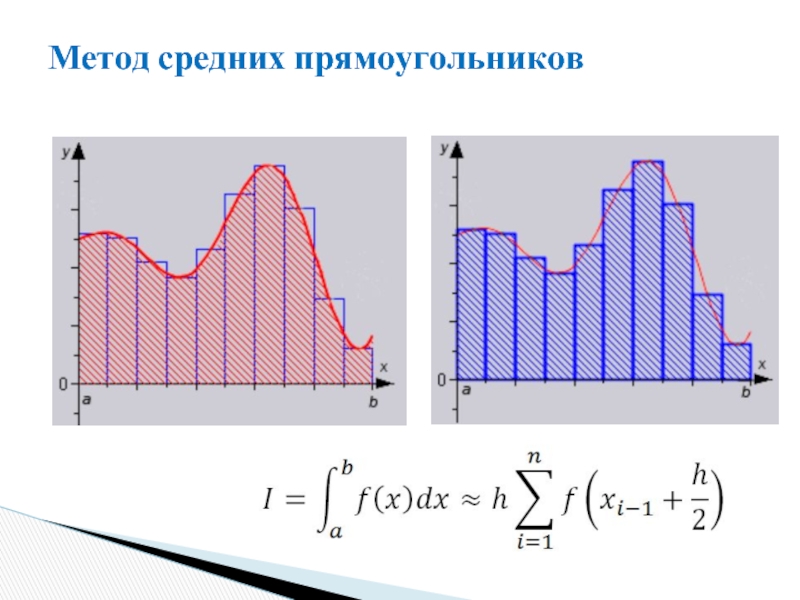
- 7. Метод средних прямоугольников
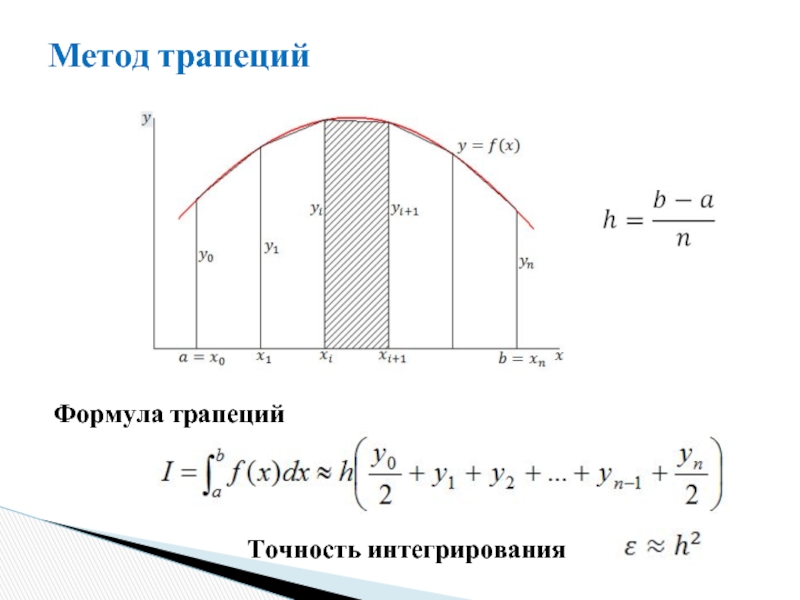
- 8. Метод трапеций Точность интегрирования Формула трапеций
- 9. Метод Симпсона (парабол) Точность интегрирования Количество интервалов Формула Симпсона Площадь параболы
- 10. Метод Гаусса – относительные координаты узлов;
- 11. Метод Гаусса – корни полиномов Лежандра; Вычисление Полиномы Лежандра
- 12. Метод Гаусса Весовые коэффициенты Правые
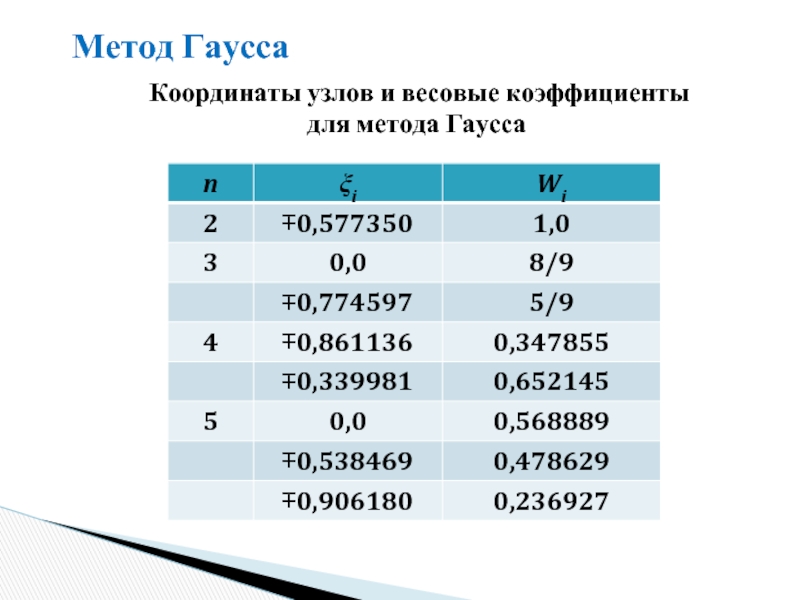
- 13. Метод Гаусса Координаты узлов и весовые коэффициенты для метода Гаусса
- 14. Вычисление интеграла с автоматическим выбором шага интегрирования
- 15. Вычисление несобственных интегралов Алгоритм 1. Задание начального
- 16. Вычисление несобственных интегралов Для вычисления несобственного интеграла
- 17. Задание Вычислить значение интеграла в MathCAD. Написать
- 18. Контрольные вопросы 1. Алгоритмы численного интегрирования (методы
- 19. Спасибо за внимание!
Слайд 2В каких случаях необходимо
использовать численное интегрирование?
интеграл не вычисляется аналитически;
подынтегральная
подынтегральная функция задана таблично.
Слайд 3Методы:
Численное интегрирование
метод прямоугольников;
метод трапеций;
метод Симпсона (парабол);
метод Гаусса.
В основе численных методов
Вычисление интегралов с заданной точностью (автоматическим выбором шага интегрирования).
Вычисление несобственных интегралов.
Вычисление кратных интегралов.
Слайд 4Методы прямоугольников
метод левых прямоугольников;
метод правых прямоугольников;
метод средних прямоугольников.
Слайд 9Метод Симпсона (парабол)
Точность интегрирования
Количество интервалов
Формула Симпсона
Площадь параболы
Слайд 10Метод Гаусса
– относительные координаты узлов;
– весовые коэффициенты.
Квадратурная формула Гаусса
Значения и подбираются так, чтобы формула была точна для всех многочленов степени 2n – 1.
Квадратурная формула Гаусса обеспечивает очень высокую точность при небольшом числе узлов.
Слайд 12Метод Гаусса
Весовые коэффициенты
Правые части
Метод Гаусса можно использовать для вычисления
Демидович Б.П. Марон И.А. Основы вычислительной математики, с. 597
Слайд 14Вычисление интеграла с автоматическим выбором шага интегрирования
1. Начальное значение шага интегрирования
2. Вычисление значения интеграла In с шагом h.
3. Значение шага h делится пополам и вычисление интеграла I2n ведется для шага h/2.
4. Если разность | In - I2n | < ɛ, то значение считается значением I2n интеграла, вычисленным с точностью ɛ.
Если разность | In - I2n | > ɛ, то продолжают деление шага и вычисляют значения I4n, I8n и т. д.
Слайд 15Вычисление несобственных интегралов
Алгоритм
1. Задание начального значения b.
2. Вычисление значения интеграла Ib
3. Значение верхнего предела интегрирования увеличивается вдвое и вычисление интеграла I2b .
4. Если разность | Ib - I2b | < ɛ/2, то значение считается значением I2b несобственного интеграла, вычисленного с точностью ɛ.
Если разность | Ib - I2b | > ɛ/2, то продолжают деление шага и вычисляют значения I4b, I8b и т. д.
f(x) непрерывна на a≤x≤∞
Слайд 16Вычисление несобственных интегралов
Для вычисления несобственного интеграла лучше всего использовать метод Гаусса,
Слайд 17Задание
Вычислить значение интеграла в MathCAD.
Написать программу для вычисления интеграла с использованием
Написать программу для вычисления интеграла с использованием метода Симпсона.
Написать программу для вычисления интеграла с использованием метода Гаусса.
Написать программу для вычисления интеграла с заданной точностью*.
Написать программу для вычисления несобственного интеграла*.
Слайд 18Контрольные вопросы
1. Алгоритмы численного интегрирования (методы прямоугольников, трапеций, Симпсона и Гаусса).
2. Вывод формул для методов трапеций и Симпсона.
3. Виды погрешностей при вычислении интегралов.
4. Алгоритм вычисления интеграла с автоматическим выбором шага интегрирования.
5*. Программа вычисления интеграла с автоматическим выбором шага интегрирования.
6. Алгоритм вычисления несобственного интеграла.
7*. Программа вычисления несобственного интеграла.
8. Численное и аналитическое вычисление интегралов в системе MathCAD.