- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Четырехугольник презентация
Содержание
- 1. Четырехугольник
- 2. Определение Четырёхугольником называется фигура, которая состоит из
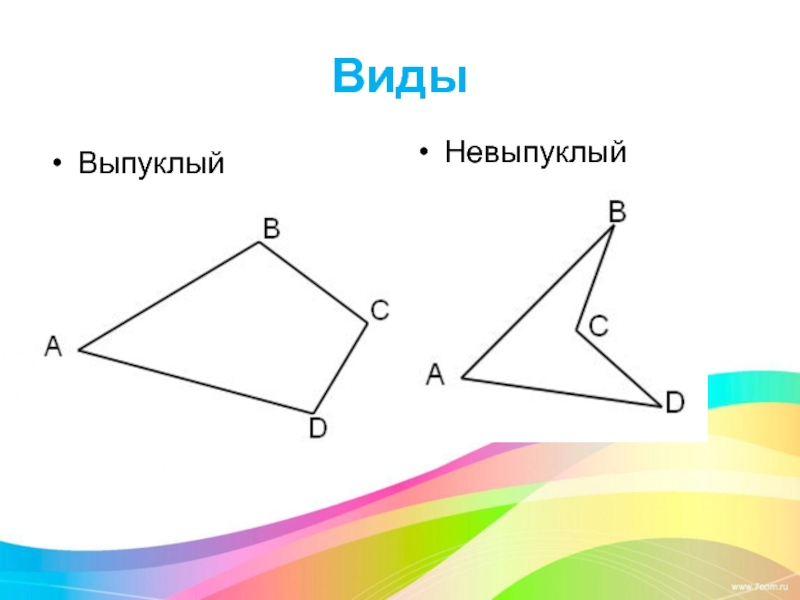
- 3. Виды Выпуклый Невыпуклый
- 4. Четырёхугольник называется выпуклым, если он расположен
- 5. Виды четырехугольника
- 6. Параллелограмм Параллелограммом называется четырёхугольник, противолежащие стороны
- 7. Диагонали параллелограмма пересекаются и точкой пересечения делятся
- 8. Признаки параллелограмма: Если у четырёхугольника противолежащие стороны
- 9. Ромб
- 10. Ромбом называется параллелограмм, у которого все стороны
- 11. Прямоугольник
- 12. Прямоугольником называется параллелограмм, у которого все углы прямые: ∠A=∠B=∠C=∠D=90°.
- 13. Диагонали прямоугольника равны и точкой пересечения делятся
- 14. Квадрат
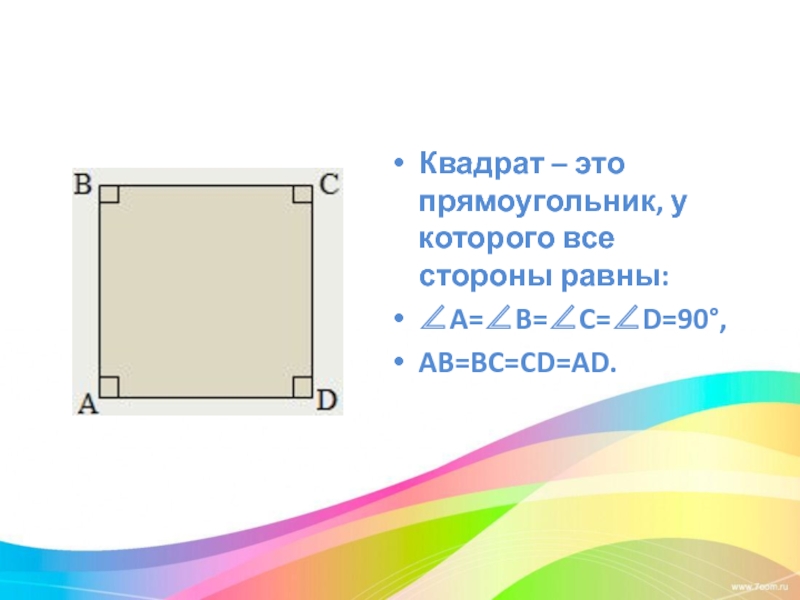
- 15. Квадрат – это прямоугольник, у которого все стороны равны: ∠A=∠B=∠C=∠D=90°, AB=BC=CD=AD.
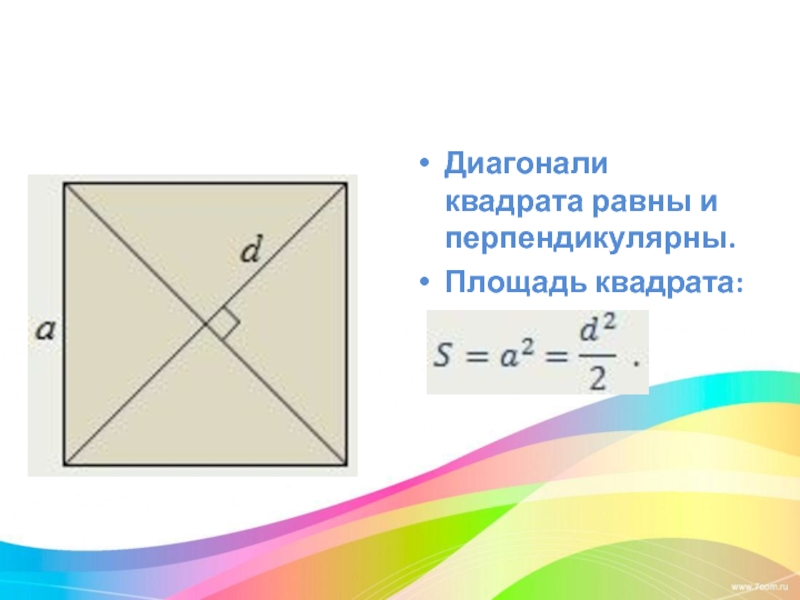
- 16. Диагонали квадрата равны и перпендикулярны. Площадь квадрата:
- 17. Трапеция
- 18. Трапецией называется четырёхугольник у которого только две
- 19. Средней линией (первой средней линией) трапеции называется
- 20. Трапеция называется прямоугольной, если одна из её боковых сторон перпендикулярна основаниям.
- 21. Применение знаний о четырёхугольнике
- 22. В физике применяют параллелограмм при изучении
- 23. Прямоугольник несёт красоту, чёткость, стройность. Стены,
- 24. Ни наука, ни техника, без меня не
- 25. Ромб не имеет большого хозяйственного значения, зато
Слайд 2Определение
Четырёхугольником называется фигура, которая состоит из четырёх точек (вершин) и четырёх
отрезков (сторон), которые последовательно соединяют вершины.
При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.
1. На одной прямой должно лежать не более двух точек.
2. Отрезки, соединяющие точки, не должны пересекаться.
При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.
1. На одной прямой должно лежать не более двух точек.
2. Отрезки, соединяющие точки, не должны пересекаться.
Слайд 4
Четырёхугольник называется выпуклым, если он расположен в одной полуплоскости относительно прямой,
которая содержит любую из его сторон.
Сумма углов выпуклого четырёхугольника равна 360°:
∠A+∠B+∠C+∠D=360°.
Сумма углов выпуклого четырёхугольника равна 360°:
∠A+∠B+∠C+∠D=360°.
Диагоналями четырёхугольника называются отрезки, соединяющие его противолежащие вершины.
Диагонали выпуклого четырёхугольника пересекаются, а невыпуклого – нет.
Слайд 6Параллелограмм
Параллелограммом называется четырёхугольник, противолежащие стороны которого попарно параллельны:
AB||CD, BC||AD.
У параллелограмма
противолежащие стороны равны и противолежащие углы равны:
AB=CD, BC=AD;
∠A=∠C, ∠B=∠D.
Сумма любых двух соседних углов параллелограмма равна 180°:
∠A+∠B=∠B+∠C=∠C+∠D=∠A+∠D=180°.
AB=CD, BC=AD;
∠A=∠C, ∠B=∠D.
Сумма любых двух соседних углов параллелограмма равна 180°:
∠A+∠B=∠B+∠C=∠C+∠D=∠A+∠D=180°.
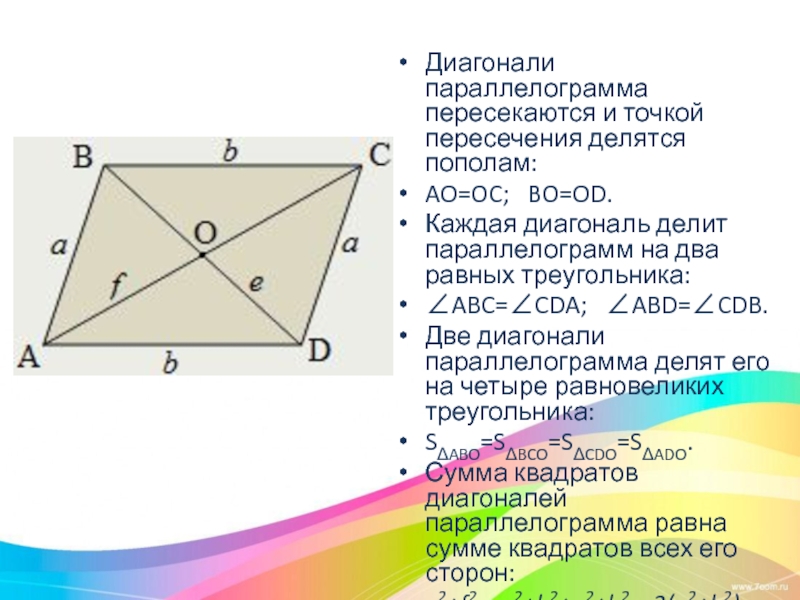
Слайд 7Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам:
AO=OC; BO=OD.
Каждая диагональ делит
параллелограмм на два равных треугольника:
∠ABC=∠CDA; ∠ABD=∠CDB.
Две диагонали параллелограмма делят его на четыре равновеликих треугольника:
SΔABO=SΔBCO=SΔCDO=SΔADO.
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
e2+f2 = a2+b2+a2+b2 = 2(a2+b2).
∠ABC=∠CDA; ∠ABD=∠CDB.
Две диагонали параллелограмма делят его на четыре равновеликих треугольника:
SΔABO=SΔBCO=SΔCDO=SΔADO.
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
e2+f2 = a2+b2+a2+b2 = 2(a2+b2).
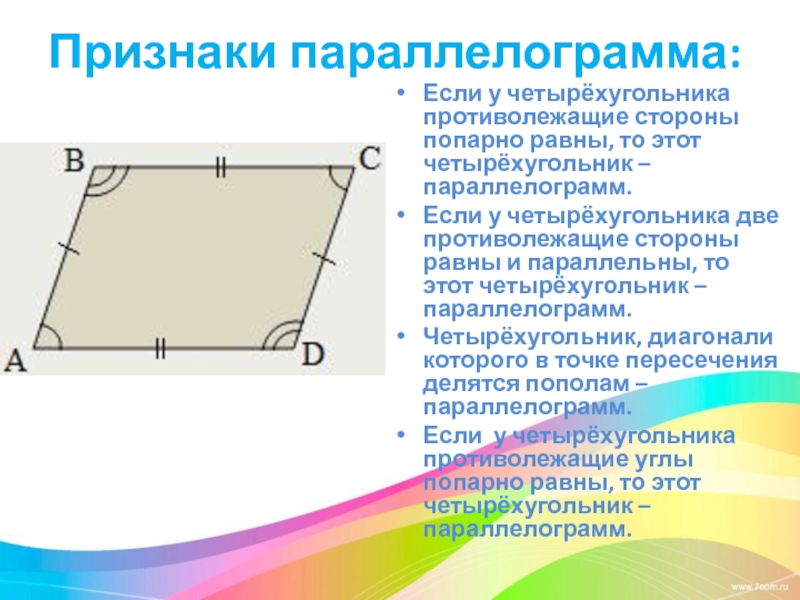
Слайд 8Признаки параллелограмма:
Если у четырёхугольника противолежащие стороны попарно равны, то этот четырёхугольник
– параллелограмм.
Если у четырёхугольника две противолежащие стороны равны и параллельны, то этот четырёхугольник – параллелограмм.
Четырёхугольник, диагонали которого в точке пересечения делятся пополам – параллелограмм.
Если у четырёхугольника противолежащие углы попарно равны, то этот четырёхугольник – параллелограмм.
Если у четырёхугольника две противолежащие стороны равны и параллельны, то этот четырёхугольник – параллелограмм.
Четырёхугольник, диагонали которого в точке пересечения делятся пополам – параллелограмм.
Если у четырёхугольника противолежащие углы попарно равны, то этот четырёхугольник – параллелограмм.
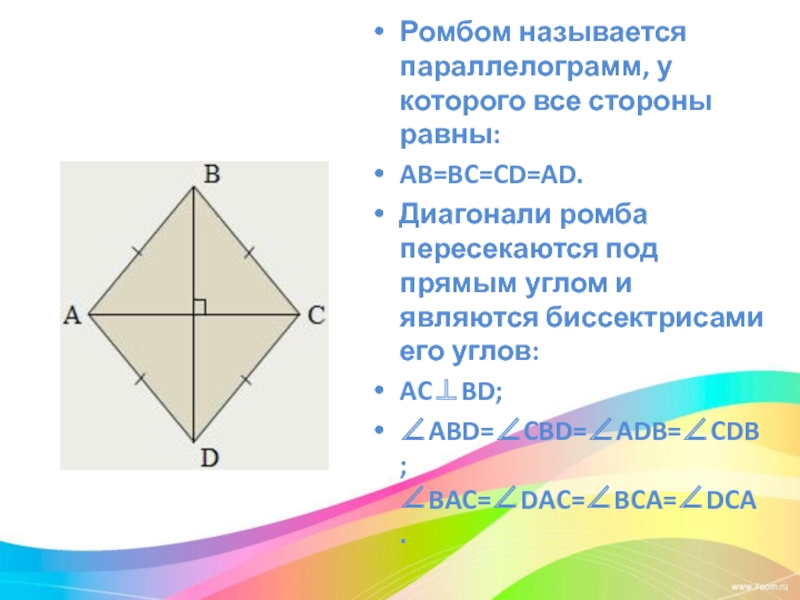
Слайд 10Ромбом называется параллелограмм, у которого все стороны равны:
AB=BC=CD=AD.
Диагонали ромба пересекаются под
прямым углом и являются биссектрисами его углов:
AC⊥BD;
∠ABD=∠CBD=∠ADB=∠CDB; ∠BAC=∠DAC=∠BCA=∠DCA.
AC⊥BD;
∠ABD=∠CBD=∠ADB=∠CDB; ∠BAC=∠DAC=∠BCA=∠DCA.
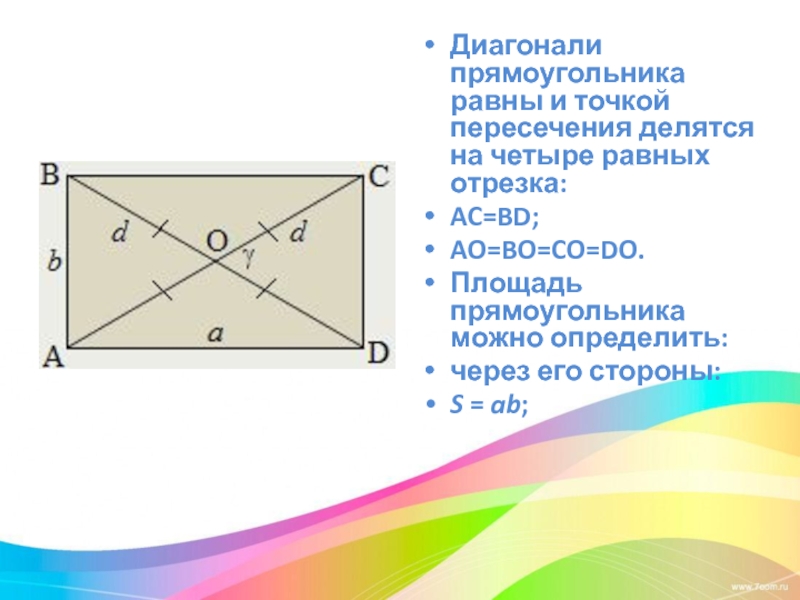
Слайд 13Диагонали прямоугольника равны и точкой пересечения делятся на четыре равных отрезка:
AC=BD;
AO=BO=CO=DO.
Площадь
прямоугольника можно определить:
через его стороны:
S = ab;
через его стороны:
S = ab;
Слайд 18Трапецией называется четырёхугольник у которого только две противолежащие стороны параллельны:
AD||BC.
Параллельные стороны
называются основаниями трапеции, непараллельные – боковыми сторонами.
Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.
Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.
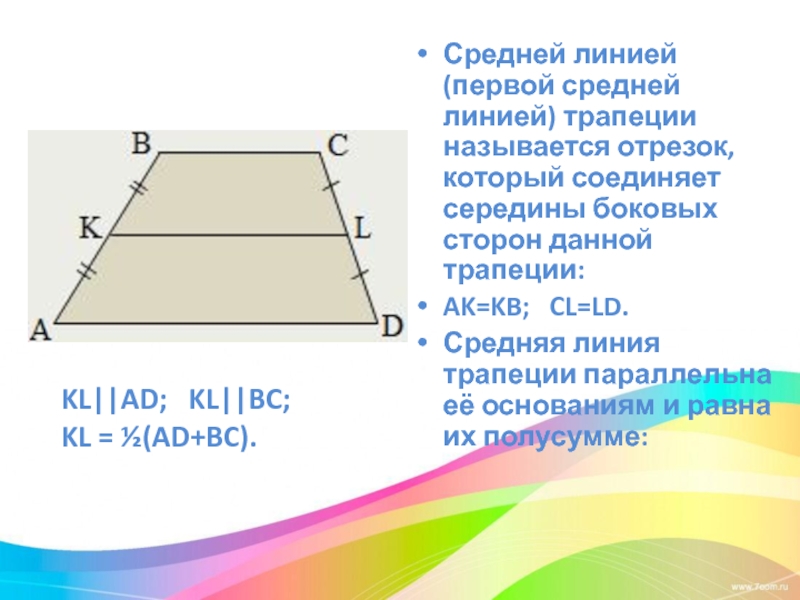
Слайд 19Средней линией (первой средней линией) трапеции называется отрезок, который соединяет середины
боковых сторон данной трапеции:
AK=KB; CL=LD.
Средняя линия трапеции параллельна её основаниям и равна их полусумме:
AK=KB; CL=LD.
Средняя линия трапеции параллельна её основаниям и равна их полусумме:
KL||AD; KL||BC;
KL = ½(AD+BC).
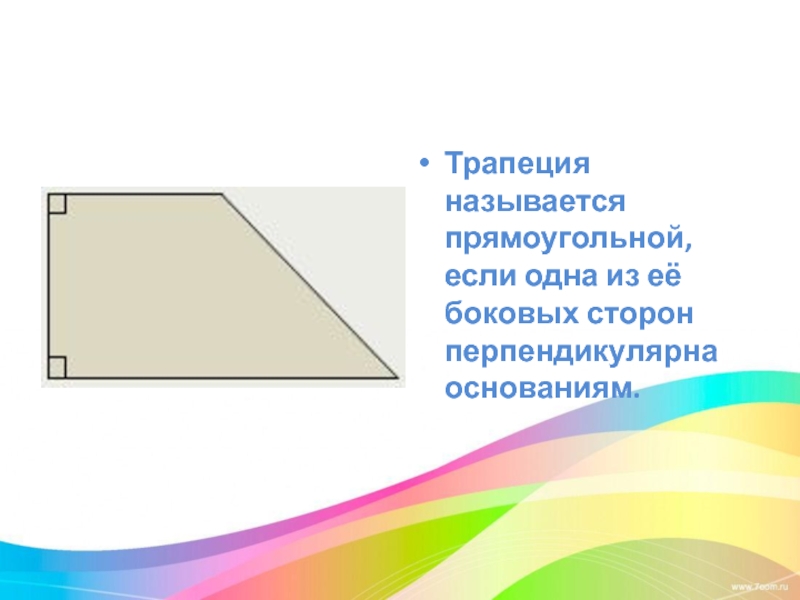
Слайд 20
Трапеция называется прямоугольной, если одна из её боковых сторон перпендикулярна основаниям.
Слайд 22В физике применяют параллелограмм при изучении сил, при нахождении равнодействующей силы.
В жизни параллелограмм – это рамы велосипедов, мотоциклов, где для жёсткости проведена диагональ.
Слайд 23Прямоугольник несёт красоту, чёткость, стройность.
Стены, пол, потолок, поверхность стола, футбольное
поле, грани карандашей, даже записная книжка – все это прямоугольники.
Попробуйте построить дом или сделать раму для картины, не зная свойств прямоугольника.
Попробуйте построить дом или сделать раму для картины, не зная свойств прямоугольника.
Слайд 24Ни наука, ни техника, без меня не обходятся.
И в хозяйственных
делах я тоже используюсь.
В основании мраморных колонн лежит квадрат.
Ваши товарищи, играя в шахматы, фигуры по квадратам передвигают.
А как меня ребятишки любят! Тетрадки у них разрисованы голубыми квадратиками.
В хирургическом отделении для пересадки кожи применяют специальную машинку, которая вырезает кожу в виде квадратов. Их располагают на обожжённом участке в шахматном порядке.
В сельском хозяйстве применяют квадратно- гнездовой способ посадки и т.д.
В основании мраморных колонн лежит квадрат.
Ваши товарищи, играя в шахматы, фигуры по квадратам передвигают.
А как меня ребятишки любят! Тетрадки у них разрисованы голубыми квадратиками.
В хирургическом отделении для пересадки кожи применяют специальную машинку, которая вырезает кожу в виде квадратов. Их располагают на обожжённом участке в шахматном порядке.
В сельском хозяйстве применяют квадратно- гнездовой способ посадки и т.д.
Слайд 25Ромб не имеет большого хозяйственного значения, зато используются в искусстве.
Любят рисовать
на тканях художники, используют в узорах ковровщицы.
Плиточники укладывают плитки в виде ромба,– из них получаются красивые узоры.
Реечный домкрат для легковых автомобилей также имеет форму ромба.
Плиточники укладывают плитки в виде ромба,– из них получаются красивые узоры.
Реечный домкрат для легковых автомобилей также имеет форму ромба.