- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Cálculo numérico. Integração Numérica. (Aula 8) презентация
Содержание
- 1. Cálculo numérico. Integração Numérica. (Aula 8)
- 2. CONTEÚDO PROGRAMÁTICO DESTA AULA Integração Numérica: Método de Romberg – 10 passo Extrapolação de Richardson.
- 3. INTEGRAÇÃO NUMÉRICA – CONTINUAÇÃO
- 4. MÉTODO
- 5. MÉTODO
- 6. MÉTODO
- 7. MÉTODO
- 8. MÉTODO
- 9. EXEMPLO1: Utilize a Regra do Trapézio Repetida
- 10. EXEMPLO1 – CONTINUAÇÃO
- 11. EXEMPLO1 – CONTINUAÇÃO
- 12. EXEMPLO1 – CONTINUAÇÃO
- 13. EXEMPLO1 – CONTINUAÇÃO
- 14. EXTRAPOLAÇÃO DE RICHARDSON
- 15. TABELA DE ROMBERG
- 16. EXEMPLO2: Utilize o método de Romberg para
- 17. EXEMPLO2 - CONTINUAÇÃO
- 18. EXEMPLO2 - CONTINUAÇÃO
- 19. RESUMINDO Nesta aula vocês estudaram: Integração
CONTEÚDO PROGRAMÁTICO DESTA AULA Integração Numérica: Método de Romberg – 10 passo Extrapolação de Richardson.
Слайд 2CONTEÚDO PROGRAMÁTICO DESTA AULA
Integração Numérica:
Método de Romberg – 10 passo
Extrapolação de
Richardson.
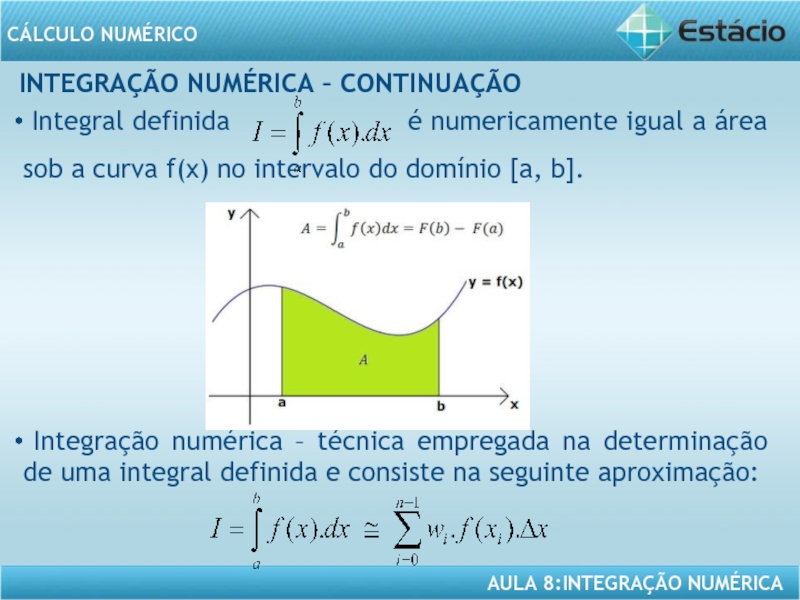
Слайд 3INTEGRAÇÃO NUMÉRICA – CONTINUAÇÃO
Integral definida
é numericamente igual a área sob a curva f(x) no intervalo do domínio [a, b].
Integração numérica – técnica empregada na determinação de uma integral definida e consiste na seguinte aproximação:
Integração numérica – técnica empregada na determinação de uma integral definida e consiste na seguinte aproximação:
Слайд 4
MÉTODO DE ROMBERG
O método de Romberg consiste na sucessiva aplicação da
extrapolação de Richardson à quadratura do trapézio composta o que resulta em uma quadratura composta de maior exatidão.
Onde:
Onde:
Слайд 5
MÉTODO DE ROMBERG - CONTINUAÇÃO
É possível demonstrar que a determinação de
I é dada aproximadamente por:
Onde:
ATENÇÃO!
Na expressão anterior, quando k = 1, temos que o limite superior será 0, o que significa que não há termo a ser adicionado.
Onde:
ATENÇÃO!
Na expressão anterior, quando k = 1, temos que o limite superior será 0, o que significa que não há termo a ser adicionado.
Слайд 6
MÉTODO DE ROMBERG - CONTINUAÇÃO
A partir de agora será introduzida a
notação de ROMBERG Rk,1.
k = 1
k = 2
k = 1
k = 2
Слайд 8
MÉTODO DE ROMBERG - CONTINUAÇÃO
Reescrevendo R3,1 em função de R2,1, temos:
Generalizando,
temos que:
ATENÇÃO!
Este é o primeiro passo do método de Romberg – aproximações via regra dos trapézios
ATENÇÃO!
Este é o primeiro passo do método de Romberg – aproximações via regra dos trapézios
Слайд 9EXEMPLO1: Utilize a Regra do Trapézio Repetida para realizar o primeiro
passo do esquema da integração de Romberg para obter uma aproximação da integral
para k = 1, 2, ..., 5
para k = 1, 2, ..., 5
SOLUÇÃO: Determinação dos Rk,1:
k = 1 ⇒
Слайд 13EXEMPLO1 – CONTINUAÇÃO
k = 5 ⇒ R5,1 = 1,99357034
k
= 6 ⇒ R6,1 = 1,99839336
Valor exato:
CONVERGÊNCIA LENTA ⇒ extrapolação de Richardson
Valor exato:
CONVERGÊNCIA LENTA ⇒ extrapolação de Richardson
Слайд 14EXTRAPOLAÇÃO DE RICHARDSON
Com o intuito de acelerar a convergência do método
de Romberg, a partir do seu primeiro passo é possível fazer a extrapolação de Richardson e chegar a seguinte fórmula de recorrência.
Слайд 16EXEMPLO2: Utilize o método de Romberg para obter uma aproximação da
integral
Solução:
Tabela de Romberg:
Do exemplo1: R1,1 = 0; R2,1 = 1,57079633 e R3,1 = 1,8961189
Solução:
Tabela de Romberg:
Do exemplo1: R1,1 = 0; R2,1 = 1,57079633 e R3,1 = 1,8961189
Слайд 19RESUMINDO
Nesta aula vocês estudaram:
Integração Numérica:
Método de Romberg – 10 passo
Extrapolação
de Richardson.
