- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Булевы отношения презентация
Содержание
- 1. Булевы отношения
- 2. Декартово произведение
- 3. Пример A={1, 2, 3}, B={r, s}
- 4. Примеры
- 5. Определения Область определения отношения R на А
- 6. С каждым отношением R на A ×
- 7. Примеры Пусть R={(1, r), (1, s), (3,
- 8. Определение Пусть R⊆A×B – отношение на A×B,
- 9. Пример Пусть А={1, 2, 3}, B={x, y},
- 10. поскольку
- 11. Пример Пусть R и S – бинарные
- 12. Теорема Композиция отношений ассоциативна: если A, B,
- 13. Определения Отношение R на A×A называется рефлексивным,
- 14. Пример Пусть А = {1, 2, 3,
- 15. Отношение R1 является транзитивным:
- 16. Пример Пусть А – множество положительных чисел.
- 17. Определения Пусть R – бинарное отношение на
- 18. Теорема Пусть R – отношение на множестве
- 19. Начальные сведения о графах. Подробно в о
- 20. Конечный граф изображается при помощи диаграммы, в
- 21. Пример Граф, в котором множество вершин V={a,
- 22. Определения Ориентированный граф, или орграф G состоит
- 23. В случае ориентированного графа допускается наличие петель.
- 24. Пример Орграф с вершинами V={a,
- 25. Определение Отношение R на А есть отношение
- 26. Пример (*) Пусть С = {1, 2,
- 27. Пример Пусть S – множество действительных чисел,
- 28. Определение Два элемента a и b ЧУ-множества
- 29. Примеры Пусть Т – множество положительных делителей
- 30. Пример Пусть S – множество всех подмножеств
- 31. Диаграммы Гессе Для изображения ЧУ-множеств. Для заданного
- 32. Диаграмма Гессе, соответствующая множеству (Т, ≤1)
- 33. Диаграмма Гессе, соответствующая множеству (S, ≤3)
- 34. Задания для самостоятельной работы 1.
- 35. Отношения эквивалентности
- 36. Определение
- 40. Пример Пусть множество А – набор разноцветных
- 41. Определение Пусть a ∈ A, и R
- 42. Пример Отношение R1 есть отношение эквивалентности на
- 43. Также:
- 44. Имеется только три различных класса эквивалентности:
- 45. Из примера видно, что любой элемент
- 46. Пример Рассмотрим отношение эквивалентности R3 и примера
- 48. представляют собой различные
- 49. Определения Совокупность классов эквивалентности разделяет все множество
- 50. Теорема Непустое множество подмножеств 〈А〉 множества А
- 51. Пример Пусть Рассмотрим разбиение
Слайд 1
Булевы отношения
Лектор: Завьялов Олег Геннадьевич
кандидат физико-математических наук, доцент
Слайд 2Декартово произведение
Отношением R множества А и В называется
Говорят, что a и b находятся в отношении R, или a относится к b.
Если А=В, то отношение есть подмножество А×А; такое отношение называется бинарным отношением (или отношение) на А.
Слайд 3Пример
A={1, 2, 3}, B={r, s}
A×B= {(1,r), (1,s), (2,r), (2,s), (3,r), (3,s)}
Тогда
(3, s)∈R 3Rs
Множество А ×B содержит 6 элементов.
2^6=64 подмножеств множества А ×B
64 различных отношения на А ×B
Слайд 5Определения
Область определения отношения R на А и В есть множество всех
Область определения R есть множество всех первых координат упорядоченных пар из R.
Множество значений отношения R на А и В есть множество всех у ∈В таких, что (х, у) ∈R для некоторого х∈А.
Множество значений R есть множество всех вторых координат упорядоченных пар из R.
Слайд 6С каждым отношением R на A × B связано отношение R
Пусть R ⊆A×B есть отношение на A×B.
Тогда отношение R -1 на В ×А определяется следующим образом:
R -1={(b, a): (a, b) ∈R}.
(b, a) ∈R -1 тогда и только тогда, когда (a, b) ∈R,
что равносильно bR -1a тогда и только тогда, когда aRb.
Отношение R -1 называется обратным отношением к данному отношению R.
Слайд 7Примеры
Пусть R={(1, r), (1, s), (3, s)},
тогда R -1 =
Пусть {(x,y): x - является мужем y},
тогда R -1 – отношение {(x,y): у – жена х}.
Пусть R – отношение {(x,y): y является родственником х},
тогда R = R -1.
Пусть R – отношение {(x,y): х2 + y2 =4},
тогда R = R -1.
Слайд 8Определение
Пусть R⊆A×B – отношение на A×B,
а S⊆B×C – отношение на
Композицией отношений S и R называется отношение T⊆A×C, определенное таким образом:
Т={(a, c): существует такой элемент b из B,
что (a, b)∈R и (b, с)∈S}.
Это множество обозначается Т = S ° R.
Слайд 9Пример
Пусть А={1, 2, 3}, B={x, y}, C=
Пусть отношения R на A
тогда
Слайд 11Пример
Пусть R и S – бинарные отношения на множестве положительных целых
S = {(x, x+2): x – положительное целое число} и
R = {(x, x2): x –положительное целое число} и
R ° S = {(x, (x+2)2): x – положительное целое число}
Слайд 12Теорема
Композиция отношений ассоциативна: если A, B, C и D – множества
Доказательство:
Пусть (a, d) ∈ T ° (S ° R), тогда существует такое с ∈ С, что (a, c) ∈ S ° R и (c, d) ∈ T.
Поскольку (a, c) ∈ S ° R, существует такое b ∈ B, что (a, b) ∈ R и (b, c) ∈ S.
Поскольку (b, c) ∈ S и (c, d) ∈ T, (b, d) ∈ T ° S.
Поскольку (b, d) ∈ T ° S и (a, b) ∈R, (a, d) ∈ (T ° S) ° R.
Таким образом, T ° (S ° R) ⊆ (T ° S) ° R.
Вторая часть доказательства, что (T ° S) ° R ⊆ T ° (S ° R) аналогична.
Слайд 13Определения
Отношение R на A×A называется рефлексивным, если (a, a) принадлежит
Отношение R называется антирефлексивным, если из (a, b) ∈ R следует a ≠ b.
Отношение R симметрично, если для всех a и b, принадлежащих А, из (a, b) ∈ R следует, что (b, a) ∈ R.
Отношение R транзитивно, если для всех a, b и с из А, (a, b) ∈ R и (b, с) ∈ R, следует, что (a, c) ∈ R.
Отношение R называется антисимметричным, если для всех a и b из А, из принадлежности (a, b) и (b, a) отношению R следует, что a=b.
Слайд 14Пример
Пусть А = {1, 2, 3, 4, 5, 6} и пусть
есть множество R1 = {(1,1), (2, 2), (3, 3), (4, 4), (5, 5), (6,6), (1, 2), (1, 4), (2, 1), (2, 4), (3, 5), (5, 3), (4, 1), (4, 2)}.
Отношение R1 рефлексивно, так как для каждого a ∈ A, (a, a) ∈ R1.
Отношение R1 является симметричным:
Слайд 15
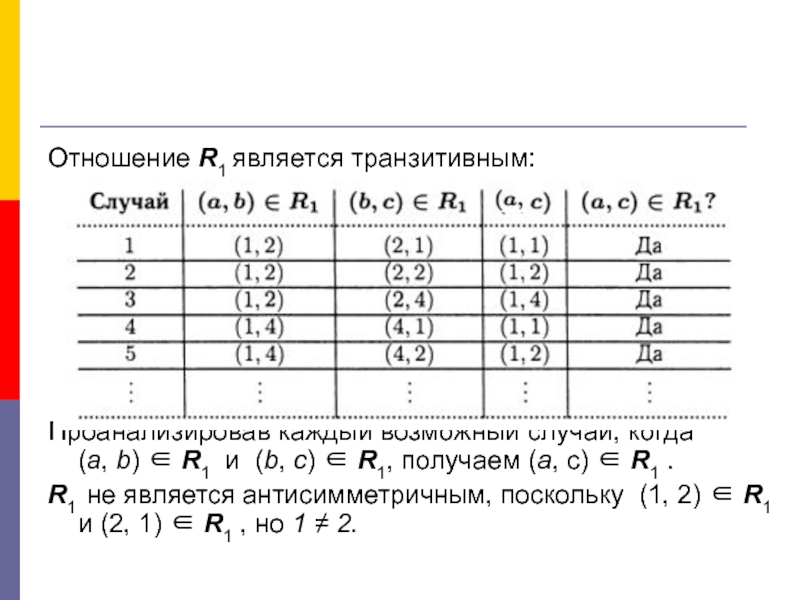
Отношение R1 является транзитивным:
Проанализировав каждый возможный случай, когда
R1 не является антисимметричным, поскольку (1, 2) ∈ R1 и (2, 1) ∈ R1 , но 1 ≠ 2.
Слайд 16Пример
Пусть А – множество положительных чисел.
Отношение R: (x, y) R,
R рефлексивно, т.к. для каждого положительного числа n, n=1 ⋅ n и (n, n) ∈ R.
R не является симметричным, так как (2, 4) ∈ R, но (4, 2) ∉ R.
R антисимметрично, так как если (m, n) ∈ R и (n, m) ∈ R, тогда n кратно m и m кратно n, так что m=n.
R транзитивно, потому что если (m, n) ∈ R и (n, p) ∈ R, тогда n кратно m и p кратно n, так что p кратно m и (m, p) ∈ R.
Слайд 17Определения
Пусть R – бинарное отношение на множестве А.
Рефлексивное замыкание R
Симметричное замыкание R есть наименьшее симметричное отношение на А, содержащее R как подмножество.
Транзитивное замыкание R есть наименьшее транзитивное отношение на А, содержащее R как подмножество.
Слайд 18Теорема
Пусть R – отношение на множестве А и I = {x:
R ∪ I есть рефлексивное замыкание R;
R ∪ R -1 есть симметричное замыкание R;
Если А – конечное множество, содержащее n элементов, то отношение
R ∪ R 2 ∪ R 3 ∪ … ∪ R n есть транзитивное замыкание R.
Слайд 19Начальные сведения о графах. Подробно в о 2 семестре Граф – наглядное
Граф – конечное множество V, называемое множеством вершин, на котором задано симметричное антирефлексивное отношение R и выделено множество Е двухэлементных подмножеств V, определяемое как {a, b} ∈ E тогда и только тогда, когда (a, b) ∈ R и a ≠ b.
Множество Е называется множеством ребер. Всякий элемент Е называется ребром.
Граф обозначается G(V, E).
Элементы a и b графа V соединены или связаны ребром {a, b}, если {a, b} ∈ E.
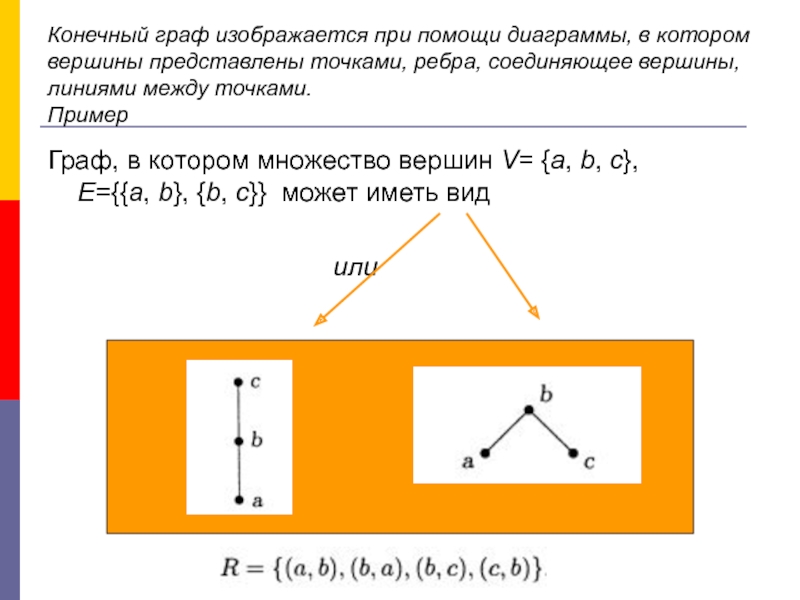
Слайд 20Конечный граф изображается при помощи диаграммы, в котором вершины представлены точками,
Граф, в котором множество вершин V= {a, b, c}, E={{a, b}, {b, c}} может иметь вид
или
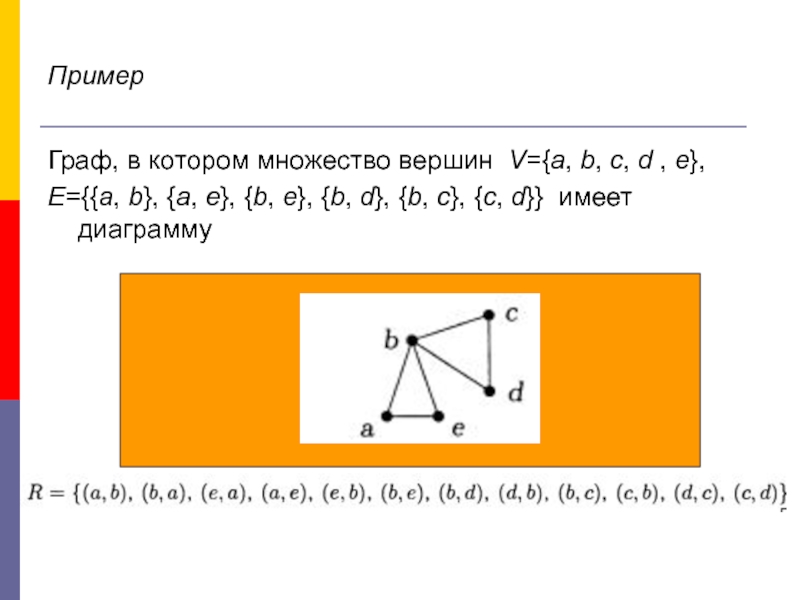
Слайд 21Пример
Граф, в котором множество вершин V={a, b, c, d , e},
Е={{a, b}, {a, e}, {b, e}, {b, d}, {b, c}, {c, d}} имеет диаграмму
Слайд 22Определения
Ориентированный граф, или орграф G состоит из множества V вершин и
Обозначается G(V, E)
Элемент множества Е называется ориентированным ребром.
Если (a, b) ∈ E, тогда a называется начальной вершиной (a, b), b - его конечной вершиной.
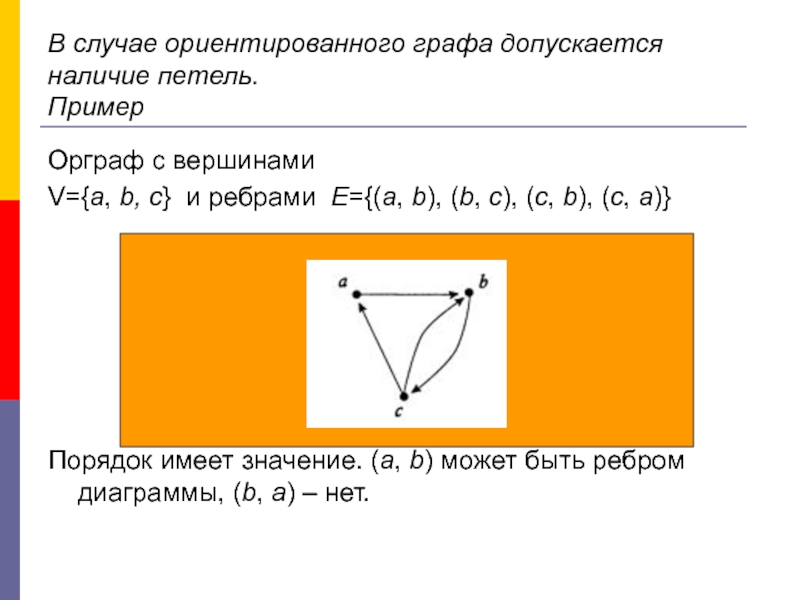
Слайд 23В случае ориентированного графа допускается наличие петель.
Пример
Орграф с вершинами
V={a, b, c}
Порядок имеет значение. (a, b) может быть ребром диаграммы, (b, a) – нет.
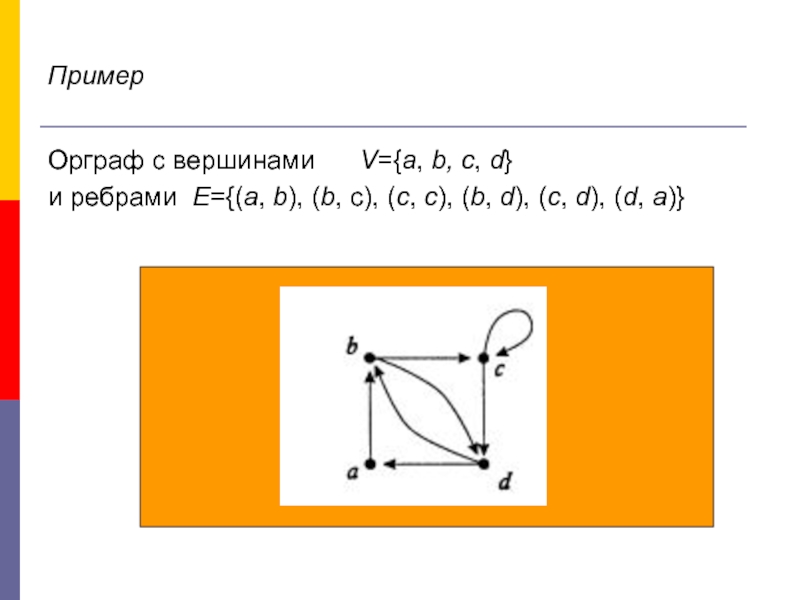
Слайд 24Пример
Орграф с вершинами V={a, b, c, d}
и ребрами
Слайд 25Определение
Отношение R на А есть отношение частичного порядка, если оно рефлексивно,
Если отношение R на А является отношением частичного порядка, то (А, R) называют частично упорядоченным множеством (или ЧУ-множеством с порядком R).
Если отношение порядка R предполагается по умолчанию, то (А, R) можно обозначить просто через А.
Слайд 26Пример (*)
Пусть С = {1, 2, 3}, Х – множество всех
Определим отношение R на Х посредством (T, V) ∈ R, если T ⊆ V.
({2}, {1, 2}) ∈ R, поскольку {2} ⊆ {1, 2} и
({1, 2}, {3}) ∉ R, поскольку {2, 3} ⊄ {3}.
R – отношение частичного порядка,
(A, R) – ЧУ-множество.
Слайд 27Пример
Пусть S – множество действительных чисел,
R1 – отношение, определенное условием
R1 – отношение частичного порядка,
(S, R1) – ЧУ-множество.
Обозначение.
Частично упорядочение принято обозначать через ≤
а ЧУ-множество - через (S, ≤).
≤ -частичный порядок на множестве S.
Слайд 28Определение
Два элемента a и b ЧУ-множества (S, ≤) сравнимы, если a
Если каждые два элемента ЧУ-множества (S, ≤) сравнимы, то (S, ≤) называется вполне упорядоченным множеством, или цепью.
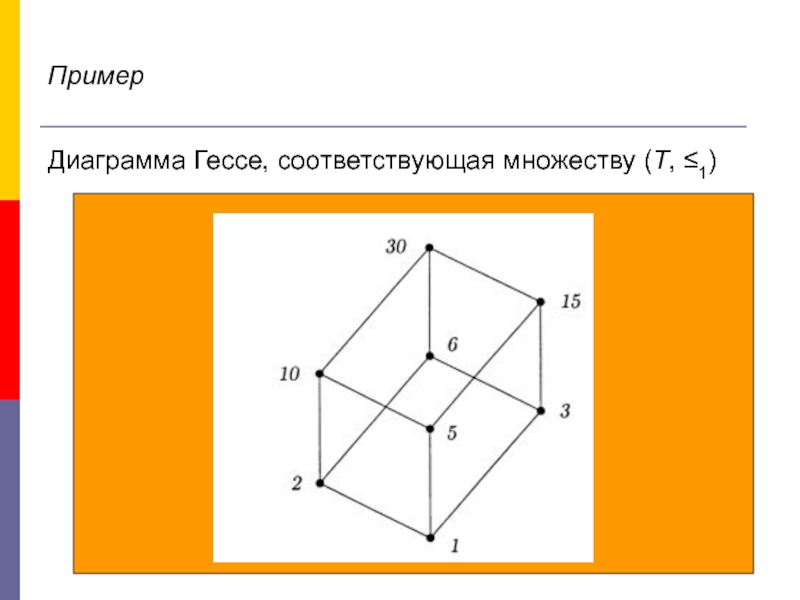
Слайд 29Примеры
Пусть Т – множество положительных делителей числа 30 и ≤1 есть
Пусть А – множество целых чисел и
R= ≤2 – отношение х ≤2 у, если х меньшее или равно у. Упорядоченное множество (А, ≤2) является цепью.
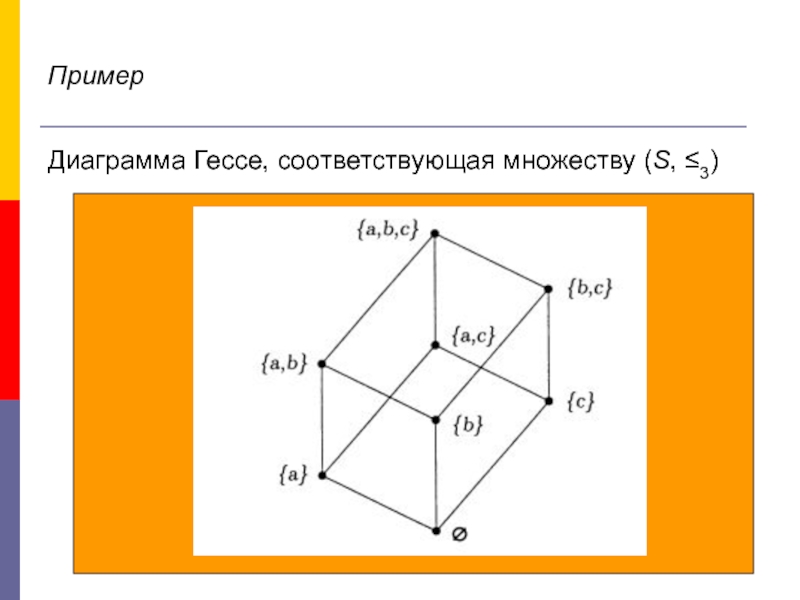
Слайд 30Пример
Пусть S – множество всех подмножеств множества
{a,b,c} ≤3 есть отношение
примере (*).
Множества {a, b} и {a,b,c} сравнимы,
однако {a, b} и {b,c} таковыми не являются.
ЧУ-множество (S, ≤3) цепью не является.
Слайд 31Диаграммы Гессе
Для изображения ЧУ-множеств.
Для заданного ЧУ-множества (А, ≤2) диаграмма Гессе состоит
Если рассмотрение отношений ограничено отношениями частичного порядка, для них диаграммы Гессе – просто ориентированный граф, в котором петли не указаны.
Если a ≤ b ≤ c, тогда линия от a к с не указана.
Слайд 36Определение
Отношение R
если оно рефлексивно, симметрично и транзитивно,
Пример (**).
Пусть А – множество целых чисел.
Отношение R3 ⊆ А × А посредством R3 ={(a, b): a – b = 5⋅k
для некоторого числа k}.
Например, (7,2) ∈ R3 , т.к. 7 – 2 = 5 = 5 ⋅ 1,
(-11, 4) ∈ R3 , т.к. (-11) – 4 = -15 = 5 ⋅ (-3)
Слайд 37
Отношение R3
Если а – целое число (а ∈ А), то a – a = 0 = 5 ⋅ 0 = 5 ⋅ k
для k = 0. ⇒ (а, а) ∈ R3 .
Отношение R3 симметрично.
(a, b) ∈ R3 . Тогда существует целое m, что a – b = 5 ⋅ m
для m – целого. ⇒ (b, a) ∈ R3
Слайд 38
Отношение R3
Предположим, a, b, c – целые числа,
(a, b) ∈ R3 и (b, c) ∈ R3 .
Если (a, b) ∈ R3 , тогда a – b = 5 ⋅ k для некоторого
целого числа k,
Если (b, c) ∈ R3 , тогда b – c = 5 ⋅ m для некоторого
целого m.
Суммирование левых и правых частей:
или
для целого числа k + m. ⇒ (a, c) ∈ R3.
Слайд 39
Отношение эквивалентности
разбивает его на подмножества, элементы
которых эквивалентны друг другу
и не эквивалентны элементам других множеств.
В контексте отношений эквивалентности эти
подмножества называются классом
эквивалентности по отношению R.
Слайд 40Пример
Пусть множество А – набор разноцветных шаров, а отношение R задается
(a, b) ∈ R тогда и только тогда, когда a и b имеют одинаковый цвет. Поскольку R – отношение эквивалентности, каждый класс эквивалентности будет состоять из шаров, имеющих одинаковый цвет.
Если определить отношение R условием:
(a, b) ∈ R тогда и только тогда, когда шары a и b имеют одинаковый диаметр, то каждый класс эквивалентности будет состоять из шаров одинакового размерами.
Слайд 41Определение
Пусть a ∈ A, и R - отношение эквивалентности на А
{x: xRa} = {x: (x, a) ∈ R}, называемое классом эквивалентности, содержащим а.
Символ [A]R обозначает множество всех классов эквивалентности множества А по отношению R.
Слайд 42Пример
Отношение R1 есть отношение эквивалентности на множестве А = {1, 2,
Классы эквивалентности по отношению R1 были получены путем определения класса эквивалентности каждого элемента множества А:
где 1 ∈[1], поскольку (1, 1) ∈ R1,
2 ∈[1], поскольку (2, 1) ∈ R1,
4 ∈[1], поскольку (4, 1) ∈ R1, и не существует иного х из А, что (х, 1) ∈ R1. Также:
Слайд 45
Из примера видно, что любой элемент класса эквивалентности порождает класс эквивалентности.
Если b ∈ [a], то [a] = [b].
Любой класс эквивалентности представляет класс.
Каждый класс эквивалентности содержит по крайней мере один элемент.
В силу рефлексивности отношения, множество всех элементов, эквивалентных элементу а, должно содержать а.
С другой стороны, никакой элемент не может принадлежать двум различным классом эквивалентности.
Слайд 46Пример
Рассмотрим отношение эквивалентности R3 и примера (**). Для множества А всех
Поскольку
следует
Слайд 48
представляют собой различные классы эквивалентности по отношению R3 .
Таким образом
Элементы [0] “похожи” в том смысле, что каждый из них кратен пяти.
Элементы другого класса эквивалентности “похожи” том смысле, что имеют один и тот же остаток при делении на пять.
Слайд 49Определения
Совокупность классов эквивалентности разделяет все множество А на непустые взаимоисключающие, или
Такое разделение множества называется его разбиением.
Пусть A и I – множества и пусть 〈А〉 = {Ai : i ∈ I}, где I непусто, есть множество непустых подмножеств множества А. Множество 〈А〉 называется разбиением А, если выполнены условия:
Слайд 50Теорема
Непустое множество подмножеств 〈А〉 множества А есть разбиение А тогда и
Слайд 51Пример
Пусть
Рассмотрим разбиение
Необходимо определить R таким образом:
R
Итак
есть отношение, соответствующее данному разбиению.









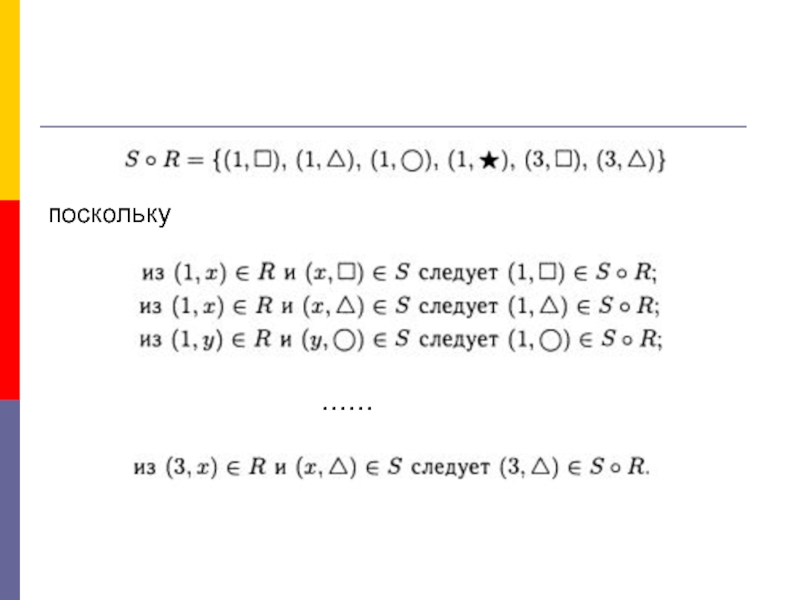























![ОпределениеПусть a ∈ A, и R - отношение эквивалентности на А × А. Пусть [а]](/img/tmb/4/385858/9b3b913fce7426ae3983d9f675152289-800x.jpg)



![Из примера видно, что любой элемент класса эквивалентности порождает класс эквивалентности. Если b ∈ [a],](/img/tmb/4/385858/7f1eabc1b1b9f8ca0bb36545935002f1-800x.jpg)


![представляют собой различные классы эквивалентности по отношению R3 . Таким образом Элементы [0]](/img/tmb/4/385858/a17c425c560f3b3309a68e8f1917a371-800x.jpg)









