- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Анализ временных рядов. Модели и прогнозирование презентация
Содержание
- 1. Анализ временных рядов. Модели и прогнозирование
- 2. ИСХОДНЫЕ СТАТИСТИЧЕСКИЕ ДАННЫЕ
- 3. ИСХОДНЫЕ СТАТИСТИЧЕСКИЕ ДАННЫЕ Говоря о проблеме прогнозирования
- 4. ОСНОВНЫЕ ФАКТОРЫ ВРЕМЕННЫХ РЯДОВ Долговременные, формирующие общую
- 5. ОБЩИЕ МОДЕЛИ ВРЕМЕННЫХ РЯДОВ
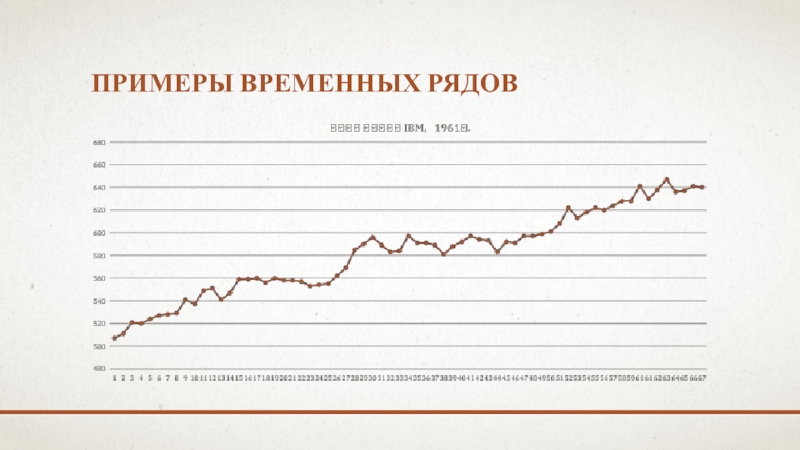
- 6. ПРИМЕРЫ ВРЕМЕННЫХ РЯДОВ
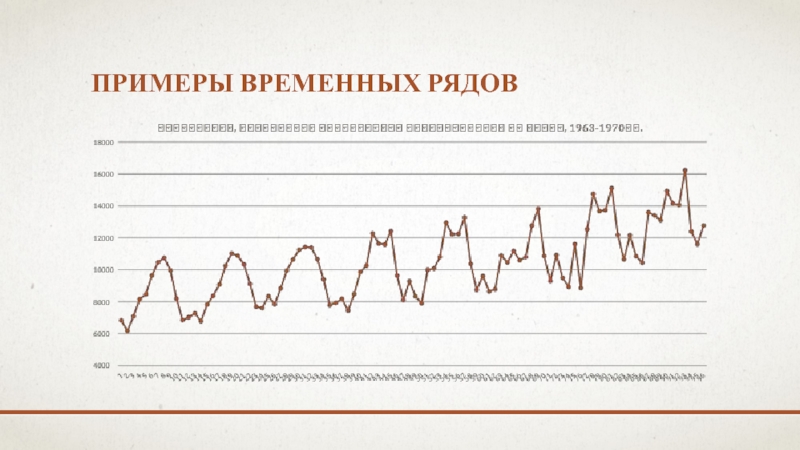
- 7. ПРИМЕРЫ ВРЕМЕННЫХ РЯДОВ
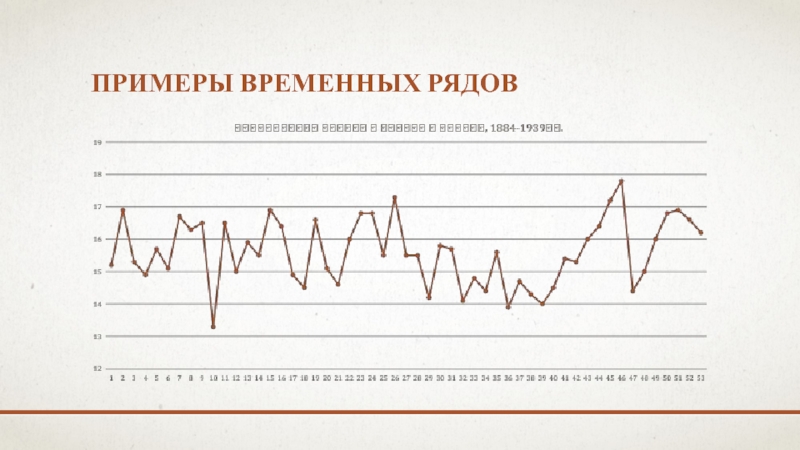
- 8. ПРИМЕРЫ ВРЕМЕННЫХ РЯДОВ
- 9. ЗАДАЧИ АНАЛИЗА ВРЕМЕННЫХ РЯДОВ
- 10. ТЕСТИРОВАНИЕ НАЛИЧИЯ/ОТСУТСТВИЯ НЕСЛУЧАЙНОЙ СОСТАВЛЯЮЩЕЙ
- 11. КРИТЕРИЙ СЕРИЙ, ОСНОВАННЫЙ НА МЕДИАНЕ
- 12. КРИТЕРИЙ «ВОСХОДЯЩИХ» И «НИСХОДЯЩИХ» СЕРИЙ
- 13. КРИТЕРИЙ АББЕ
- 14. МЕТОДЫ СГЛАЖИВАНИЯ ВРЕМЕННОГО РЯДА
- 15. АНАЛИТИЧЕСКИЕ МЕТОДЫ ОЦЕНКИ НЕСЛУЧАЙНОЙ СОСТАВЛЯЮЩЕЙ
- 16. АНАЛИТИЧЕСКИЕ МЕТОДЫ ОЦЕНКИ НЕСЛУЧАЙНОЙ СОСТАВЛЯЮЩЕЙ На практике
- 17. АНАЛИТИЧЕСКИЕ МЕТОДЫ ОЦЕНКИ НЕСЛУЧАЙНОЙ СОСТАВЛЯЮЩЕЙ Для каждого
- 18. АНАЛИТИЧЕСКИЕ МЕТОДЫ ОЦЕНКИ НЕСЛУЧАЙНОЙ СОСТАВЛЯЮЩЕЙ II тип
- 19. АНАЛИТИЧЕСКИЕ МЕТОДЫ ОЦЕНКИ НЕСЛУЧАЙНОЙ СОСТАВЛЯЮЩЕЙ III тип
- 20. АНАЛИТИЧЕСКИЕ МЕТОДЫ ОЦЕНКИ НЕСЛУЧАЙНОЙ СОСТАВЛЯЮЩЕЙ
- 21. КОНЕЦ ЛЕКЦИИ
Слайд 3ИСХОДНЫЕ СТАТИСТИЧЕСКИЕ ДАННЫЕ
Говоря о проблеме прогнозирования на основе одномерных временных рядов,
обычно имеется ввиду кратко- и среднесрочный прогноз, поскольку построение долгосрочного прогноза подразумевает обязательное использование методов организации и статистического анализа специальных экспертных оценок.
Использование доступных к моменту t=N наблюдений временного ряда x(t) для прогнозирования может явиться основой для:
планирования в экономике, производстве, торговле
управления и оптимизации социально-экономических процессов
принятия оптимальных решений в бизнесе
частичного управления параметрами демографических процессов
Использование доступных к моменту t=N наблюдений временного ряда x(t) для прогнозирования может явиться основой для:
планирования в экономике, производстве, торговле
управления и оптимизации социально-экономических процессов
принятия оптимальных решений в бизнесе
частичного управления параметрами демографических процессов
Слайд 4ОСНОВНЫЕ ФАКТОРЫ ВРЕМЕННЫХ РЯДОВ
Долговременные, формирующие общую тенденцию в изменении анализируемого признака
x(t). Обычно описывается при помощи монотонной функции f(t), называемой трендом.
Сезонные, формирующие периодически повторяющиеся в определенное время года колебания анализируемого признака. Описывается периодической функцией ϕ(t) с периодом, кратным сезонам.
Циклические, формирующие изменения анализируемого признака, обусловленные действием долговременных циклов экономической, демографической или астрономической природы. Описывается функцией ?(t).
Случайные, не поддающиеся учету и регистрации. Их воздействие обуславливает стохастическую природу анализируемого признака. Обозначается (t)
Сезонные, формирующие периодически повторяющиеся в определенное время года колебания анализируемого признака. Описывается периодической функцией ϕ(t) с периодом, кратным сезонам.
Циклические, формирующие изменения анализируемого признака, обусловленные действием долговременных циклов экономической, демографической или астрономической природы. Описывается функцией ?(t).
Случайные, не поддающиеся учету и регистрации. Их воздействие обуславливает стохастическую природу анализируемого признака. Обозначается (t)
Слайд 16АНАЛИТИЧЕСКИЕ МЕТОДЫ ОЦЕНКИ НЕСЛУЧАЙНОЙ СОСТАВЛЯЮЩЕЙ
На практике различают четыре основных типа экономического
роста:
I – постоянный рост (с постоянным или близким к нему абсолютным цепным приростом);
II – увеличивающийся рост (с увеличивающимся абсолютным цепным приростом);
III – уменьшающийся рост (с уменьшающимся абсолютным цепным приростом);
IV – рост с качественными изменениями динамических характеристик на протяжении исследуемого периода.
I – постоянный рост (с постоянным или близким к нему абсолютным цепным приростом);
II – увеличивающийся рост (с увеличивающимся абсолютным цепным приростом);
III – уменьшающийся рост (с уменьшающимся абсолютным цепным приростом);
IV – рост с качественными изменениями динамических характеристик на протяжении исследуемого периода.
Слайд 17АНАЛИТИЧЕСКИЕ МЕТОДЫ ОЦЕНКИ НЕСЛУЧАЙНОЙ СОСТАВЛЯЮЩЕЙ
Для каждого типа роста наиболее часто в
практике экономических исследований встречаются следующие виды функций трендов.
I тип роста
Линейная функция: f(t)= α0 + α1 t.
Линейно-гиперболическая функция: f(t)= α + β t + γ / t, где β >0; γ >0.
Линейно-логарифмическая функция 2-го порядка:
f(t)= α0 + α1ln(t) + α2ln2(t), где α1 >0; α2 >0.
I тип роста
Линейная функция: f(t)= α0 + α1 t.
Линейно-гиперболическая функция: f(t)= α + β t + γ / t, где β >0; γ >0.
Линейно-логарифмическая функция 2-го порядка:
f(t)= α0 + α1ln(t) + α2ln2(t), где α1 >0; α2 >0.
Слайд 18АНАЛИТИЧЕСКИЕ МЕТОДЫ ОЦЕНКИ НЕСЛУЧАЙНОЙ СОСТАВЛЯЮЩЕЙ
II тип роста
Показательная функция: f(t)=
α(1+β)t, где α > 0; β > 0.
Парабола 2-го порядка: f(t)= α0 + α1t + α2t2, где α1>0; α2>0.
Парабола 3-го порядка: f(t)= α0 + α1 t + α2 t2 + α3 t3,
где α1>0; α2>0; α3>0.
Парабола 2-го порядка: f(t)= α0 + α1t + α2t2, где α1>0; α2>0.
Парабола 3-го порядка: f(t)= α0 + α1 t + α2 t2 + α3 t3,
где α1>0; α2>0; α3>0.
Слайд 19АНАЛИТИЧЕСКИЕ МЕТОДЫ ОЦЕНКИ НЕСЛУЧАЙНОЙ СОСТАВЛЯЮЩЕЙ
III тип роста
Степенная функция: f(t)= α t β,
где α>0; 0<β<1.
Линейно-логарифмическая функция: f(t)= α0 + α1ln(t), где α1>0.
Парабола 2-го порядка: f(t)= α0 + α1t + α2 t 2, где α1>0; α2>0.
Гипербола 1-го порядка: f(t)= α0 + α1/t, где α1<0.
Гипербола 2-го порядка: f(t)= α0 + α1/t + α2/ t2 , где α1<0; α2<0.
Модифицированная экспонента: f(t)=α + βe-t, где β <0.
Линейно-логарифмическая функция: f(t)= α0 + α1ln(t), где α1>0.
Парабола 2-го порядка: f(t)= α0 + α1t + α2 t 2, где α1>0; α2>0.
Гипербола 1-го порядка: f(t)= α0 + α1/t, где α1<0.
Гипербола 2-го порядка: f(t)= α0 + α1/t + α2/ t2 , где α1<0; α2<0.
Модифицированная экспонента: f(t)=α + βe-t, где β <0.