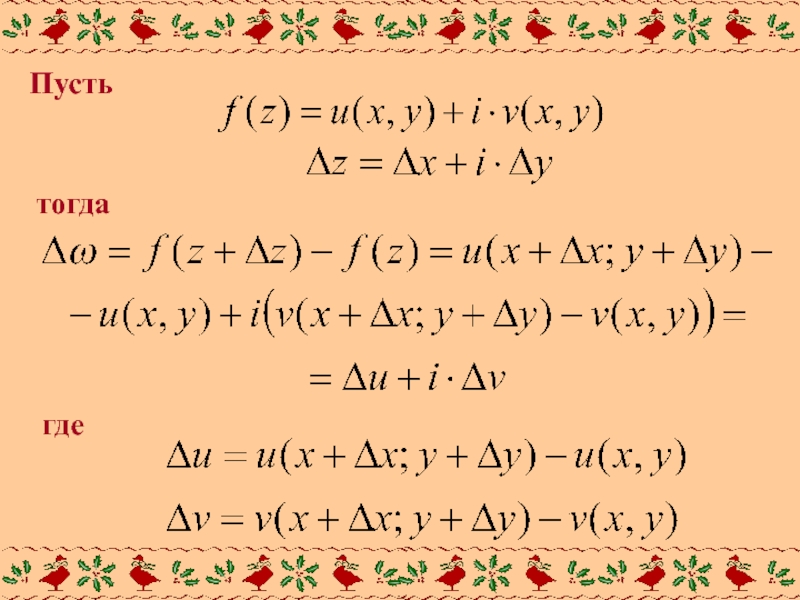- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Аналитические функции презентация
Содержание
- 1. Аналитические функции
- 2. Если существует предел отношения при по
- 3. Требование существования предела отношения и его независимость
- 4. Пусть тогда где
- 5. Тогда Если функция дифференцируема в точке
- 6. Если Δz = iΔy, то есть точка
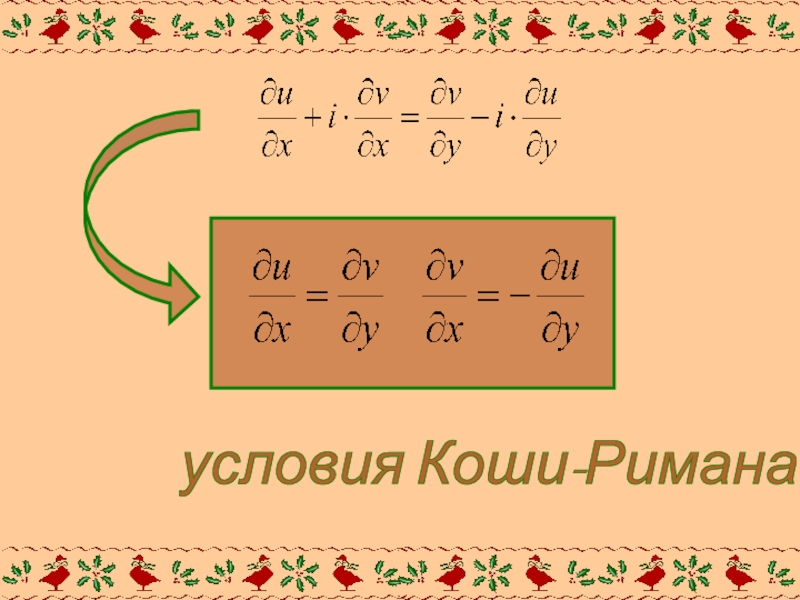
- 7. условия Коши-Римана
- 8. Это необходимое условие дифференцируемости ФКП. Оно должно
- 9. Точки плоскости z, в которых функция f(z)
- 10. ПРИМЕРЫ. 1 Выяснить, являются ли данные функции аналитичными: 2 3
- 11. 1 Условия Коши-Римана выполняются во всех
- 12. 2 Условия Коши-Римана выполняются во всех
- 13. 3 Условия Коши-Римана не выполняются, следовательно
Слайд 122.5. АНАЛИТИЧЕСКИЕ ФУНКЦИИ
Введем понятие производной ФКП.
Пусть независимой переменной
дано приращение
Приращение функции w=f(x):
Слайд 2
Если существует предел отношения
при
по любому закону, то этот
предел называется производной функции
Обозначают:
Слайд 3Требование существования предела отношения
и его независимость от закона стремления к нулю
Для функции действительного аргумента предел существует при приближении точки х+Δх к точке х по двум направлениям (слева и справа).
Для функции комплексного переменного точка z+Δz должна приближаться к точке z по любому пути, и пределы по всем направлениям должны быть одинаковы.
Слайд 5Тогда
Если функция дифференцируема в точке z, то этот предел существует
Если Δz = Δх, то есть точка z+Δz приближается к точке z по прямой, параллельной оси х, то
Слайд 6Если Δz = iΔy, то есть точка z+Δz приближается к точке
Так как
не должен зависеть от закона стремления
то
Слайд 8Это необходимое условие дифференцируемости ФКП. Оно должно выполнятся в любой точке,
Если функция комплексного аргумента
однозначна и дифференцируема не только
в данной точке, но и в некоторой
окрестности этой точки, то она
называется аналитической в данной точке.
Слайд 9Точки плоскости z, в которых функция f(z)
аналитична, называются правильными
точками этой функции.
Точки
неаналитична, называются особыми
точками.
Функция, дифференцируемая во всех точках
некоторой области, называется
аналитической в данной области.