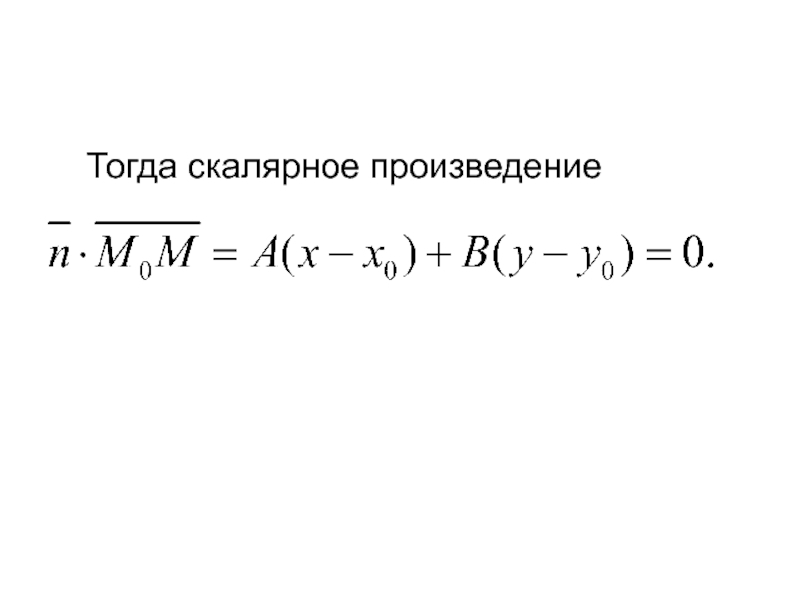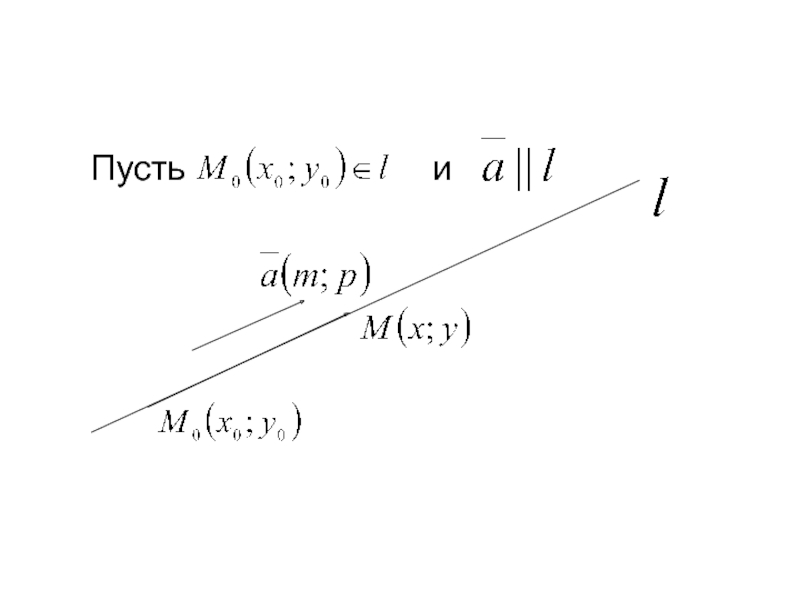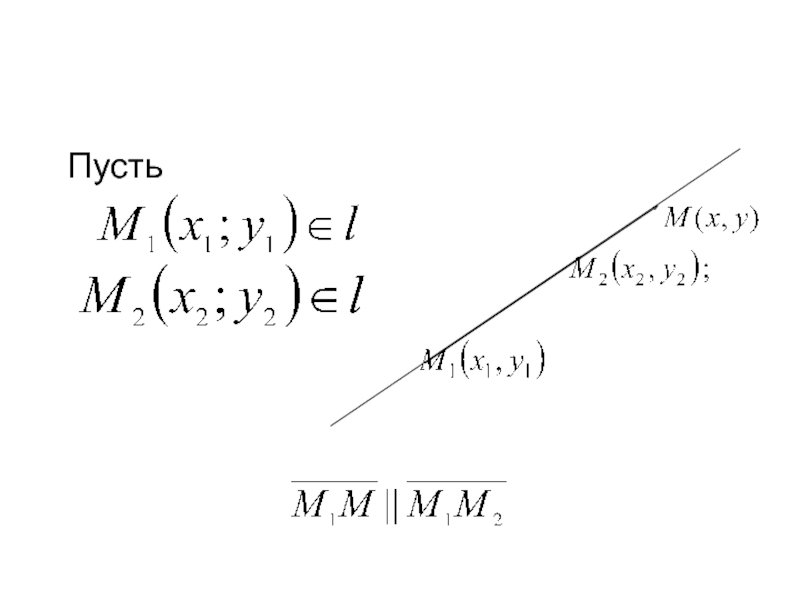- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Аналитическая геометрия. Прямая на плоскости презентация
Содержание
- 1. Аналитическая геометрия. Прямая на плоскости
- 2. Прямая на плоскости
- 3. Определение. Уравнением линии на
- 4. Теорема. Всякое
- 5. Уравнение прямой, проходящей через точку перпендикулярно вектору
- 6. Введем следующие понятия. Вектор,
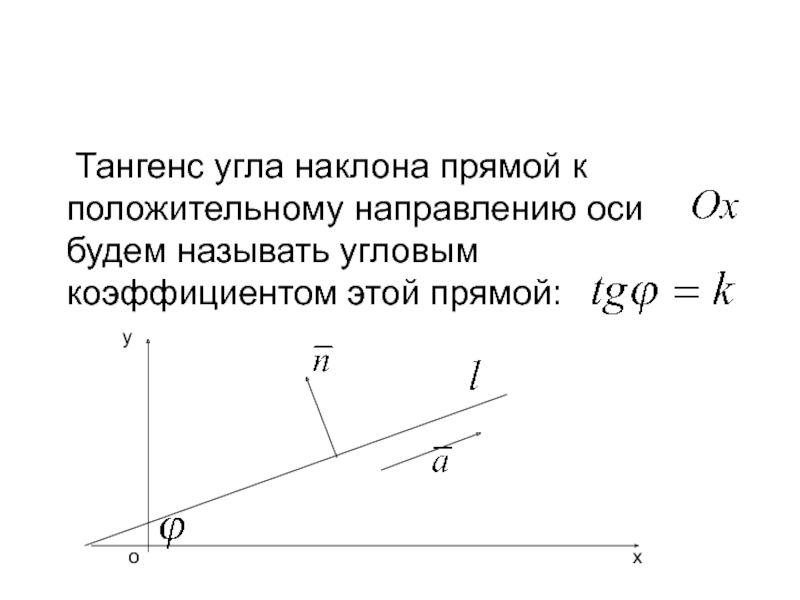
- 7. Тангенс угла наклона прямой
- 8. Пусть точка
- 9. Тогда скалярное произведение
- 10. Получили уравнение прямой, проходящей через заданную точку, перпендикулярно данному вектору:
- 11. Общее уравнение прямой Из
- 12. Каноническое уравнение прямой
- 14. Тогда из условия
- 15. Пример Написать уравнения прямых, проходящих
- 16. Уравнение прямой, проходящей через две точки
- 17. Пусть
- 18. Координаты этих векторов пропорциональны:
- 19. Параметрические уравнения прямой Приравняем
- 20. Уравнение прямой с угловым коэффициентом
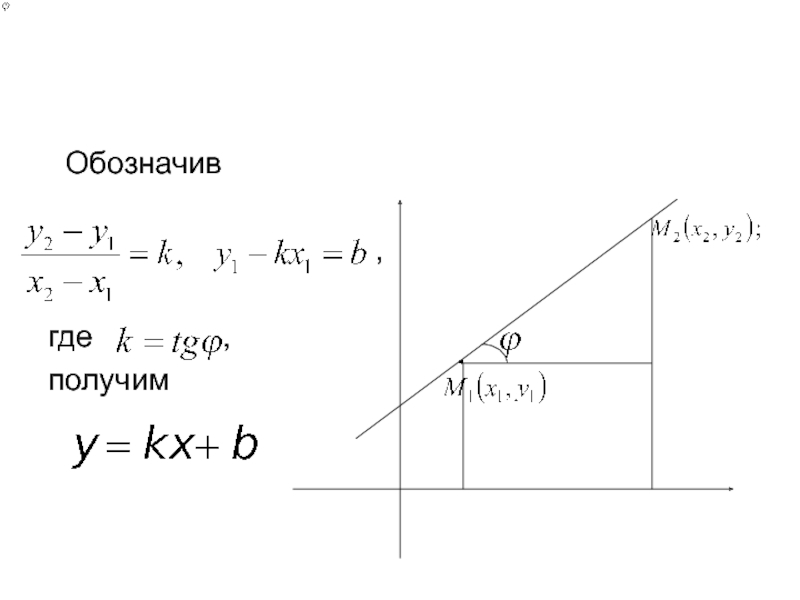
- 21. Обозначив
- 22. Уравнение прямой ,проходящей через точку
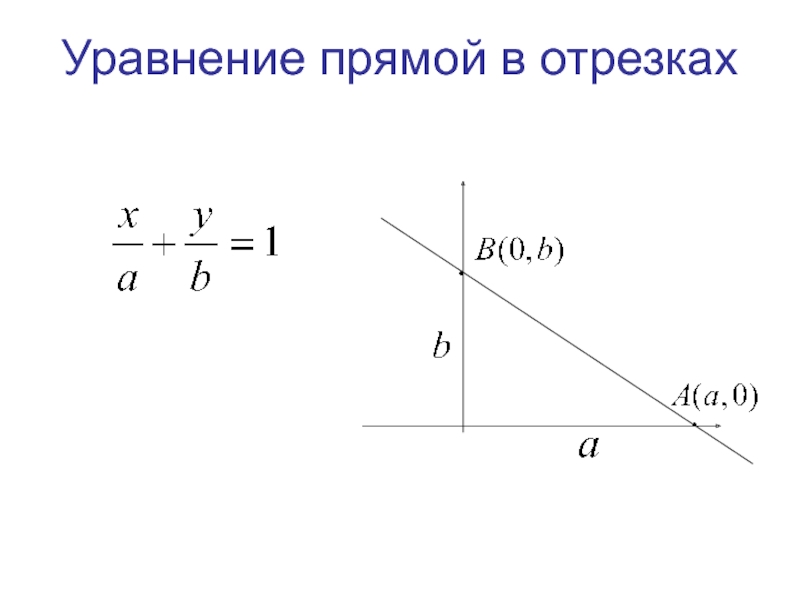
- 23. Уравнение прямой в отрезках
- 24. Взаимное расположение прямых
- 25. Угол между двумя прямыми Пусть две прямые заданы общими уравнениями
- 26. Тогда угол между этими
- 27. Пусть даны прямые
- 28. Тогда
- 29. Условия параллельности Прямые
- 30. Условие перпендикулярности
- 31. Расстояние от точки до прямой
- 32. Пример Найти уравнение прямой,
Слайд 3
Определение. Уравнением линии на плоскости
называется уравнение, которому удовлетворяют координаты и любой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.
Слайд 4
Теорема. Всякое уравнение первой степени
где А и В не обращаются в нуль одновременно, представляет собой уравнение некоторой прямой линии на плоскости
Слайд 6
Введем следующие понятия. Вектор, перпендикулярный прямой
будем называть нормалью прямой и обозначать Итак, .
Вектор, параллельный прямой, будем называть направляющим вектором этой прямой. Обозначим его
Вектор, параллельный прямой, будем называть направляющим вектором этой прямой. Обозначим его
Слайд 7
Тангенс угла наклона прямой к положительному направлению оси будем
называть угловым коэффициентом этой прямой:
о
х
у
Слайд 10
Получили уравнение прямой, проходящей через заданную точку, перпендикулярно
данному вектору:
Слайд 14
Тогда из условия коллинеарности векторов
и получаем каноническое, т. е. простейшее уравнение прямой:
Слайд 15Пример
Написать уравнения прямых, проходящих через точку
параллельно
и перпендикулярно вектору .
Первое уравнение и
второе .
Первое уравнение и
второе .
Слайд 18
Координаты этих векторов пропорциональны:
Получили уравнение прямой, проходящей через две
точки.
Слайд 19Параметрические уравнения прямой
Приравняем обе части соотношения
к t. Получим
параметрические уравнения прямой
Слайд 22 Уравнение прямой ,проходящей через точку
Пусть точка
лежит на
прямой . Тогда
Вычтем из первого второе соотношение . Получим
прямой . Тогда
Вычтем из первого второе соотношение . Получим
Слайд 29Условия параллельности
Прямые параллельны тогда и только тогда, когда выполняется
одно из двух условий ( в зависимости от вида уравнений прямых).