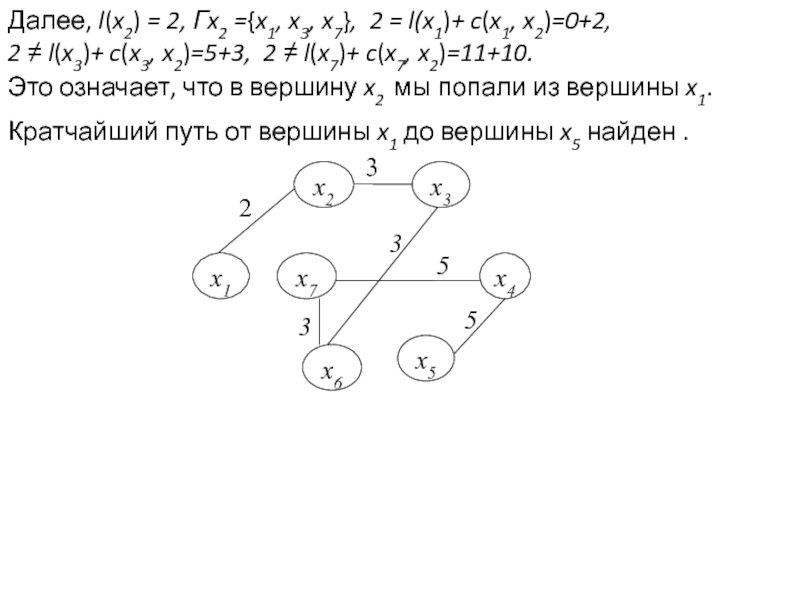
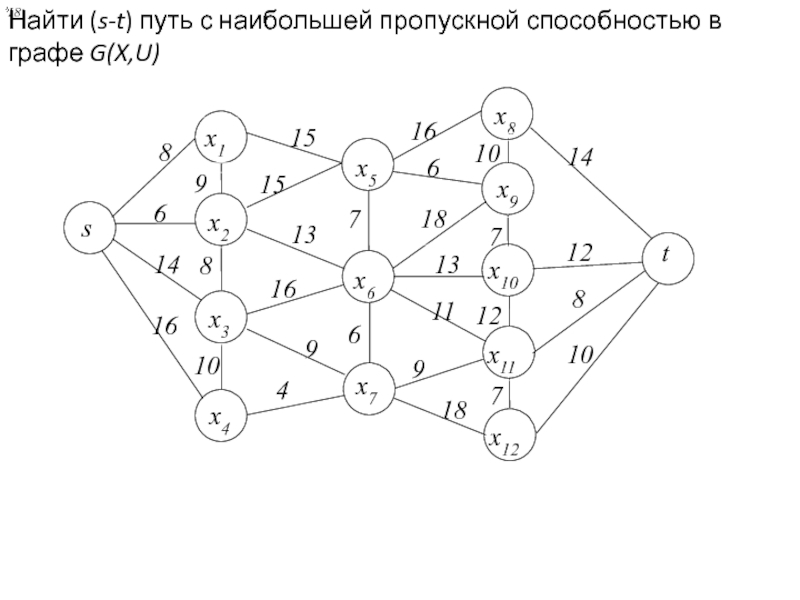
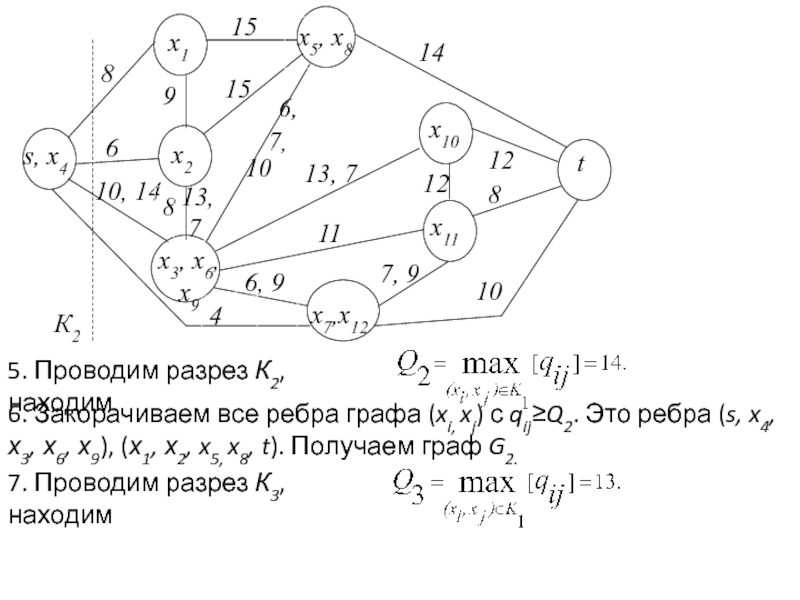
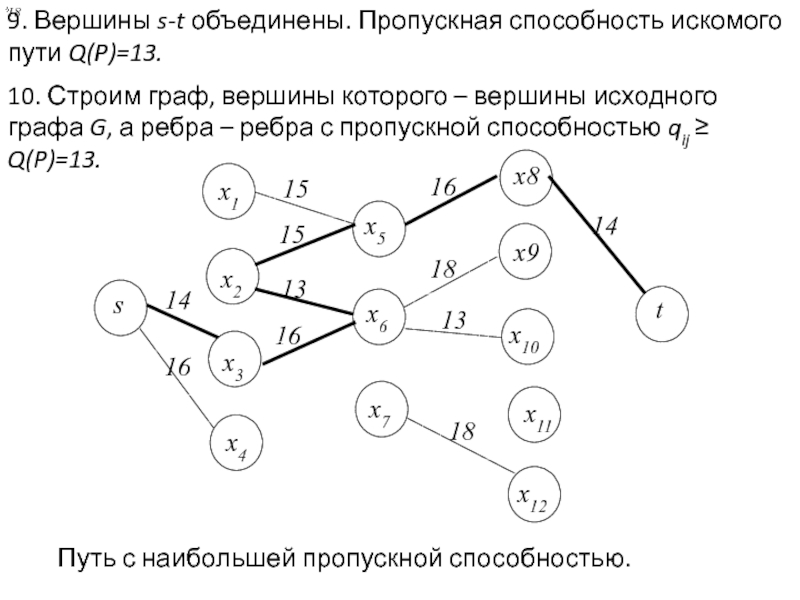
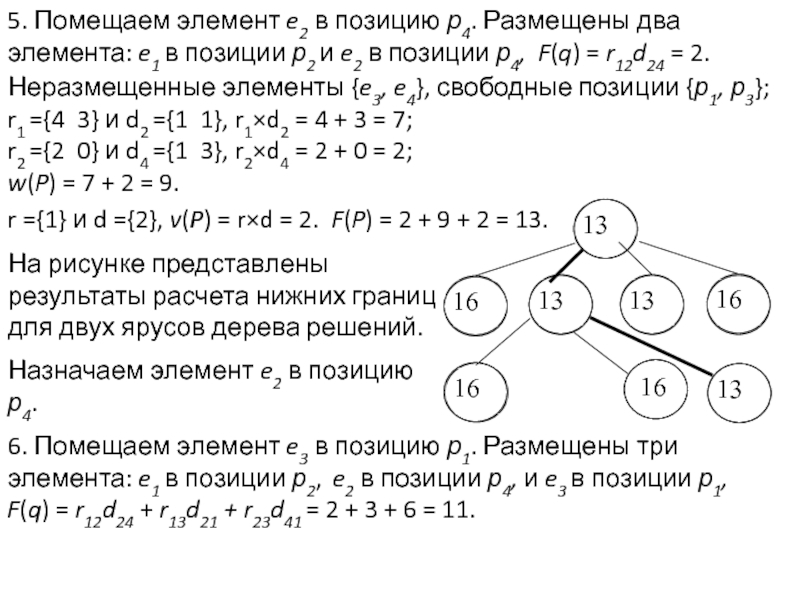
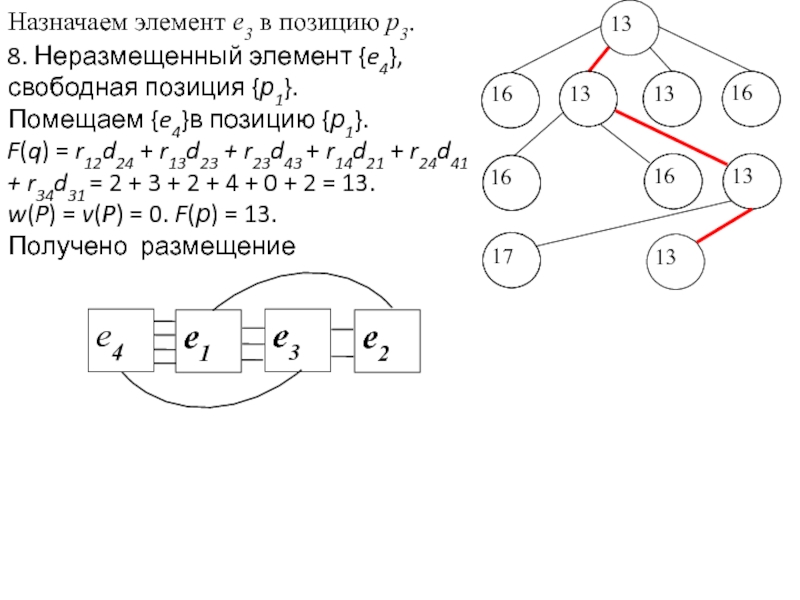
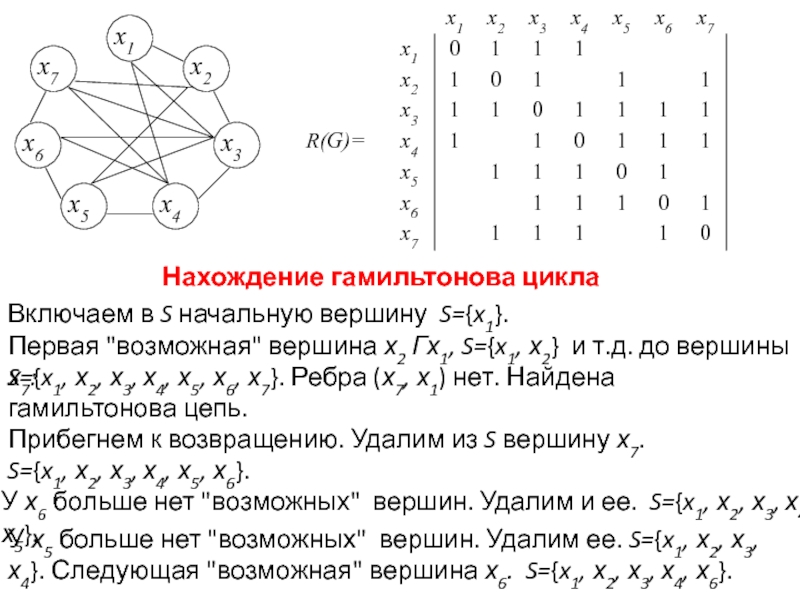
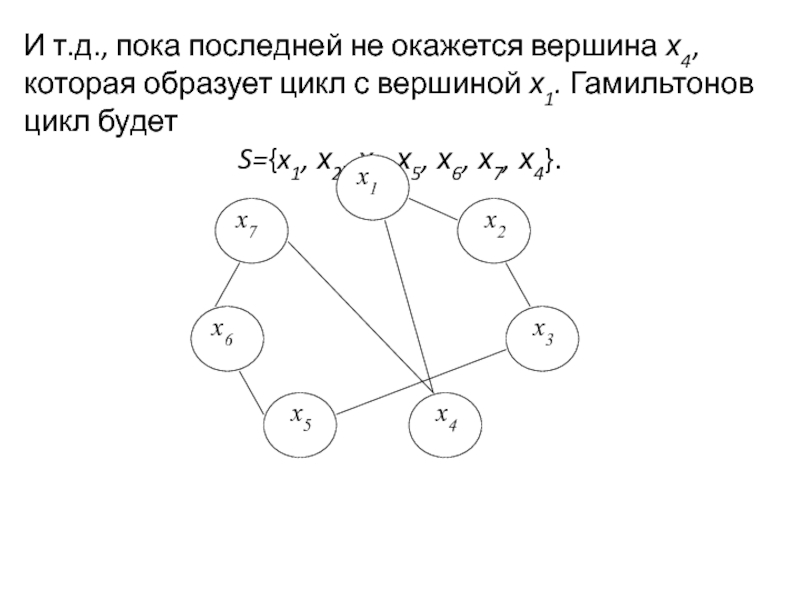
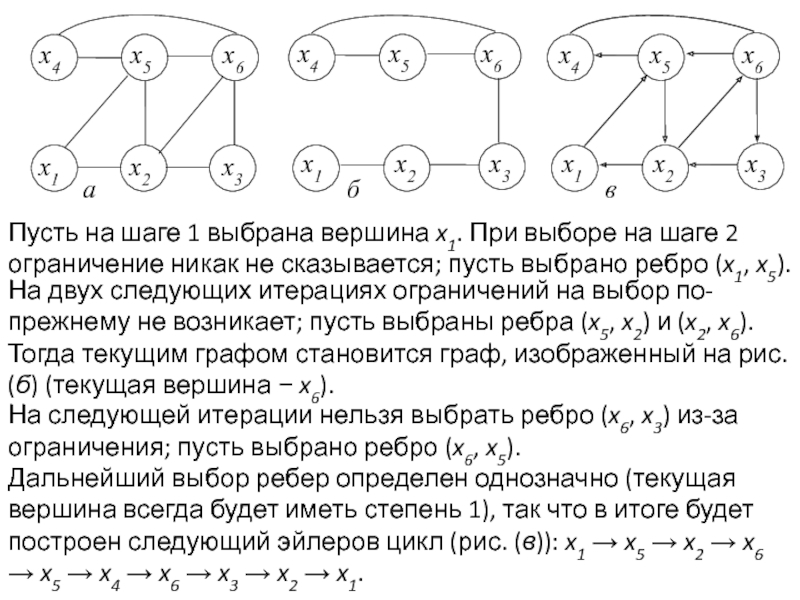
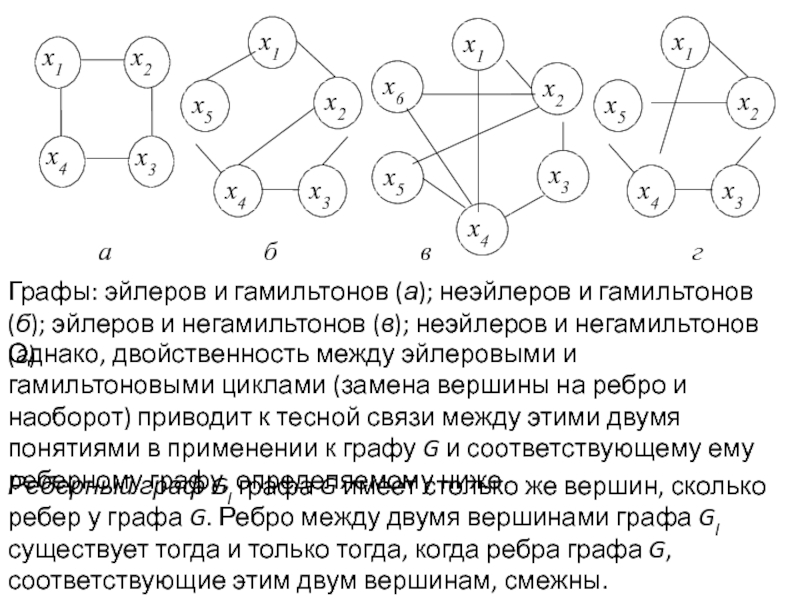
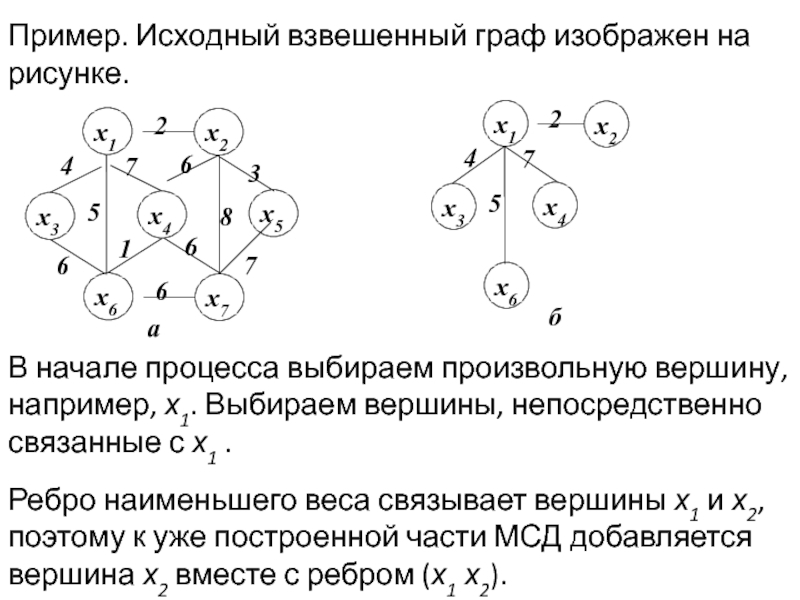
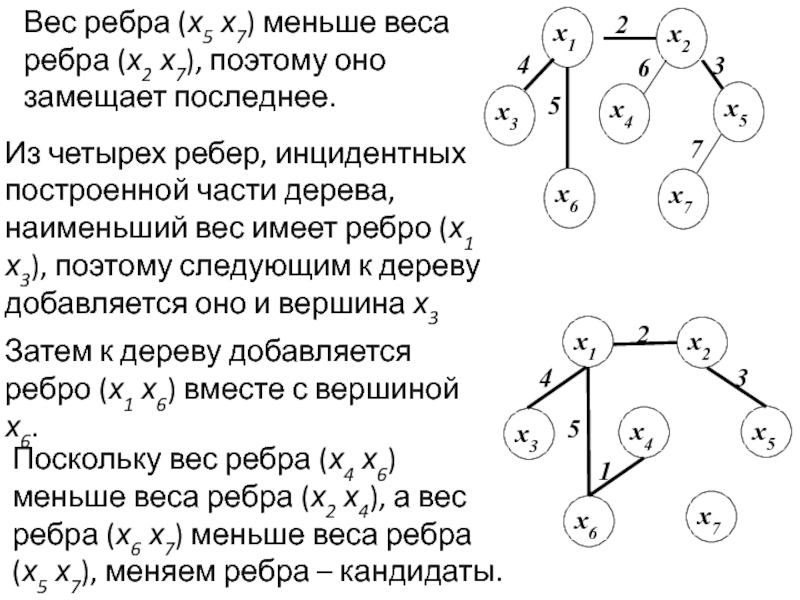
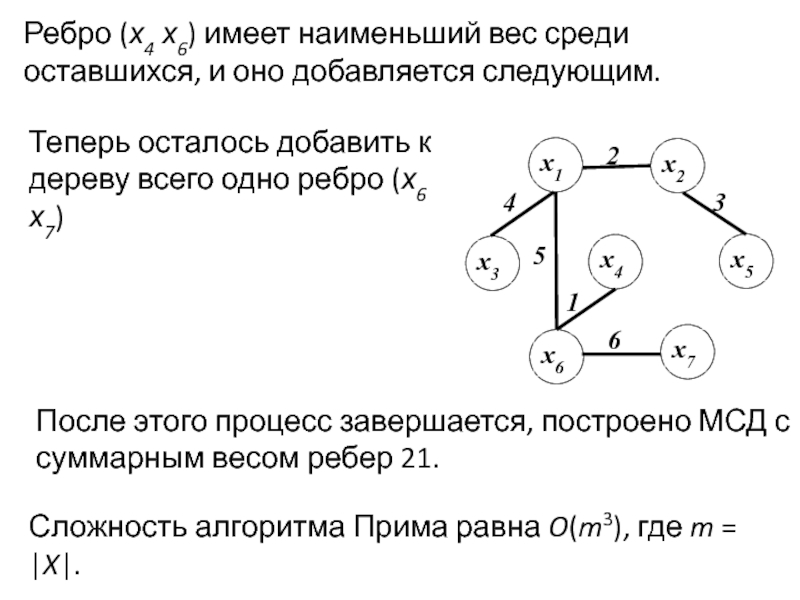
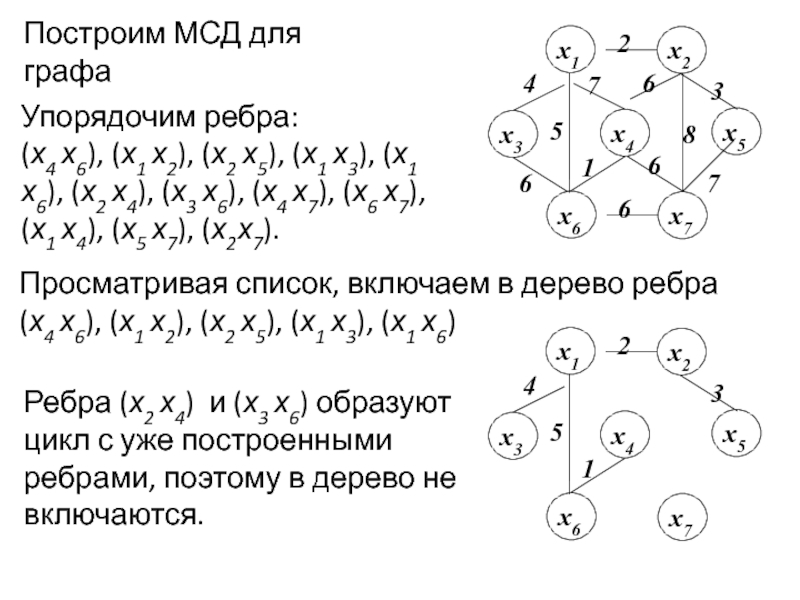
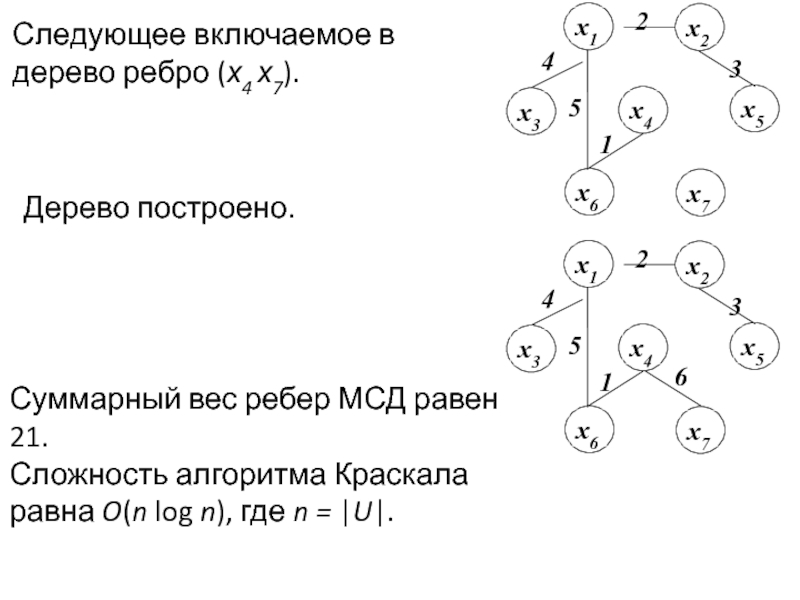
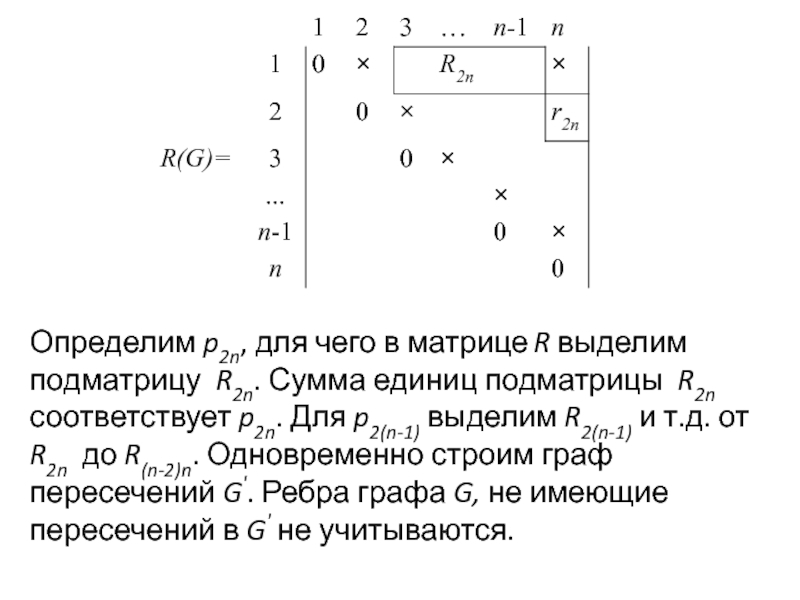
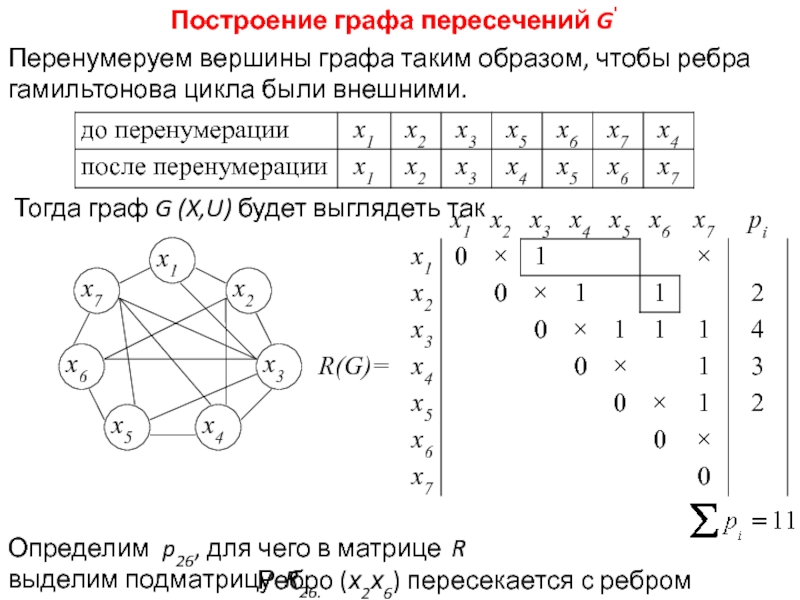
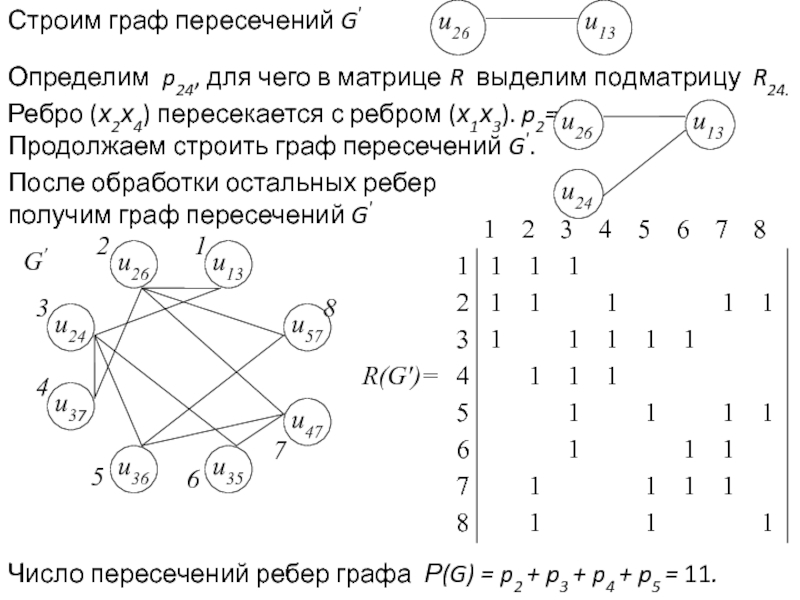
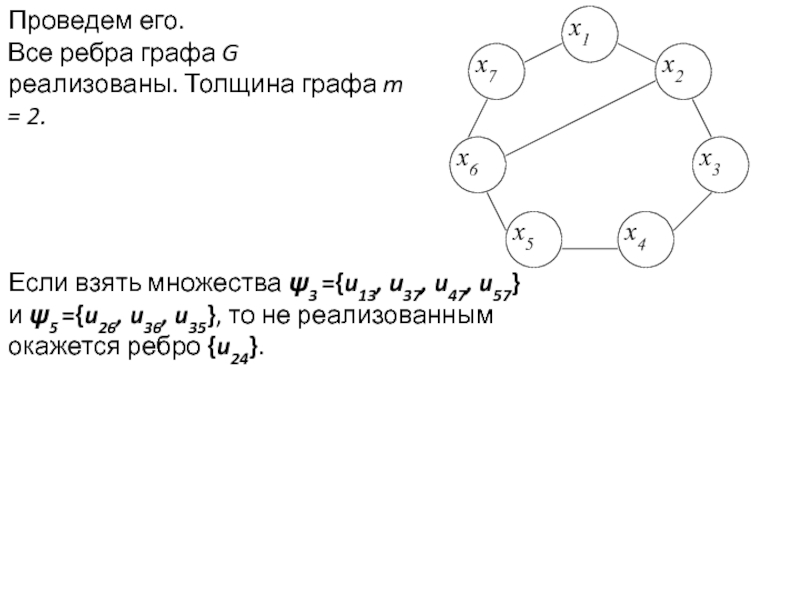
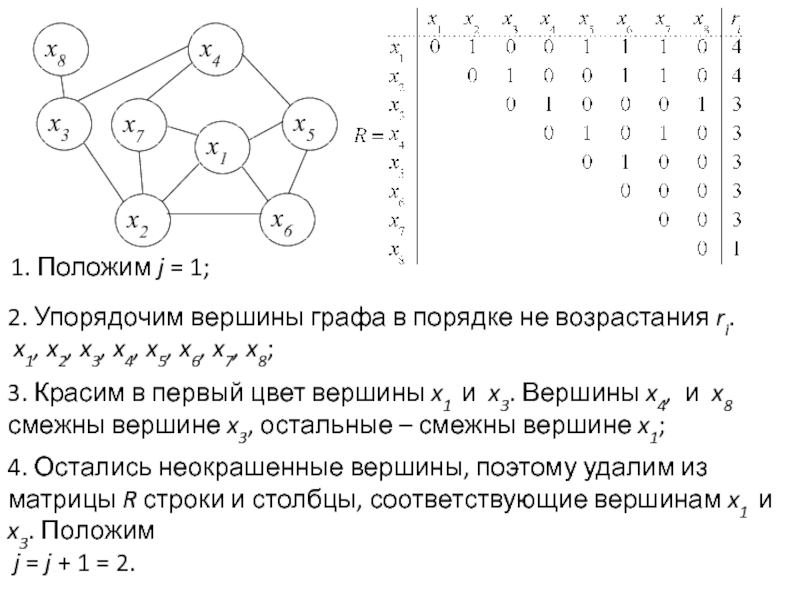
Задача раскраски вершин графа относится к NP-полным задачам. Различают точные и приближенные алгоритмы раскраски.
Примером точных алгоритмов служит алгоритм Вейссмана.
Алгоритм состоит из двух частей:
1. Построение семейства максимальных внутренне устойчивых множеств (МВУМ) (метод Магу);
2. Выбор минимального числа МВУМ, покрывающих все вершины графа (метод Петрика).
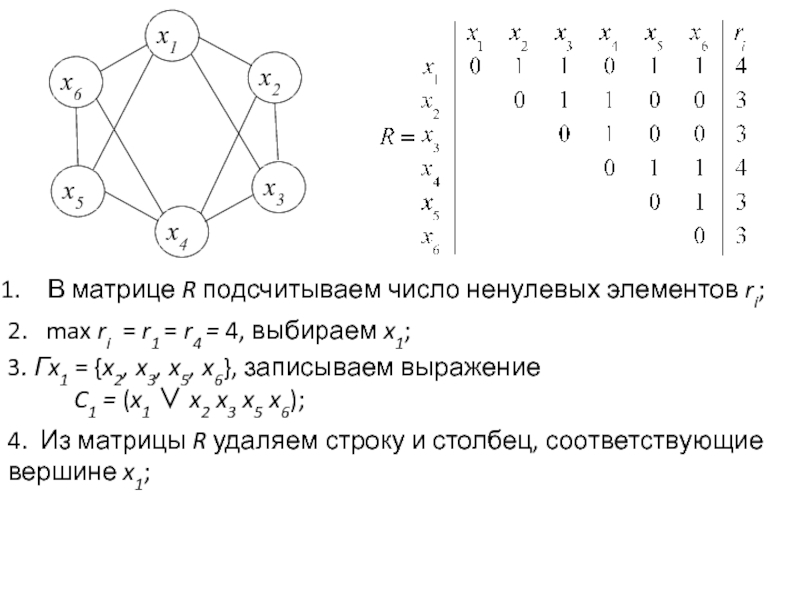
Множество вершин Хs графа G(X,U) называется внутренне устойчи-вым (независимым), если никакие две вершины из этого множества не смежны, Xs⊂X [ГXs∩Xs=∅]. Внутренне устойчивое множество называется максимальным, если оно не является собственным подмножеством некоторого другого независимого множества.











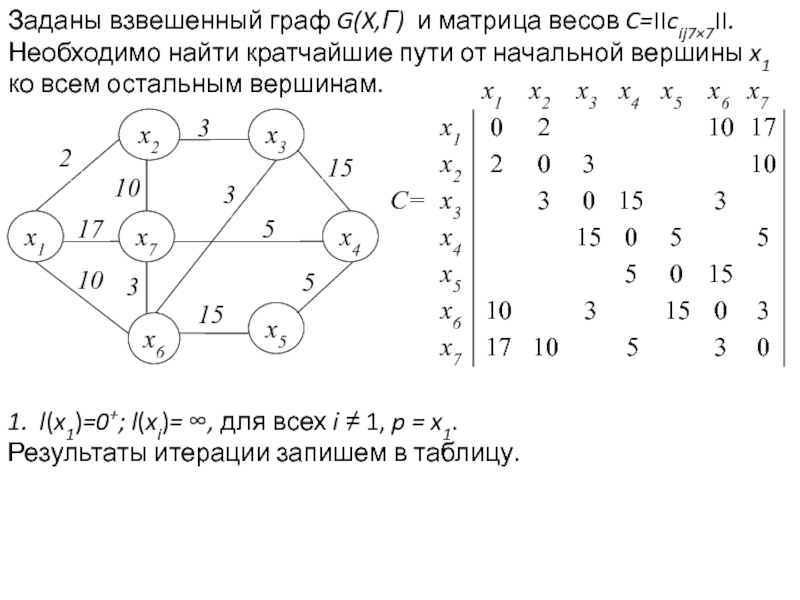
![2. Гp ={x2, x6, x7} – все пометки временные, уточним их: l(x2)=min[∞ ,0++2]=2;](/img/tmb/5/441259/789b546306732480326a5a6ac674a30b-800x.jpg)
![6. l(xi*) = min[l(xi)] = l(x3) = 5.7. l(x3) = 5+, p=x3.8. Не все вершины](/img/tmb/5/441259/c4f756d48f50eee3e26df76b48fa7a2a-800x.jpg)
![12. l(xi*) = min[l(xi)] = l(x7) = 11.13. l(x7) = 11+, p=x7.14. Не все пометки](/img/tmb/5/441259/220cd0e539e5c6a27b729ef8bf398ae9-800x.jpg)