- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Алгебраические фракталы презентация
Содержание
- 1. Алгебраические фракталы
- 2. Динамическая система Динамическая система - математическая абстракция,
- 3. Фазовое пространство Фазовое пространство - пространство, на
- 4. Неподвижные точки, циклы
- 5. Неподвижные точки, циклы
- 6. Аттракторы Аттрактор (англ. attract - привлекать, притягивать)
- 7. Аттракторы Репеллер (англ. repel - отталкивать) -
- 8. Недетерминированный хаос Хаос - неупорядоченное, случайное, непрогнозируемое
- 9. Детерминированный хаос Поведение большинства физических систем описывается
- 10. Детерминированный хаос Невозможность предсказания поведения системы обусловлена
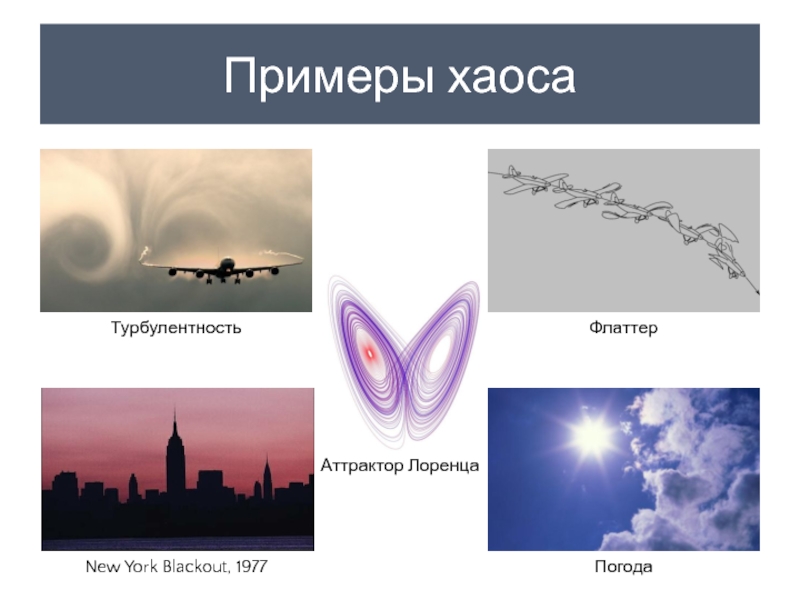
- 11. Примеры хаоса Турбулентность Флаттер New York Blackout, 1977 Аттрактор Лоренца Погода
- 12. Метод Ньютона
- 13. Метод Ньютона для кубического полинома
- 14. Построение
- 15. Бассейны Ньютона
- 16. Замечания
- 17. Динамическая система квадратичного отображения
- 18. Простейший случай
- 19. Множества Жюлиа и Фату
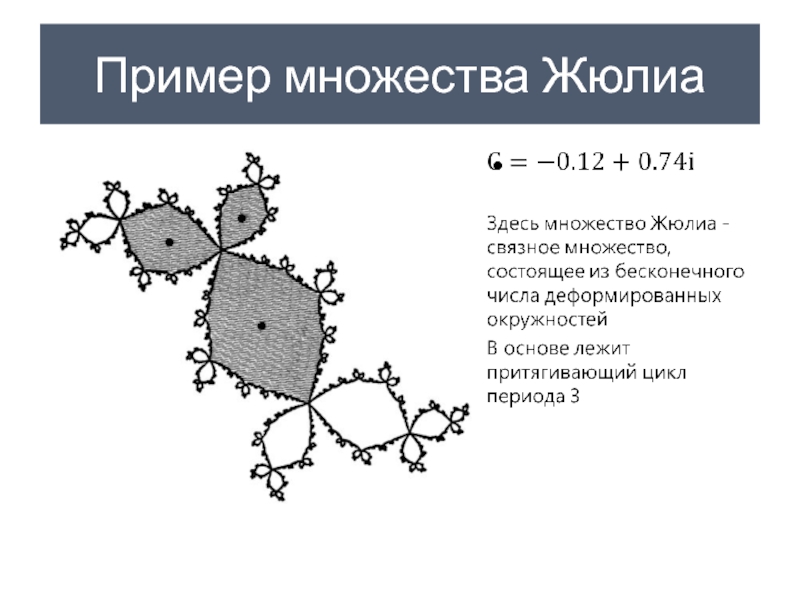
- 20. Пример множества Жюлиа
- 21. Пример пыли Фату
- 22. Замечания
- 23. Определение множества Мандельброта
- 24. Множество Мандельброта
- 25. Альтернативное определение
- 26. Связь определений Точка 0 – единственная критическая
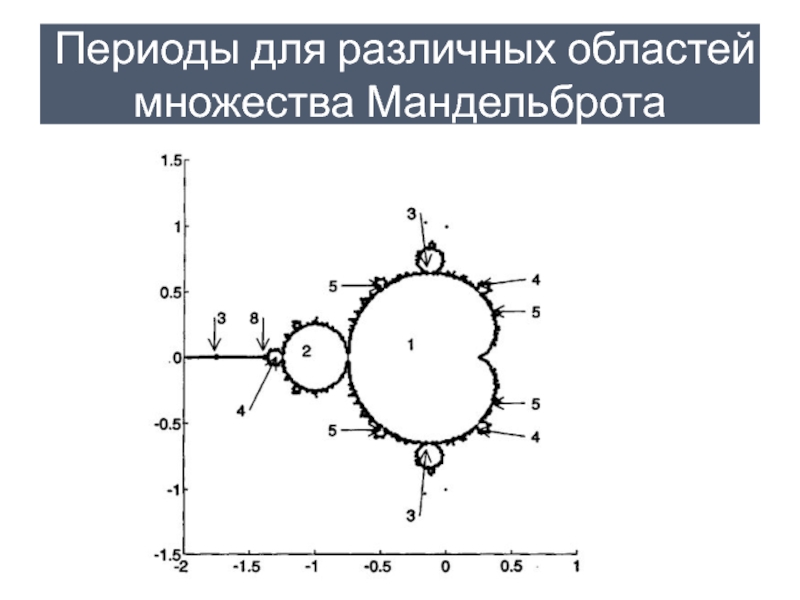
- 27. Периоды для различных областей множества Мандельброта
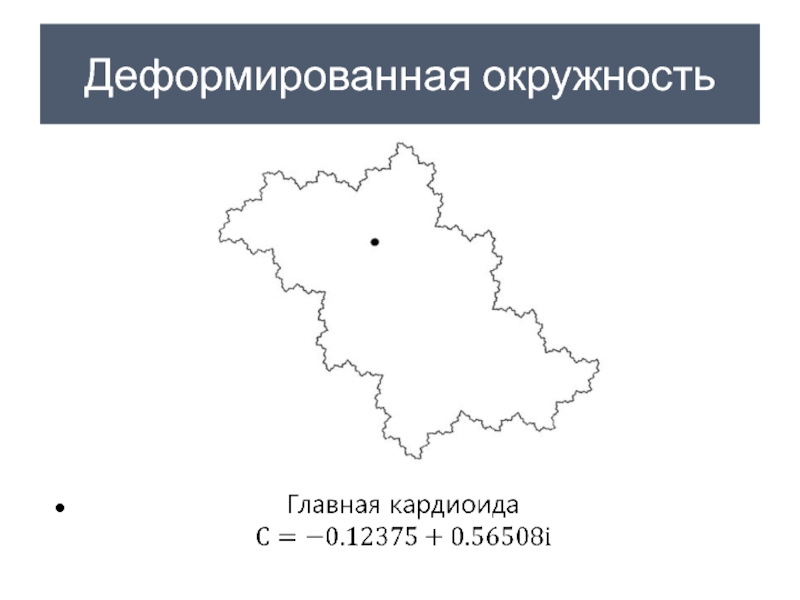
- 28. Деформированная окружность
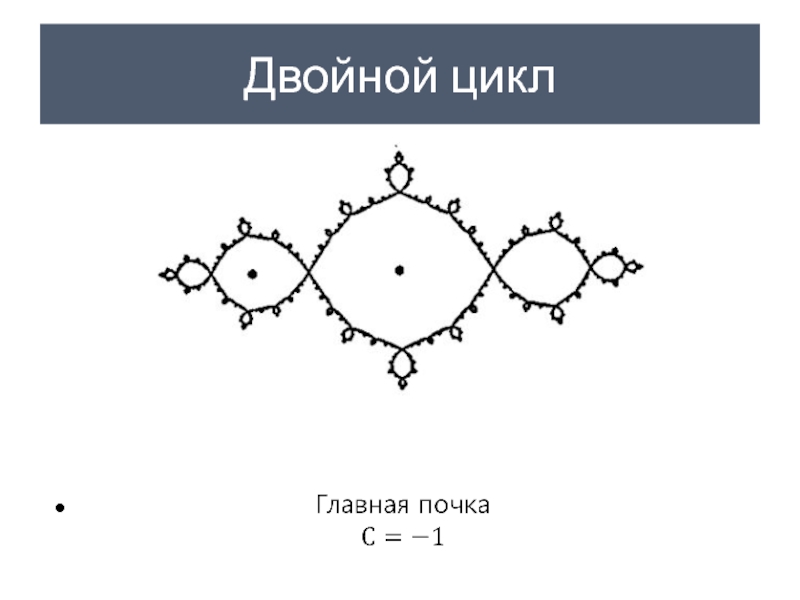
- 29. Двойной цикл
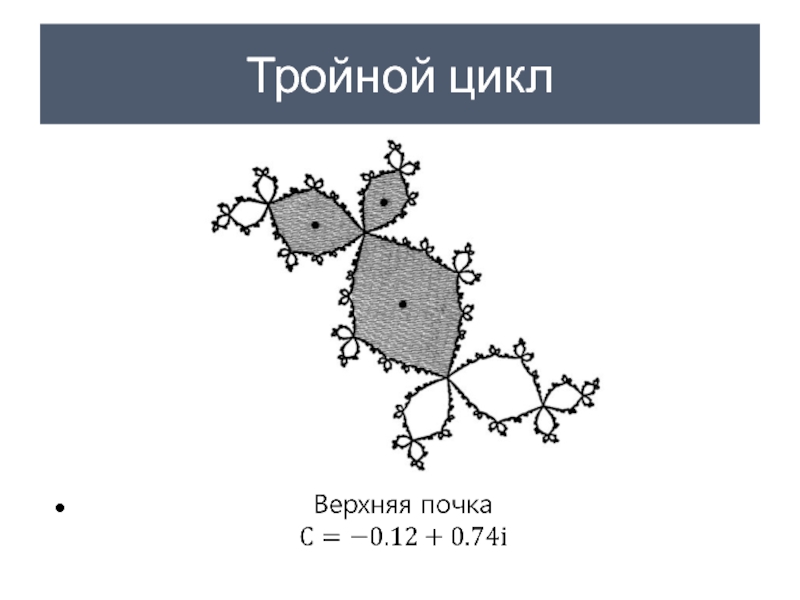
- 30. Тройной цикл
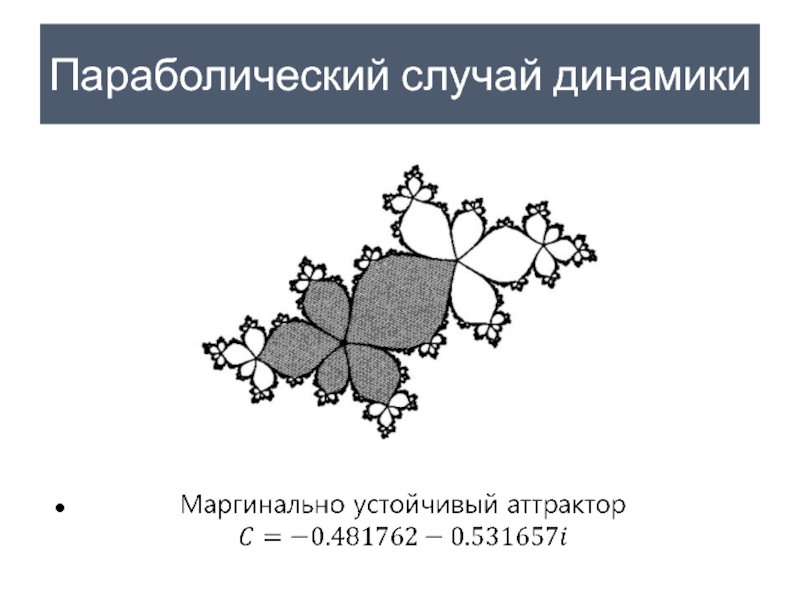
- 31. Параболический случай динамики
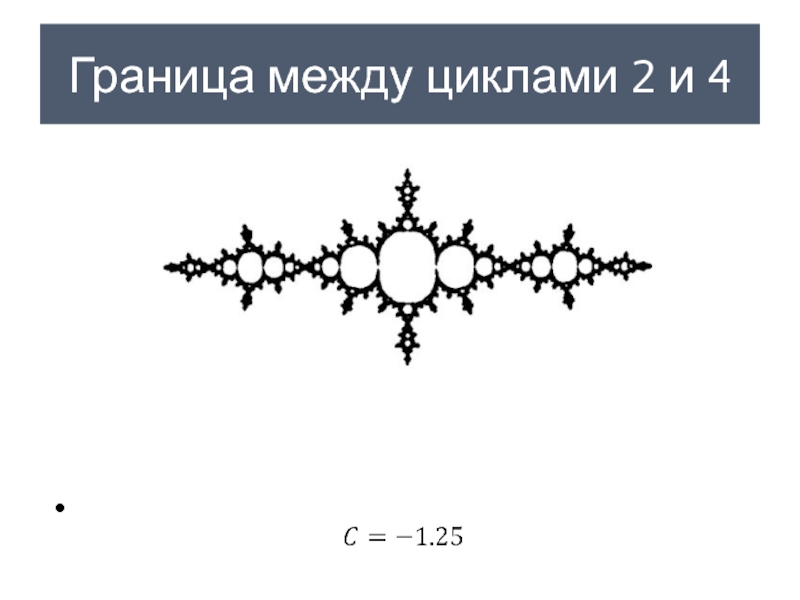
- 32. Граница между циклами 2 и 4
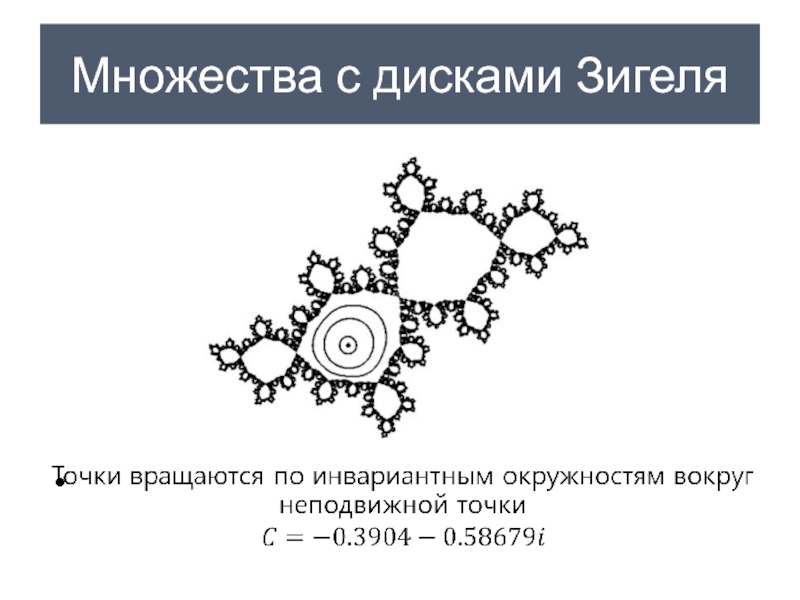
- 33. Множества с дисками Зигеля
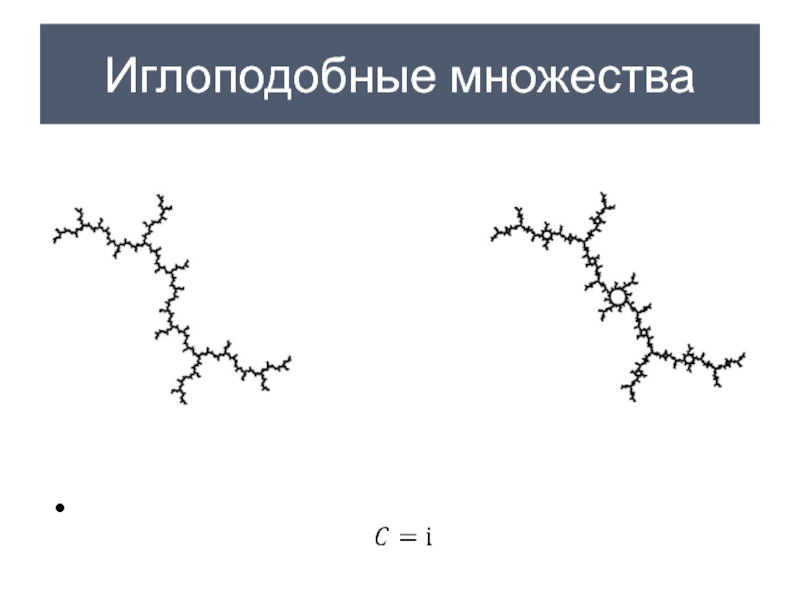
- 34. Иглоподобные множества
- 35. Пыль Фату
- 36. Построение
- 37. Спасибо за внимание
Динамическая система Динамическая система - математическая абстракция, предназначенная для описания и изучения систем, эволюционирующих с течением времени При этом время может быть как вещественным, так и дискретным
Слайд 2Динамическая система
Динамическая система - математическая абстракция, предназначенная для описания и изучения
систем, эволюционирующих с течением времени
При этом время может быть как вещественным, так и дискретным
При этом время может быть как вещественным, так и дискретным
Слайд 3Фазовое пространство
Фазовое пространство - пространство, на котором представлено множество всех состояний
системы для некоторого фиксированного момента времени
Т.е. каждому возможному состоянию системы соответствует точка фазового пространства
Т.е. каждому возможному состоянию системы соответствует точка фазового пространства
Слайд 6Аттракторы
Аттрактор (англ. attract - привлекать, притягивать) — множество состояний (точек фазового
пространства) динамической системы, к которому она стремится с течением времени
Примеры
притягивающая неподвижная точка
периодическая траектория
Примеры
притягивающая неподвижная точка
периодическая траектория
Слайд 7Аттракторы
Репеллер (англ. repel - отталкивать) - множество неустойчивого равновесия динамической системы
В
сложных случаях в динамических системах могут возникать странные аттракторы, т.е. аттракторы с дробной размерностью и хаотической структурой
Множество начальных состояний из которых динамическая система обязательно попадет в аттрактор называется бассейном притяжения аттрактора
Множество начальных состояний из которых динамическая система обязательно попадет в аттрактор называется бассейном притяжения аттрактора
Слайд 8Недетерминированный хаос
Хаос - неупорядоченное, случайное, непрогнозируемое поведение элементов системы
Недетерминированный хаос -
это отражение сложного поведения большого количества частиц
Пример: броуновское движение мелких частиц в воде
Невозможно спрогнозировать траекторию любой частицы, потому что для этого потребуется определить параметры движения всех молекул воды, которых слишком много
Подчиняется статистическим законам
Пример: броуновское движение мелких частиц в воде
Невозможно спрогнозировать траекторию любой частицы, потому что для этого потребуется определить параметры движения всех молекул воды, которых слишком много
Подчиняется статистическим законам
Слайд 9Детерминированный хаос
Поведение большинства физических систем описывается нелинейными законами
Отклик таких систем непропорционален
силе возмущающего воздействия
Существуют физические системы, отклик которых остается сильным на протяжении длительного времени
Такие системы тоже оказываются хаотическими, а их поведение называют детерминированным хаосом
Существуют физические системы, отклик которых остается сильным на протяжении длительного времени
Такие системы тоже оказываются хаотическими, а их поведение называют детерминированным хаосом
Слайд 10Детерминированный хаос
Невозможность предсказания поведения системы обусловлена не количеством частиц, а большим
влиянием небольших погрешностей в определении состояния
Погрешности нельзя исключить, в частности, в соответствии с принципом неопределенности Гейзенберга
Поведение таких детерминированных систем тоже лучше описывается статистическими законами
Погрешности нельзя исключить, в частности, в соответствии с принципом неопределенности Гейзенберга
Поведение таких детерминированных систем тоже лучше описывается статистическими законами
Слайд 26Связь определений
Точка 0 – единственная критическая точка, т.е. точка, в которой
производная обращается в нуль
Согласно мощным результатам Жюлиа и Фату любой притягивающий или рационально нейтральный цикл содержит в своей области притяжения по крайней мере одну критическую точку
Тогда в случае, когда последовательность с началом в нуле устремляется в бесконечность циклы существовать не могут, а само множество Жюлиа превращается в пыль Фату
Согласно мощным результатам Жюлиа и Фату любой притягивающий или рационально нейтральный цикл содержит в своей области притяжения по крайней мере одну критическую точку
Тогда в случае, когда последовательность с началом в нуле устремляется в бесконечность циклы существовать не могут, а само множество Жюлиа превращается в пыль Фату
