- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Алгебра высказываний. Определение высказывания. Таблица истинности для высказываний. Логические тождества. (Лекция 2) презентация
Содержание
- 1. Алгебра высказываний. Определение высказывания. Таблица истинности для высказываний. Логические тождества. (Лекция 2)
- 2. 2. Определение высказывания. Таблица истинности для
- 3. Соглашение 1 Если высказывание сконструировано из однотипных
- 4. Соглашение 4 Конъюнкция связывает сильнее, чем дизъюнкция.
- 5. Примеры 1)Избавиться от лишних скобок
- 6. Определение 3 Таблица истинности для высказывания
- 7. Пример Построить таблицу истинности для высказывания
- 8. 3. Равносильные высказывания. Определение 1 Высказывания
- 9. Примеры Доказательство
- 10. Основные логические тождества Идемпотентные законы:
- 11. Законы Моргана: Закон двойного
- 12. Законы поглощения: Доказательство Доказательство 18) 19) 20) 21)
- 13. Тождества, содержащие константы:
Слайд 1Алгебра высказываний
Лекция 2
Цель: Дать определение высказывания, таблицы истинности.
Сформулировать основные логические
Слайд 22. Определение высказывания.
Таблица истинности для высказываний
Определение 1
Переменная А, принимающая
Обозначаться логические переменные будут заглавными латинскими буквами с индексами или без них:
Слайд 3Соглашение 1
Если высказывание сконструировано из однотипных операций, то они выполняются в
К примеру,
Соглашение 2
Отрицание подразумевает скобки
Соглашение 3
Внешние скобки не ставятся.
Слайд 4Соглашение 4
Конъюнкция связывает сильнее, чем дизъюнкция.
Например,
Соглашение 5
Дизъюнкция связывает сильнее, чем
Например,
Соглашение 6
Импликация связывает сильнее, чем эквивалентность.
Например,
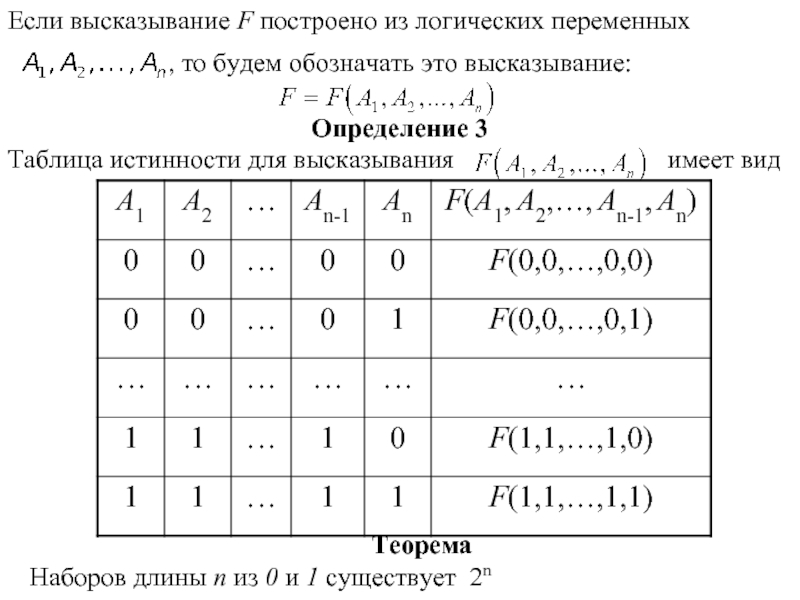
Слайд 6Определение 3
Таблица истинности для высказывания
Если высказывание F построено из логических переменных
, то будем обозначать это высказывание:
Теорема
Наборов длины n из 0 и 1 существует 2n
Слайд 83. Равносильные высказывания.
Определение 1
Высказывания F(A1,A2,…,An) и G(A1,A2,…,An) называются равносильными (или
имеет место равенство:
Обозначим
Другими словами, два высказывания равны, если у них совпадают таблицы истинности.
Слайд 10Основные логические тождества
Идемпотентные законы:
Коммутативные законы:
Ассоциативные законы:
1)
2)
3)
4)
5)
6)
7)
8)
Слайд 11Законы Моргана:
Закон двойного отрицания:
Закон противоречия:
Закон исключенного третьего:
9)
10)
11)
12)
13)
14)
15)
Дистрибутивные
16)
17)
Без названия: