- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Аксиомы стереометрии и их следствия презентация
Содержание
- 1. Аксиомы стереометрии и их следствия
- 2. Стереометрия Фигуры в пространстве Аксиомы стереометрии
- 3. Стереометрия – это раздел геометрии, в котором
- 4. Основные фигуры Геометрические тела Фигуры в пространстве
- 5. точка прямая плоскость Основные фигуры назад
- 6. куб Геометрические тела шар цилиндр параллелепипед пирамида конус назад
- 7. Аксиомы стереометрии А1 А2 А3 назад
- 8. Через любые три точки, не лежащие на
- 9. Если две точки прямой лежат в плоскости,
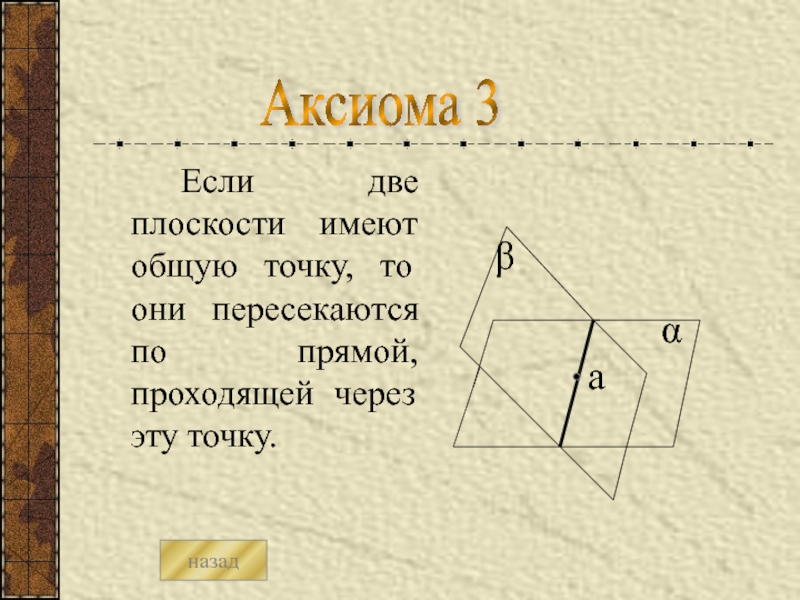
- 10. Если две плоскости имеют общую точку,
- 11. Следствия из аксиом стереометрии Теорема 1.1 Теорема 1.2 назад
- 12. Дано: Пр. а, т. М∉пр. а Доказать:
- 13. Дано: Пр. a и b пересекаются
- 14. Плоскость можно провести: Через три точки не
- 15. Две плоскости пересекаются. Сколько общих точек они
- 16. Даны плоскость α, точка А и прямая
- 17. Указать ошибочное утверждение: Если две плоскости
- 18. Какое из перечисленных утверждение верно: Любые
- 19. Сколько способов задания плоскости
- 20. Могут ли две плоскости иметь:
- 21. Верно ли утверждение: Если две точки окружности
- 22. неверно
- 23. верно
Слайд 2 Стереометрия
Фигуры в пространстве
Аксиомы стереометрии
Следствия из аксиом стереометрии
Способы задания плоскости
Контрольные вопросы
Аксиомы
стереометрии, и их следствия
Слайд 3 Стереометрия – это раздел геометрии, в котором изучаются свойства фигур в
пространстве.
«Стереос» - объёмный, пространственный и «метрео»- измерять.
«Стереос» - объёмный, пространственный и «метрео»- измерять.
Стереометрия
назад
Слайд 8 Через любые три точки, не лежащие на одной прямой, проходит плоскость,
и притом только одна.
Аксиома 1
назад
Слайд 9 Если две точки прямой лежат в плоскости, то все точки прямой
лежат в этой плоскости.
Аксиома 2
назад
Слайд 10 Если две плоскости имеют общую точку, то они пересекаются по
прямой, проходящей через эту точку.
Аксиома 3
назад
Слайд 12Дано:
Пр. а, т. М∉пр. а
Доказать:
1) Через прямую а и т.
М проходит плоскость α
2) α - единственная.
Доказательство:
а) Отметим на прямой а точки P и Q. б) Через точки P ,Q и М проведем плоскость α ( А1). в) По аксиоме А2 прямая а принадлежит плоскости α.
2) Плоскость α проходящая через прямую а и точку М совпадает с плоскостью проходящей через точки P, Q, М. По А1 такая плоскость единственная.
2) α - единственная.
Доказательство:
а) Отметим на прямой а точки P и Q. б) Через точки P ,Q и М проведем плоскость α ( А1). в) По аксиоме А2 прямая а принадлежит плоскости α.
2) Плоскость α проходящая через прямую а и точку М совпадает с плоскостью проходящей через точки P, Q, М. По А1 такая плоскость единственная.
назад
Теорема т. 1.1 Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
Слайд 13Дано:
Пр. a и b пересекаются в точке М.
Доказать:
Через прямые a
и b проходит плоскость α.
α - единственная.
Доказательство:
а) Отметим на прямой b точку N.
б) Через прямую а и точку N проведём плоскость α (Т1.1); т.к. точки М и N принадлежат α, следовательно b принадлежат α (А2).
Единственность такой плоскости, следует из того,что любая плоскость, проходящая через пр. а и b, проходит через прямую а т. N. Следовательно, она совпадает с плоскостью α, а по (Т1.1) такая плоскость единственная.
α - единственная.
Доказательство:
а) Отметим на прямой b точку N.
б) Через прямую а и точку N проведём плоскость α (Т1.1); т.к. точки М и N принадлежат α, следовательно b принадлежат α (А2).
Единственность такой плоскости, следует из того,что любая плоскость, проходящая через пр. а и b, проходит через прямую а т. N. Следовательно, она совпадает с плоскостью α, а по (Т1.1) такая плоскость единственная.
назад
Теорема т. 1.2 Через две пересекающиеся прямые проходит плоскость, и притом только одна.
Слайд 14Плоскость можно провести:
Через три точки не лежащие на одной прямой.
Через прямую
и не лежащую на ней точку.
Через две пересекающиеся прямые.
Через две параллельные прямые.
Через две пересекающиеся прямые.
Через две параллельные прямые.
Способы задания плоскости
назад
Слайд 15Две плоскости пересекаются. Сколько общих точек они имеют?
Одну
Две
Бесконечное множество
Контрольные вопросы
далее
Слайд 16Даны плоскость α, точка А и прямая а. А ∈ а,
а ∈α, тогда
т. А принадлежит
т. А не принадлежит
т.т. т. А. может лежать в плоскости , а может и не лежать в ней.
т. А принадлежит
т. А не принадлежит
т.т. т. А. может лежать в плоскости , а может и не лежать в ней.
Вопрос № 2
далее
Слайд 17Указать ошибочное утверждение:
Если две плоскости имеют общую прямую, то все
их общие точки лежат на этой прямой
Через три точки можно провести плоскость, и при том только одну
Если треугольник лежит в плоскости , то любая его медиана лежит в этой плоскости
Диагонали плоского четырехугольника лежит в плоскости этого четырехугольника
Через три точки можно провести плоскость, и при том только одну
Если треугольник лежит в плоскости , то любая его медиана лежит в этой плоскости
Диагонали плоского четырехугольника лежит в плоскости этого четырехугольника
Вопрос № 3
далее
Слайд 18Какое из перечисленных утверждение верно:
Любые три точки лежат в одной плоскости
Любые четыре точки лежат в одной плоскости
Любые четыре точки не лежат в одной плоскости
Через любые три точки проходит плоскость и при том только одна
Вопрос № 4
далее
Слайд 20Могут ли две плоскости иметь:
Только одну общую точку
Только две общие
точки
Только одну общую прямую
Только одну общую прямую
Вопрос № 6
далее
Слайд 21Верно ли утверждение:
Если две точки окружности лежат в плоскости, то и
вся окружность лежит в этой плоскости
Да
Нет
Да
Нет
Вопрос № 7
Всё
