Иванова Софья Андрияновна
Учитель: Стаханова Полина Александровна.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод вспомогательной окружности презентация
Содержание
- 1. Метод вспомогательной окружности
- 2. Цель: исследование метода вспомогательной окружности и его
- 3. Вспомогательная окружность - одно из
- 4. Докажем признаки при которых вокруг многоугольников можно
- 5. Второй признак: Если точки В
- 6. Третий признак: Четырёхугольник можно описать около
- 7. Углы, связанные с окружностью.
- 8. Угол между касательной и хордой, проведенными из
- 9. Отрезки, связанные с окружностью.
- 10. Отрезки касательных, проведенных к окружности из одной
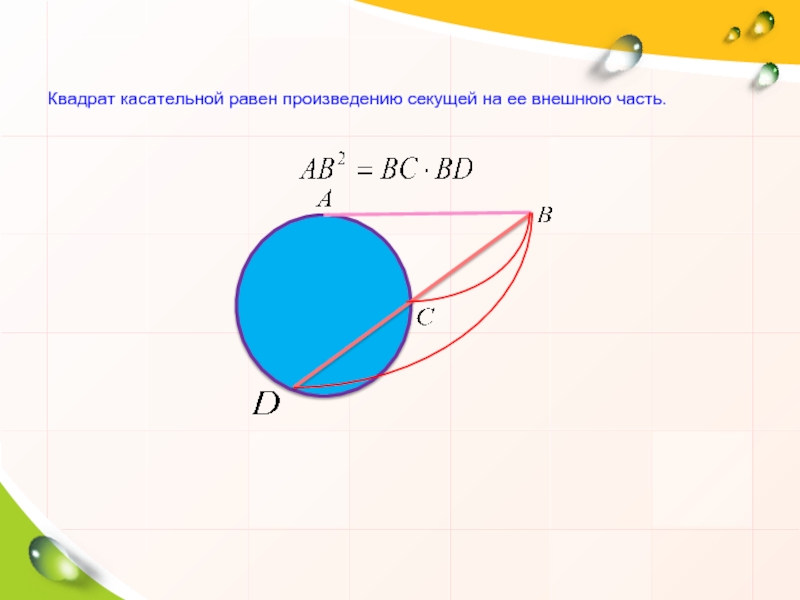
- 11. Квадрат касательной равен произведению секущей на ее внешнюю часть.
- 12. Задача№4: Расстояние между основаниями двух высот ВМ
- 13. Практическая часть: Решение задач с
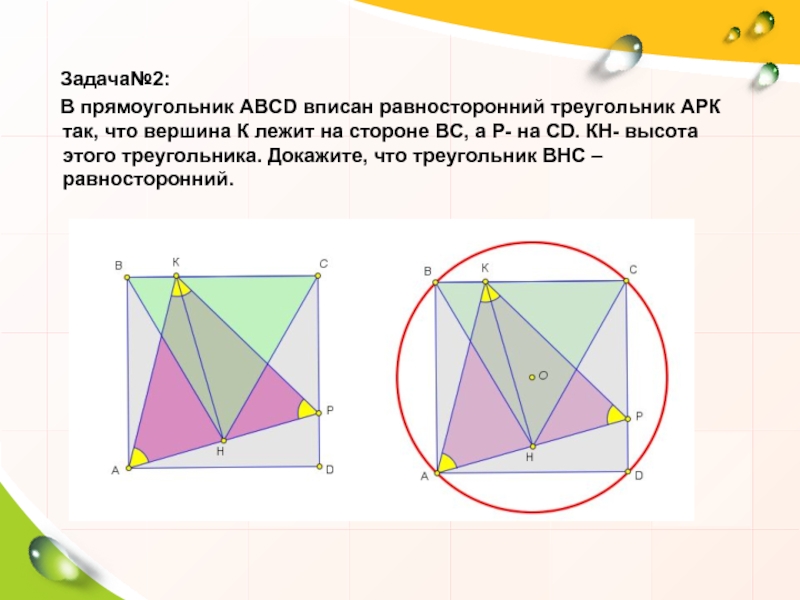
- 14. Задача№2:
- 15. В С 1.Вокруг
- 16. Задача№4: Расстояние между основаниями двух
- 17. Ответ: углы ромба равны 150°
- 18. Задача№5: Определить площадь трапеции, у
- 19. Задача №7(теорема о квадрате биссектрисы):
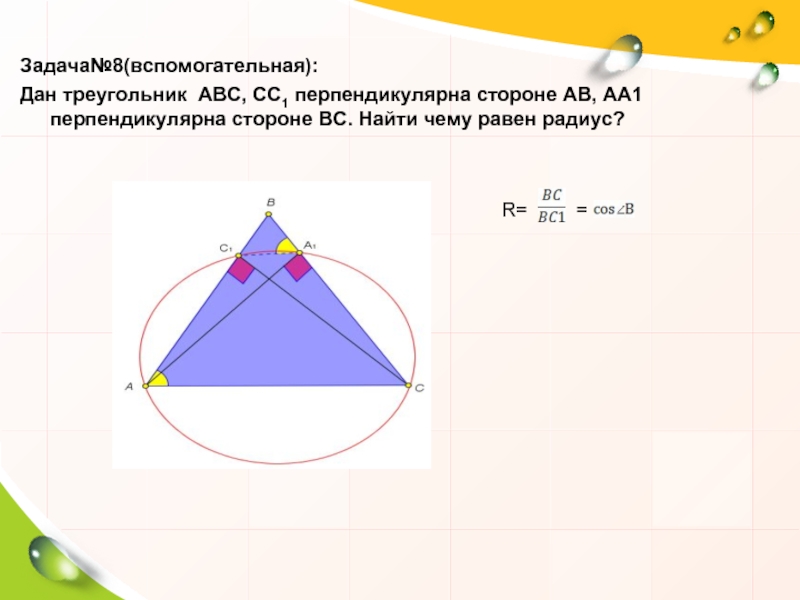
- 20. R= = Задача№8(вспомогательная): Дан
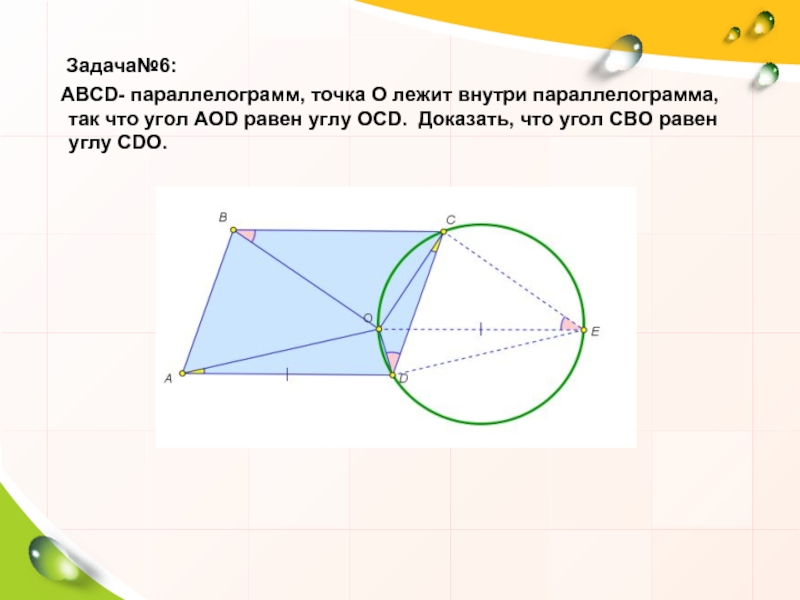
- 21. Задача№6: ABCD-
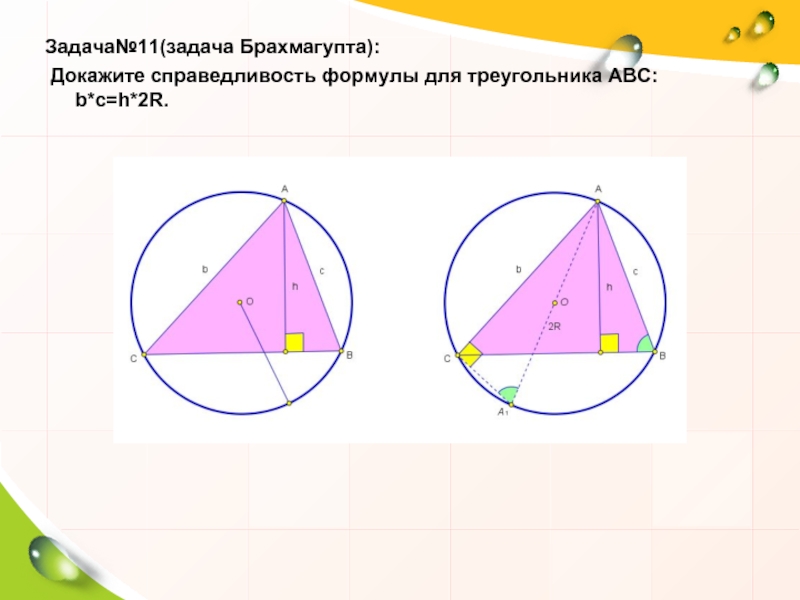
- 22. Задача№11(задача Брахмагупта): Докажите справедливость формулы для треугольника АВС: b*c=h*2R.
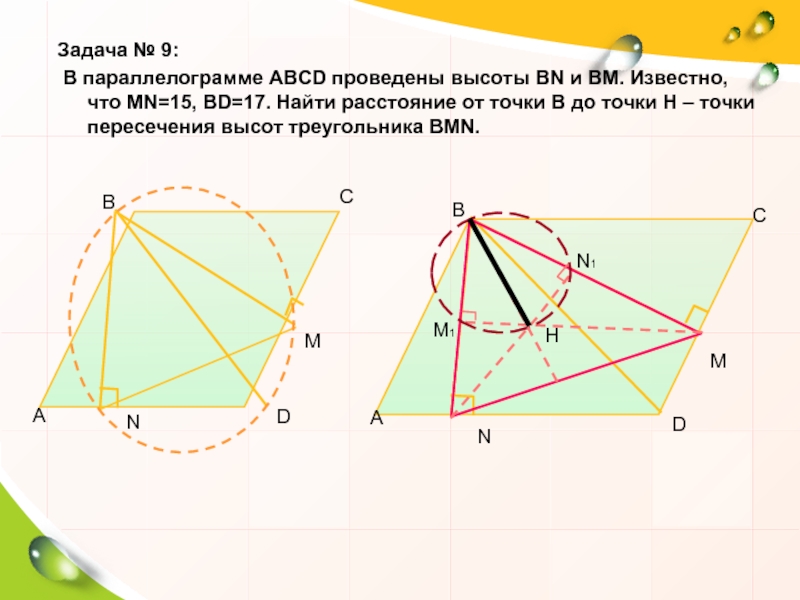
- 23. Задача № 9: В параллелограмме
- 24. “ Высшее проявление духа – это разум.
Цель: исследование метода вспомогательной окружности и его свойств, применение данного метода при решении задач. Методы исследования: 1.Изучение теории по вспомогательной окружности 2. Доказательство признаков задач, которые могут
Слайд 2Цель: исследование метода вспомогательной окружности и его свойств, применение данного метода
при решении задач.
Методы исследования:
1.Изучение теории по вспомогательной окружности
2. Доказательство признаков задач, которые могут привести к применению вспомогательной окружности
3. Установление связи между методом вспомогательной окружности и решением задач
4. Выполнение практической части.
Слайд 3 Вспомогательная окружность - одно из наиболее эстетичных дополнительных построений.
Метод вспомогательной окружности заключается в том, что если геометрическая фигура (многоугольник, треугольник, квадрат и т.п.) имеет ряд конкретных признаков, то вокруг неё можно описать окружность, что значительно облегчит решение ряда задач.
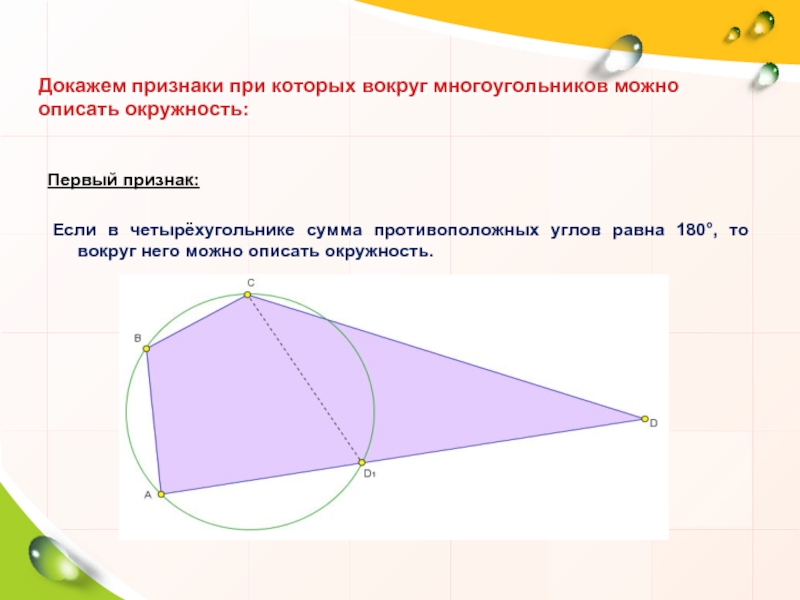
Слайд 4Докажем признаки при которых вокруг многоугольников можно описать окружность:
Первый признак:
Если в
четырёхугольнике сумма противоположных углов равна 180°, то вокруг него можно описать окружность.
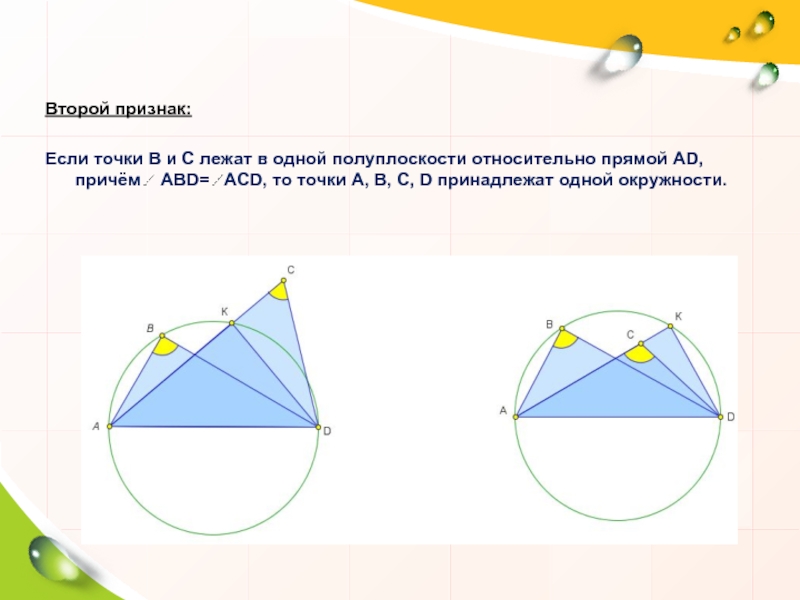
Слайд 5Второй признак:
Если точки В и С лежат в одной полуплоскости
относительно прямой AD, причём АВD= ACD, то точки A, B, C, D принадлежат одной окружности.
Слайд 6Третий признак:
Четырёхугольник можно описать около окружности тогда и только тогда, когда
суммы его противоположных сторон равны.
a + b = c + d.
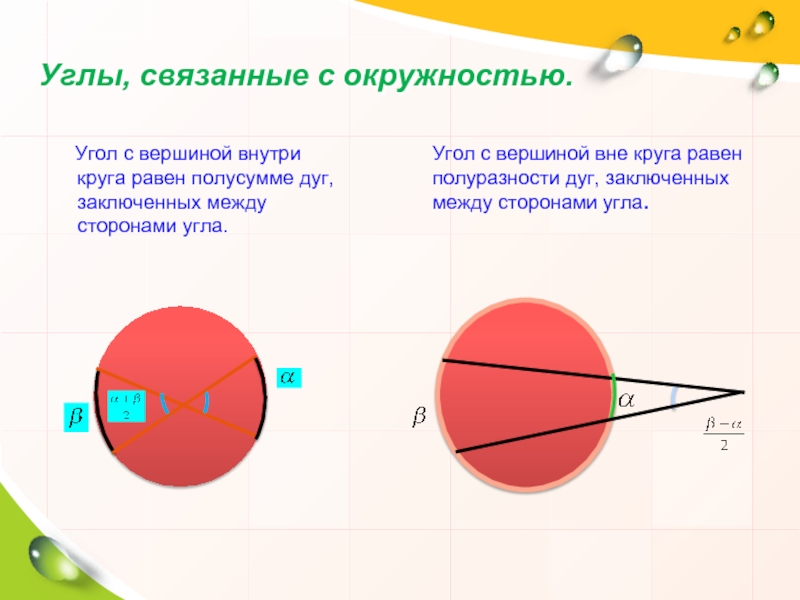
Слайд 7Углы, связанные с окружностью.
Угол с вершиной внутри
круга равен полусумме дуг, заключенных между сторонами угла.
Угол с вершиной вне круга равен полуразности дуг, заключенных между сторонами угла.
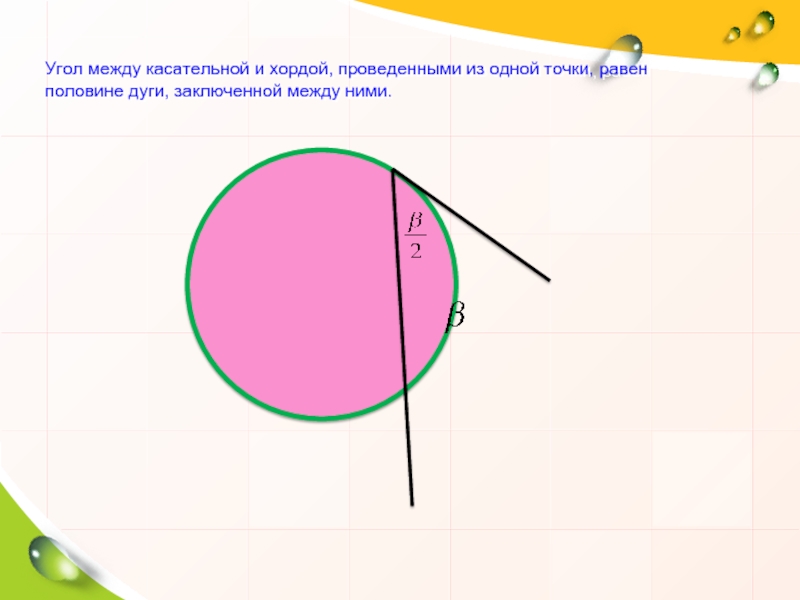
Слайд 8Угол между касательной и хордой, проведенными из одной точки, равен половине
дуги, заключенной между ними.
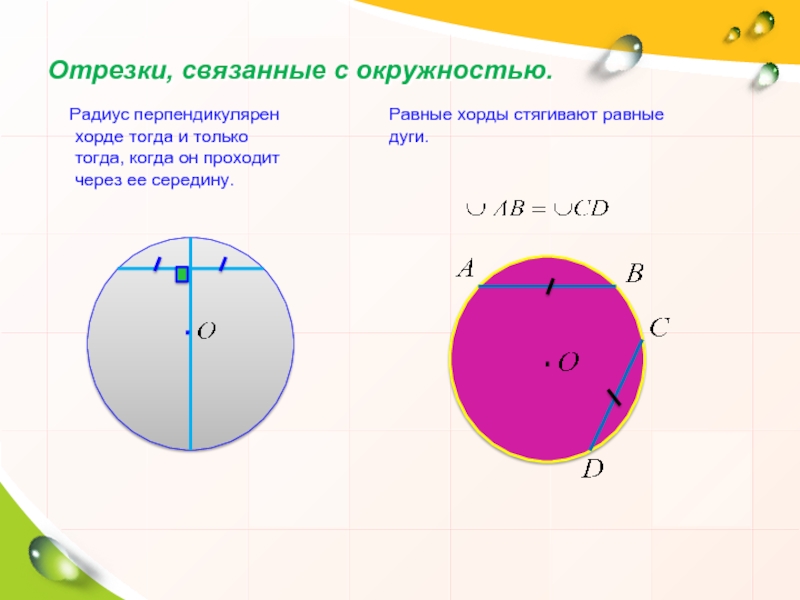
Слайд 9Отрезки, связанные с окружностью.
Радиус перпендикулярен хорде тогда и
только тогда, когда он проходит через ее середину.
Равные хорды стягивают равные дуги.
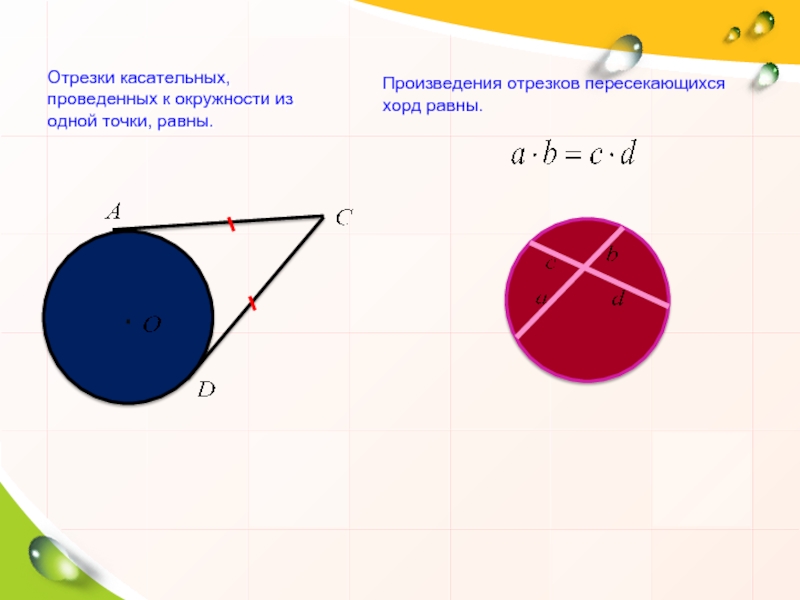
Слайд 10Отрезки касательных, проведенных к окружности из одной точки, равны.
Произведения отрезков пересекающихся
хорд равны.
Слайд 12Задача№4:
Расстояние между основаниями двух высот ВМ и BN ромба ABCD вдвое
меньше диагонали BD. Найдите углы ромба.
Первый случай:
Если угол В - тупой
Первый случай:
Если угол В - тупой
1.Вокруг ABCD- можно описать окружность.
2. BD- диаметр
3.так как 2MN= BD=> MN=R(где R- радиус).
4.∆MON-равносторонний
Ответ: углы ромба равны 150° и 30°.
Слайд 13
Практическая часть: Решение задач с помощью метода вспомогательной окружности.
Задача№1:
Дан прямоугольный треугольник АВС, С= 90°. На катете ВС выбрана произвольная точка М. Из точки М проведён перпендикуляр МN на гипотенузу АВ. Докажите, что ANC= AMC.
Дан прямоугольный треугольник АВС, С= 90°. На катете ВС выбрана произвольная точка М. Из точки М проведён перпендикуляр МN на гипотенузу АВ. Докажите, что ANC= AMC.
Слайд 14
Задача№2:
В прямоугольник ABCD вписан равносторонний треугольник
АРК так, что вершина К лежит на стороне ВС, а Р- на CD. КН- высота этого треугольника. Докажите, что треугольник ВНС – равносторонний.
Слайд 15
В
С
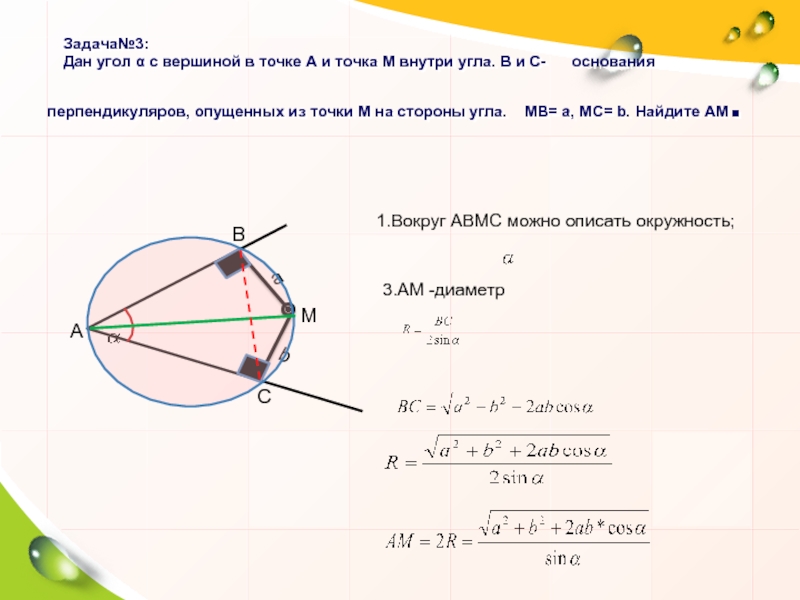
1.Вокруг АВМС можно описать окружность;
3.АМ -диаметр
Задача№3:
Дан угол α с вершиной
в точке А и точка М внутри угла. В и С- основания перпендикуляров, опущенных из точки М на стороны угла. МВ= a, МС= b. Найдите АМ.
Слайд 16
Задача№4:
Расстояние между основаниями двух высот ВМ и BN ромба ABCD вдвое
меньше диагонали BD. Найдите углы ромба.
Первый случай:
Если угол В - тупой
Первый случай:
Если угол В - тупой
1.Вокруг ABCD- можно описать окружность.
2. BD- диаметр
3.так как 2MN= BD=> MN=R(где R- радиус).
4.∆MON-равносторонний
Ответ: углы ромба равны 150° и 30°.
Слайд 17
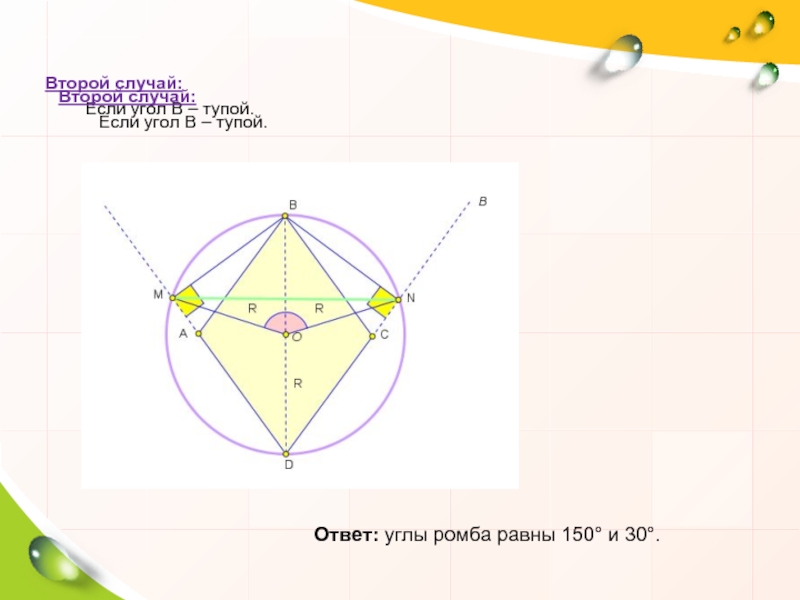
Ответ: углы ромба равны 150° и 30°.
Второй случай:
Если угол В –
тупой.
Второй случай:
Если угол В – тупой.
Слайд 18
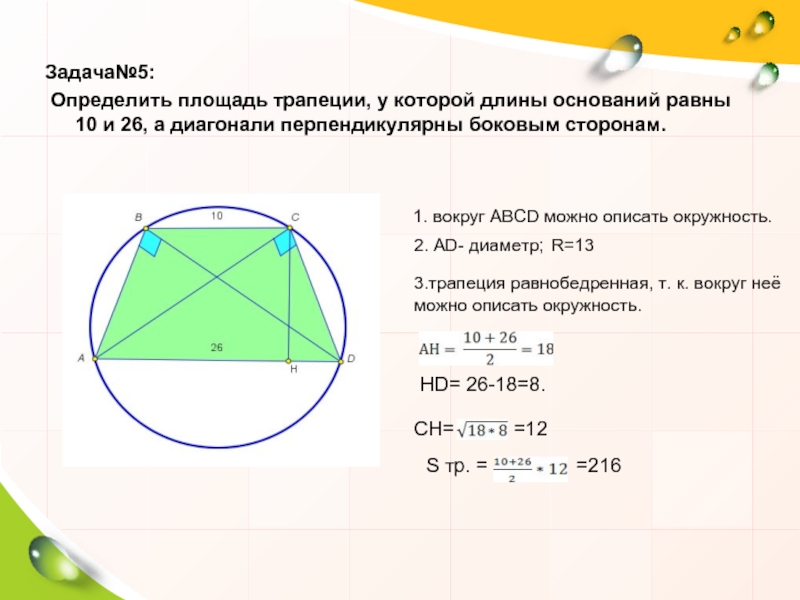
Задача№5:
Определить площадь трапеции, у которой длины оснований равны 10 и 26,
а диагонали перпендикулярны боковым сторонам.
1. вокруг ABCD можно описать окружность.
2. AD- диаметр;
R=13
3.трапеция равнобедренная, т. к. вокруг неё можно описать окружность.
HD= 26-18=8.
СН=
=12
S тр. =
=216
Слайд 19
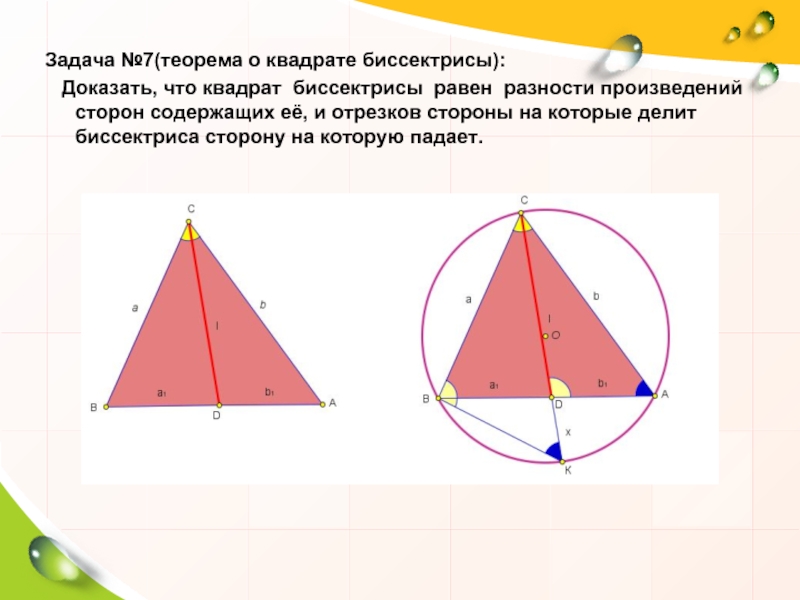
Задача №7(теорема о квадрате биссектрисы):
Доказать, что
квадрат биссектрисы равен разности произведений сторон содержащих её, и отрезков стороны на которые делит биссектриса сторону на которую падает.
Слайд 20
R=
=
Задача№8(вспомогательная):
Дан треугольник АВС, СС1 перпендикулярна стороне АВ, АА1 перпендикулярна стороне
ВС. Найти чему равен радиус?
Слайд 21 Задача№6:
ABCD- параллелограмм, точка О лежит внутри
параллелограмма, так что угол AOD равен углу OCD. Доказать, что угол СВО равен углу CDO.
Слайд 22
Задача№11(задача Брахмагупта):
Докажите справедливость формулы для треугольника АВС: b*c=h*2R.
Слайд 23
Задача № 9:
В параллелограмме АВСD проведены высоты ВN и ВМ. Известно,
что МN=15, ВD=17. Найти расстояние от точки В до точки Н – точки пересечения высот треугольника ВМN.
Слайд 24“ Высшее проявление духа – это разум. Высшее проявление разума –
это геометрия. Клетка геометрии – треугольник. Он так же неисчерпаем, как и Вселенная. Окружность – душа геометрии. Познайте окружность, и вы не только познаете душу геометрии, но и возвысите душу свою”.
И.Ф. Шарыгин
www.themegallery.com
