- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Нам без чисел НИКУДА презентация
Содержание
- 1. Нам без чисел НИКУДА
- 4. "Все есть число", — говорили пифагорийцы
- 5. Простая система счисления У первобытных людей
- 6. Основание системы счисления – это число,
- 7. Десятеричная и пятеричная система возникла от
- 8. Древнеегипетская десятичная Примерно в третьем
- 10. 100. Это мерная веревка, которой измеряли
- 11. Десятичную систему счисления ввели римляне. Римские
- 12. Это, наверное, самая известная система, после
- 13. Предполагаемое происхождение римских цифр
- 14. Древнегреческая аттическая пятеричная В
- 15. Древнегреческая ионийская десятеричная алфавитная Примерно в
- 16. Славянская глаголическая десятеричная Эта система
- 18. Славянская кириллическая десятеричная алфавитная Эта нумерация
- 20. Для обозначения чисел больших, чем 900
- 21. Древнеиндийские системы счисления
- 22. Вавилонская десятеричная / шестидесятеричная В древнем
- 23. Древнекитайская десятеричная Эта система одна из
- 24. Двадцатеричная система счисления индейцев Майя или
- 26. История «арабских» чисел. История наших привычных
- 28. История нуля. Нуль бывает разный. Во-первых,
- 29. Нуль - это уникальный знак. Нуль
- 30. Над презентацией
- 31. Список использованной литературы 1. В. Лёвшин,
Слайд 4
"Все есть число", — говорили пифагорийцы (ученики древнегреческого математика Пифагора). Значит
Число - это обобщение, так как разными числами можно подсчитать разные предметы.
Цифры – это значки, с помощью которых записывают числа. Система счисления или нумерация – это способ записи чисел с помощью цифр.
Слайд 5
Простая система счисления
У первобытных людей не было даже чисел, они количество
Слайд 6
Основание системы счисления – это число, на основе которого ведется счет.
Слайд 7
Десятеричная и пятеричная система возникла от того факта, что на одной
Слайд 8
Древнеегипетская десятичная
Примерно в третьем тысячелетии до нашей эры древние египтяне
. Как и большинство людей для счета небольшого количества предметов Египтяне использовали палочки.
Слайд 10
100. Это мерная веревка, которой измеряли земельные участки после разлива Нила.
10
Слайд 11
Десятичную систему счисления ввели римляне. Римские цифры до сих пор используют
Слайд 12
Это, наверное, самая известная система, после «арабской», она возникла более двух
Слайд 14
Древнегреческая аттическая пятеричная
В древнейшее время в Греции была распространена так
В этой системе числа 1, 2, 3, 4 изображались соответствующим количеством вертикальных полосок: , , , . Число 5 записывалось знаком (древнее начертание буквы "Пи", с которой начиналось слово "пять" - "пенте"). Числа 6, 7, 8, 9 обозначались сочетаниями этих знаков:
Слайд 15
Древнегреческая ионийская десятеричная алфавитная
Примерно в третьем веке до нашей эры аттическая
Слайд 16
Славянская глаголическая десятеричная
Эта система была создана для обозначения чисел в
Слайд 18
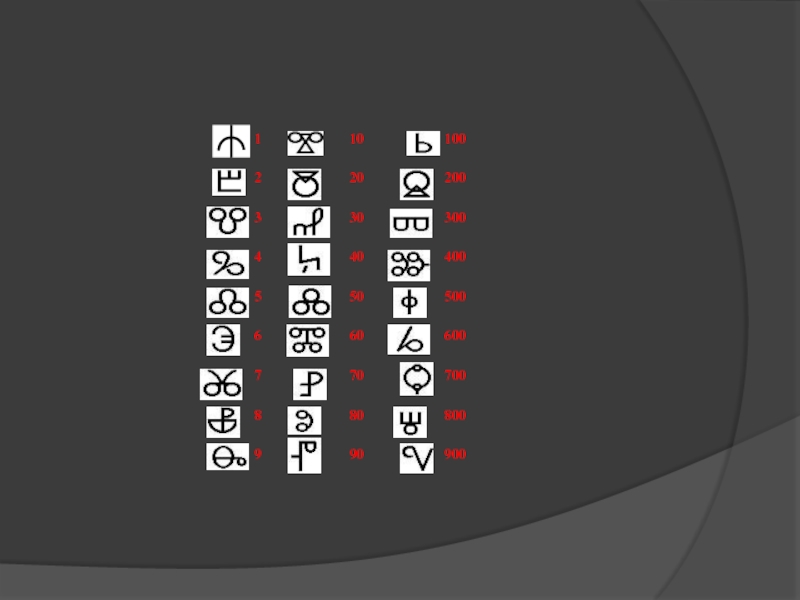
Славянская кириллическая десятеричная алфавитная
Эта нумерация была создана вместе со славянской алфавитной
Слайд 20
Для обозначения чисел больших, чем 900 использовались специальные значки, которые дорисовывались
Тысяча
1000
Тьма
10 000
Легион
100 000
Леодр
1 000 000
Ворон
10 000 000
Колода
100 000 000
Слайд 22
Вавилонская десятеричная / шестидесятеричная
В древнем Вавилоне примерно во II тысячелетие до
Слайд 23
Древнекитайская десятеричная
Эта система одна из старейших и самых прогрессивных, поскольку в
Слайд 24
Двадцатеричная система счисления индейцев Майя или долгий счет
Эта система очень интересна
Слайд 26
История «арабских» чисел.
История наших привычных «арабских» чисел очень запутана. Нельзя сказать
Слайд 28
История нуля.
Нуль бывает разный. Во-первых, нуль – это цифра, которая используется
Слайд 29
Нуль - это уникальный знак. Нуль – это чисто абстрактное понятие,
Слайд 30
Над презентацией
работали.
1.Глава проекта:
2.Помощница:Жариково Маша.
3.Технический сотрудник: Зоалкфл Даниаль
Слайд 31Список использованной литературы
1. В. Лёвшин, Три дня в Карликании, 1966
2. Всевозможные нумерации
3. А.П.Юшкевич, История математики, Том 1, 1970
4. Г. И. Глейзер, История математики в школе, 1964
5. И. Я. Депман, История арифметики, 1965
6.А.Костинский,В.Губайловский,Триединыйнуль (http://www.svoboda.org/programs/sc/2004/sc.011304.asp)
7. Кузьмищев В. А. Тайна жрецов майя. 2-е изд. — М., «Молодая гвардия», 1975