значения ЦФ, зависящей от n переменных.
Точка Х0 является точкой максимума, если в ее окрестностях значение функции f(X) не превосходит f(Х0). Для минимума - f(Х)≤f(Х0).
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задачи нелинейного программирования презентация
Содержание
- 1. Задачи нелинейного программирования
- 2. Рассмотрим функцию f(X) на отрезке [a,b]. .
- 3. Необходимое условие существования экстремума функции f(x) в
- 4. Методы решения задач НП
- 5. Аналитические методы Основаны на использовании необходимых
- 6. Численные методы Для поиска экстремума функции,
- 7. Покоординатные методы Отыскание экстремального значения функции по каждой из переменных.
- 8. Методы случайного поиска Выбирается любое допустимое
- 9. Градиентные методы Основаны на использовании градиента
- 10. Непрямые методы Сведение задачи НП к более
- 11. Методы квадратичного программирования Целевая функция представляет собой
- 12. Методы сепарабельного программирования Функции ограничений сепарабельны:
- 13. Методы геометрического программирования. Целевая функция и
- 14. Методы стохастического программирования. Целевая функция и
- 15. Общая задача нелинейного программирования формулируется
- 16. Вектор удовлетворяющий системе ограничений называется
- 17. Факторы, затрудняющие решение задач нелинейного программирования. В
- 18. Для задачи ЛП множество допустимых решений задачи
- 19. В ЛП множество точек, в которых ЦФ
- 20. Геометрический метод решения задач НП Если
- 21. Решение задачи нелинейного программирования графическим способом :
- 22. Определяют гиперповерхность наивысшего (наинизшего) уровня или устанавливают
- 23. Пример. Найти максимальное и минимальное значение функции При выполнении условий
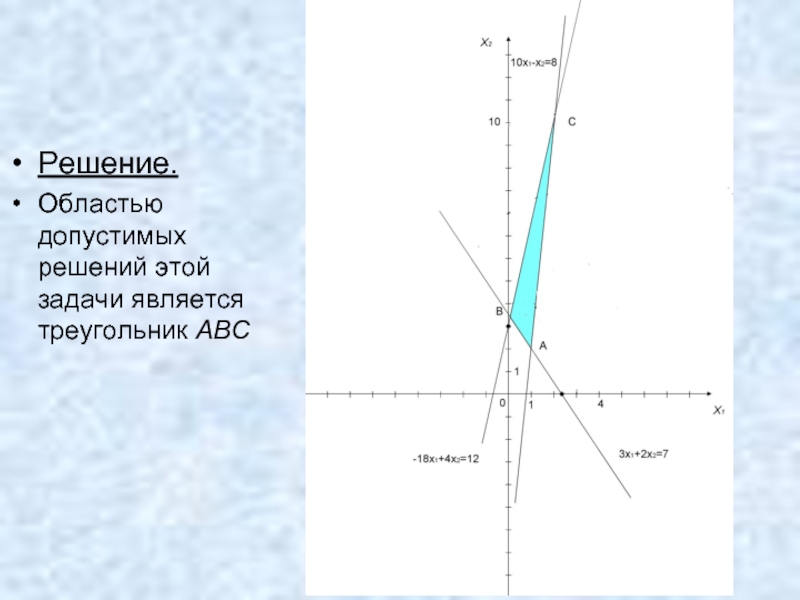
- 24. Решение. Областью допустимых решений этой задачи является треугольник ABC
- 25. Полагая значение целевой функции F
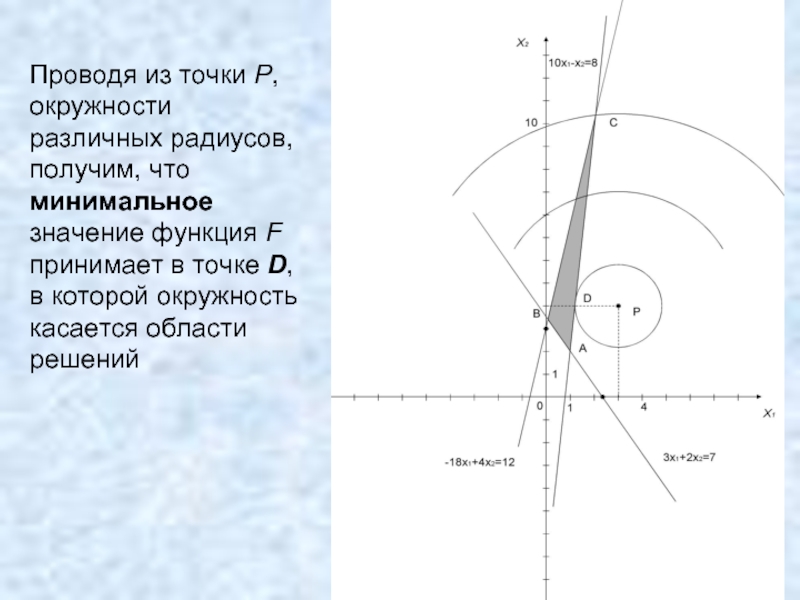
- 26. Проводя из точки P, окружности различных радиусов,
- 27. Координаты точки D определяются из равенства угловых
- 28. Рассматривая X2 как неявную функцию от переменной
- 29. получим систему: Решая систему, получим
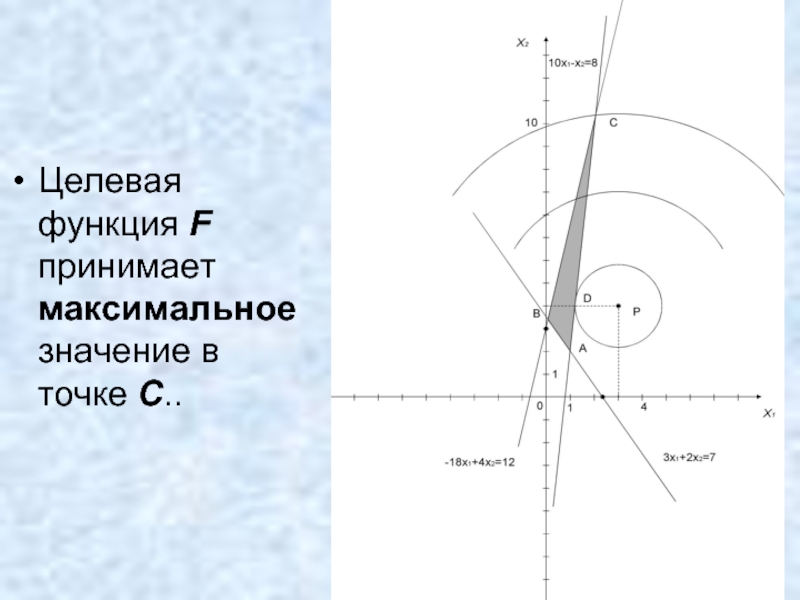
- 30. Целевая функция F принимает максимальное значение в точке C..
- 31. Координаты точки C находят решая систему уравнений,
Рассмотрим функцию f(X) на отрезке [a,b]. . а в f(x5)-глобальный максимум, f(x1), f(x3) – локальные максимумы. f(x1) – нестрогий максимум. x2 , x4 – точки минимумов.
Слайд 2Рассмотрим функцию f(X) на отрезке [a,b]. .
а
в
f(x5)-глобальный максимум, f(x1), f(x3) –
локальные максимумы.
f(x1) – нестрогий максимум. x2 , x4 – точки минимумов.
f(x1) – нестрогий максимум. x2 , x4 – точки минимумов.
Слайд 3Необходимое условие существования экстремума функции f(x) в точке x0 является равенство
нулю градиента функции в этой точке grad f(x0)=0
grad f(X)=(df/dx1,……..df/dxn) – задает угол наклона касательной к графику функции.
Это условие не является достаточным, т.к. оно выполняется для точек перегиба и седловых точек, их называют стационарными точками.
grad f(X)=(df/dx1,……..df/dxn) – задает угол наклона касательной к графику функции.
Это условие не является достаточным, т.к. оно выполняется для точек перегиба и седловых точек, их называют стационарными точками.
Слайд 5Аналитические методы
Основаны на использовании необходимых и достаточных условий экстремумов функций.
Для их использования необходимо, чтобы ЦФ и функции ограничений были непрерывными вместе с их частными производными первого порядка.
Слайд 6Численные методы
Для поиска экстремума функции, зависящей от 1-й переменной.
Выделяется
диапазон значений x , на котором может находиться точка экстремума, затем диапазон сужается до тех пор, пока не будет найдена точка экстремума с заданной точностью
Слайд 8Методы случайного поиска
Выбирается любое допустимое решение.
Переход к следующему решению
производится в случайным образом выбранном направлении.
Если при этом получаем улучшенное значение целевой функции, то дальше движемся в выбранном направлении, иначе – меняем направление.
В результате получаем приближенное решение с заданной точностью.
Если при этом получаем улучшенное значение целевой функции, то дальше движемся в выбранном направлении, иначе – меняем направление.
В результате получаем приближенное решение с заданной точностью.
Слайд 9Градиентные методы
Основаны на использовании градиента ЦФ (градиент в точке указывает
направление скорейшего возрастания функции).
Пошаговый переход от одного допустимого решения к другому в направлении градиента.
Получаем приближенное решение с заданной точностью. Это наиболее универсальные методы.
Пошаговый переход от одного допустимого решения к другому в направлении градиента.
Получаем приближенное решение с заданной точностью. Это наиболее универсальные методы.
Слайд 10Непрямые методы
Сведение задачи НП к более простой задаче, например задаче ЛП.
В зависимости от вида ЦФ и функций ограничений выделяют следующие классы
Слайд 11Методы квадратичного программирования
Целевая функция представляет собой сумму линейной функции и квадратичной
формы, а функции ограничений являются линейными функциями.
F=∑cjxj+∑∑aikxjxk
j=1,n k=1,n
F=∑cjxj+∑∑aikxjxk
j=1,n k=1,n
Слайд 12Методы сепарабельного программирования
Функции ограничений сепарабельны:
F(x1….xn)=F1(x1)+…+Fn(xn)
Методы решения основаны на линейной аппроксимации
ЦФ и применении симплекс-метода.
Слайд 13Методы геометрического программирования.
Целевая функция и функции ограничений являются полиномами и
имеют следующий вид:
F=∑uk
F=∑uk
ck- положительны, aki- целые числа.
Слайд 14Методы стохастического программирования.
Целевая функция и функции ограничений являются линейными, но
при этом коэффициенты aij, bi – случайные числа, а ограничения должны выполняться с некоторыми вероятностями.
Слайд 15 Общая задача нелинейного программирования формулируется следующим образом: найти вектор
удовлетворяющий системе ограничений:
и обращающий в максимум (или минимум) целевую функцию
Слайд 16Вектор
удовлетворяющий системе ограничений называется допустимым решением задачи нелинейного программирования
Допустимое
решение, при котором целевая функция F достигает максимального значения (в случае задачи максимизации) или минимального значения (в случае задачи минимизации) называется оптимальным.
Слайд 17Факторы, затрудняющие решение задач нелинейного программирования.
В задачах ЛП ЦФ имеет абсолютный
глобальный экстремум, в НП ЦФ может иметь несколько локальных экстремумов, при этом не существует методов, с помощью которых можно установить, является ли этот экстремум глобальным
Слайд 18Для задачи ЛП множество допустимых решений задачи образует выпуклый многогранник, при
этом оптимальное решение достигается в одной из его вершин, т.е. за конечное число шагов мы можем найти оптимальное решение (если оно существует).
В НП множество допустимых решений образует область, которая не всегда выпукла. Оптимальное решение может находиться не только на границе области, но и в любой внутренней точке. Следовательно, его нельзя найти с помощью перебора.
В НП множество допустимых решений образует область, которая не всегда выпукла. Оптимальное решение может находиться не только на границе области, но и в любой внутренней точке. Следовательно, его нельзя найти с помощью перебора.
Слайд 19В ЛП множество точек, в которых ЦФ принимает постоянное значение есть
гиперплоскость c1x1+……cnxn=const. При различных значениях const мы получаем параллельные гиперплоскости.
В НП множество точек, в которых ЦФ принимает постоянное значение есть гиперповерхность f(x1……xn)=const. При различных значениях const мы получаем гиперповерхности, которые могут пересекаться.
В НП множество точек, в которых ЦФ принимает постоянное значение есть гиперповерхность f(x1……xn)=const. При различных значениях const мы получаем гиперповерхности, которые могут пересекаться.
Слайд 20Геометрический метод решения задач НП
Если определена область допустимых решений, то
нахождение решения задачи нелинейного программирования сводится к определению такой точки этой области, через которую проходит гиперповерхность наивысшего уровня (в случае максимизации) или наинизшего уровня (в случае минимизации):
Слайд 21Решение задачи нелинейного программирования графическим способом :
Находят область допустимых решений задачи.
Если она пуста, то задача решения не имеет.
Строят гиперповерхность .
Строят гиперповерхность .
Слайд 22Определяют гиперповерхность наивысшего (наинизшего) уровня или устанавливают неразрешимость задачи из-за неограниченности
функции F сверху (снизу) на множестве допустимых решений.
Находят точку области допустимых решений, через которую проходит гиперповерхность наивысшего (наинизшего) уровня, и определяют значение целевой функции F в этой точке
Находят точку области допустимых решений, через которую проходит гиперповерхность наивысшего (наинизшего) уровня, и определяют значение целевой функции F в этой точке
Слайд 25
Полагая значение целевой функции F равным некоторому числу h, получаем
линии уровня
которые являются окружностями с центром P(3, 4) и радиусом h. С увеличением (уменьшением) h значения функции F соответственно увеличиваются (уменьшаются).
Слайд 26Проводя из точки P, окружности различных радиусов, получим, что минимальное значение
функция F принимает в точке D, в которой окружность касается области решений
Слайд 27Координаты точки D определяются из равенства угловых коэффициентов прямой
Из уравнения
прямой видим, что ее угловой коэффициент в точке D равен 10.
Угловой коэффициент касательной к окружности в точке D определим как значение производной функции x2 от переменной x1 в этой точке
Угловой коэффициент касательной к окружности в точке D определим как значение производной функции x2 от переменной x1 в этой точке
и касательной к окружности в точке D.
Слайд 28Рассматривая X2 как неявную функцию от переменной X1 и дифференцируя уравнение
окружности, получим
откуда
