- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задача линейного программирования и способы решения презентация
Содержание
- 1. Задача линейного программирования и способы решения
- 2. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ Общей задачей линейного программирования называется
- 3. АКТУАЛЬНОСТЬ ПРОБЛЕМЫ Использование метода линейного программирования представляет
- 4. ГРАФИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ Если ограничение
- 5. Графическая интерпретация целевой функции Графическим отображением целевой
- 6. ВАРИАНТЫ РЕШЕНИЯ Бесконечное множество решений Целевая
- 7. РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАМИРОВАНИЯ В EXCEL
- 8. МАТЕАМТИЧЕСКАЯ МОДЕЛЬ
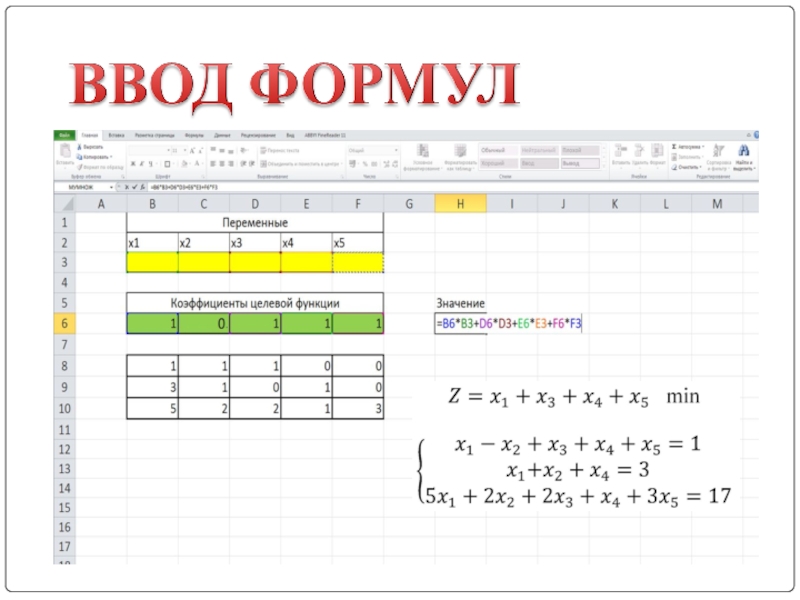
- 11. ВВОД ФОРМУЛ
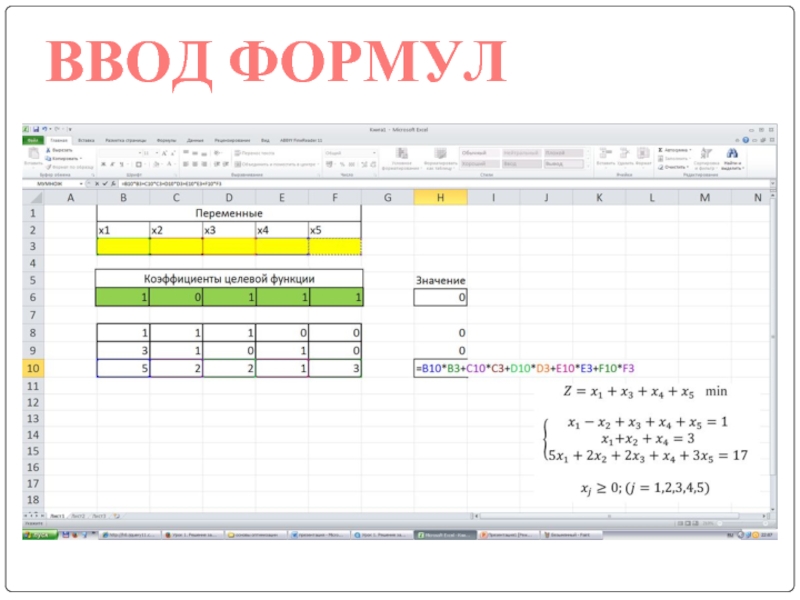
- 12. ВВОД ФОРМУЛ
- 13. ВВОД ЗНАЧЕНИЙ ОГРАНИЧЕНИЙ РАВЕНСТВ
- 14. ВЫБИРАЕМ НАДСТРОЙКУ ПОИСК РЕШЕНИЯ
- 15. ЗАПОЛНЯЕМ ДИАЛОГОВОЕ ОКНО
- 16. ЗАПОЛНЯЕМ ДИАЛОГОВОЕ ОКНО
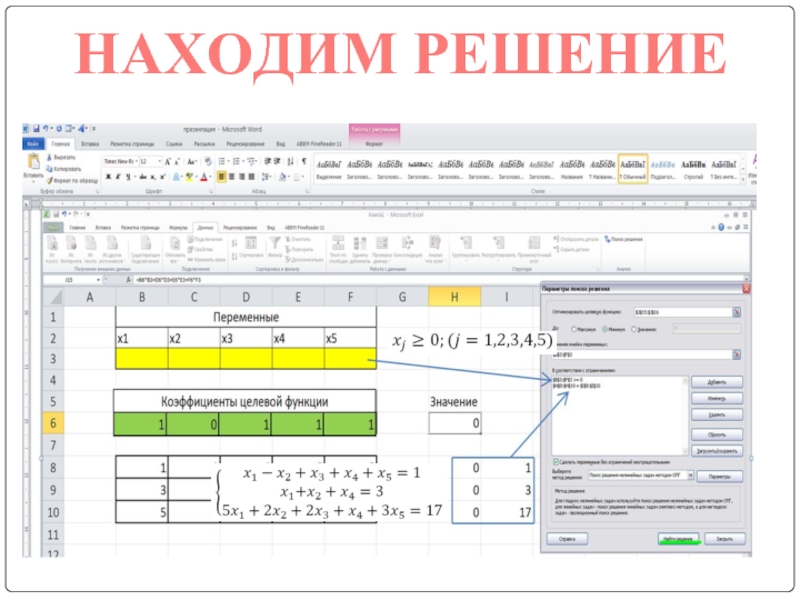
- 17. НАХОДИМ РЕШЕНИЕ
- 18. СОХРАНЯЕМ НАЙДЕННОЕ РЕШЕНИЕ
- 19. С помощью задач линейного программирования
Слайд 2ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Общей задачей линейного программирования называется задача, которая состоит в определении
Область математического программирования, изучающая методы решения оптимизационных задач, в которых и целевая функция, и ограничения задачи представлены линейными выражениями.
Математическая модель любой задачи линейного программирования включает в себя:
максимум или минимум целевой функции (критерий оптимальности);
систему ограничений в форме линейных уравнений и неравенств;
требование неотрицательности переменных.
Слайд 3АКТУАЛЬНОСТЬ ПРОБЛЕМЫ
Использование метода линейного программирования представляет собой важность и ценность -
Актуальность и значимость линейного программирования заключается в его способности решить широкий круг вопросов и проблем экономики по поиску наилучшего решения. В частности линейное программирование используется в таких сферах, как планирование электроснабжения города (района), планирование производства предприятия, оптимальной нагрузки оборудования и так далее.
ЗАПИСЬ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ В КРАТКОЙ ФОРМЕ
Задача линейного программирования
задана в канонической форме,
если:
все ограничения, входящие в систему –уравнения;
на все переменные наложены условия неотрицательности.
Слайд 4ГРАФИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Если ограничение задано равенством, то геометрически оно
Если ограничение задано неравенством, то геометрически оно может быть представлено полуплоскостью.
Множество точек на плоскости, удовлетворяющих системе ограничений, составляет выпуклую многоугольную область.
Область допустимых решений имеет вид неограниченного выпуклого многоугольника.
Если неравенства противоречат друг другу, и допустимая область пуста, задача решений не имеет.
Слайд 5Графическая интерпретация целевой функции
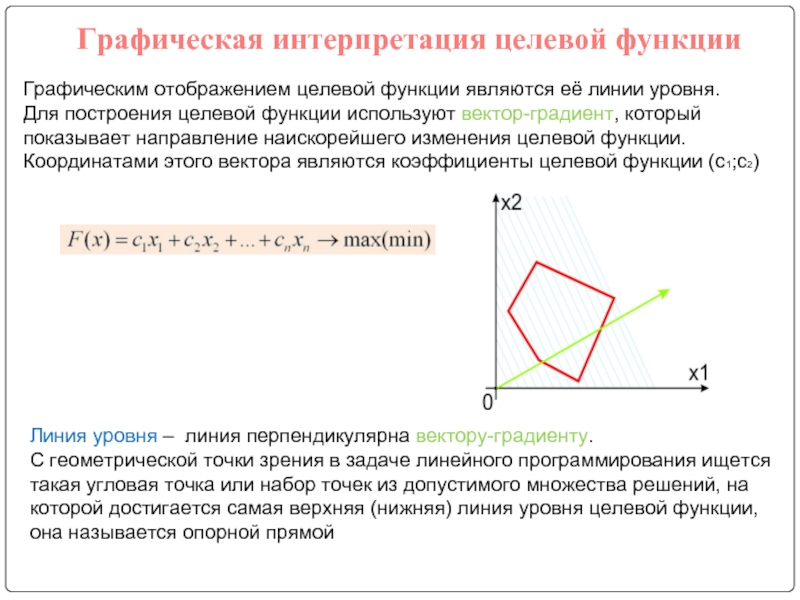
Графическим отображением целевой функции являются её линии уровня.
Для построения целевой функции используют вектор-градиент, который показывает направление наискорейшего изменения целевой функции. Координатами этого вектора являются коэффициенты целевой функции (с1;с2)
Линия уровня – линия перпендикулярна вектору-градиенту.
С геометрической точки зрения в задаче линейного программирования ищется такая угловая точка или набор точек из допустимого множества решений, на которой достигается самая верхняя (нижняя) линия уровня целевой функции, она называется опорной прямой
Слайд 6ВАРИАНТЫ РЕШЕНИЯ
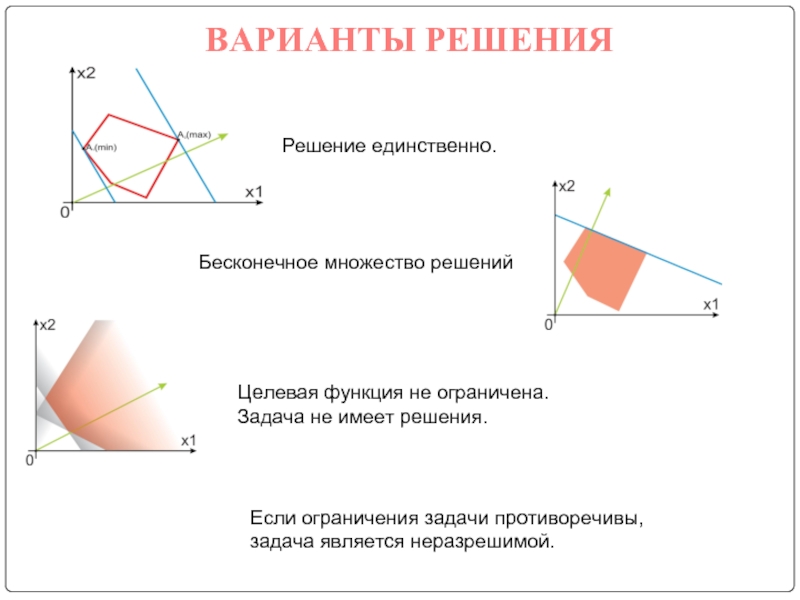
Бесконечное множество решений
Целевая функция не ограничена.
Задача не имеет
Решение единственно.
Если ограничения задачи противоречивы, задача является неразрешимой.