- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вычислительные машины презентация
Содержание
- 1. Вычислительные машины
- 2. Учебно-методические материалы Точи Р.Дж., Уидмер Н.С. Цифровые
- 3. Путков В.Н. и др. Электронные вычислительные устройства:
- 4. Позиционные системы счисления. Позиционная система счисления
- 5. Пусть - число в системе счисления с
- 6. В вычислительной технике применяется двоичная система (X
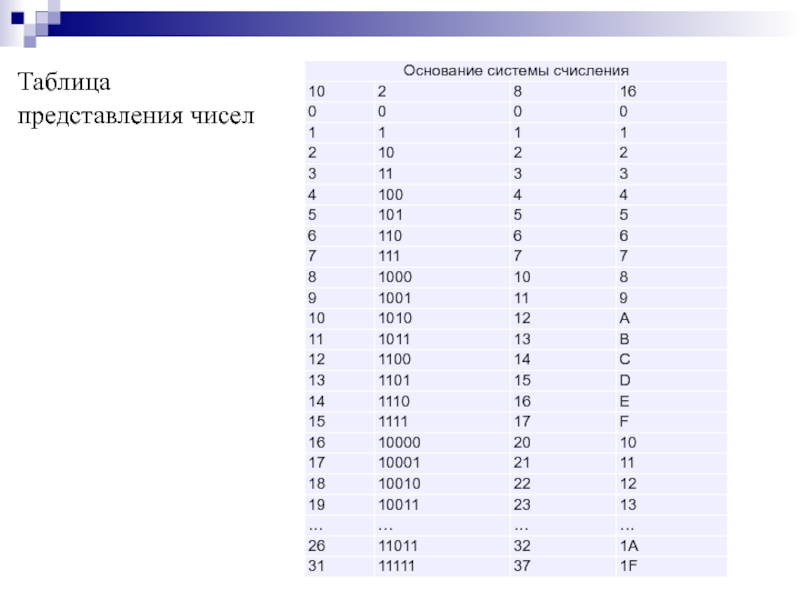
- 7. Таблица представления чисел
- 8. Пример двоично-десятичного кода 0001 1001 1000 0100(D)
- 9. Правило перевода целых чисел. Пример. Перевести целое
- 10. Перевод из недесятичной позиционной системы счисления в
- 11. Перевод дробей Пример. Перевести десятичную дробь 0,375
- 12. Пример: десятичной дроби 0,7689 соответствует двоичная дробь
- 13. Перевод неправильной дроби Пример. Последовательно перевести число
- 14. Перевод (2) ? (16) (0001)(0101)(0100),(1100)
- 15. Основы алгебры логики Рассмотрим некоторую функцию y
- 16. Число всех булевых функций, зависящих от n
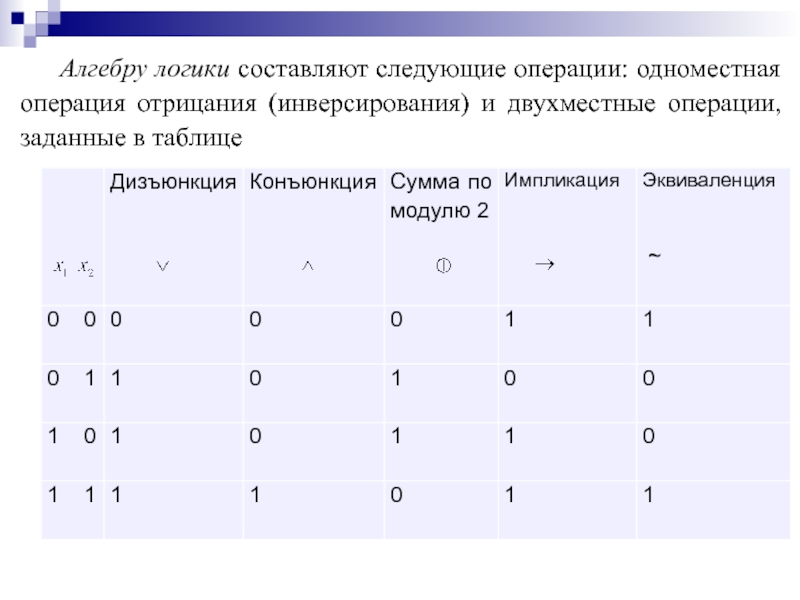
- 17. Алгебру логики составляют следующие операции: одноместная операция отрицания (инверсирования) и двухместные операции, заданные в таблице
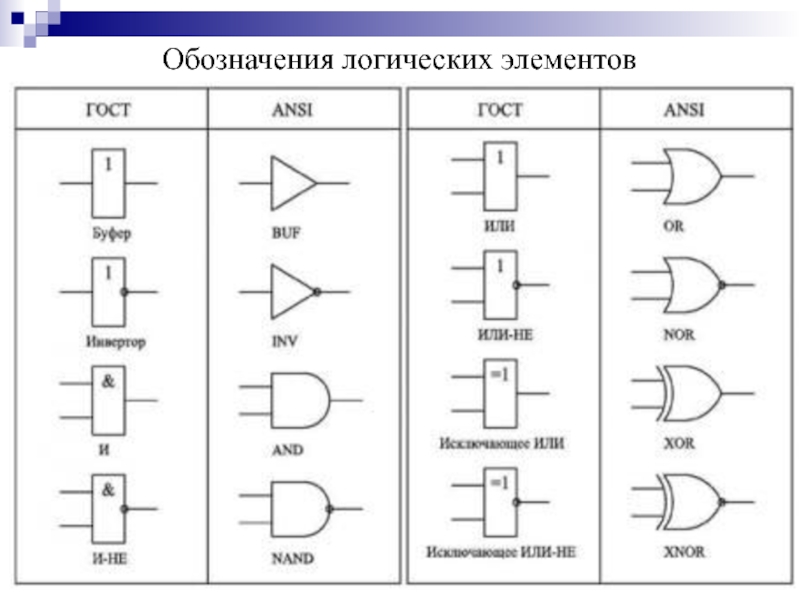
- 18. Обозначения логических элементов
- 19. Основные законы и аксиомы (тождества) алгебры логики.
- 20. Коммутативность Ассоциативность Дистрибутивность Поглощение Законы де Моргана
- 21. Аналитическое представление булевых функций Табличное задание
- 22. Пример табличного задания функции от трех аргументов. Три функции, зависящие от двух аргументов
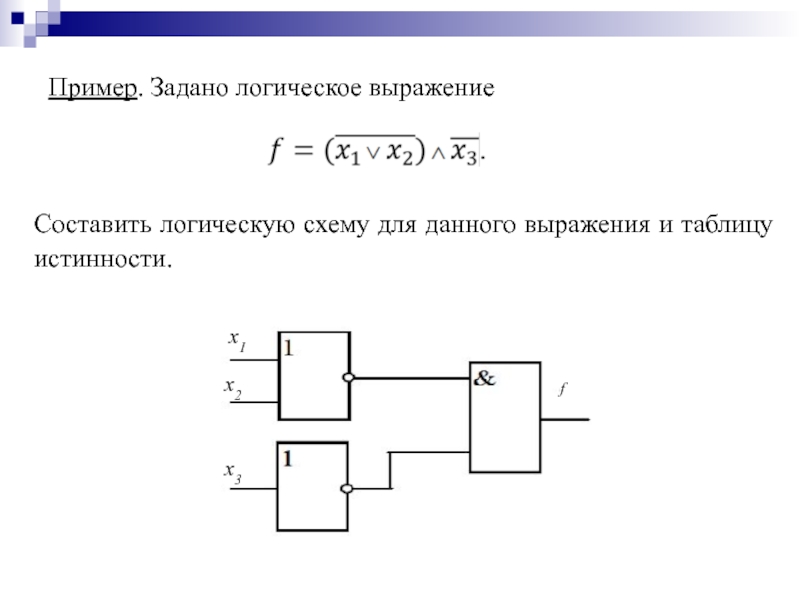
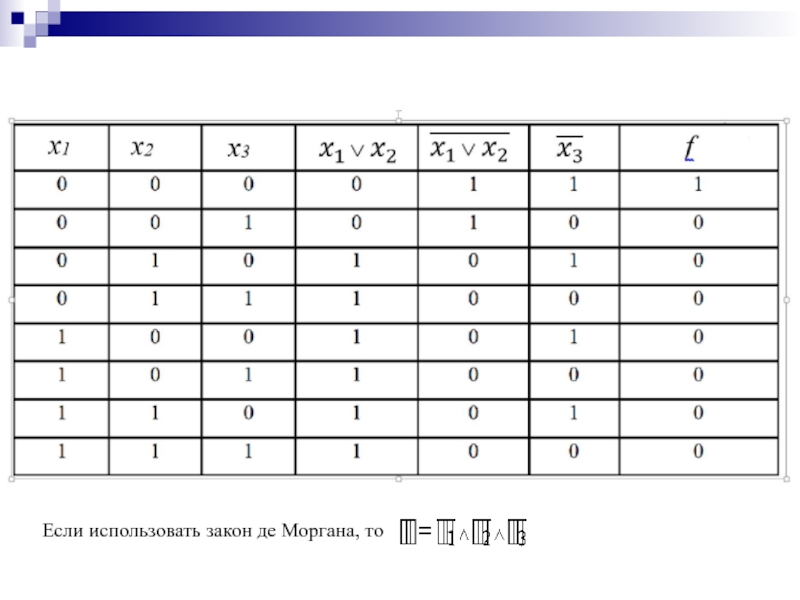
- 23. Пример. Задано логическое выражение Составить логическую схему для данного выражения и таблицу истинности.
- 24. Если использовать закон де Моргана, то
- 25. Элементарной конъюнкцией называется логическое произведение любого конечного
- 26. Дизъюнктивной нормальной формой (ДНФ) логической функции называется
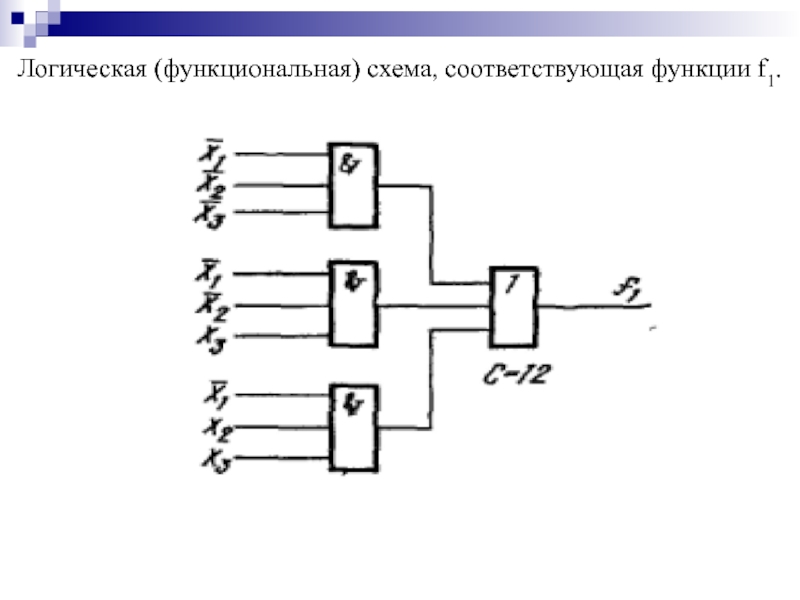
- 27. Логическая (функциональная) схема, соответствующая функции f1.
- 28. Конъюнктивной нормальной формой (КНФ) называется конъюнкция элементарных дизъюнкций. Например Пример СКНФ
- 29. Набор И, ИЛИ, НЕ избыточен, поскольку функцию
- 30. Локальные методы упрощения ДНФ Поглощение определяется формулой
- 31. Импликанты x1x2 и x2x3 являются простыми импликантами
- 32. Алгоритм минимизации Квайна Операция неполного склеивания Пример. Получить сокращенную ДНФ
- 33. Сокращенная ДНФ Таблица импликант
- 34. Метод Квайна-Мак-Класки. Позволяет существенно уменьшить число попарных
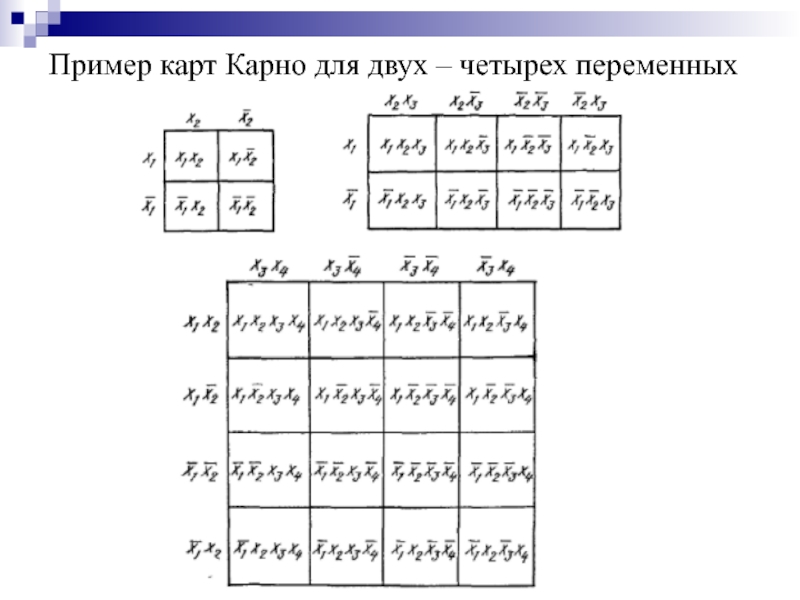
- 35. Пример карт Карно для двух – четырех переменных
- 36. Пример. Минимизировать логическую функцию Приведем к ДНФ Приведем к СДНФ
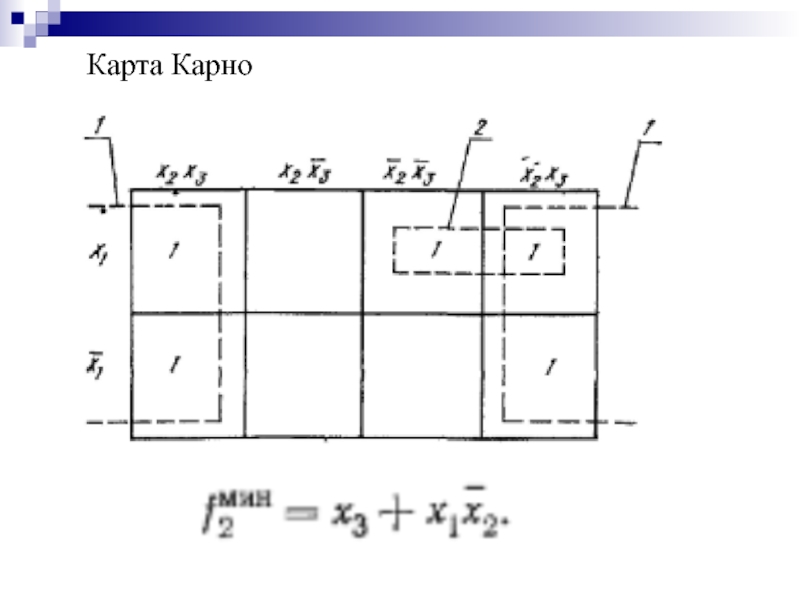
- 37. Карта Карно
- 38. Минимизация не полностью определенных логических функций Минимизировать логическую функцию имеющую два запрещенных набора f=
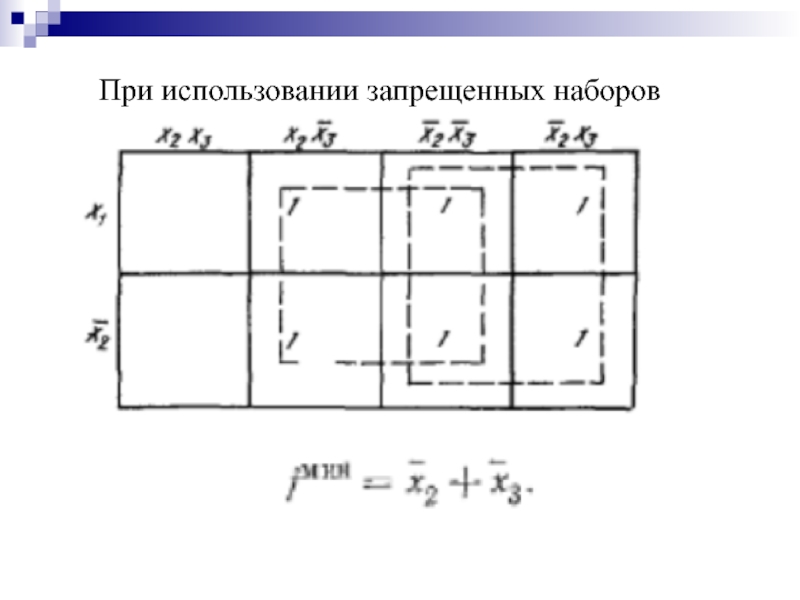
- 39. При использовании запрещенных наборов
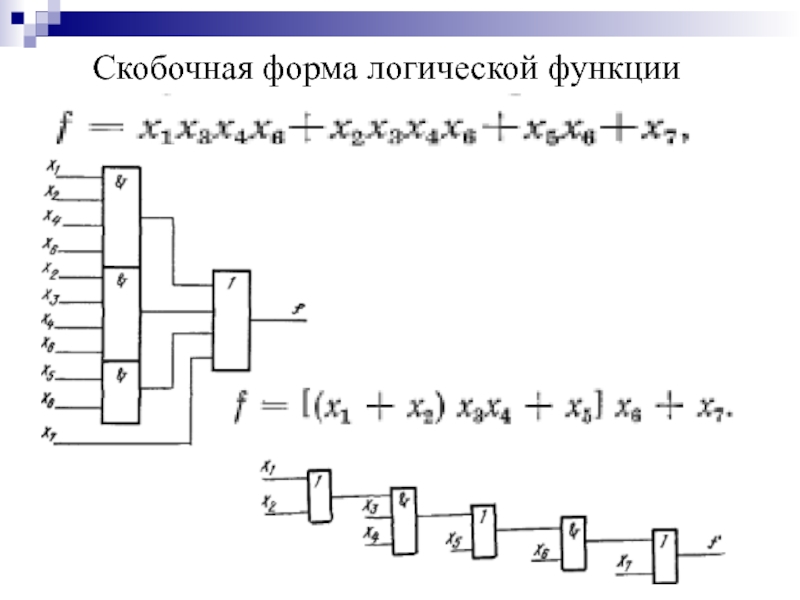
- 40. Скобочная форма логической функции
- 41. Формы представления чисел в ЭВМ и их
- 42. В случае правильных дробей минимальным по модулю
- 43. Представление чисел с плавающей запятой В общем
- 44. Нормализованные числа – числа для которых выполняется соотношение 1/r ≤ |M|
- 45. Наименьшее по модулю число с плавающей запятой
- 46. Сравним диапазон представления чисел с фиксированной и
- 47. Погрешности представления чисел Для чисел с фиксированной
- 48. При использовании округления максимальная абсолютная ошибка не
- 49. Для минимального значения: Погрешности представления чисел откуда
- 50. Для нахождения погрешностей представления чисел в форме
- 51. Прямой код. Правило образования прямого кода
- 52. Правило образования прямого кода правильной дроби записывается
- 53. Дополнительный код. В основе дополнительного кода n-разрядного
- 54. Дополнительный код. Пример. Записать дополнительный код
- 55. Дополнительный код отрицательной n-разрядной правильной дроби A
- 56. Обратный код. В основе обратного кода n-разрядного
- 57. Обратный код отрицательной n-разрядной правильной дроби A
- 58. Двоично-кодированное представление десятичных чисел Наиболее часто используется
- 59. При образовании Д-кода следует исходить из общих
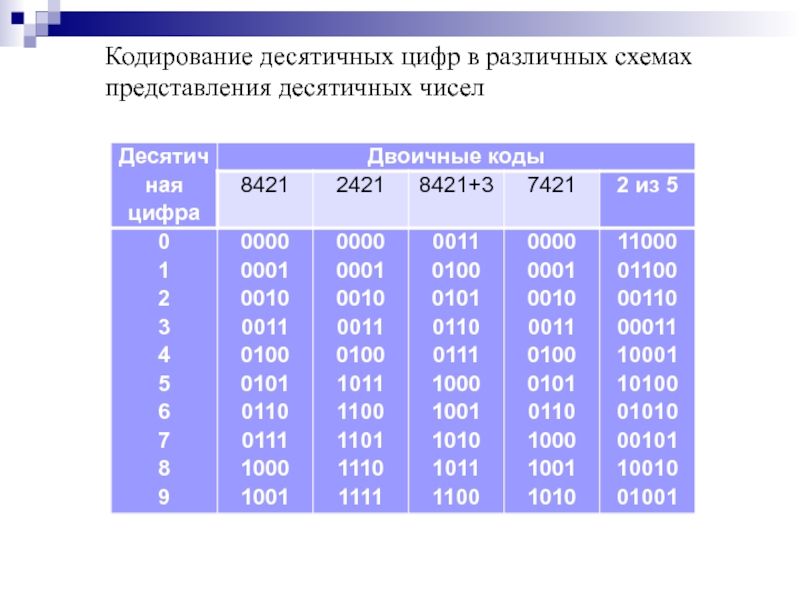
- 60. Кодирование десятичных цифр в различных схемах представления десятичных чисел
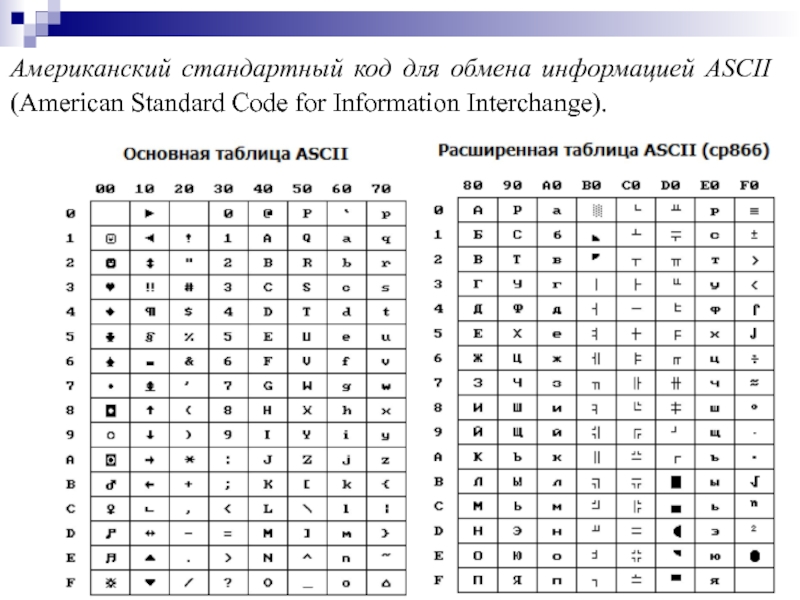
- 61. Американский стандартный код для обмена информацией ASCII (American Standard Code for Information Interchange).
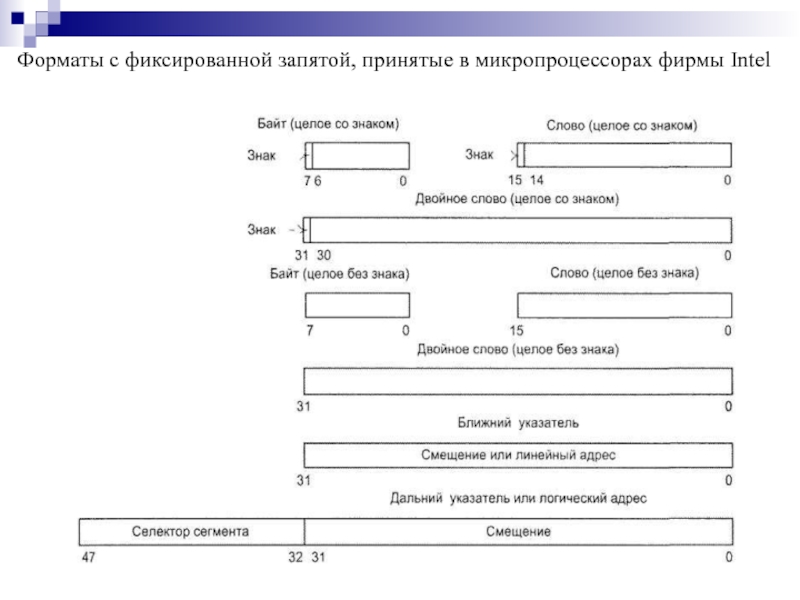
- 62. Форматы с фиксированной запятой, принятые в микропроцессорах фирмы Intel
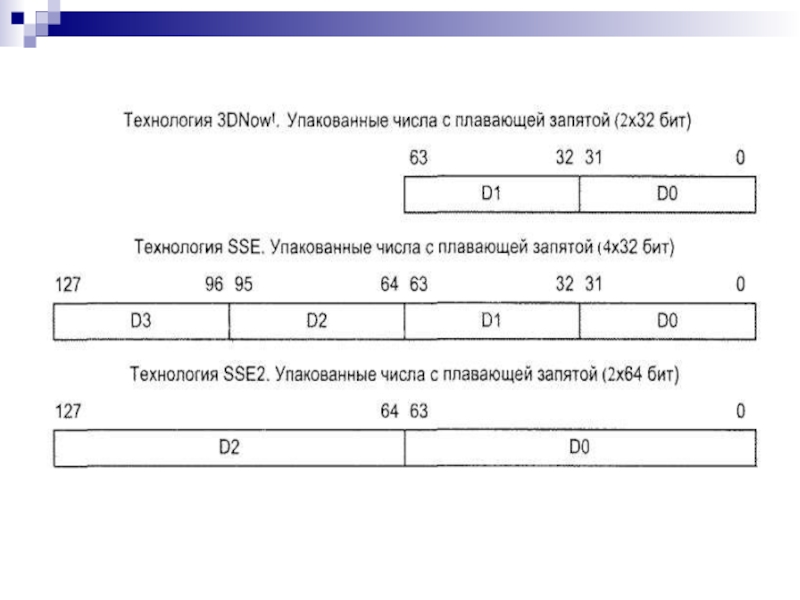
- 63. Упакованные целые числа Десятичные числа
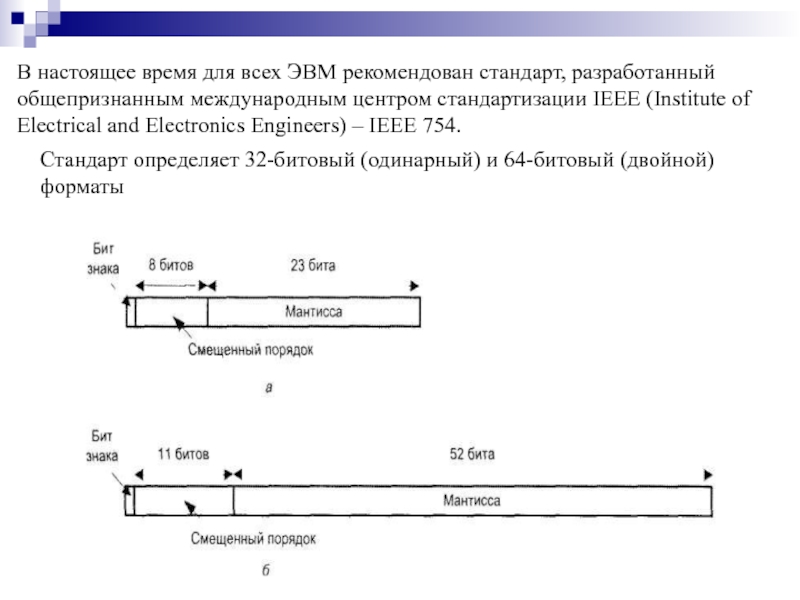
- 64. В настоящее время для всех ЭВМ рекомендован
- 66. Двоичная арифметика с фиксированной запятой Правила выполнения
- 67. Правила поразрядных действий при сложении двух двоичных
- 68. Правила поразрядных действий при вычитании двух двоичных
- 69. Пример. Сложить два числа в прямых кодах:
- 70. Сумма дополнительных кодов чисел есть дополнительный код
- 71. Сумма обратных кодов чисел есть обратный код суммы чисел.
- 72. Пример. Сложить два числа в обратных кодах:
- 73. Пример. Сложить два отрицательных числа в дополнительных
- 74. Пример. Записать в модифицированном коде: а) положительное
- 75. Пример. Сложить два отрицательных числа в модифицированных
- 76. Умножение, начиная с младших разрядов множителя, при
- 77. Умножение, начиная со старших разрядов множителя, при
- 78. Умножение, начиная со старших разрядов множителя, со
- 79. Умножение, начиная с младших разрядов множителя, со
- 80. Пример. Умножить по второму методу два целых
- 81. Пример. Умножить по четвертому методу два целых
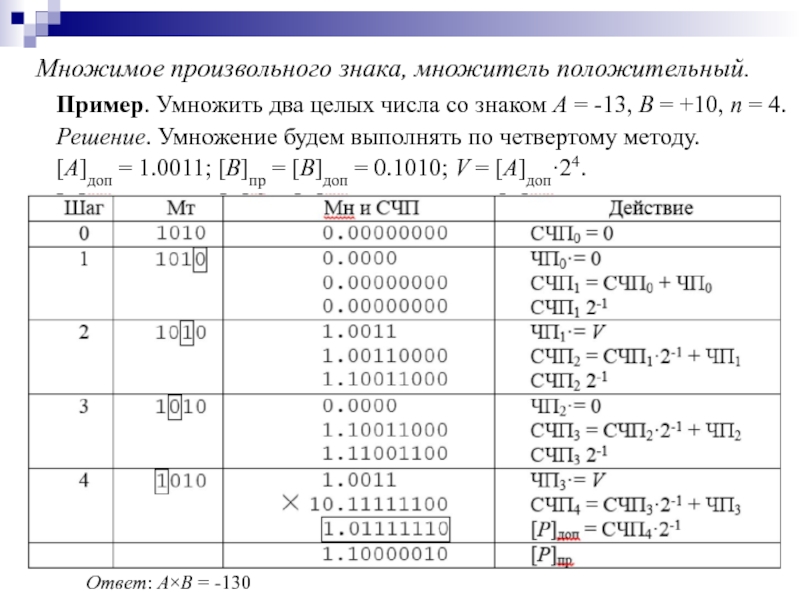
- 82. Множимое произвольного знака, множитель положительный. Пример. Умножить
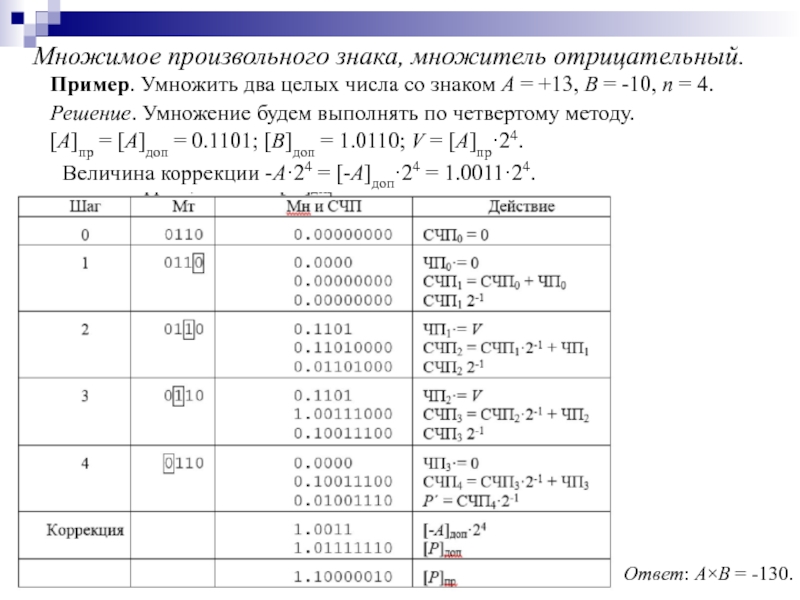
- 83. Множимое произвольного знака, множитель отрицательный. Пример. Умножить
- 84. Алгоритм Бута. В основе алгоритма Бута
- 85. Реализация алгоритма предполагает последовательный в направлении справа
- 86. Пример. Умножить два целых числа без знака
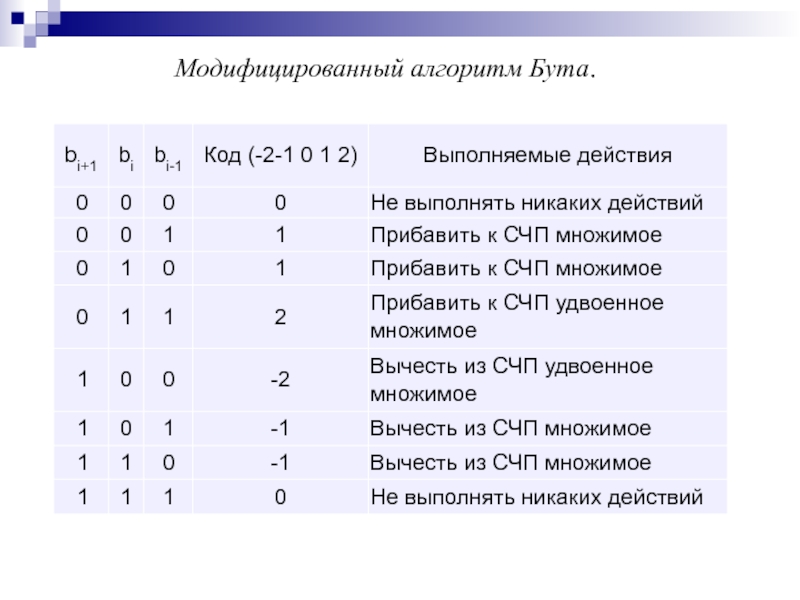
- 87. Модифицированный алгоритм Бута.
- 88. Пример. Умножить два целых числа со знаком
- 89. Деление чисел с фиксированной запятой Задача сводится
- 90. Деление с восстановлением остатка и неподвижным делителем
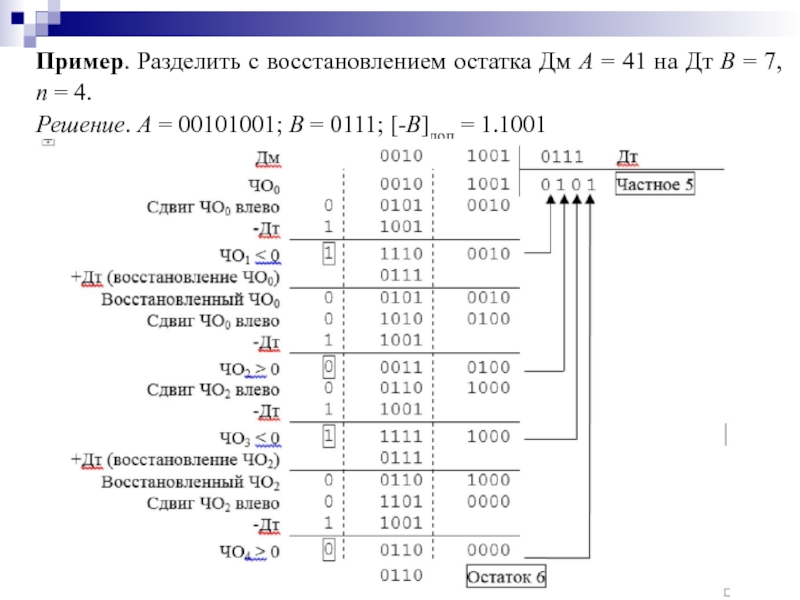
- 91. Пример. Разделить с восстановлением остатка Дм A
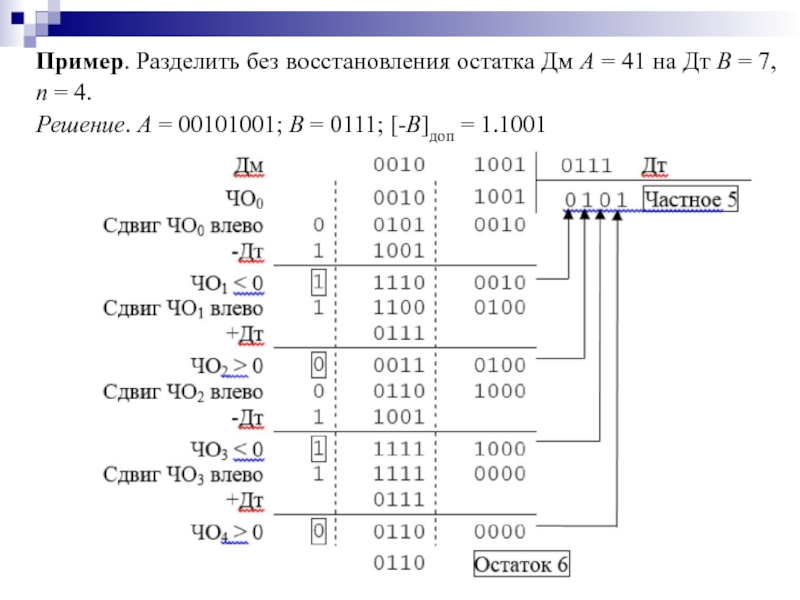
- 92. Пример. Разделить без восстановления остатка Дм A
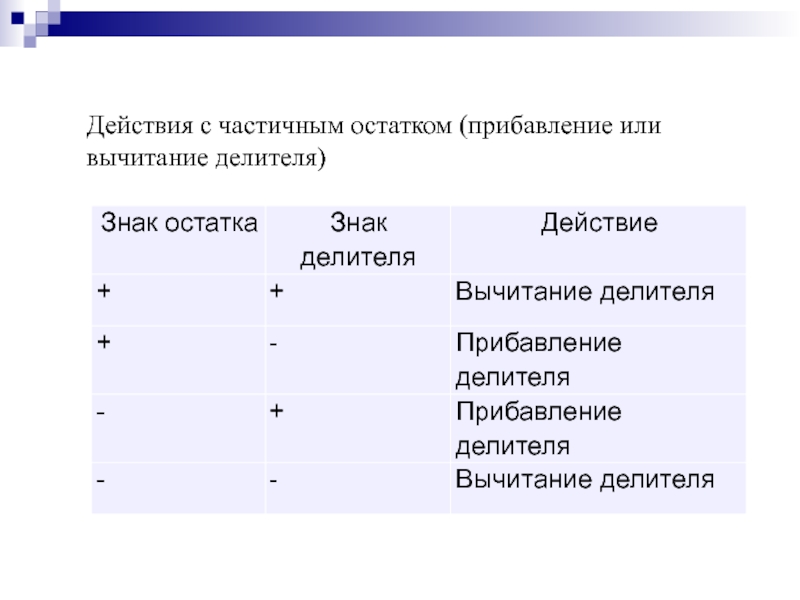
- 93. Действия с частичным остатком (прибавление или вычитание делителя)
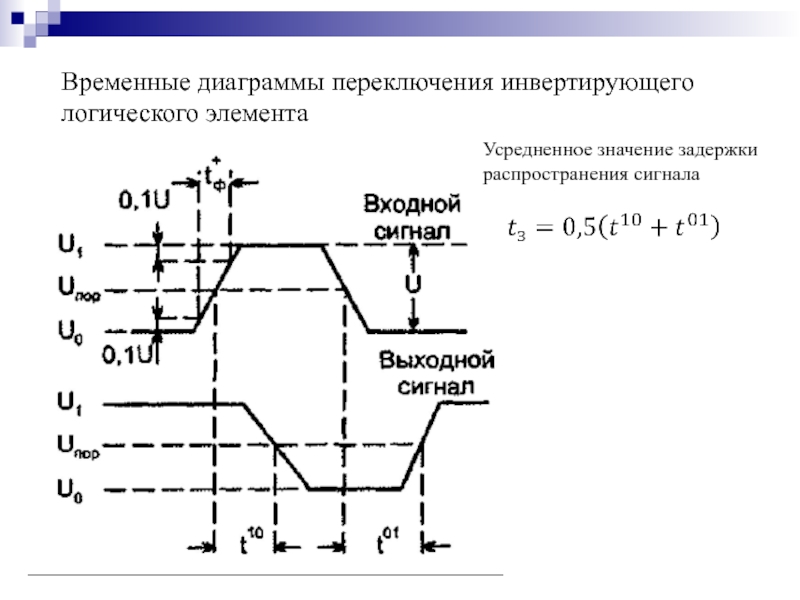
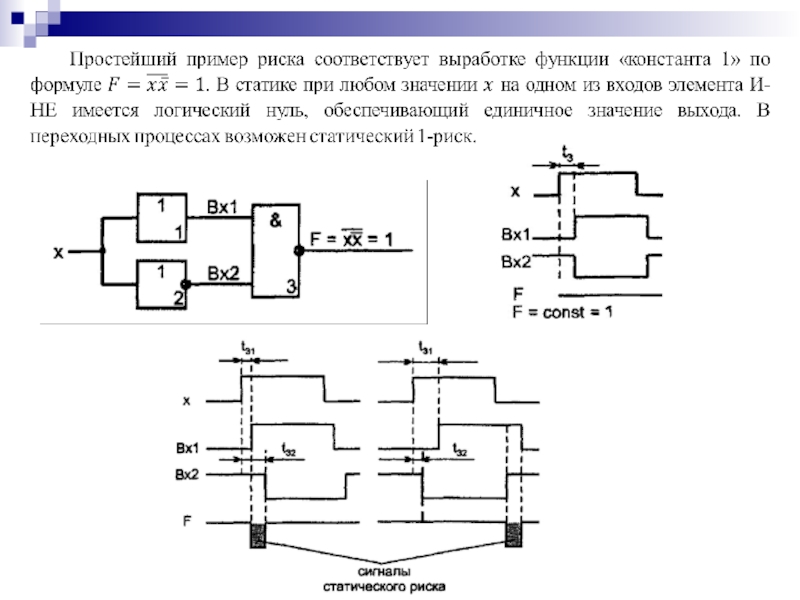
- 94. Временные диаграммы переключения инвертирующего логического элемента Усредненное значение задержки распространения сигнала
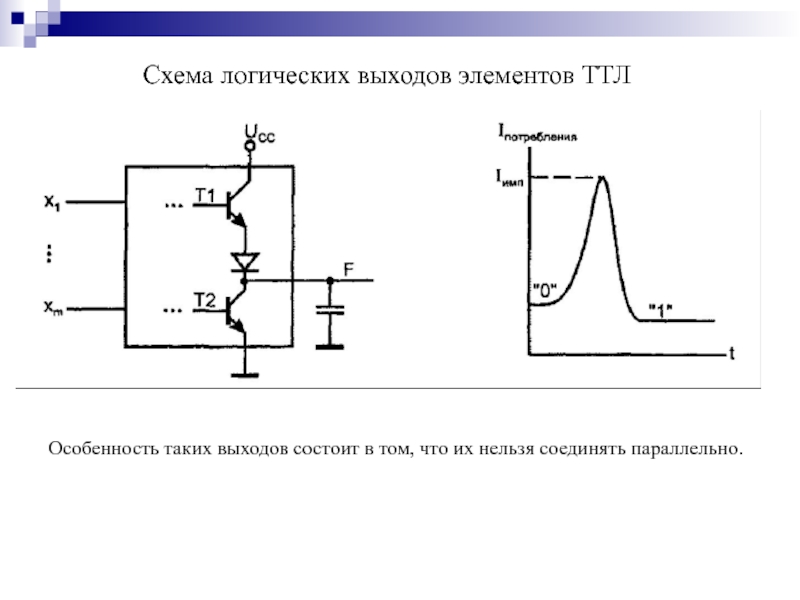
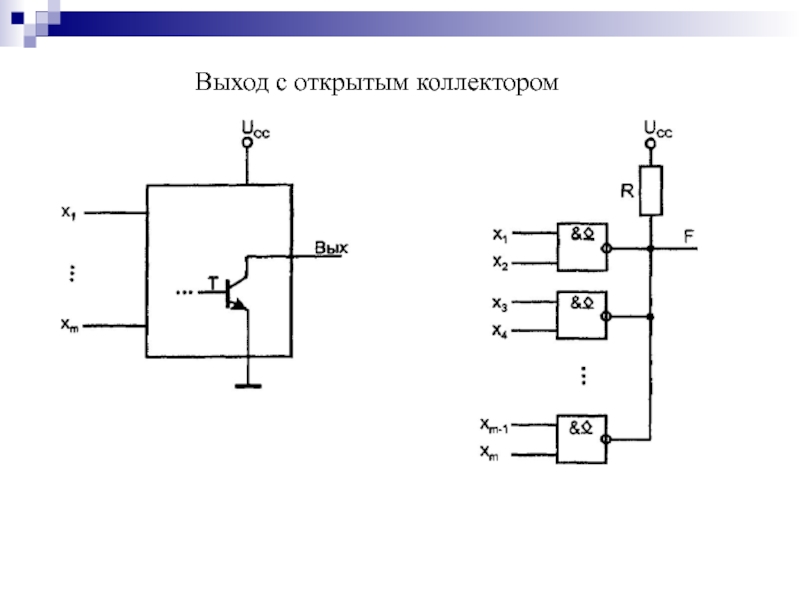
- 95. Схема логических выходов элементов ТТЛ Особенность таких
- 96. Выход с открытым коллектором
- 97.
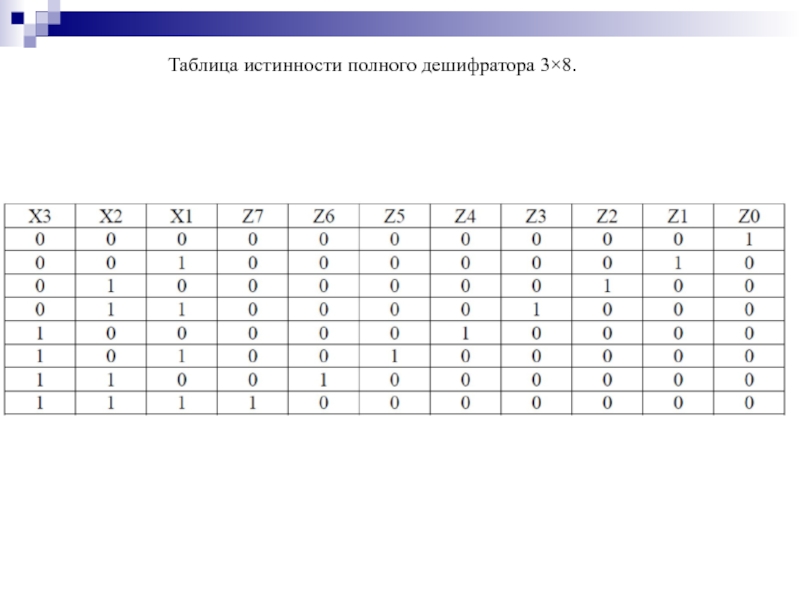
- 98. Таблица истинности полного дешифратора 3×8.
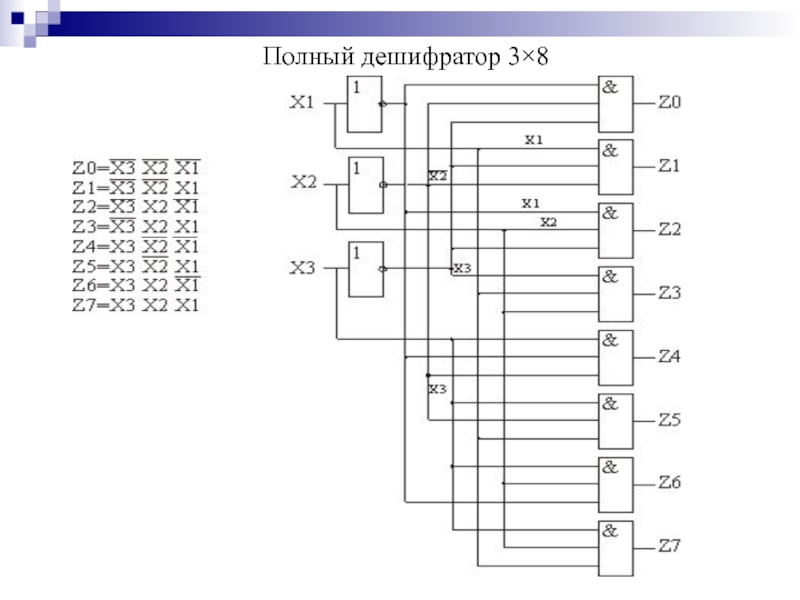
- 99. Полный дешифратор 3×8
- 100. Функционирование дешифратора описывается системой конъюнкций: При ЕN
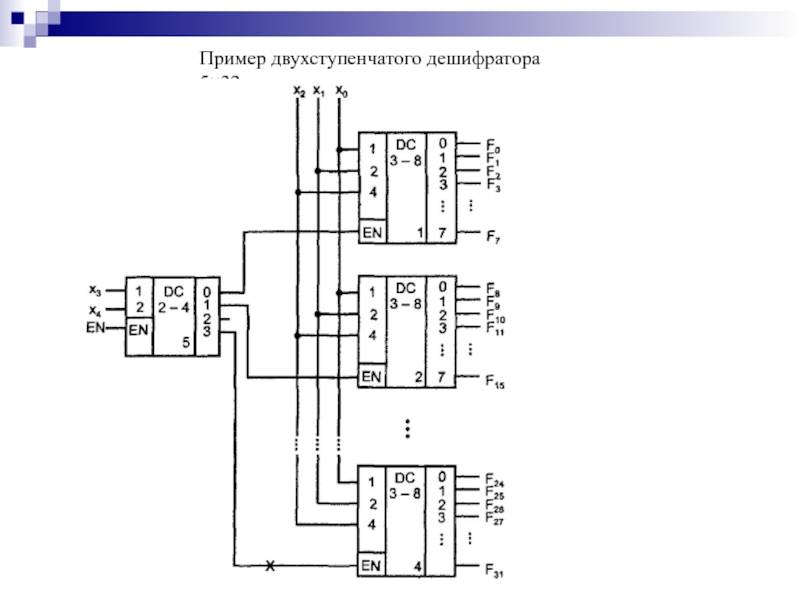
- 101. Пример двухступенчатого дешифратора 5×32
- 102. Приоритетный шифратор для восьмиразрядных слов.
- 103. можно упростить их и получить выражения
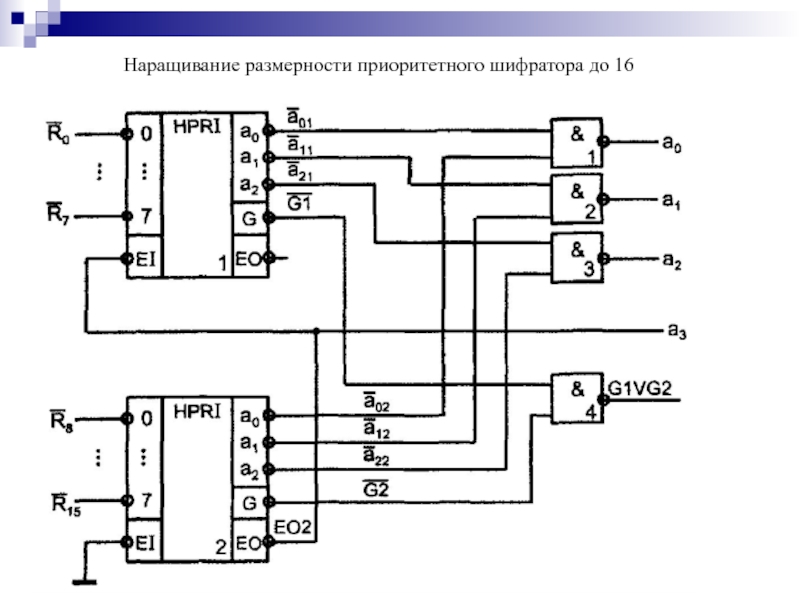
- 104. Наращивание размерности приоритетного шифратора до 16
- 105. Мультиплексор Двоичный код, поступающий на адресные входы,
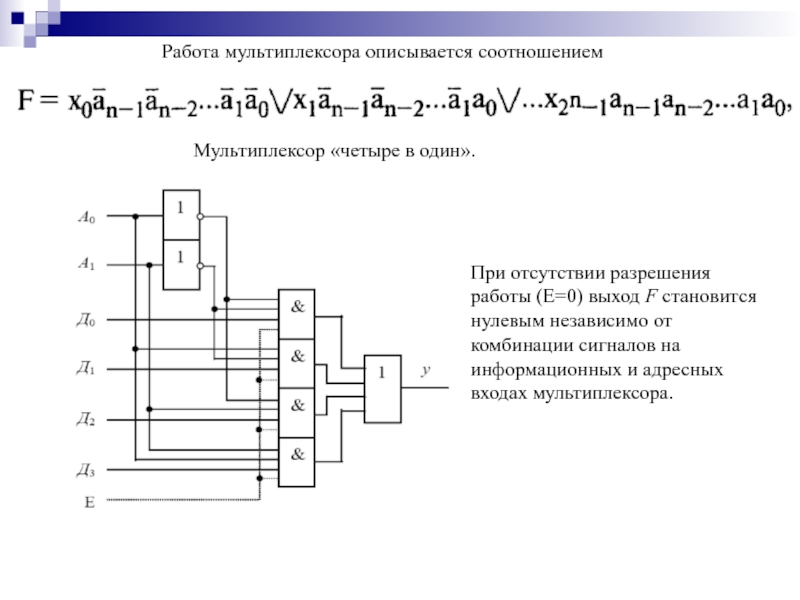
- 106. Работа мультиплексора описывается соотношением Мультиплексор «четыре
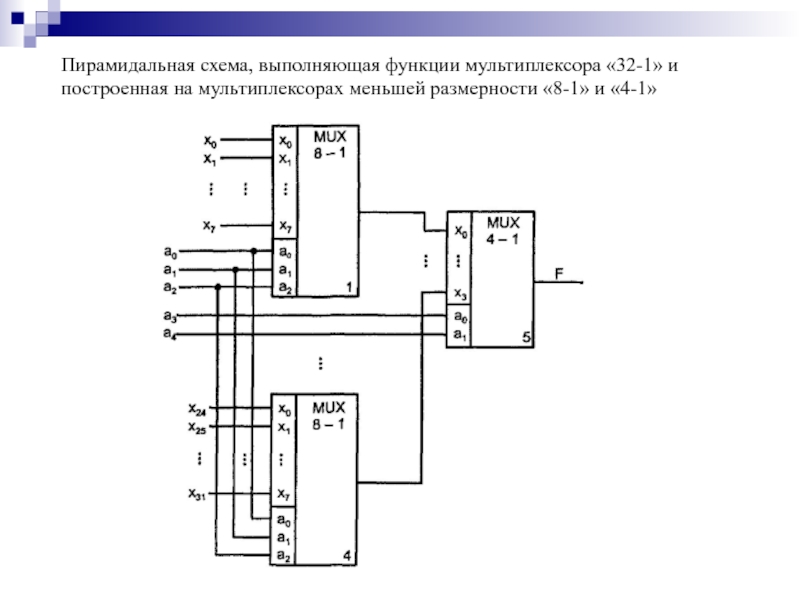
- 107. Пирамидальная схема, выполняющая функции мультиплексора «32-1» и построенная на мультиплексорах меньшей размерности «8-1» и «4-1»
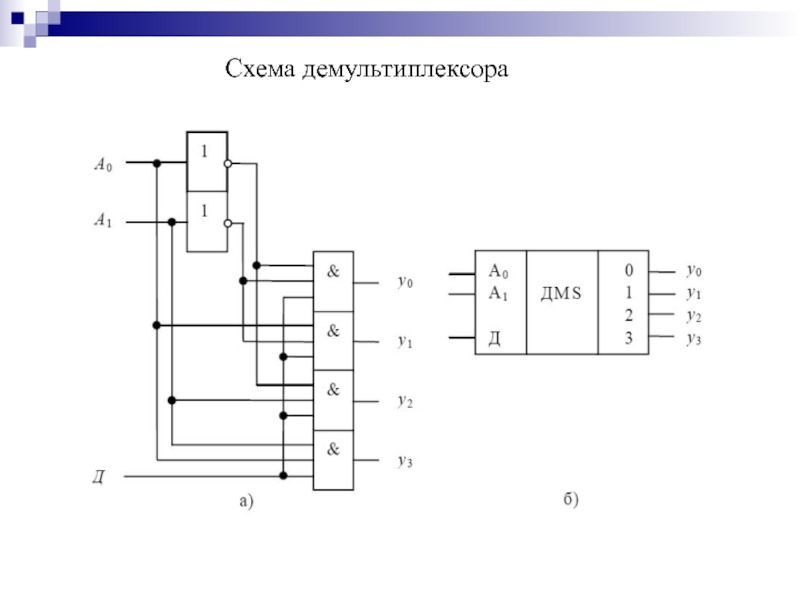
- 108. Демультиплексор Функционирование демультиплексора, имеющего n =
- 109. Схема демультиплексора
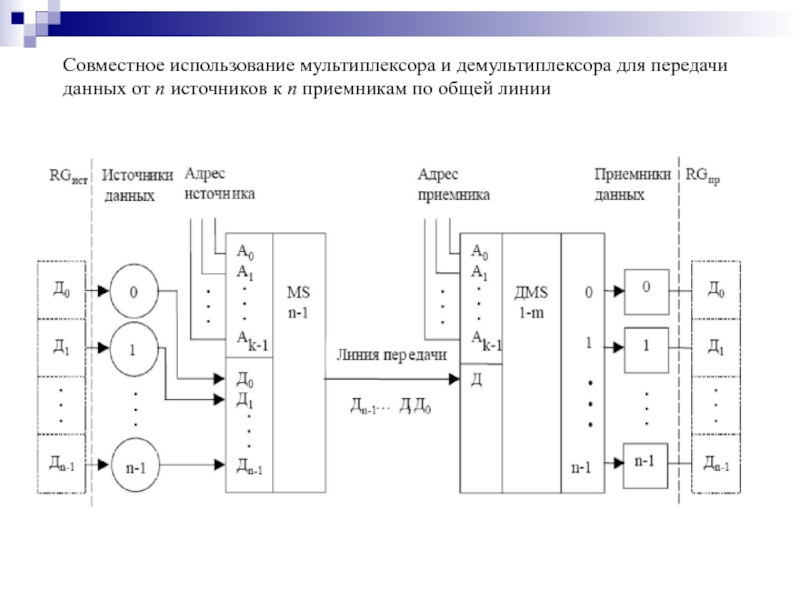
- 110. Совместное использование мультиплексора и демультиплексора для передачи
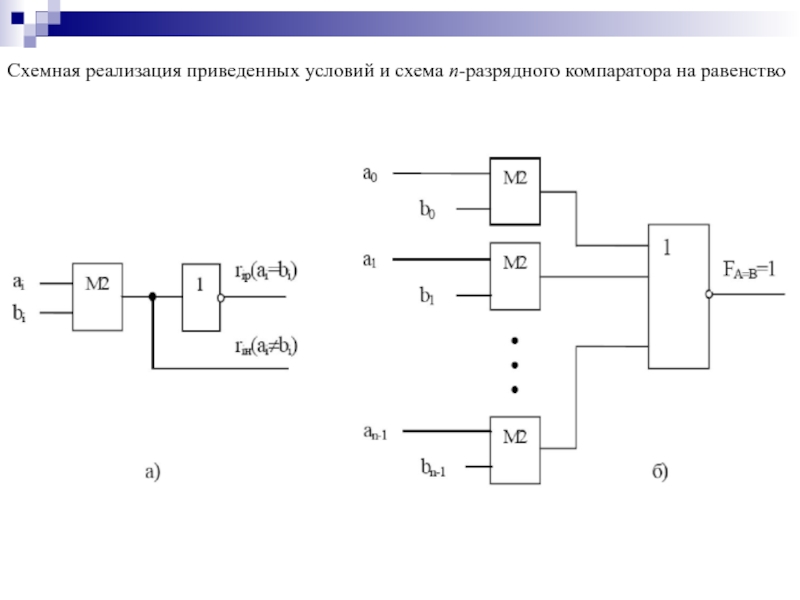
- 111. Функции, вырабатываемые компараторами, определяются следующим образом: они
- 112. Схемная реализация приведенных условий и схема n-разрядного компаратора на равенство
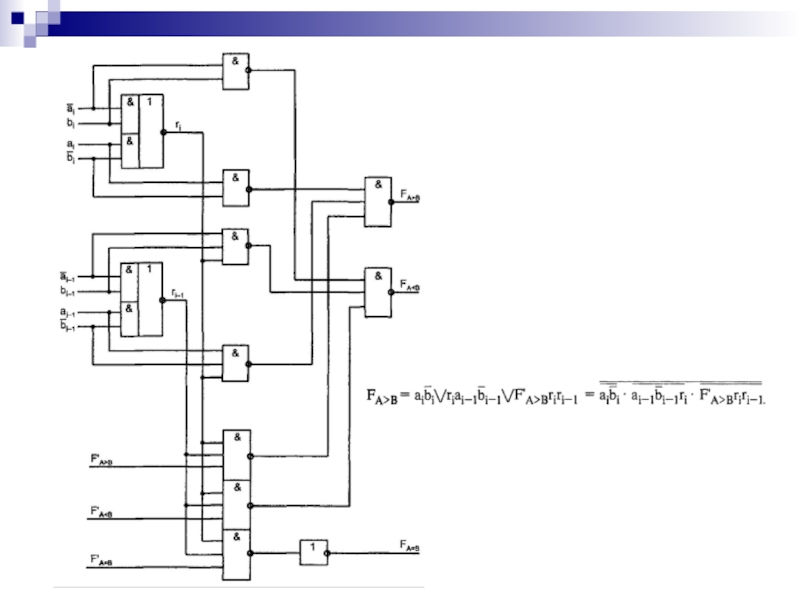
- 113. Для общего случая n-разрядных слов
- 115. Сумматоры Сумматор – операционный узел, выполняющий арифметическое
- 116. Полный одноразрядный двоичный сумматор имеет три входа:
- 117. Уравнения можно преобразовать следующим образом Выражение для
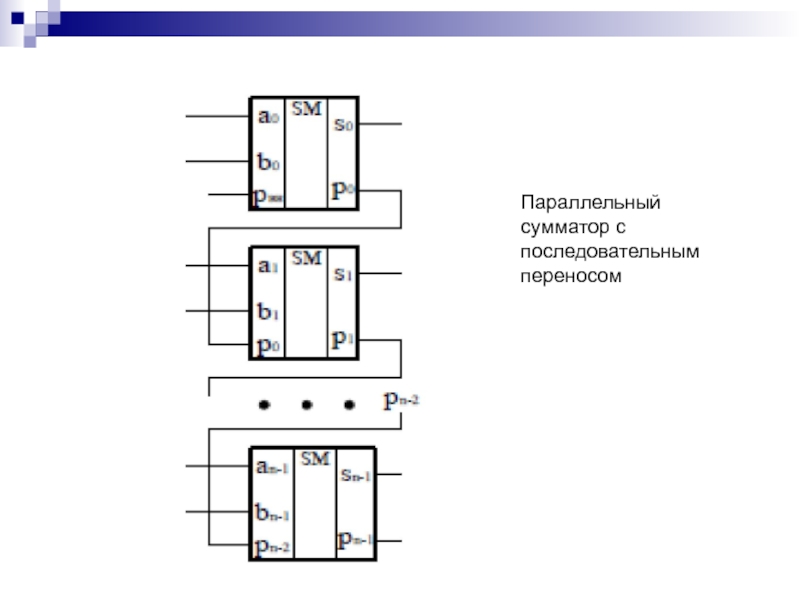
- 118. Параллельный сумматор с последовательным переносом
- 119. Паралельный перенос в i - том разряде
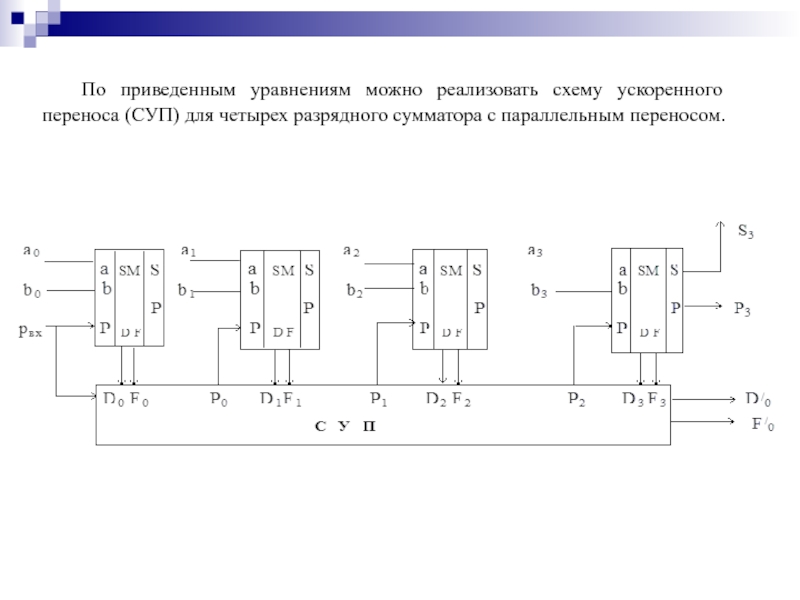
- 120. По приведенным уравнениям можно реализовать схему ускоренного
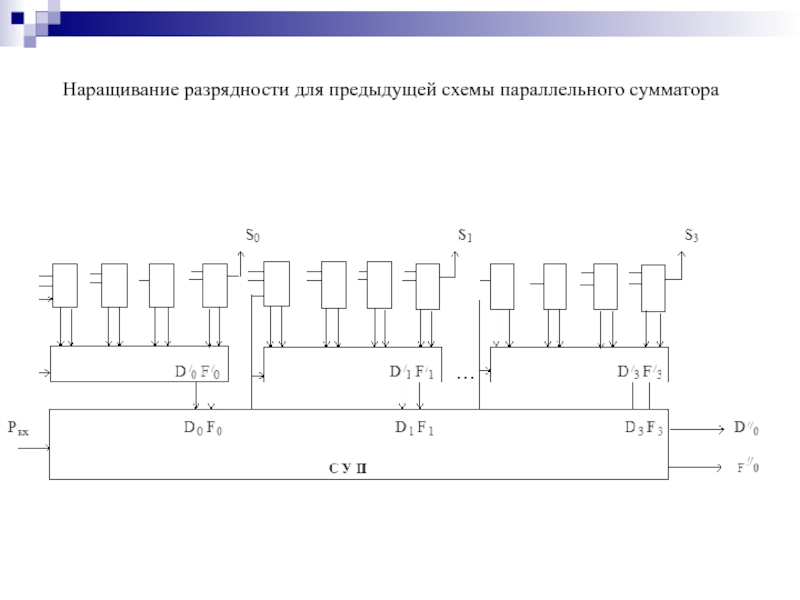
- 121. Наращивание разрядности для предыдущей схемы параллельного сумматора
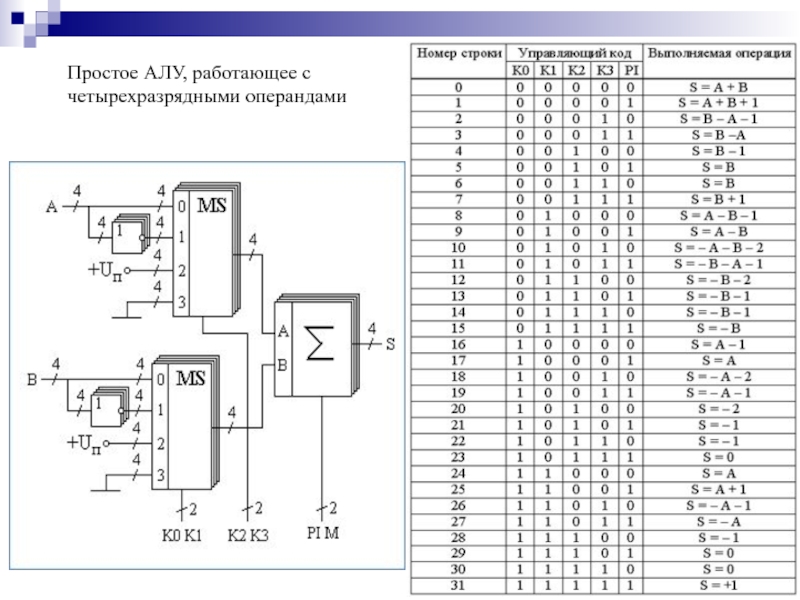
- 122. Простое АЛУ, работающее с четырехразрядными операндами
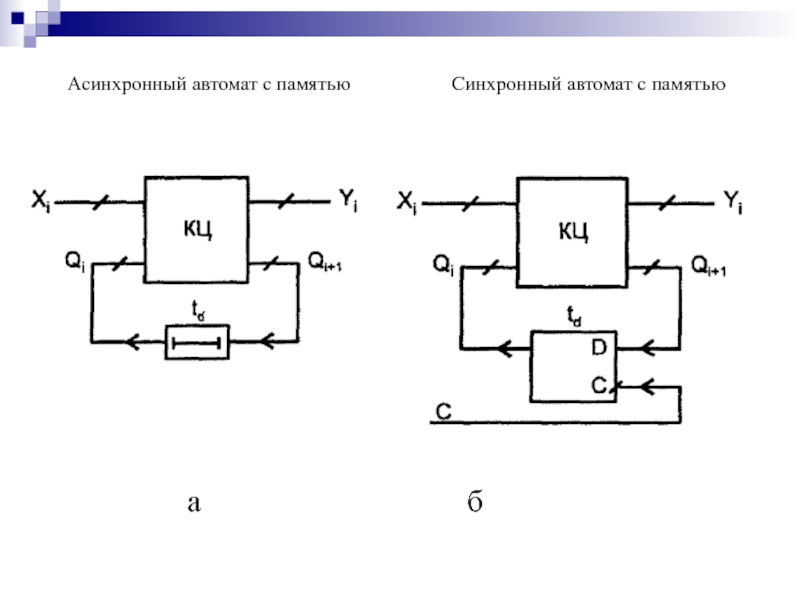
- 123. Синхронный автомат с памятью Асинхронный автомат
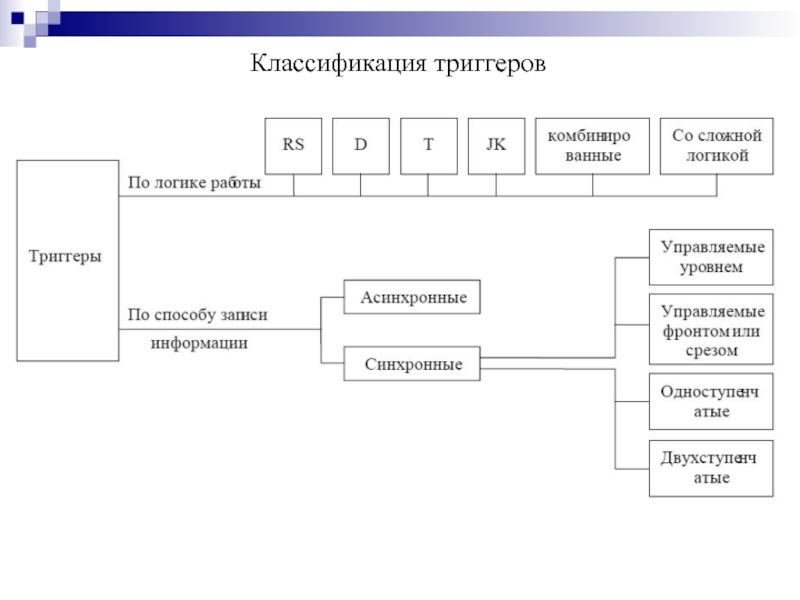
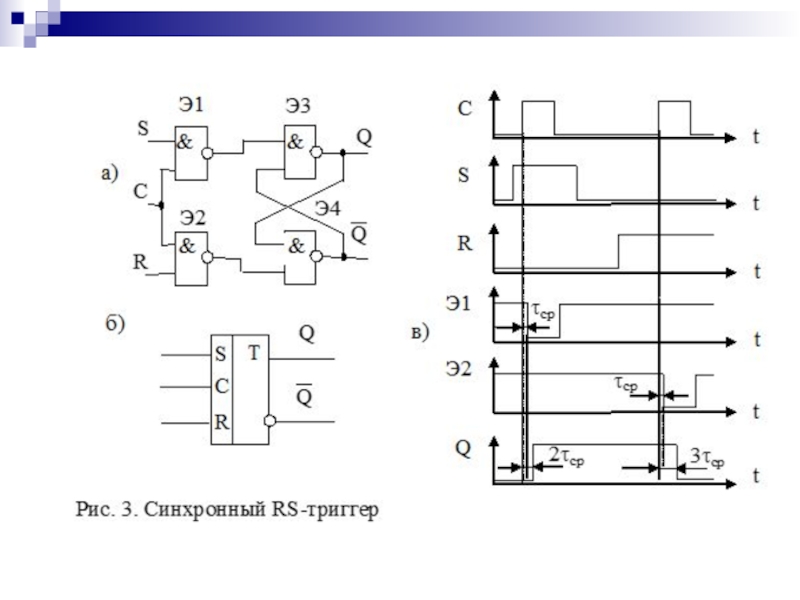
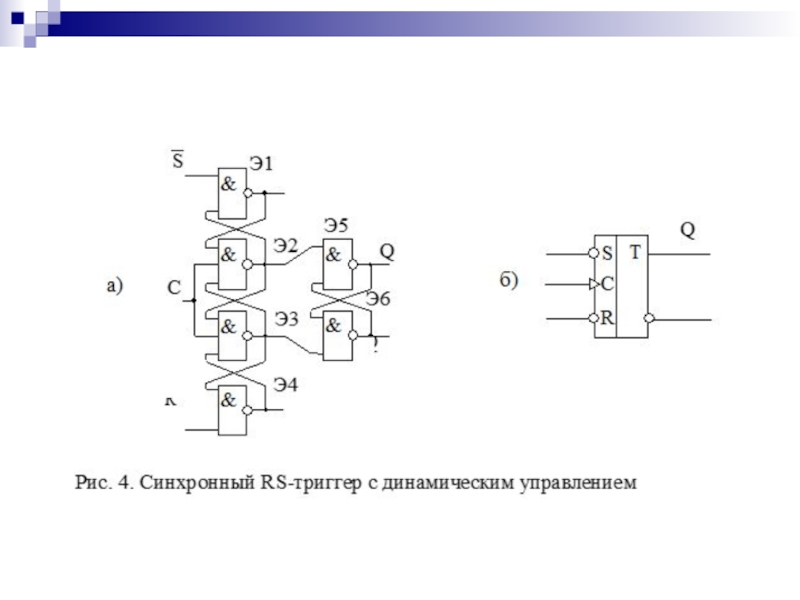
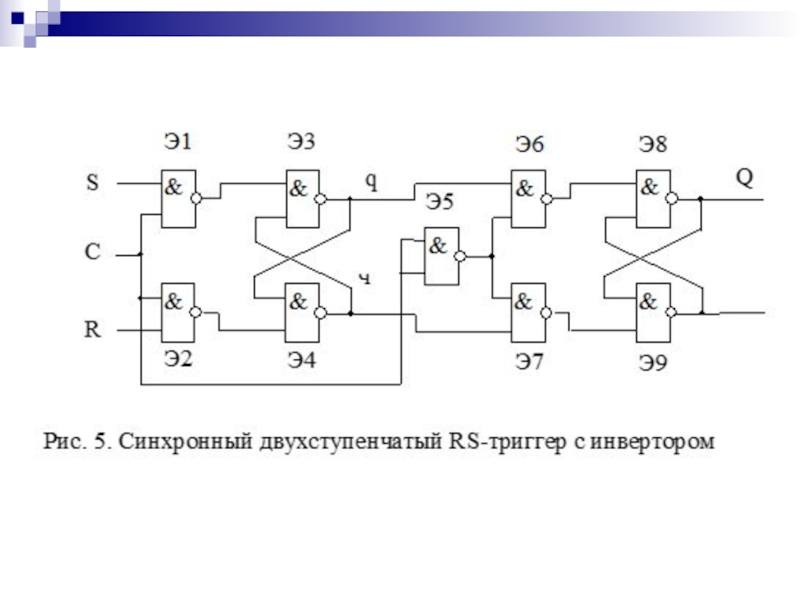
- 124. Классификация триггеров
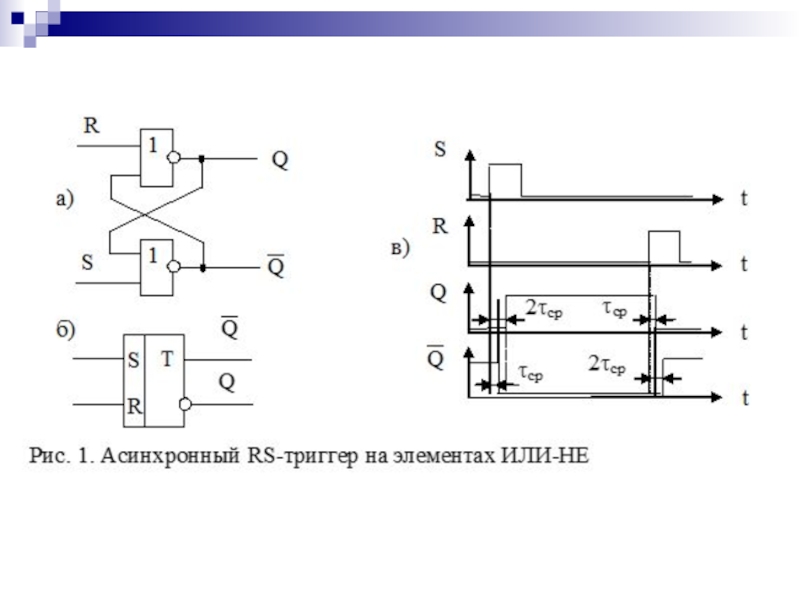
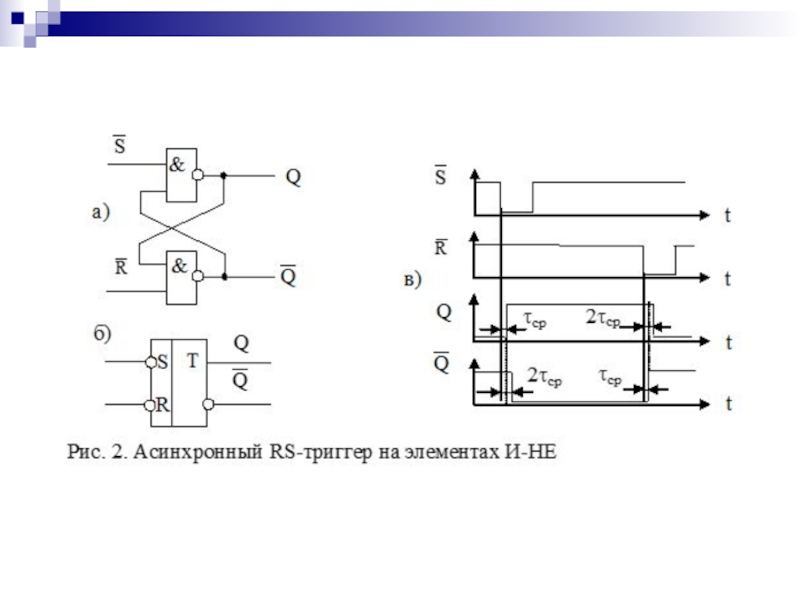
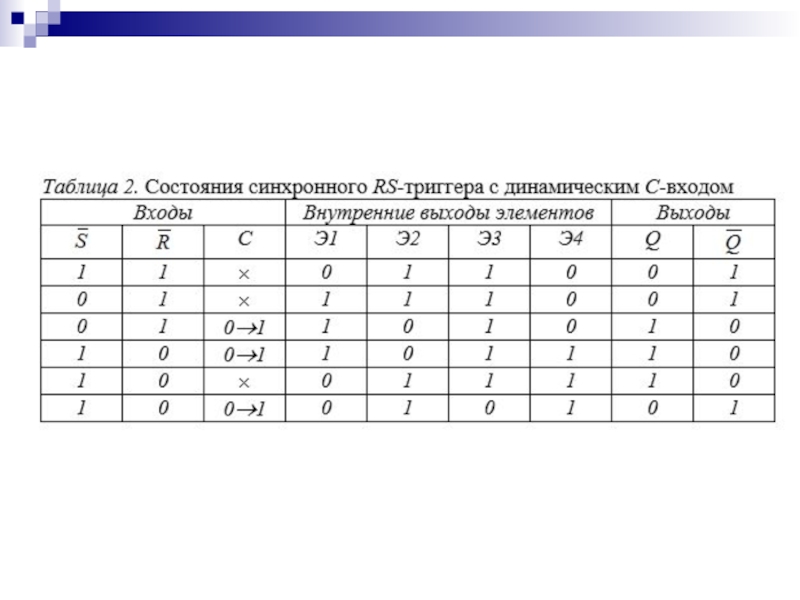
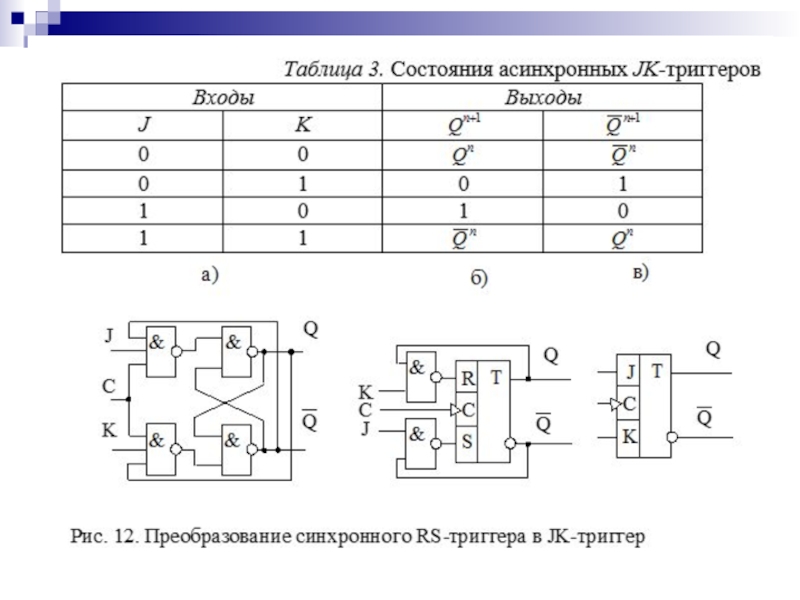
- 125. Таблица переходов асинхронного RS-триггера
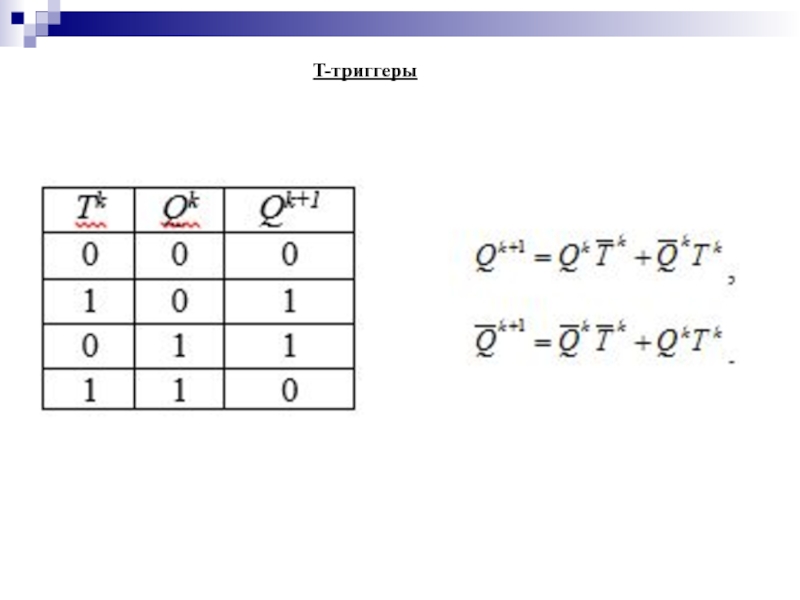
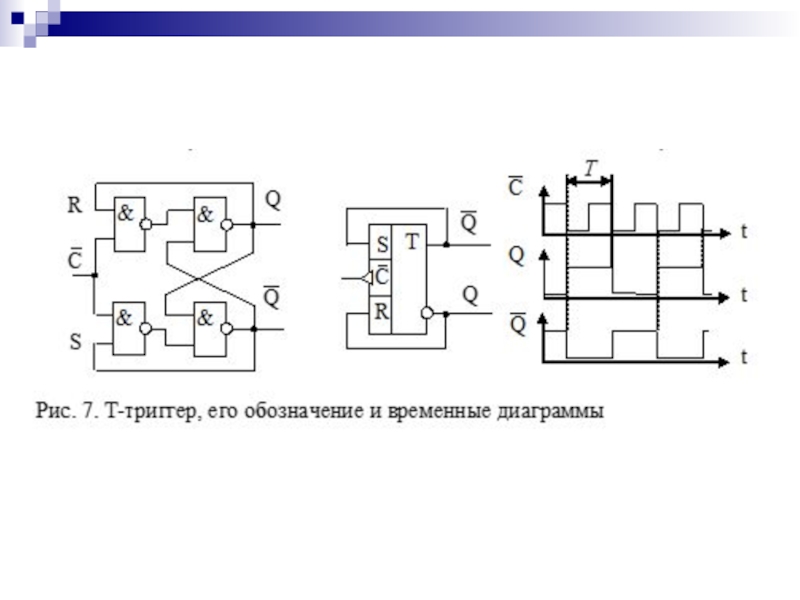
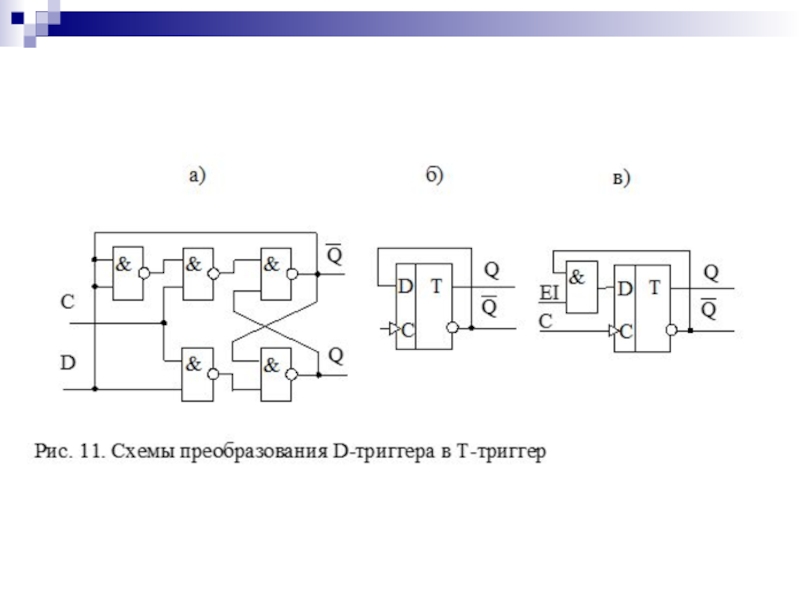
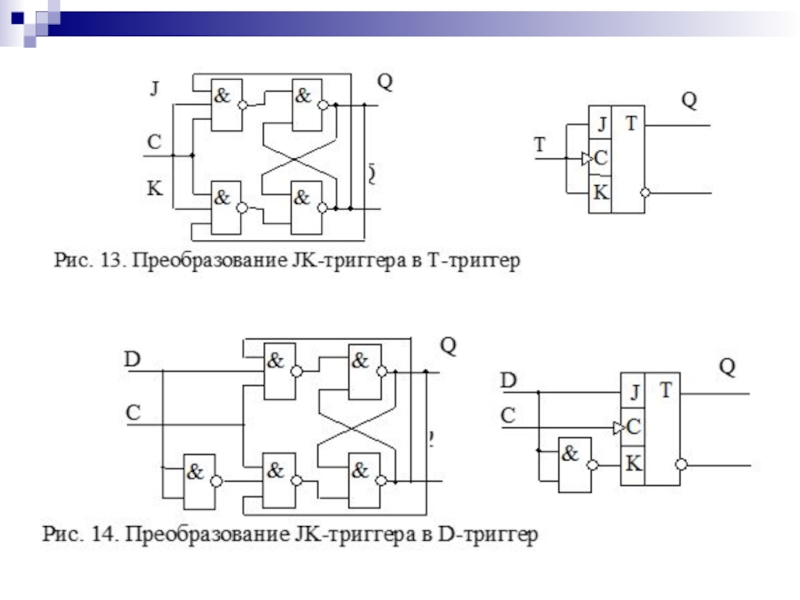
- 132. T-триггеры
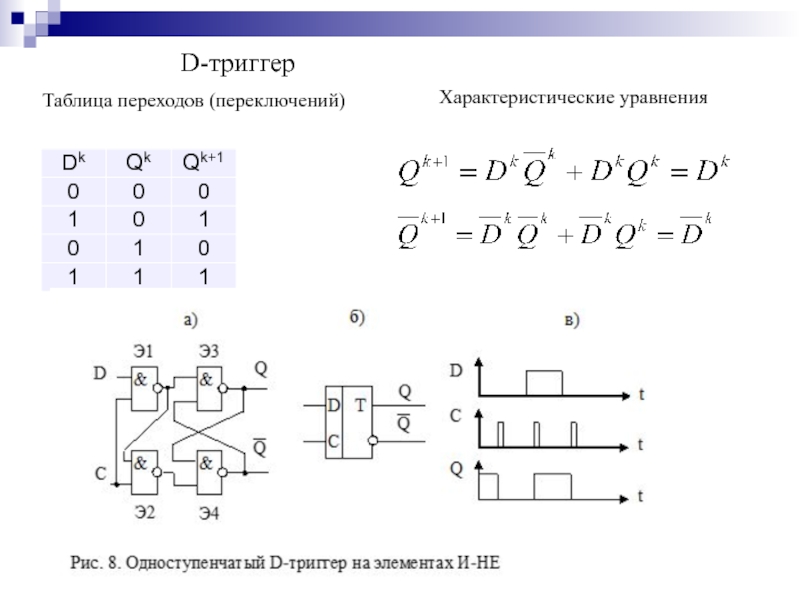
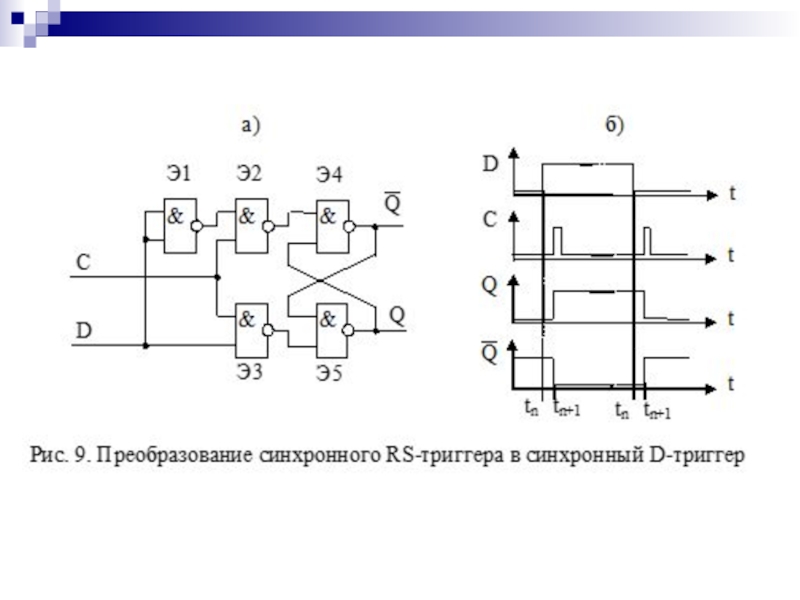
- 134. D-триггер Таблица переходов (переключений) Характеристические уравнения
- 139.
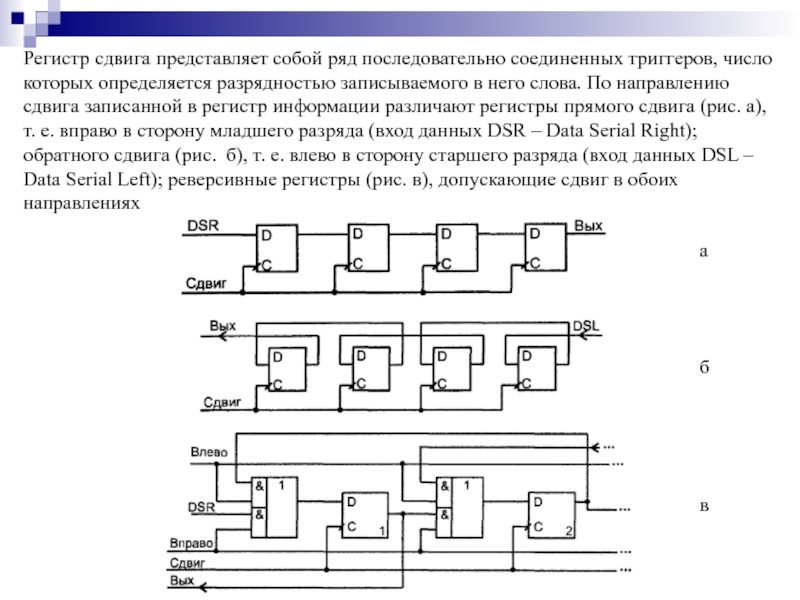
- 140. Регистр сдвига представляет собой ряд последовательно соединенных
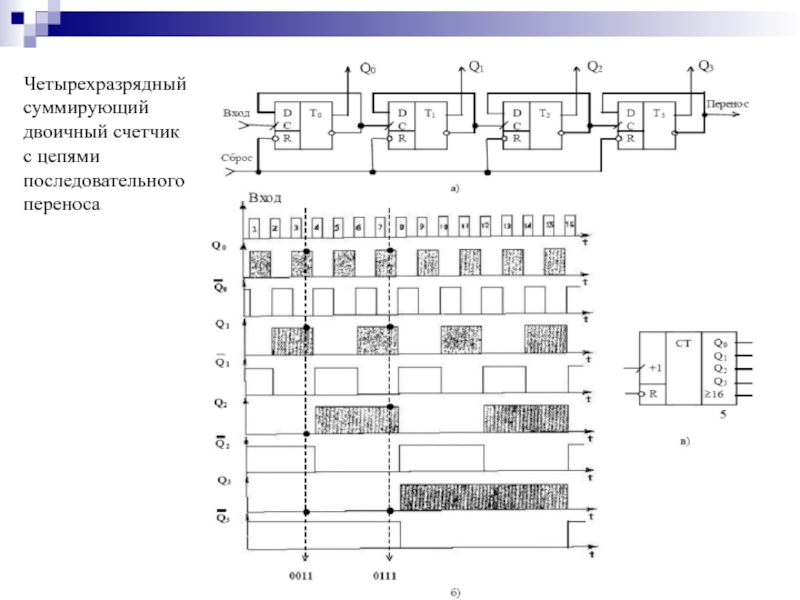
- 141. Четырехразрядный суммирующий двоичный счетчик с цепями последовательного переноса
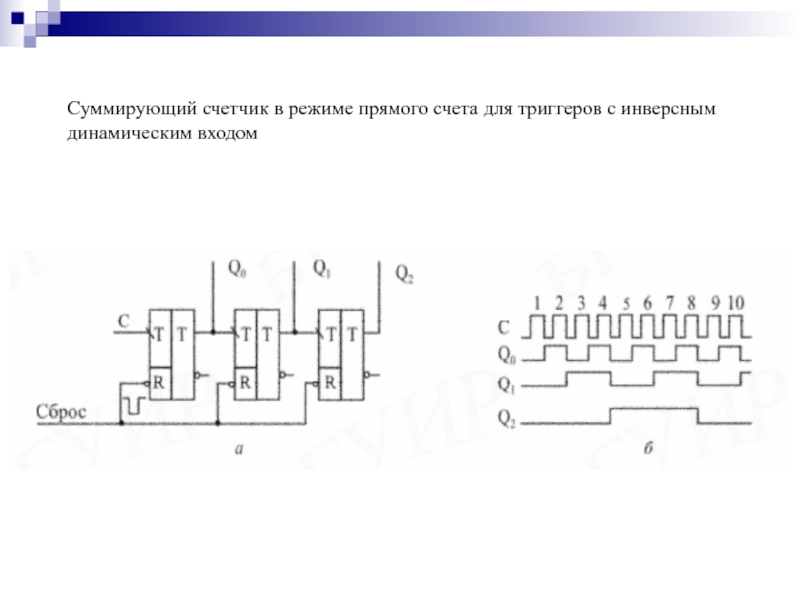
- 142. Суммирующий счетчик в режиме прямого счета для триггеров с инверсным динамическим входом
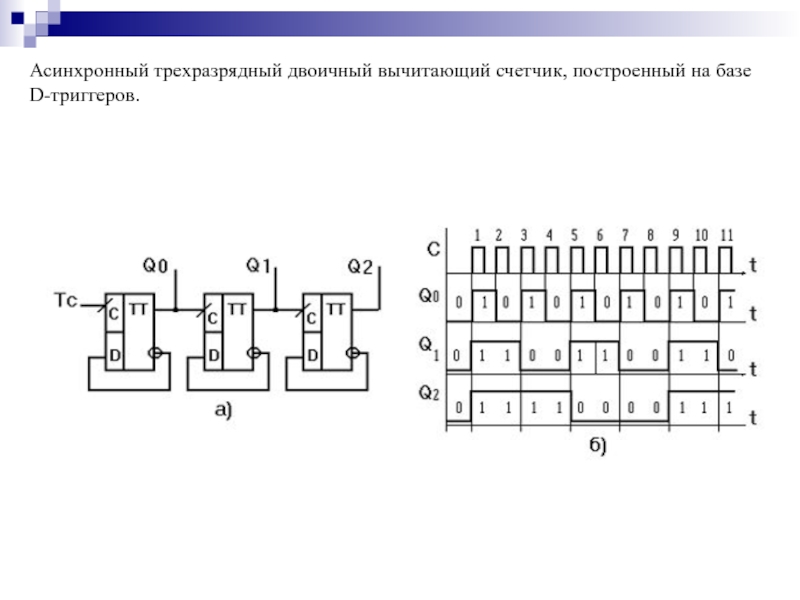
- 143. Асинхронный трехразрядный двоичный вычитающий счетчик, построенный на базе D-триггеров.
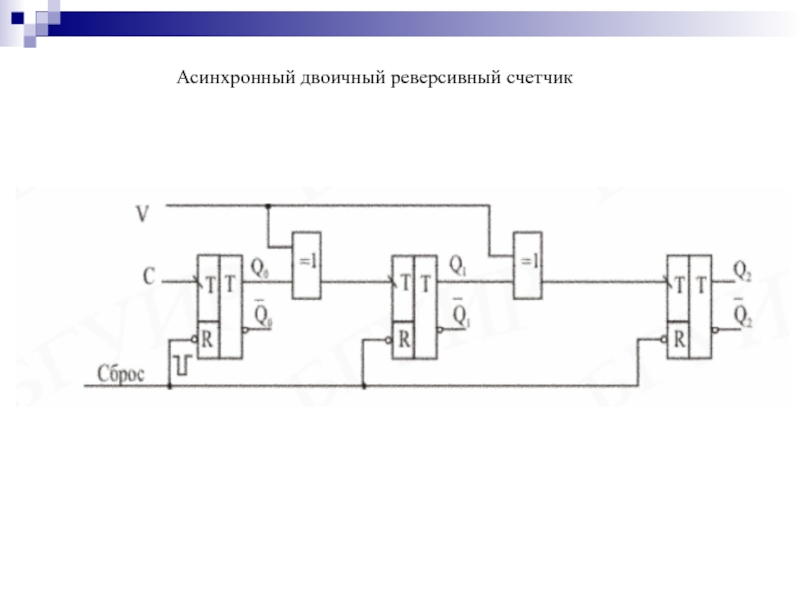
- 144. Асинхронный двоичный реверсивный счетчик
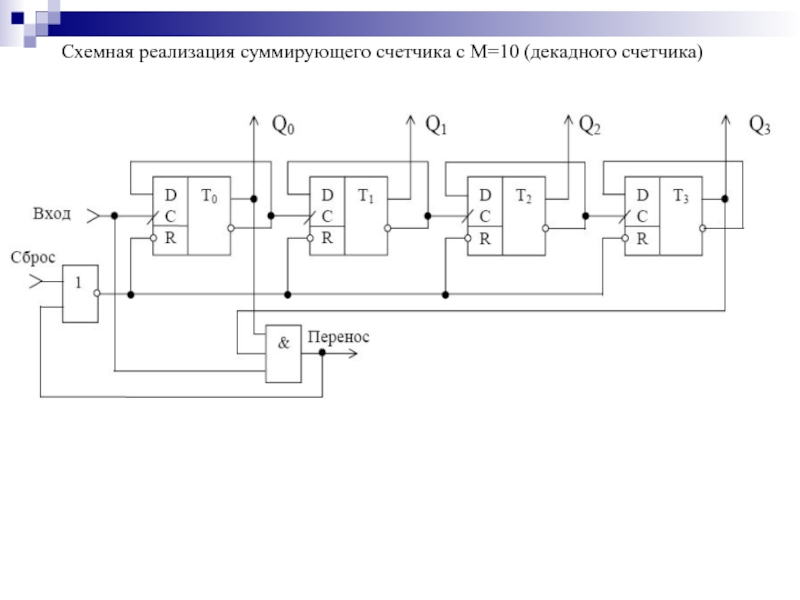
- 145. Схемная реализация суммирующего счетчика с М=10 (декадного счетчика)
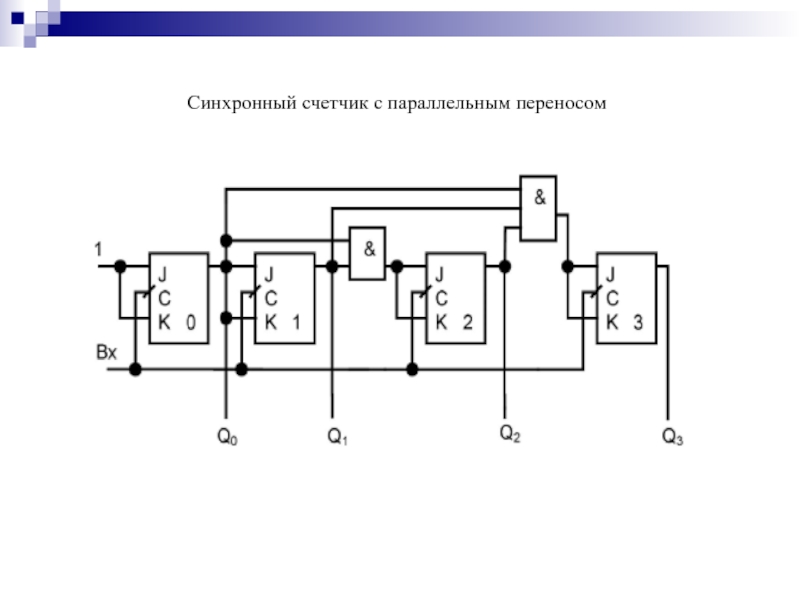
- 146. Синхронный счетчик с параллельным переносом
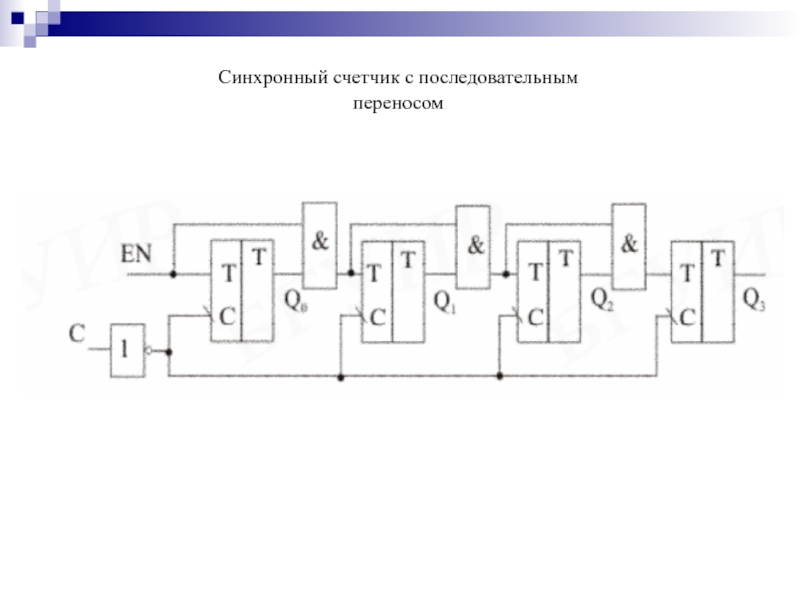
- 147. Синхронный счетчик с последовательным переносом
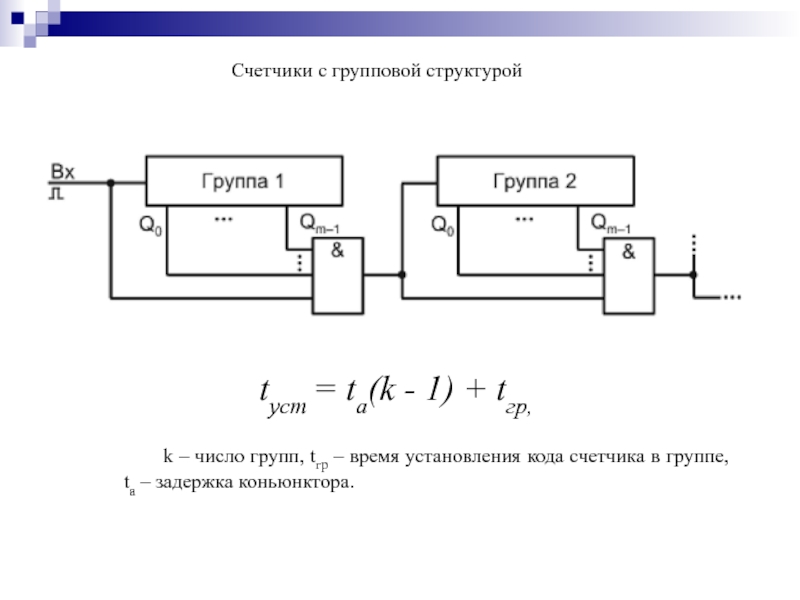
- 148. Счетчики с групповой структурой tуст = ta(k
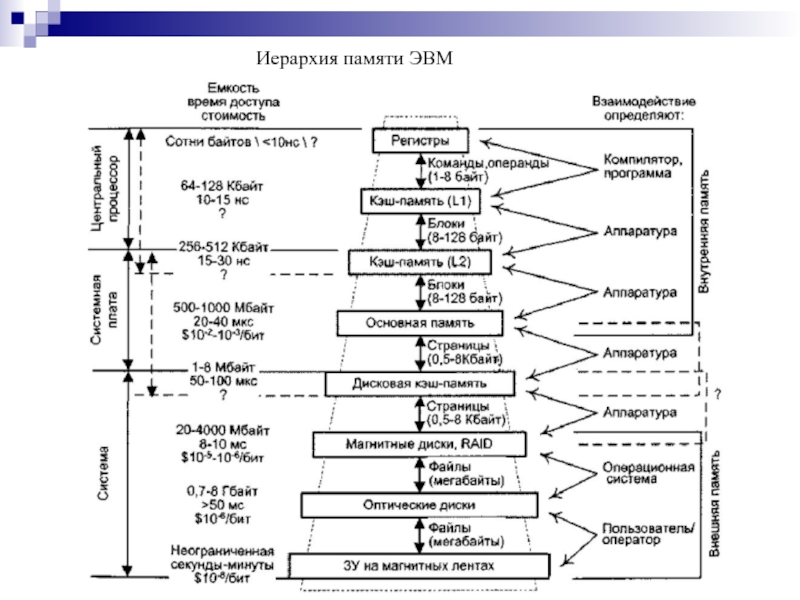
- 149. Иерархия памяти ЭВМ
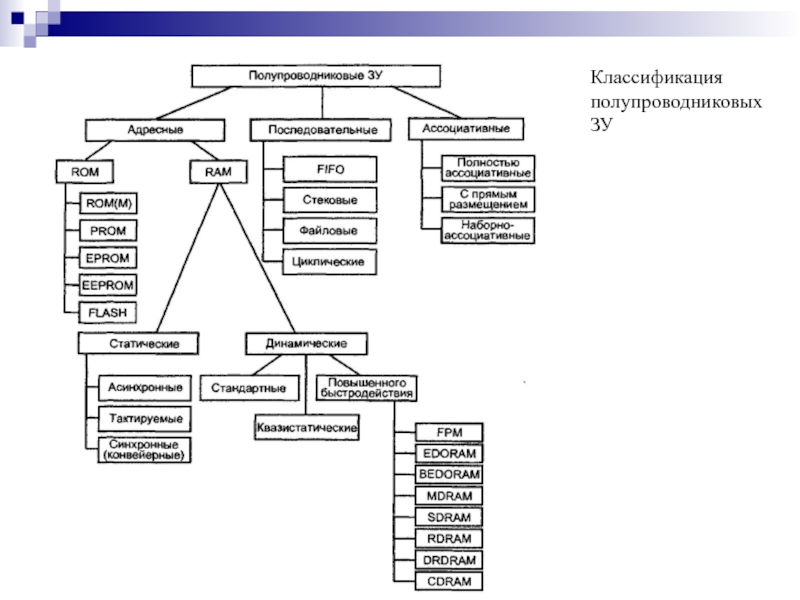
- 150. Классификация полупроводниковых ЗУ
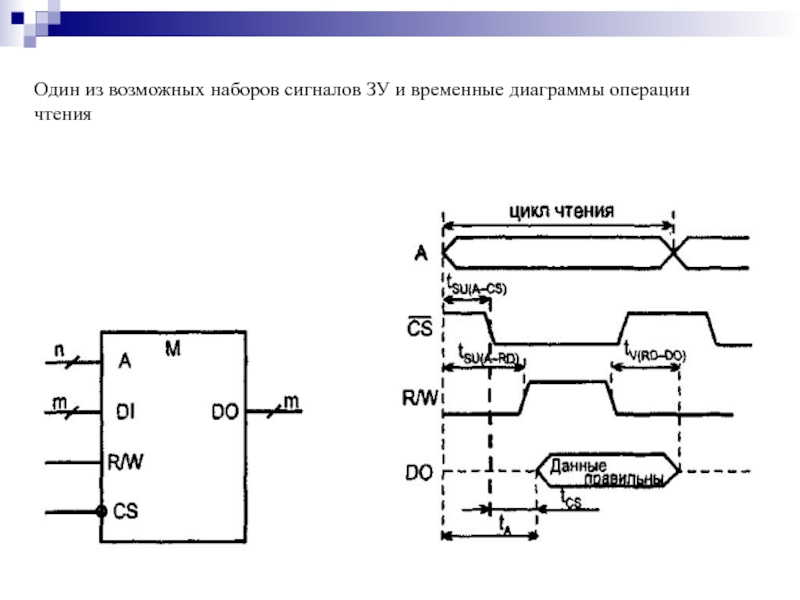
- 151. Один из возможных наборов сигналов ЗУ и временные диаграммы операции чтения
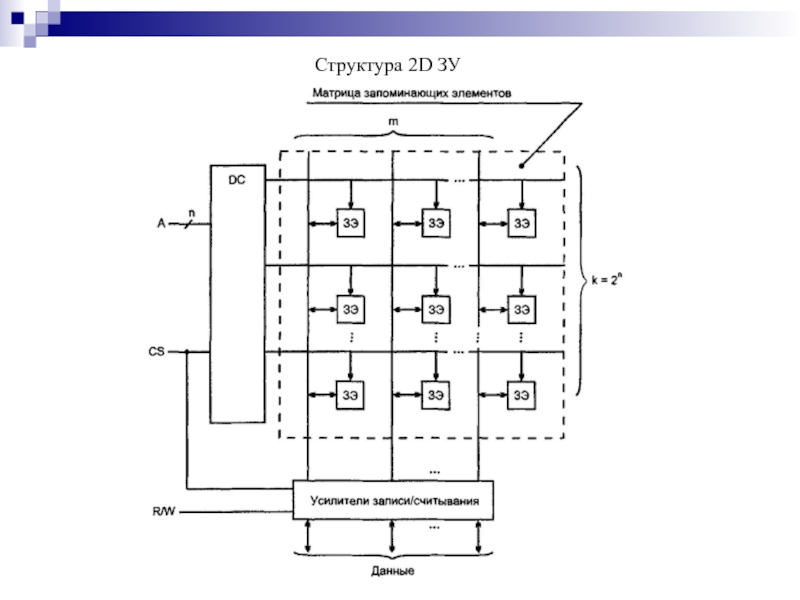
- 152. Структура 2D ЗУ
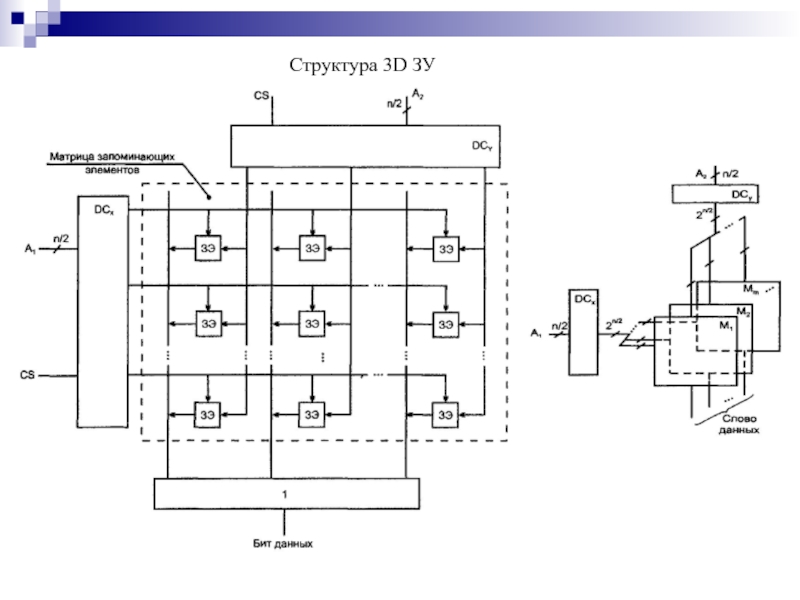
- 153. Структура 3D ЗУ
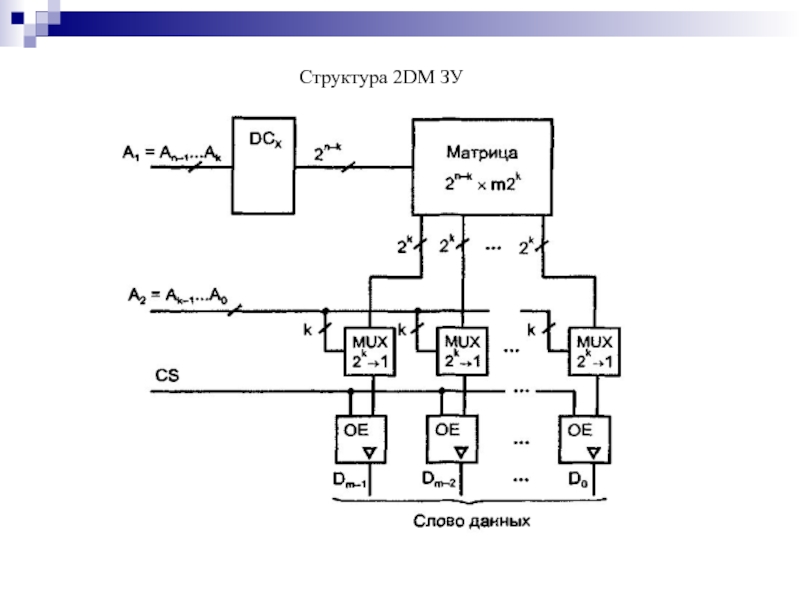
- 154. Структура 2DM ЗУ
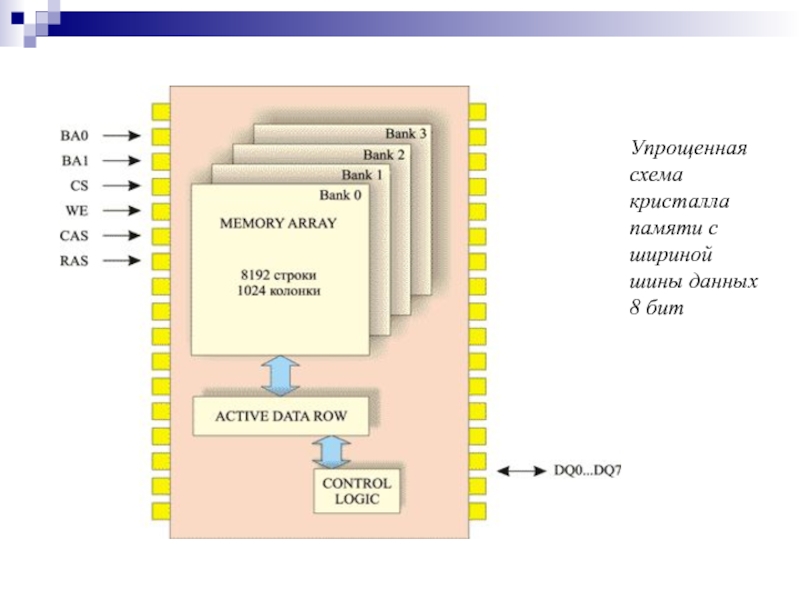
- 155. Упрощенная схема кристалла памяти с шириной шины данных 8 бит
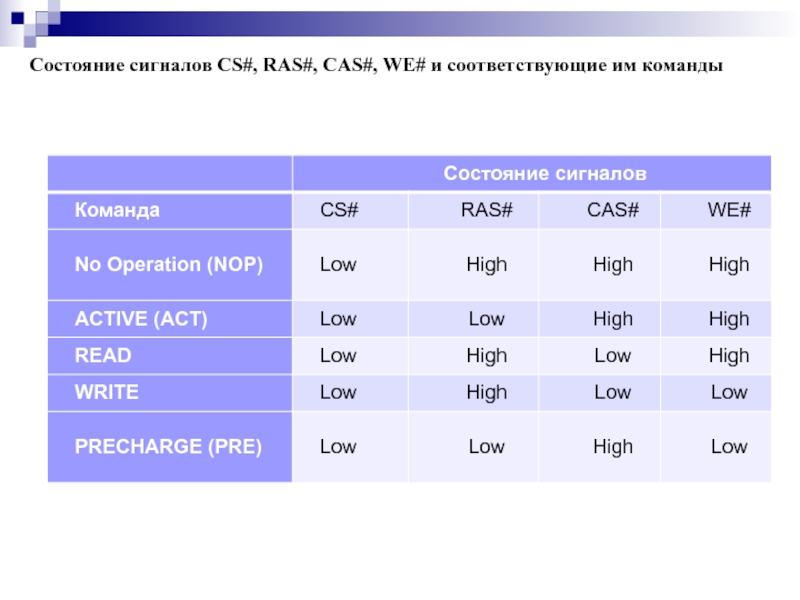
- 156. Состояние сигналов CS#, RAS#, CAS#, WE# и соответствующие им команды
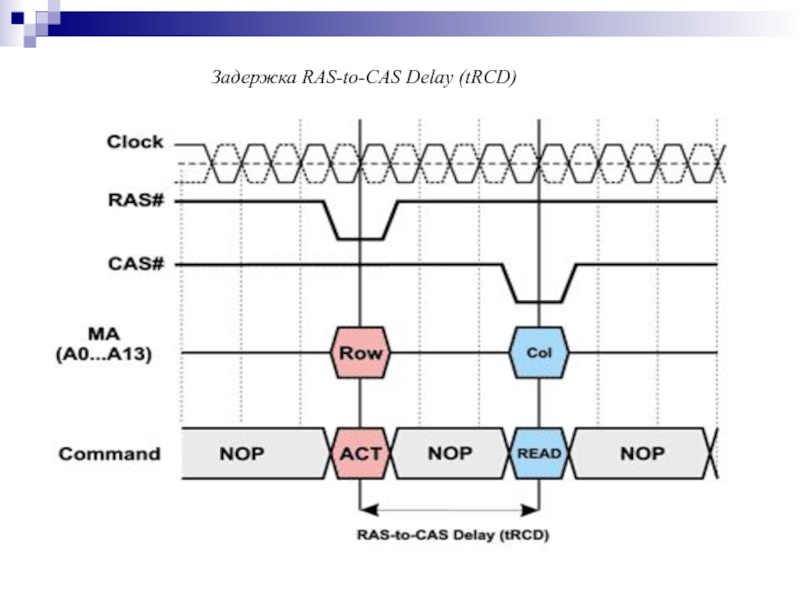
- 157. Задержка RAS-to-CAS Delay (tRCD)
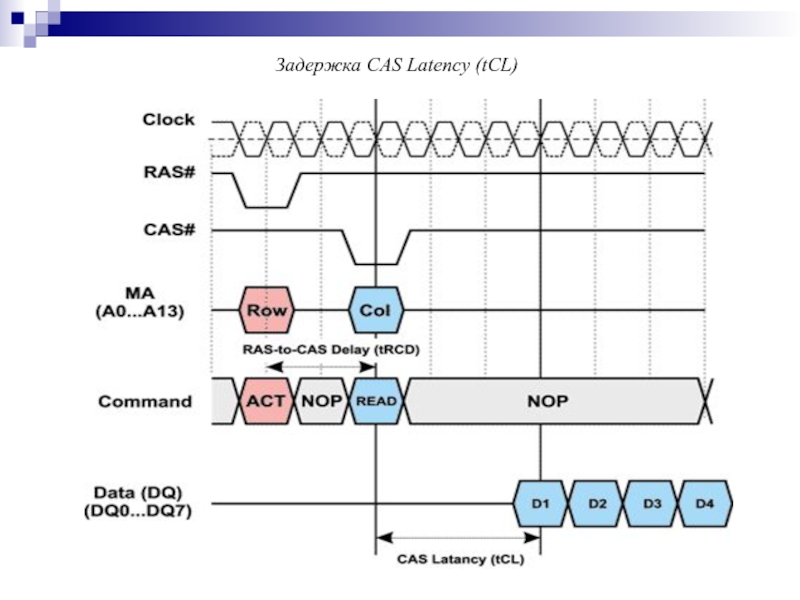
- 158. Задержка CAS Latency (tCL)
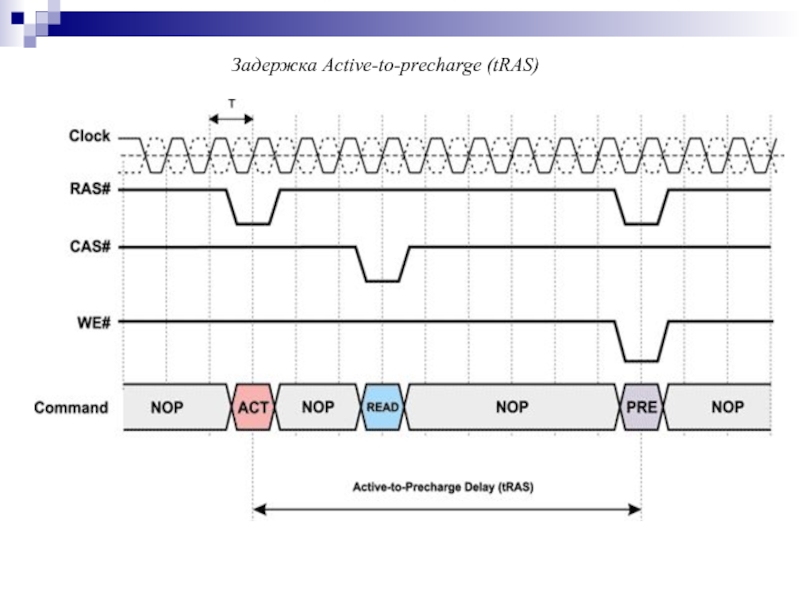
- 159. Задержка Active-to-precharge (tRAS)
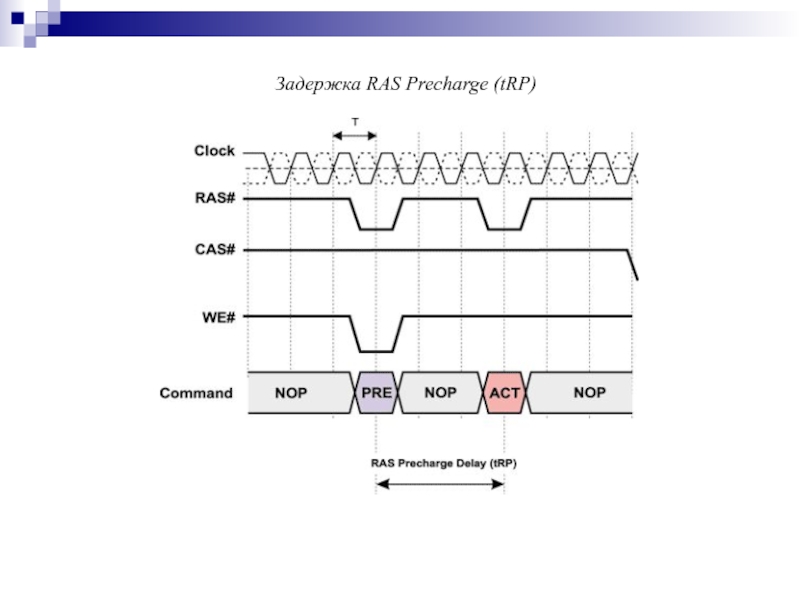
- 160. Задержка RAS Precharge (tRP)
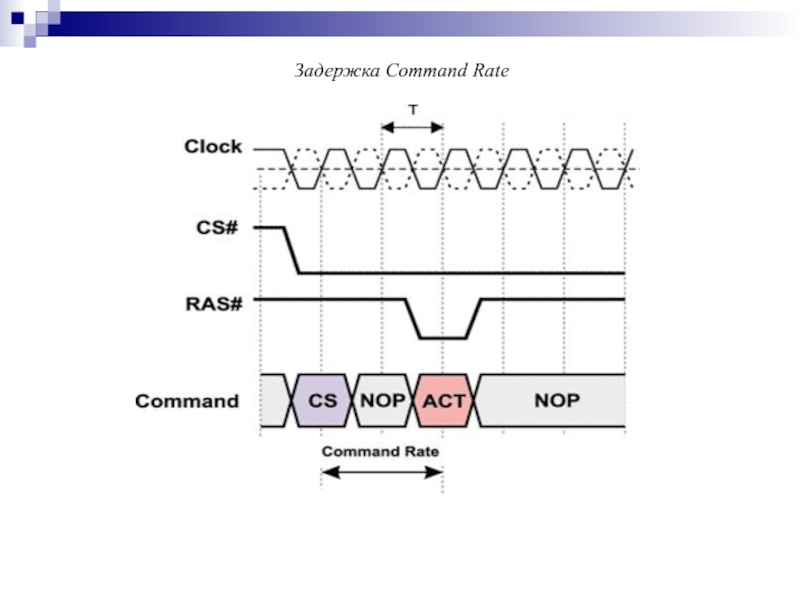
- 161. Задержка Command Rate
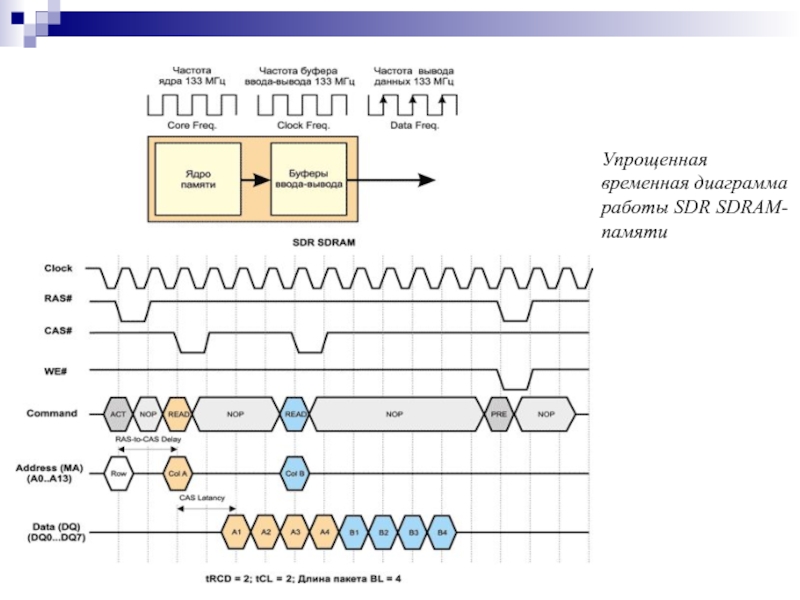
- 162. Упрощенная временная диаграмма работы SDR SDRAM-памяти
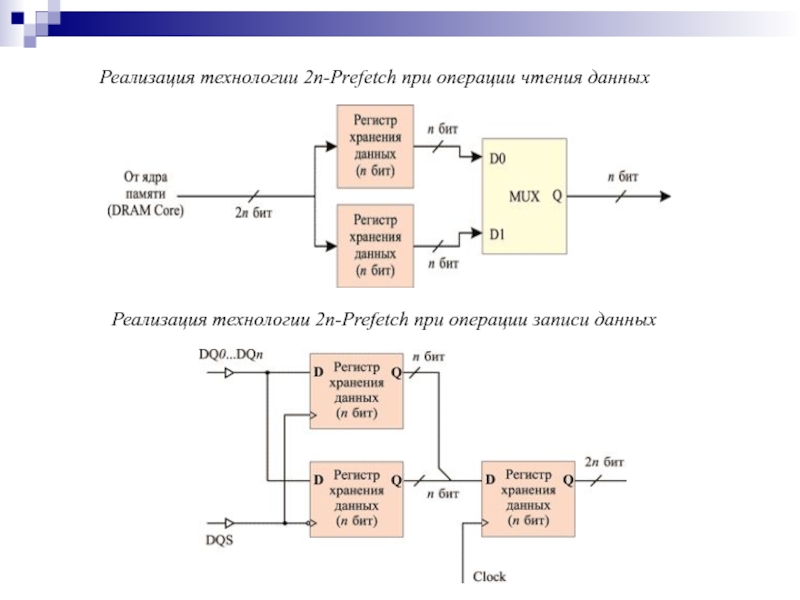
- 163. Реализация технологии 2n-Prefetch при операции чтения данных Реализация технологии 2n-Prefetch при операции записи данных
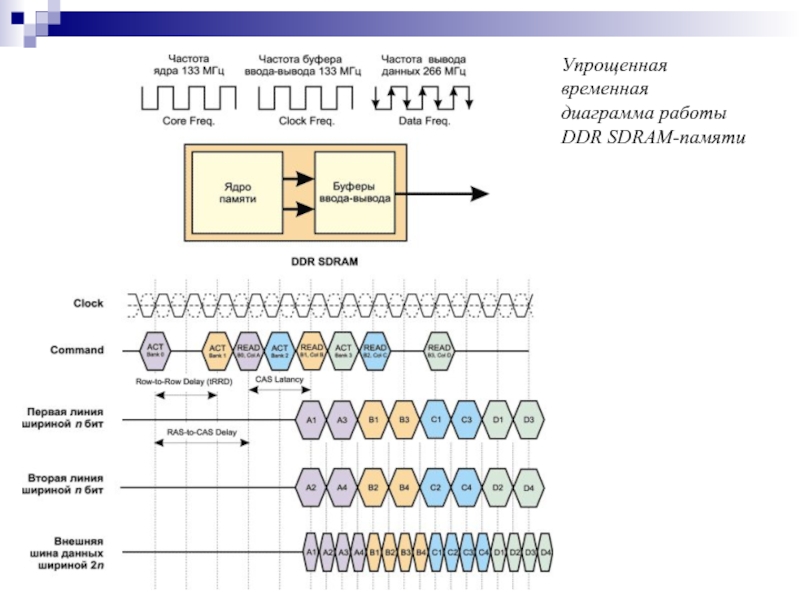
- 164. Упрощенная временная диаграмма работы DDR SDRAM-памяти
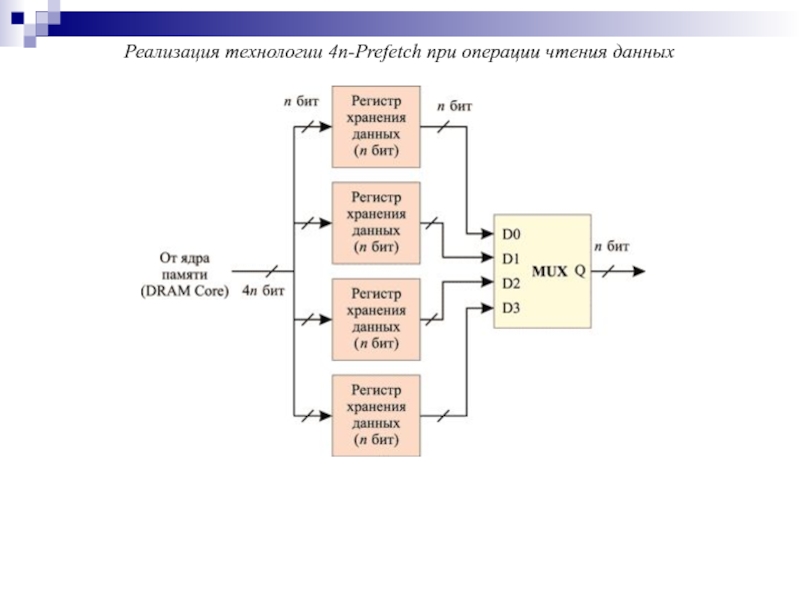
- 165. Реализация технологии 4n-Prefetch при операции чтения данных
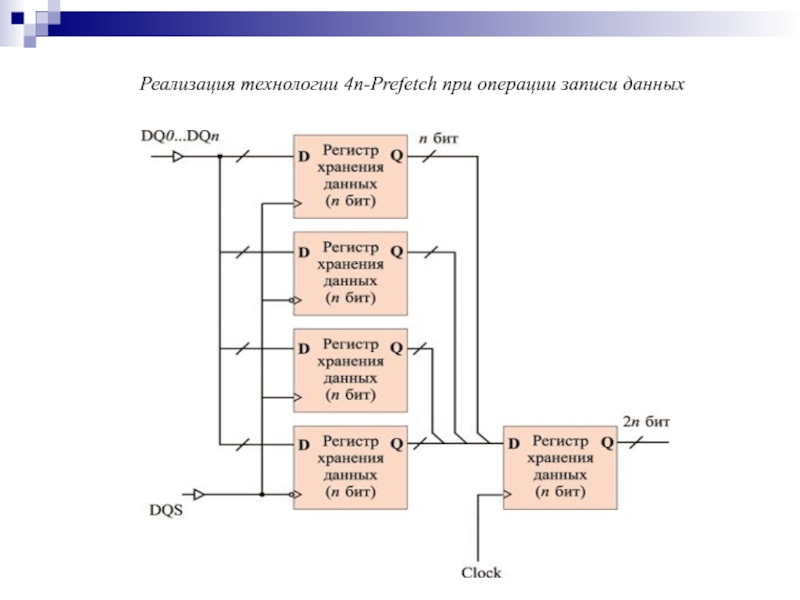
- 166. Реализация технологии 4n-Prefetch при операции записи данных
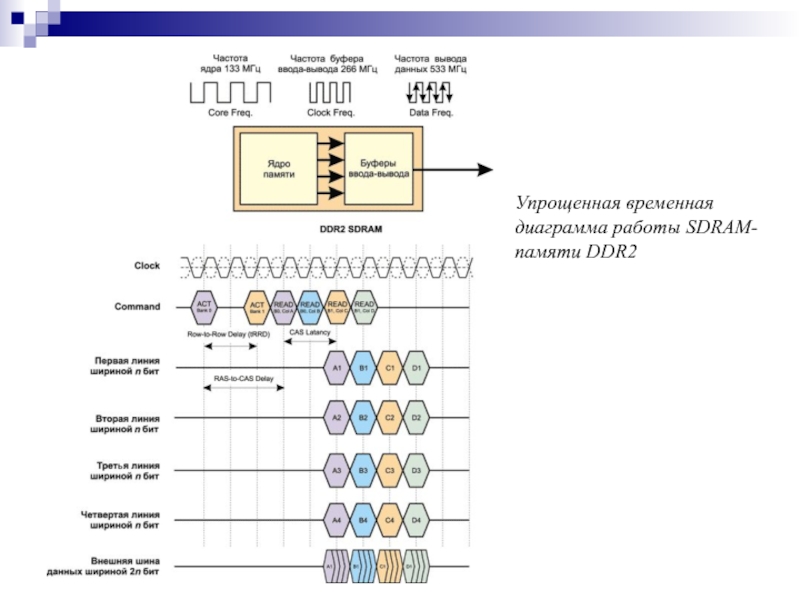
- 167. Упрощенная временная диаграмма работы SDRAM-памяти DDR2
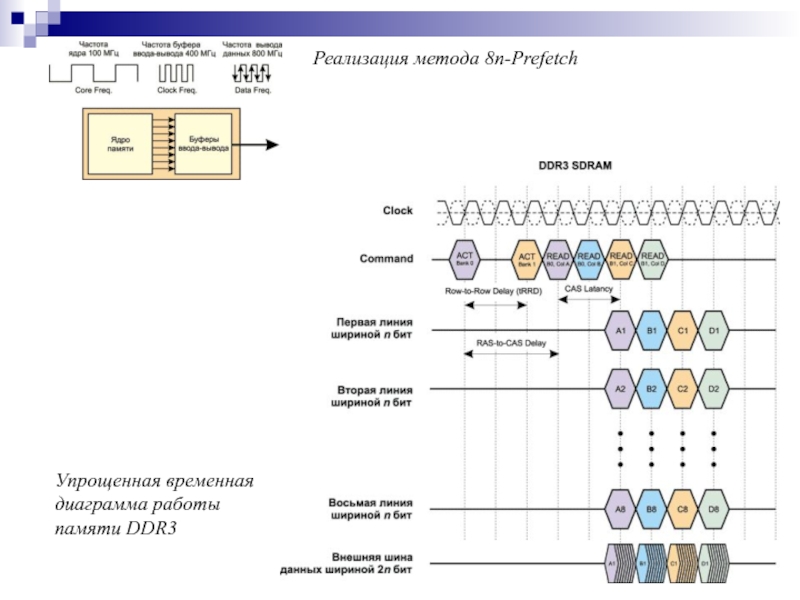
- 168. Реализация метода 8n-Prefetch Упрощенная временная диаграмма работы памяти DDR3
- 169. Абстрактный цифровой автомат Математической моделью систем с
- 170. Таблицы переходов (а) и выходов (б) автомата Мили Совмещенная таблица автомата Мили
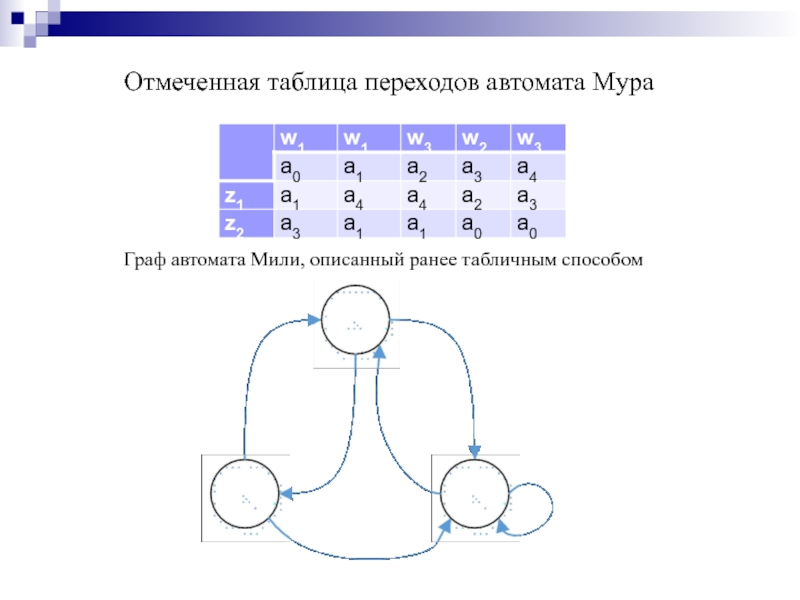
- 171. Отмеченная таблица переходов автомата Мура Граф автомата Мили, описанный ранее табличным способом
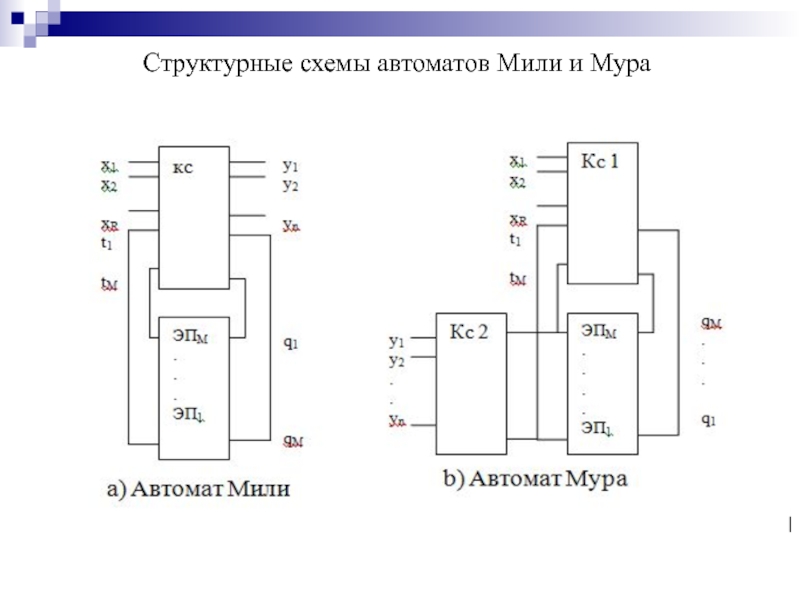
- 172. Структурные схемы автоматов Мили и Мура
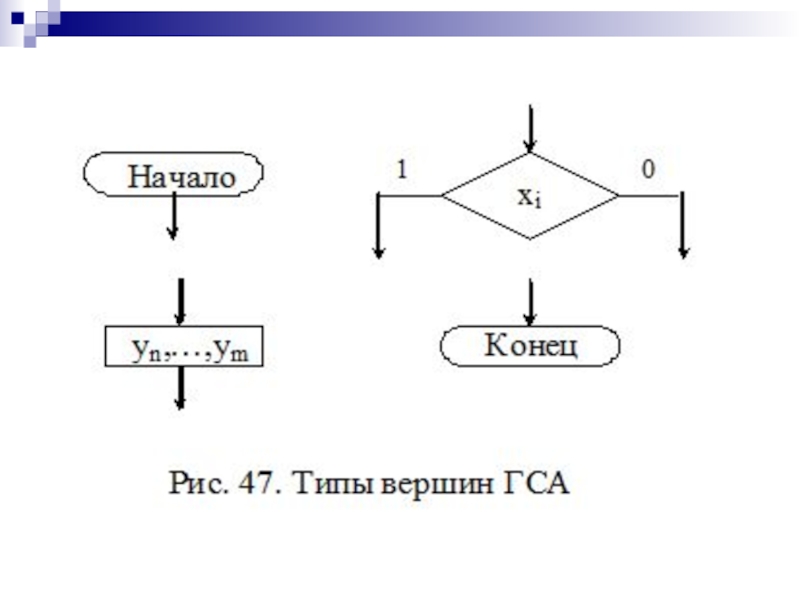
- 173. Структурный синтез частичного цифрового автомата Кодирование входных, выходных сигналов и внутренних состояний
- 174. Структурные таблицы переходов и выходов
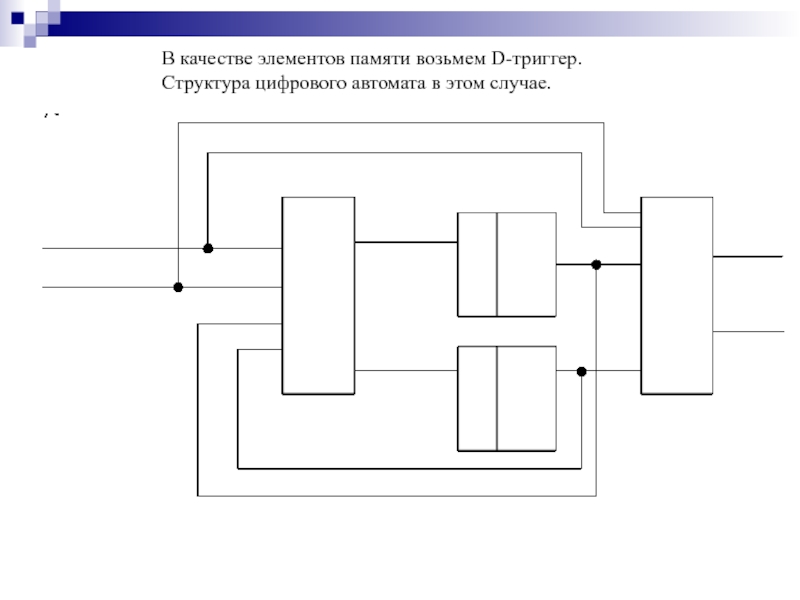
- 175. В качестве элементов памяти возьмем D-триггер. Структура цифрового автомата в этом случае.
- 176. Таблица истинности и логические функции y1 и у2
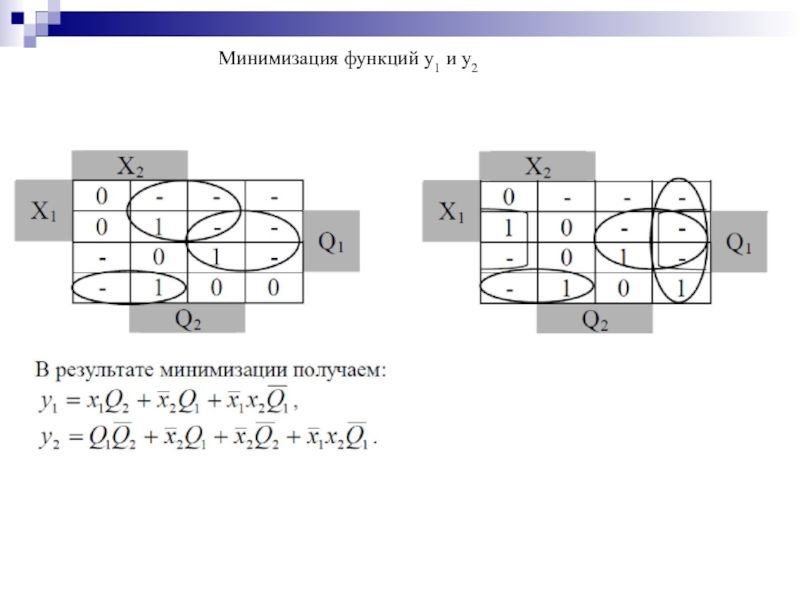
- 177. Минимизация функций y1 и у2
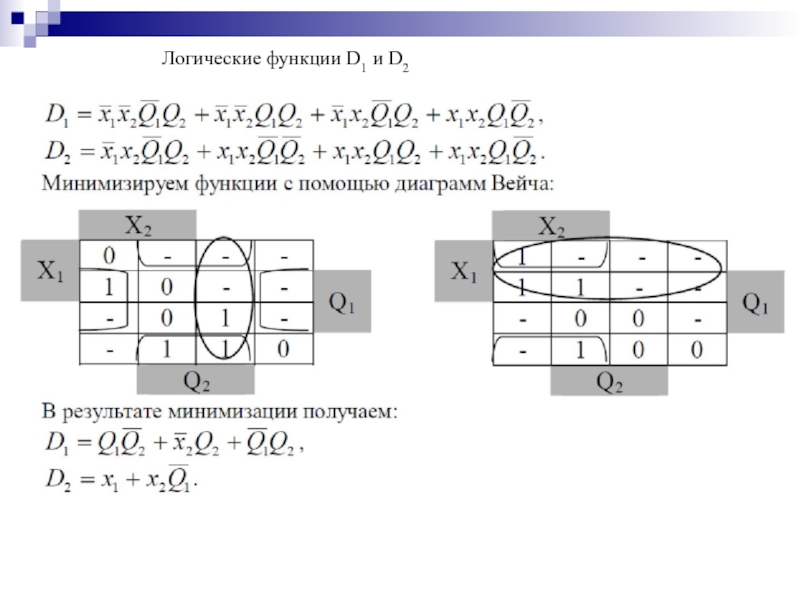
- 178. Логические функции D1 и D2
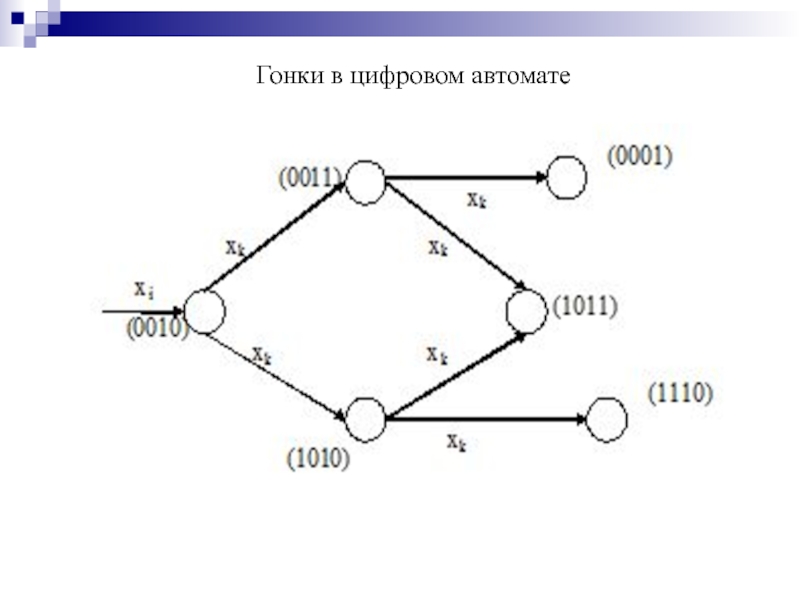
- 179. Гонки в цифровом автомате
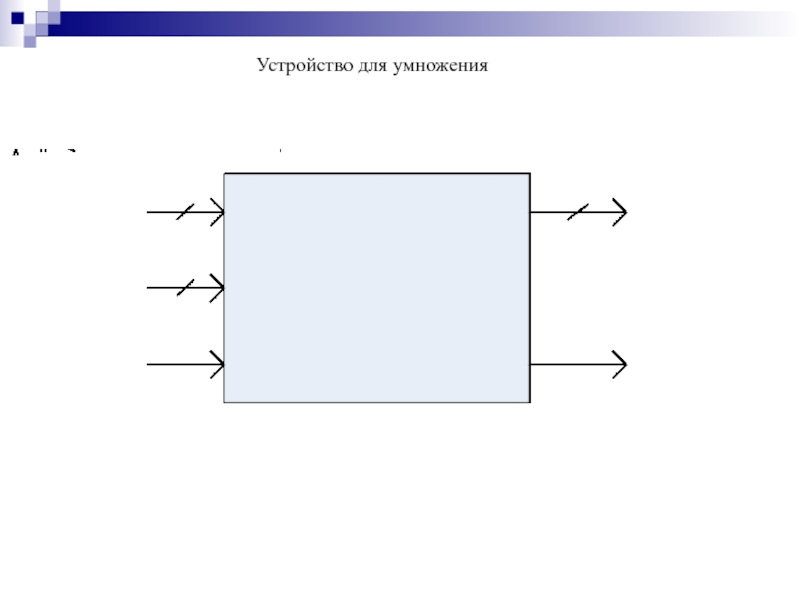
- 181. Устройство для умножения
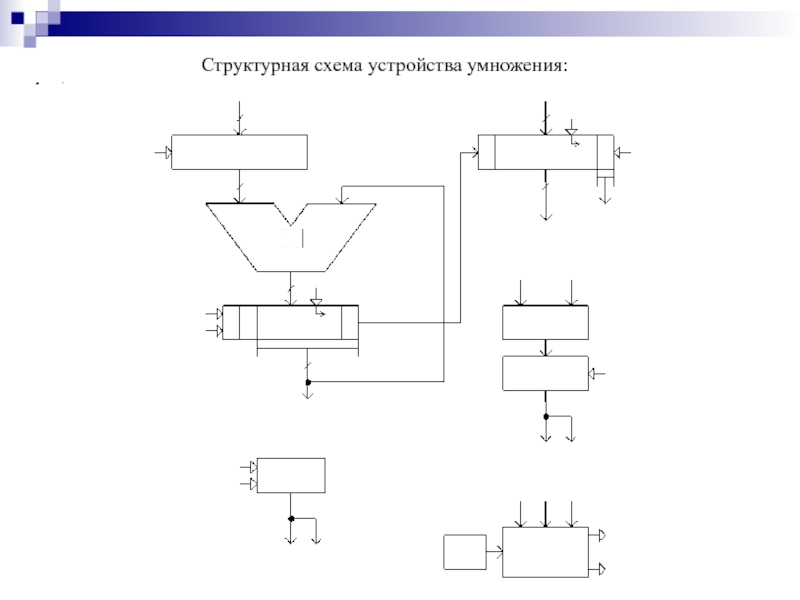
- 182. Структурная схема устройства умножения:
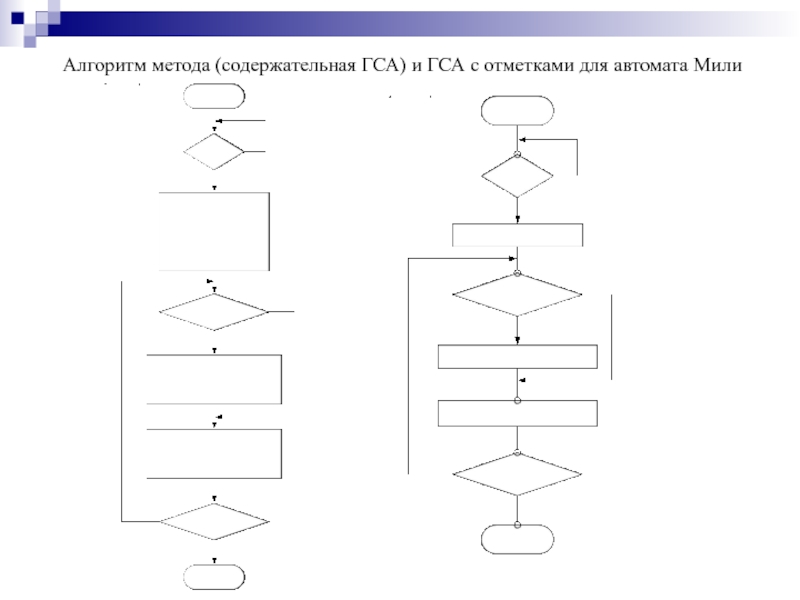
- 183. Алгоритм метода (содержательная ГСА) и ГСА с отметками для автомата Мили
- 184. Расширенная таблица переходов-выходов am – исходное
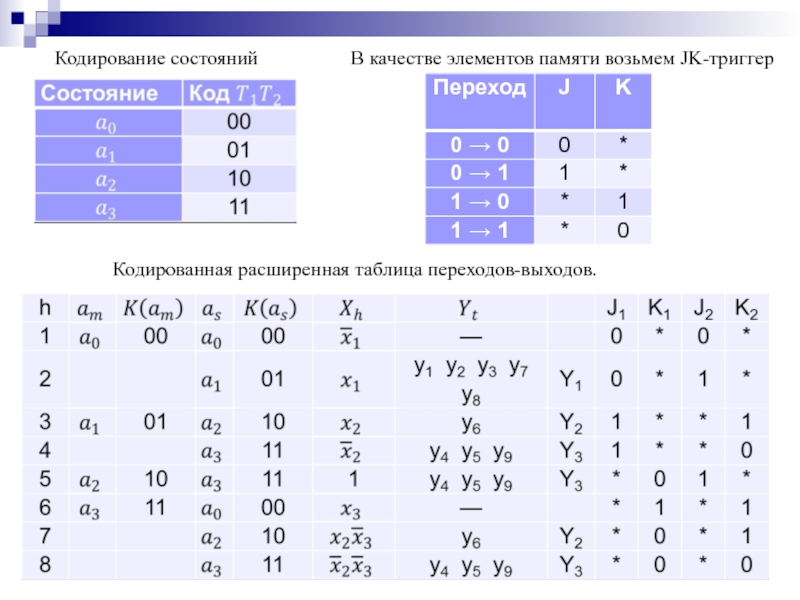
- 185. Кодирование состояний В качестве элементов памяти возьмем JK-триггер Кодированная расширенная таблица переходов-выходов.
- 186. Функции выходов и возбуждений элементов памяти:
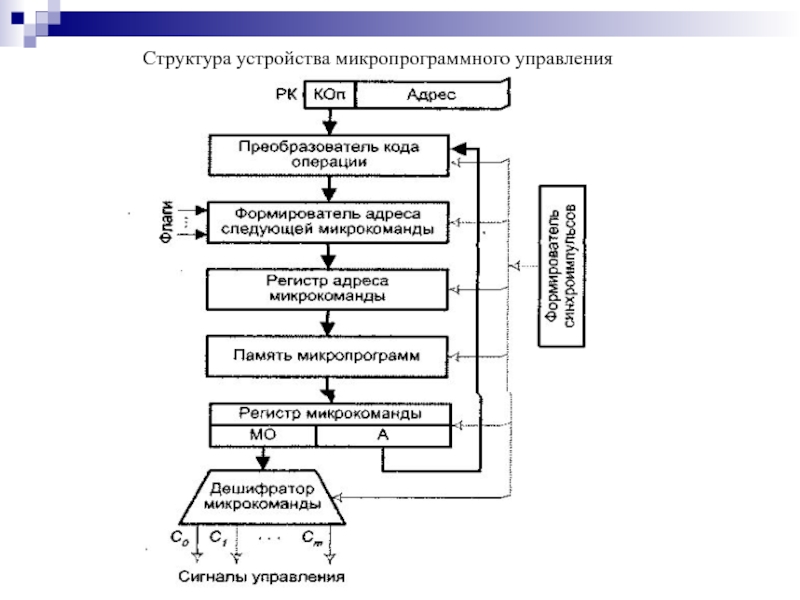
- 187. Структура устройства микропрограммного управления
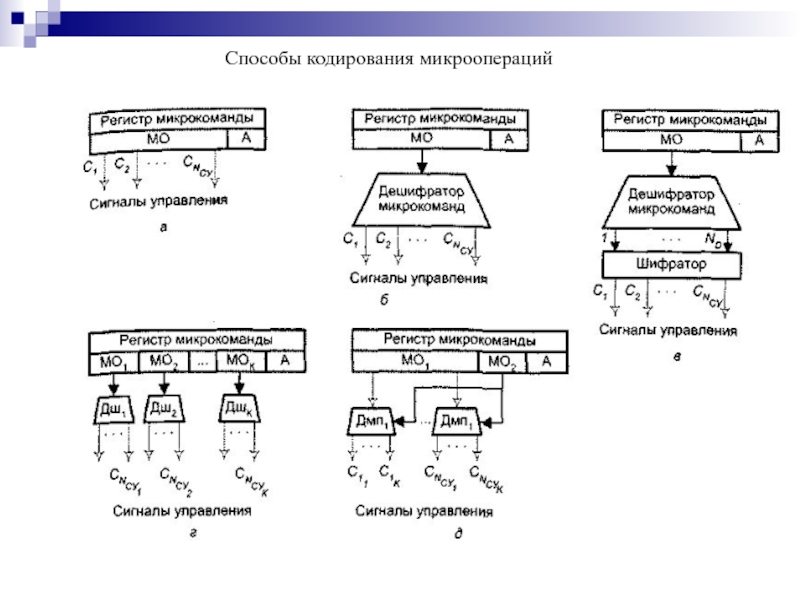
- 188. Способы кодирования микроопераций
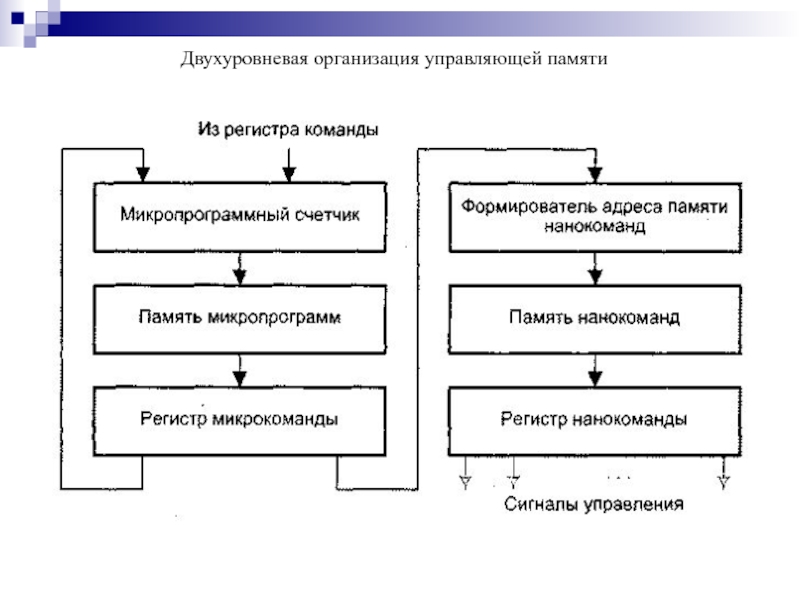
- 189. Двухуровневая организация управляющей памяти
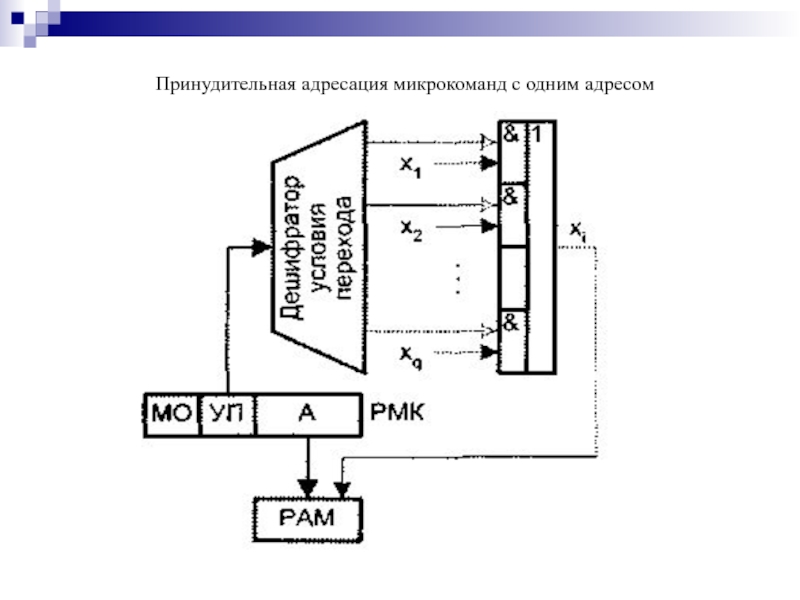
- 190. Принудительная адресация микрокоманд с одним адресом
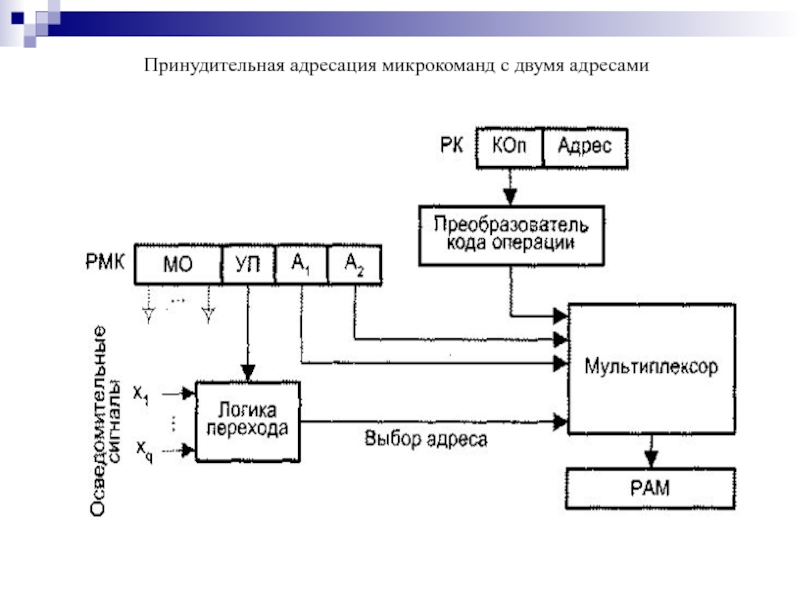
- 191. Принудительная адресация микрокоманд с двумя адресами
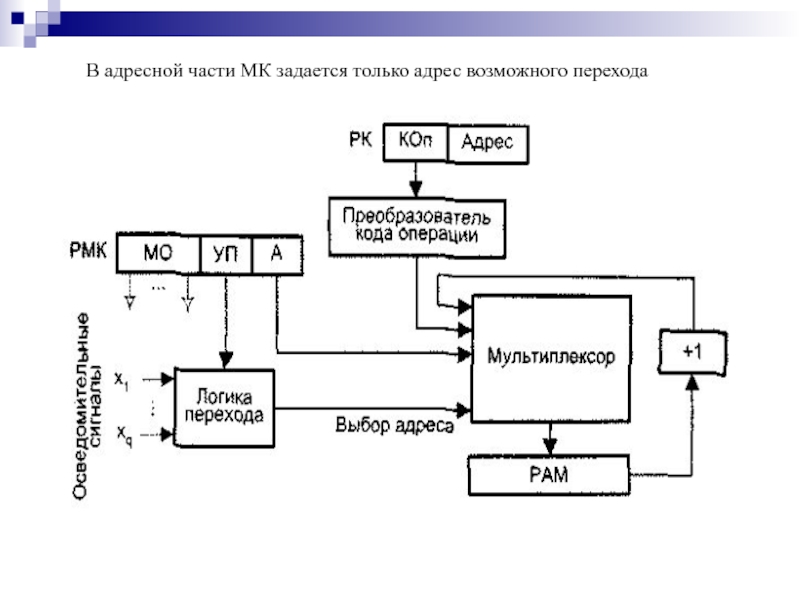
- 192. В адресной части МК задается только адрес возможного перехода
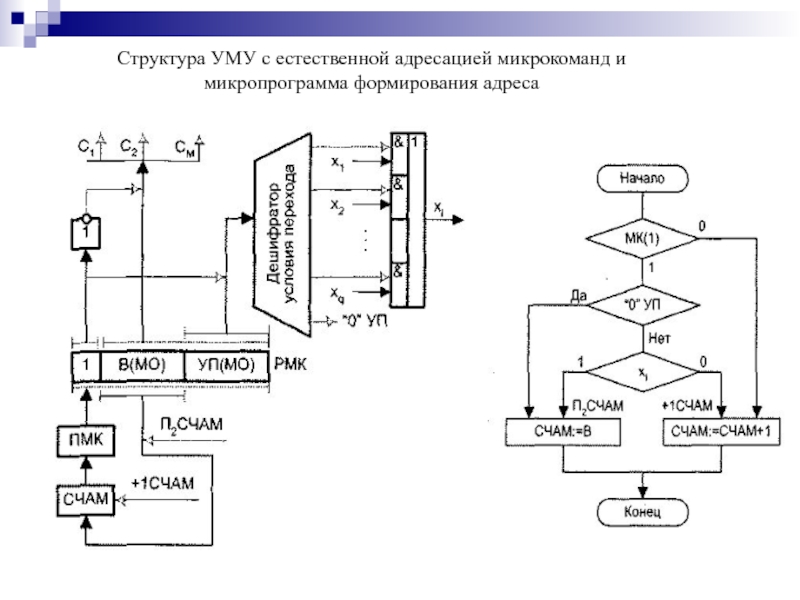
- 193. Структура УМУ с естественной адресацией микрокоманд и микропрограмма формирования адреса
Слайд 2Учебно-методические материалы
Точи Р.Дж., Уидмер Н.С. Цифровые системы. Теория и практика, 8-е
Пухальский Г.И., Новосельцева Т.Я. Цифровые устройства: Учебное пособие для втузов. -СПб.: Политехника, 1996.
Угрюмов Е.П. Цифровая схемотехника. - СПб.: БХВ – Санкт-Петербург, 2000.
Савельев А.Я. Прикладная теория цифровых автоматов: Учебник для вузов по спец. ЭВМ. -М.: Высшая школа, 1987.
Слайд 3Путков В.Н. и др. Электронные вычислительные устройства: Учеб. пособие для радиотехн.
Цилькер Б.Я., Орлов С.А. Организация ЭВМ и систем: Учебник для вузов. -СПб.: Питер, 2004.
Закревский А.Д., Поттосин Ю.В., Черемисинова Л.Д. Основы логического проектирования. Кн. 2. Оптимизация в булевом пространстве. -Мн.: ОИПИ НАН Беларуси, 2004.
Закревский А.Д., Поттосин Ю.В., Черемисинова Л.Д. Основы логического проектирования Кн. 3. Проектирование устройств логического управления. -Мн.: ОИПИ НАН Беларуси, 2006.
Слайд 4Позиционные системы счисления.
Позиционная система счисления – это система, в которой
Основание системы счисления – это количество S различных символов, используемых в пределах одного разряда.
В двоичной системе (S=2) используются символы 0,1.
В восьмеричной – символы 0,1, 2,…, 7.
В десятичной – символы 0,1,2,…,9.
В шестнадцатеричной – символы 0,…,9,A,B,C,D,E,F.
Числа в позиционных системах представляются последовательностью ряда цифр, разделенных на две группы: группа разрядов, задающая целую часть числа, и группа разрядов, задающая дробную часть.
Слайд 5Пусть
- число в системе счисления с основанием S.
Любое число X в
S – основание; i – номер разряда; n+1 (n, n-1, …, 1, 0) – количество целых разрядов; m – количество дробных разрядов; n - старший разряд; -m - младший разряд; ai - разрядные коэффициенты; Si - вес i-го разряда.
Пример. 71,25 = 7×101 +1×100,+2×10−1+5×10−2
Слайд 6В вычислительной технике применяется двоичная система (X =2), в ней для
Сложение
0+0=0;
0+1=1;
1+0=1;
1+1=10
Вычитание
0-0=0;
1-0=1;
1-1=0;
10-1=1
Умножение
0⋅ 0=0;
0⋅ 1=0;
1⋅ 0=0;
1⋅ 1=1
Деление чисел в двоичной системе производится по правилам умножения и вычитания.
Слайд 8Пример двоично-десятичного кода
0001 1001 1000 0100(D) = 1984(10)
Перевод из двоичной в
1) перевод 1101111001.11012 в восьмеричное
001 101 111 001 . 110 100 = 1571.648;
1 5 7 1 6 4
2) перевод 11111111011.1001112 в шестнадцатеричное
0111 1111 1011 . 1001 1100 = 7FB.9C16.
7 F B 9 C
Слайд 9Правило перевода целых чисел.
Пример. Перевести целое десятичное число 43 в двоичную
Следовательно, 4310 ==>1010112; 4310 ==> 2В16.
Слайд 10Перевод из недесятичной позиционной системы счисления в десятичную
Пример. Перевести двоичное число
Слайд 11Перевод дробей
Пример. Перевести десятичную дробь 0,375 в двоичную (а) и шестнадца-теричную
Следовательно, 0,37510 ==>0,0112; 0,375 10 ==>0,616.
Слайд 12Пример: десятичной дроби 0,7689 соответствует двоичная дробь 0,110001 с точностью
0,7689
x
1,5378
x 2
1,0756
x 2
0,1512
x 2
0,3024
х 2
0,6048
х 2
1,2096
Слайд 13Перевод неправильной дроби
Пример. Последовательно перевести число X=524,6 (8-ричная система счисления) в
Перевод (8) ? (10)
X=
Перевод (10) ? (2)
340/2=170(ост 0); 170/2=85(0); 85/2=42(1); 42/2=21(0); 21/2=10(1); 10/2=5(0); 5/2=2(1); 2/2=1(0). Целая часть 101010100
0,75x2=1,5; 0,5x2=1,0. Дробная часть 0,11
X=101010100,11
Слайд 14Перевод (2) ? (16)
(0001)(0101)(0100),(1100)
1 5
X=154,C.
Перевод (16) ? (10)
X=
Перевод (10) ? (8)
340/8=42(4); 42/8=5(2);
0,75x8=6,0
X=524,6
Слайд 15Основы алгебры логики
Рассмотрим некоторую функцию y =
от n аргументов, где
и функция y
принимает значение 0,1 из множества B={0,1}.
Булевой (логической) функцией называется двоичная функция от двоичных аргументов.
Булева функция задает отображение булева пространства (состоящего из
двоичных векторов) в множество {0,1}:
элементов – n-компонентных
Слайд 16Число всех булевых функций, зависящих от n аргументов, равно
Имеются только
Имеется 16 булевых функций от двух аргументов:
Функции (двухместные логические операции) дизъюнкции , коньнкции и отрицания (инверсии) образуют булеву алгебру.
Слайд 17Алгебру логики составляют следующие операции: одноместная операция отрицания (инверсирования) и двухместные
Слайд 19Основные законы и аксиомы (тождества) алгебры логики.
Закон исключенного третьего
Закон отрицания
Умножение на константу
Сложение с константой
Идемпотентность
Слайд 22Пример табличного задания функции от трех аргументов.
Три функции, зависящие от двух
Слайд 23Пример. Задано логическое выражение
Составить логическую схему для данного выражения и
Слайд 25Элементарной конъюнкцией называется логическое произведение любого конечного числа переменных, входящих в
являются элементарными конъюнкциями, а
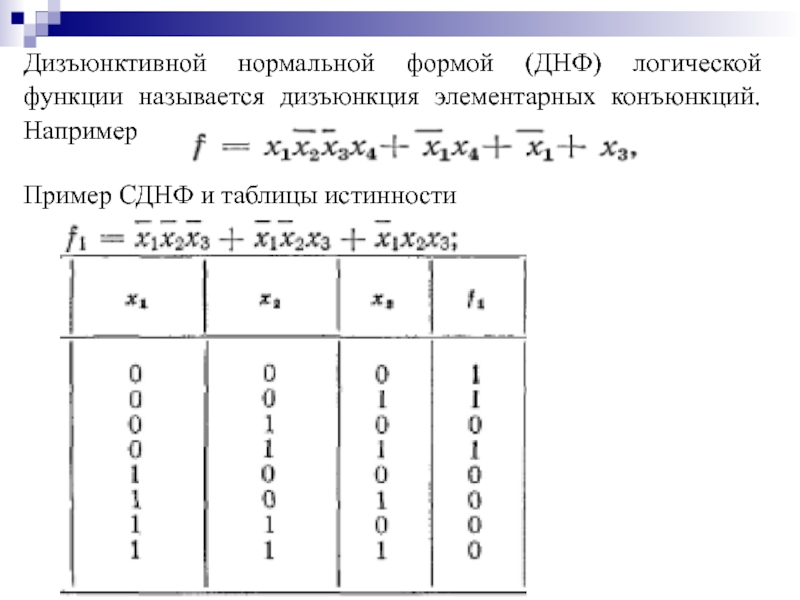
Слайд 26Дизъюнктивной нормальной формой (ДНФ) логической функции называется дизъюнкция элементарных конъюнкций. Например
Пример СДНФ и таблицы истинности
Слайд 28Конъюнктивной нормальной формой (КНФ) называется конъюнкция элементарных дизъюнкций. Например
Пример СКНФ
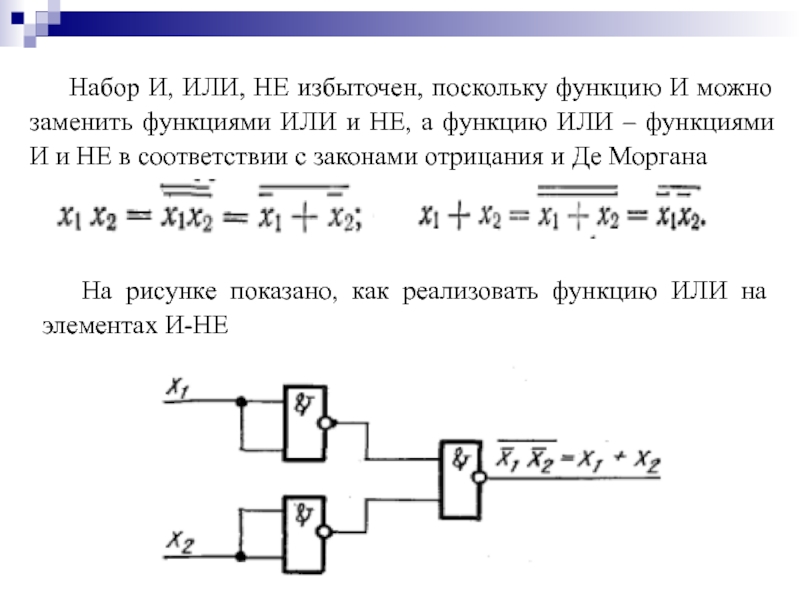
Слайд 29Набор И, ИЛИ, НЕ избыточен, поскольку функцию И можно заменить функциями
На рисунке показано, как реализовать функцию ИЛИ на элементах И-НЕ
Слайд 30Локальные методы упрощения ДНФ
Поглощение определяется формулой
Склеивание определяется формулой
Удаление литерала
Операция обобщенного склеивания
Дублирование элементарных конъюнкций
=
=
Слайд 31Импликанты x1x2 и x2x3 являются простыми импликантами функции f, а например,
Слайд 34Метод Квайна-Мак-Класки.
Позволяет существенно уменьшить число попарных сравнений конъюнкций. Для этого все
Например, при n=4 в группу с i=1 включаются конъюнкции вида
в группу с i=2 конъюнкции вида
Попарное сравнение при этом можно проводить только между соседними по номеру группами, поскольку склеивающиеся конъюнкции могут содержаться только в соседних по номеру группах. В остальном минимизация по методу Квайна-Мак-Класки совпадает с минимизацией по методу Квайна.
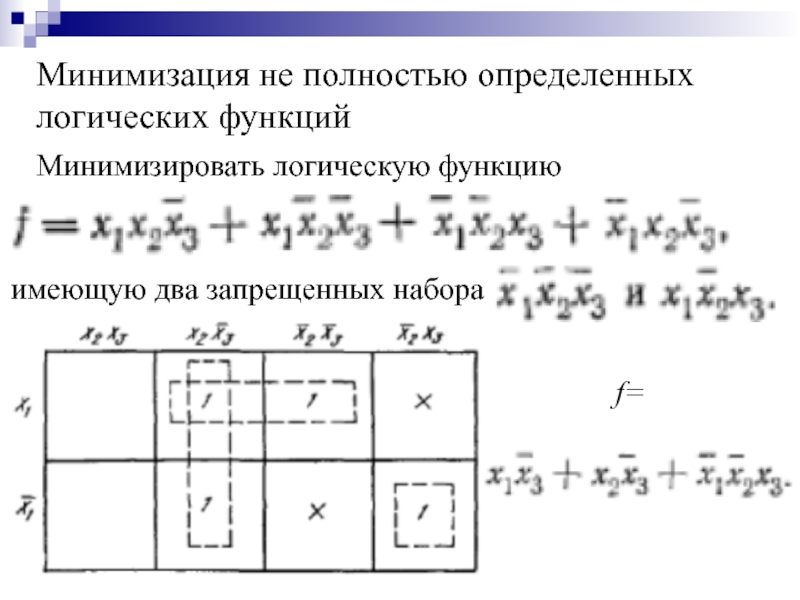
Слайд 38Минимизация не полностью определенных логических функций
Минимизировать логическую функцию
имеющую два запрещенных набора
f=
Слайд 41Формы представления чисел в ЭВМ и их кодирование
Представление чисел с фиксированной
В случае целых чисел минимальным по модулю отличным от нуля числом будет Аmin = 00…01, = 1, а максимальным, которому соответствуют единицы во всех n разрядах, – Amах = 11…11, = 2n - 1, т. е. диапазон представления чисел в этом случае 1 ≤ |A| ≤ 2n - 1.
Слайд 42В случае правильных дробей минимальным по модулю отличным от нуля числом
Представление чисел с фиксированной запятой
Слайд 43Представление чисел с плавающей запятой
В общем случае нормальная форма записи числа
где M – мантисса числа; r – основание системы счисления; p – порядок числа. Мантисса |М| < 1, т.е. является правильной дробью, а порядок р – целое число.
Слайд 44Нормализованные числа – числа для которых выполняется соотношение 1/r ≤ |M|
Представление чисел с плавающей запятой
В случае представления числа с плавающей запятой со смещенным порядком к его порядку p прибавляется целое число – смещение 2q, где q – число двоичных разрядов, используемых для представления модуля порядка,
pсм = p + 2q.
Слайд 45Наименьшее по модулю число с плавающей запятой с ненулевой нормализованной мантиссой
Представление чисел с плавающей запятой
а наибольшее по модулю число с плавающей запятой
Слайд 46Сравним диапазон представления чисел с фиксированной и плавающей запятой. Пусть, например,
231 - 1=2 147 483 647.
Для числа с плавающей запятой (n = 31, m = 24, q = 6 и два разряда используются для кодирования знаков мантиссы и порядка) максимальное значение числа равно (1 – 2-24) 264 – 1 ≈
1× 263 ≈ 1019.
Из сравнения этих двух значений вытекает, что при одинаковом числе разрядов n форма с плавающей запятой обеспечивает более широкий диапазон представления чисел.
Слайд 47Погрешности представления чисел
Для чисел с фиксированной запятой погрешность представления имеет место
Абсолютная погрешность перевода десятичной дроби в систему с основанием r при использовании усечения (младшие цифры справа отбрасываются) определяется следующим выражением
Для двоичной системы счисления r = 2, и максимальное значение этой погрешности получается при ai = 1
т.е. максимальная абсолютная ошибка равна значению младшего разряда.
Слайд 48При использовании округления максимальная абсолютная ошибка не превышает половины значения младшего
Погрешности представления чисел
Для представления чисел в форме с фиксированной запятой абсолютное значение машинного изображения правильной дроби находится в диапазоне
2-n ≤ |A|Ф ≤ 1 - 2-n.
Относительная погрешность представления для максимального значения числа равна
В современных ЭВМ, как правило, n = 16…64, поэтому 1>>2-n, откуда
Слайд 49Для минимального значения:
Погрешности представления чисел
откуда видно, что погрешности представления малых чисел
Слайд 50Для нахождения погрешностей представления чисел в форме с плавающей запятой величину
Погрешности представления чисел
Максимальная абсолютная ошибка не превышает половины значения младшего разряда мантиссы с учетом порядка, а относительная точность представления чисел в форме с плавающей запятой почти не зависит от величины числа.
Слайд 51Прямой код.
Правило образования прямого кода целого числа записывается в виде
n
Знаковый разряд занимает позицию с весом 2n.
Пример. n = 4
A1 = +1011; [A1]пр = 0.1011.
A2 = - 1011; [A2]пр = 1.1011.
Слайд 52Правило образования прямого кода правильной дроби записывается в виде
Знаковый разряд занимает
Пример. n = 4
A1 = +0,1010; [A1]пр = 0,1010.
A2 = - 0,1010; [A2]пр = 1,1010.
Нуль в прямом коде имеет два представления:
A = +00…00; [A]пр = 0.00…00.
A = - 00…00; [A]пр = 1.00…00.
Слайд 53Дополнительный код. В основе дополнительного кода n-разрядного отрицательного двоичного числа A
для целого числа до 2n: A′ = 2n - |A|;
для правильной дроби до 1: A′ = 1 - |A|.
Дополнительный код целого отрицательного n-разрядного числа A представляет собой дополнение до 2n+1 и определяется следующим образом
[A]доп = 2n+1 + A = 2n+1 - |A| = 2n + 2n - |A| = 2n + 2n - 1 - |A| + 1
код знака
дополнение A′
инверсия числа
Слайд 54Дополнительный код.
Пример. Записать дополнительный код числа A = - 101101,
10.000000 2n+1 1.000000 2n 1.000000 2n
- 101101 |A| - 101101 |A| - 1
1.010011 [A]доп 0.010011 A′ 0.111111
+ 1.000000 2n - 101101 |A|
1.010011 [A]доп 0.010010 инверсия |A|
+ 1
0.010011 A′
+ 1.000000 2n
1.010011 [A]доп
Слайд 55Дополнительный код отрицательной n-разрядной правильной дроби A представляет собой дополнение до
[A]доп = 2 + A = 2 - |A| = 1 + 1 - |A| = 1 + 1 – 2-n - |A| + 2-n
Пример. Записать дополнительный код числа A = - 0,101101, n = 6.
10,000000 2 1,000000 1,000000
- 0,101101 |A| - 0,101101 |A| - 0,000001 2-n
1,010011 [A]доп 0,010011 A′ 0,111111
+ 1,000000 - 0,101101 |A|
1,010011 [A]доп 0,010010 инверсия |A|
+ 0,000001 2-n
0,010011 A′
+ 1,000000
1,010011 [A]доп
Нуль в дополнительном коде имеет одно представление: 0.00…00.
Слайд 56Обратный код. В основе обратного кода n-разрядного отрицательного двоичного числа A
для целого числа до 2n - 1: A" = 2n - 1 - |A| (инверсия |A|);
для правильной дроби до 1 – 2-n: A" = 1 - 2-n - |A| (инверсия |A|).
Обратный код целого отрицательного n-разрядного числа A представляет собой дополнение до 2n+1 без единицы младшего разряда и определяется следующим образом
[A]обр = 2n+1 - 1 + A = 2n+1 -1 - |A| = 2n + 2n - 1 - |A|
Пример. Записать обратный код числа A = - 101101, n = 6.
10.000000 2n+1 1.000000 2n
- 1 - 1
1.111111 0.111111
- 101101 |A| - 101101 |A|
1.010010 [A]обр 0.010010 A" = инверсия |A|
+ 1.000000 2n
1.010010 [A]обр
Слайд 57Обратный код отрицательной n-разрядной правильной дроби A представляет собой дополнение до
[A]обр = 2 - 2-n + A = 2 - 2-n - |A| = 1 + 1 - 2-n - |A|
Пример. Записать обратный код числа A = - 0,101101, n = 6.
10,000000 2 1,000000
- 0,000001 2-n - 0,000001 2-n
1,111111 0,111111
- 0,101101 |A| - 0,101101 |A|
1,010010 [A]обр 0,010010 A" = инверсия |A|
+ 1,000000
1,010010 [A]обр
Нуль в обратном коде имеет два представления:
A = +00…00; [A]обр = 0.00…00.
A = - 00…00; [A]обр = 1.11…11.
Слайд 58Двоично-кодированное представление десятичных чисел
Наиболее часто используется такое двоично-кодированное представление десятинного числа
где aj – j-я десятичная цифра,
– i-й разряд j-ой тетрады,
n – количество десятичных цифр.
Количество различных Д-кодов определяется количеством возможных сочетаний по 10 из 16 комбинаций, которые допускает тетрада.
Слайд 59При образовании Д-кода следует исходить из общих требований, предъявляемых к системам
различным десятичным цифрам должны соответствовать различные тетрады;
большая десятичная цифра должна изображаться большей тетрадой, если разряды тетрады имеют веса по двоичной системе счисления;
для двух десятичных цифр и ,
связанных соотношением a + b = 9, должно удовлетворяться условие
(i = 0, 1, 2, 3);
Коды, обладающие таким свойством, называют самодополнительными.
4) для однозначности перевода чисел в Д-код и обратно желательно, чтобы разряды тетрад имели определенный вес. Тогда значение десятичной цифры a, соответствует выражению
где σ3, σ2, σ1, σ0 – веса соответствующих разрядов тетрады.
Слайд 61Американский стандартный код для обмена информацией ASCII (American Standard Code for
Слайд 64В настоящее время для всех ЭВМ рекомендован стандарт, разработанный общепризнанным международным
Стандарт определяет 32-битовый (одинарный) и 64-битовый (двойной) форматы
Слайд 66Двоичная арифметика с фиксированной запятой
Правила выполнения арифметических действий в двоичной системе
сложение вычитание умножение
0 + 0 = 0 0 - 0 = 0 0 × 0 = 0
0 + 1 = 1 1 - 0 = 1 0 × 1 = 0
1 + 0 = 1 1 - 1 = 0 1 × 0 = 0
1 + 1 = (1)0 0 - 1 = (1)1 1 × 1 = 1
перенос заем
в старший разряд из старшего разряда
Слайд 67Правила поразрядных действий при сложении двух двоичных чисел А + В представлены в
Слайд 68Правила поразрядных действий при вычитании двух двоичных чисел А - В представлены в
Слайд 69Пример. Сложить два числа в прямых кодах: A = +1011, B
Решение. [A]пр = 0.1011; [B]пр = 0.0100
1011 |A|
+ 0100 |B|
1111 |A + B|
[A + B]пр = 0.1111
Ответ: A + B = +1111.
Слайд 70Сумма дополнительных кодов чисел есть дополнительный код суммы чисел.
Доказательство. Предположим, что
Слайд 72Пример. Сложить два числа в обратных кодах: A = +1001, B
Решение. [A]обр = 0.1001; [B]обр = 1.1010
0.1001 [A]обр
+ 1.1010 [B]обр
10.0011
+ 1 циклический перенос
0.0100 [A + B]доп = [A + B]пр
Ответ: A + B = +100.
Пример. Сложить два числа в дополнительных кодах: A = +1001, B = -101, n = 4.
Решение. [A]доп = 0.1001; [B]доп = 1.1011
0.1001 [A]доп
+ 1.1011 [B]доп
10.0100 [A + B]доп = [A + B]пр
Ответ: A + B = +100.
отбрасывается
Слайд 73Пример. Сложить два отрицательных числа в дополнительных кодах:
A =
Решение. [A]доп = 1.0101; [B]доп = 1.0011
1.0101 [A]доп
+ 1.0011 [B]доп
10.1000 [A + B]доп переполнение.
отбрасывается
Пример. Сложить два дробных отрицательных числа в дополнительных кодах:
A = -0,1011, B = -0,0101, n = 4.
Решение. [A]доп = 1.0101; [B]доп = 1.1011
1.0101 [A]доп
+ 1.1011 [B]доп
11.0000 [A + B]доп переполнение.
отбрасывается
Слайд 74Пример. Записать в модифицированном коде: а) положительное число А = +1011;
Решение:
а)
б)
.
Слайд 75Пример. Сложить два отрицательных числа в модифицированных дополнительных кодах: A =
Решение. [A]доп = 11.0110; [B]доп = 11.0011
11.0110 [A]доп
+ 11.0011 [B]доп
110.1001 [A + B]доп комбинация 10 указывает на переполнение.
отбрасывается
Слайд 76Умножение, начиная с младших разрядов множителя, при сдвиге множимого влево и
Алгоритм умножения включает следующие шаги:
обнуление СЧП0;
анализ младшего разряда множителя: если b0 = 1, выполняется сложение ЧП0 = A с СЧП0 и переход к п. 3; если b0 = 0, сразу переход к п. 3;
сдвиг множимого влево;
анализ очередного разряда множителя: если b1 = 1, выполняется сложение ЧП1·21 с СЧП1 и переход к п. 5; если b1 = 0, непосредственно переход к п. 5;
сдвиг множимого влево;
анализ очередного bi разряда множителя и т.д. После анализа старшего bn-1 разряда множителя осуществляется последнее сложение ЧПn-1·2n-1 с суммой частичных произведений СЧПn-1 (если bn-1 = 1), и процесс прекращается. Результирующая СЧПn является искомым произведением.
Слайд 77Умножение, начиная со старших разрядов множителя, при сдвиге суммы частичных произведений
Применив схему Горнера, выражение для произведения можно записать следующим образом:
Выражения в скобках в формуле представляют собой последовательные значения СЧПi, определяемые рекуррентной формулой
Алгоритм умножения включает следующие шаги:
обнуление СЧП0;
сдвиг СЧП0 влево;
анализ старшего разряда множителя: если bn-1 = l, выполняется сложение ЧПn-1 = A с СЧП0·21 и переход к п. 4; если bn-1 = 0, сразу переход к п. 4;
сдвиг СЧП1 влево;
анализ очередного bn-2 разряда множителя и т.д. После анализа младшего b0 разряда множителя выполняется последнее сложение ЧП0 = A с СЧПn-1 (если b0 = 1), и процесс прекращается.
Слайд 78Умножение, начиная со старших разрядов множителя, со сдвигом множимого вправо и
– множимое, сдвинутое влево на n разрядов.
Алгоритм умножения включает следующие шаги:
обнуление СЧП0;
сдвиг множимого вправо;
анализ старшего разряда множителя: если bn-1 = 1, выполняется сложение ЧПn-1·2-1 с СЧП0 и переход к п. 4; если bn-1 =0, сразу переход к п. 4;
сдвиг множимого вправо;
анализ очередного разряда bn-2 множителя и т.д. После анализа младшего разряда b0 множителя осуществляется последнее сложение ЧП0·2-1 с СЧП (если b0 =1), и процесс прекращается.
Слайд 79Умножение, начиная с младших разрядов множителя, со сдвигом суммы частичных произведений
Применив схему Горнера к методу 3, выражение для произведения можно записать следующим образом:
Алгоритм умножения включает следующие шаги:
обнуление СЧП0;
анализ младшего разряда множителя: если b0 = 1, сложение ЧП0 = V с СЧП0 и переход к п. 3; если b0 = 0, непосредственно переход к п. 3;
сдвиг СЧП1 вправо;
анализ очередного разряда b1 множителя и т.д. После анализа старшего разряда bn-1 множителя осуществляются последнее сложение ЧПn-1 с СЧП n-1 (если bn-1 = l) и последний сдвиг СЧПn вправо, после чего процесс прекращается.
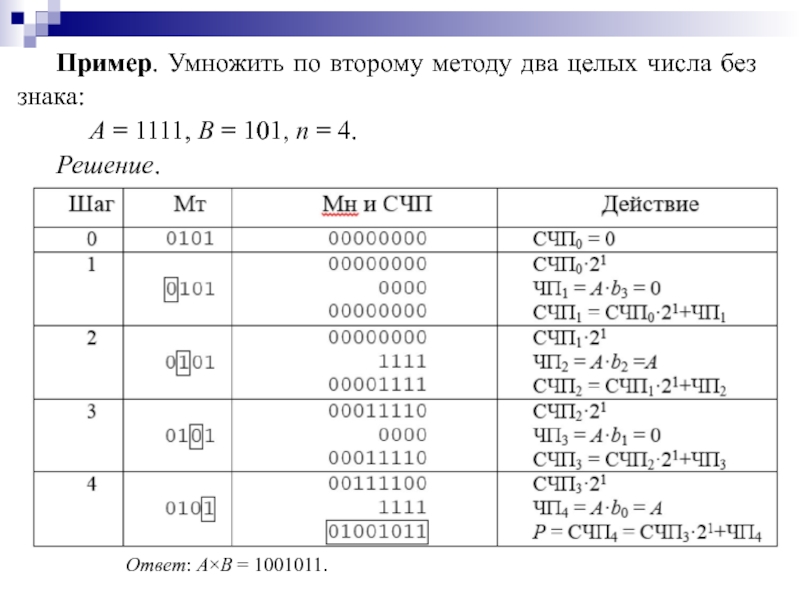
Слайд 80Пример. Умножить по второму методу два целых числа без знака:
Решение.
Ответ: A×B = 1001011.
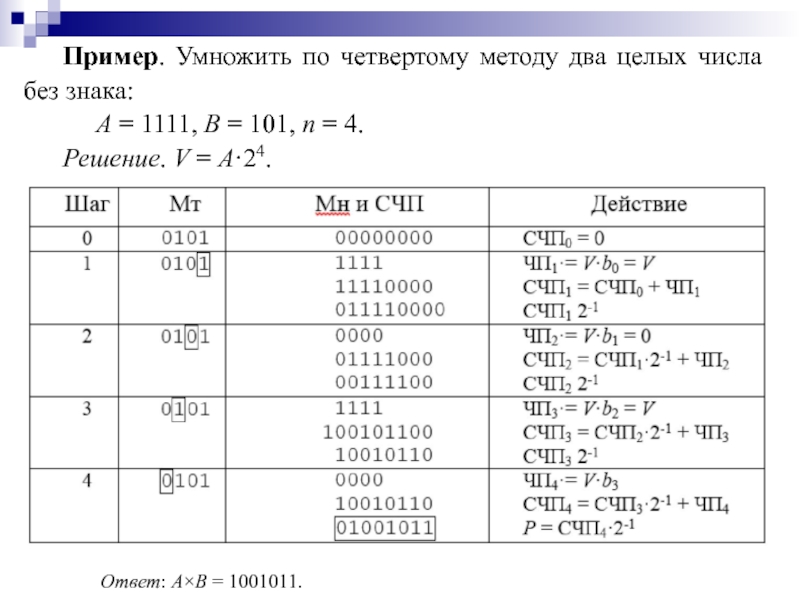
Слайд 81Пример. Умножить по четвертому методу два целых числа без знака:
Решение. V = A·24.
Ответ: A×B = 1001011.
Слайд 82Множимое произвольного знака, множитель положительный.
Пример. Умножить два целых числа со знаком
Решение. Умножение будем выполнять по четвертому методу.
[A]доп = 1.0011; [B]пр = [B]доп = 0.1010; V = [A]доп·24.
Ответ: A×B = -130
Слайд 83Множимое произвольного знака, множитель отрицательный.
Пример. Умножить два целых числа со знаком
Решение. Умножение будем выполнять по четвертому методу.
[A]пр = [A]доп = 0.1101; [B]доп = 1.0110; V = [A]пр·24.
Величина коррекции -A·24 = [-A]доп·24 = 1.0011·24.
Ответ: A×B = -130.
Слайд 84Алгоритм Бута.
В основе алгоритма Бута лежит следующее соотношение, характерное для
2m + 2m-1 + … + 2k = 2m+1 – 2k,
где m и k – номера крайних разрядов в группе из последовательных единиц. Например, 011110 = 25 - 21. Это означает, что при наличии в множителе групп из нескольких единиц (комбинаций вида 011110), последовательное добавление к СЧП множимого с нарастающим весом (от 2k до 2m) можно заменить вычитанием из СЧП множимого с весом 2k и прибавлением к СЧП множимого с весом 2m+1.
Слайд 85Реализация алгоритма предполагает последовательный в направлении справа налево анализ пар разрядов
Комбинация 10 означает начало цепочки последовательных единиц, и в этом случае производится вычитание множимого из СЧП.
Комбинация 01 соответствует завершению цепочки единиц, и здесь множимое прибавляется к СЧП.
Комбинация 00 свидетельствует об отсутствии цепочки единиц, а 11 – о нахождении внутри такой цепочки. В обоих случаях никакие арифметические операции не производятся.
Алгоритм Бута.
Слайд 86Пример. Умножить два целых числа без знака по алгоритму Бута:
Решение. [-A]доп = 11111010. После перекодирования Мт 0011 приобретает вид 010-1.
Ответ: A×B = 10010.
Слайд 88Пример. Умножить два целых числа со знаком по модифицированному алгоритму Бута:
Решение. [A]пр = [A]доп = 0.0000011010; [-A]доп = 1.1111100110;
[-2A]доп = 1.1111001100;
[B]пр = 0.10010; [B]доп = 1.01110
Слайд 89Деление чисел с фиксированной запятой
Задача сводится к вычислению частного Q и
, S = Z - QD, S < D, где Z – делимое, D – делитель.
Операция выполняется за n итераций и может быть описана следующим образом:
Частное от деления 2n-разрядного числа на n-разрядное может содержать более чем n разрядов. В этом случае возникает переполнение, из-за чего перед выполнением деления необходима проверка условия
Слайд 90Деление с восстановлением остатка и неподвижным делителем
исходное значение частичного остатка полагается
частичный остаток сдвигается на один разряд влево;
из сдвинутого ЧО вычитается делитель и анализируется знак результата вычитания;
очередной разряд частного равен единице, когда результат вычитания положителен, и нулю, если отрицателен. В последнем случае значение остатка восстанавливается до того значения, которое было до вычитания;
пункты 2-4 последовательно выполняются для получения всех разрядов частного.
В общем случае для определения (n-i)-й цифры частного анализируется частичный остаток. Если ЧОi-1 ≥ 0, он сдвигается влево и из него далее вычитается Дт, в результате чего получается остаток ЧОi. Если же ЧОi-1 < 0, то сначала восстанавливается предыдущий положительный (сдвинутый) остаток, для чего к ЧОi-1 прибавляется Дт. Далее восстановленный остаток сдвигается влево, из него вычитается Дт, и в результате получается остаток ЧОi. При ЧОi ≥ 0 (n-i)-я цифра частного равна единице, при ЧОi <. 0 – нулю.
Слайд 91Пример. Разделить с восстановлением остатка Дм A = 41 на Дт
Решение. A = 00101001; B = 0111; [-B]доп = 1.1001
Слайд 92Пример. Разделить без восстановления остатка Дм A = 41 на Дт
Решение. A = 00101001; B = 0111; [-B]доп = 1.1001
Слайд 94Временные диаграммы переключения инвертирующего логического элемента
Усредненное значение задержки распространения сигнала
Слайд 95Схема логических выходов элементов ТТЛ
Особенность таких выходов состоит в том, что
Слайд 100Функционирование дешифратора описывается системой конъюнкций:
При ЕN = 1 дешифратор работает как
Слайд 105Мультиплексор
Двоичный код, поступающий на адресные входы, определяет (выбирает) один из информационных
Работу мультиплексора можно упрощенно представить с помощью
многопозиционного ключа.
Слайд 106 Работа мультиплексора описывается соотношением
Мультиплексор «четыре в один».
При отсутствии разрешения работы
Слайд 107Пирамидальная схема, выполняющая функции мультиплексора «32-1» и построенная на мультиплексорах меньшей
Слайд 108Демультиплексор
Функционирование демультиплексора, имеющего n = 4 информационных выходов у0, у1,
Слайд 110Совместное использование мультиплексора и демультиплексора для передачи данных от n источников
Слайд 111Функции, вырабатываемые компараторами, определяются следующим образом: они принимают единичное значение (истинны),
Компараторы
и принимает нулевое значение при
Основными отношениями считаются два – «равно» и «больше». Остальные отношения выражаются через них следующим образом:
Компараторы строятся на основе поразрядных операций над одноименными разрядами обоих слов. Слова равны, если попарно равны все одноименные их разряды. Признак (условие) равенства i-х разрядов сравниваемых слов А и В формируется следующим образом:
Условие неравенства i-x разрядов:
Слайд 115Сумматоры
Сумматор – операционный узел, выполняющий арифметическое сложение кодов двух чисел.
Полусумматор имеет
P = ab
Обозначением полусумматора служат буквы HS (half sum – полусумма).
Слайд 116Полный одноразрядный двоичный сумматор имеет три входа: a, b для двух
Уравнения, описывающие работу полного двоичного сумматора, представленные в совершенной дизъюнктивной нормальной форме (СДНФ), имеют вид:
Уравнение для переноса может быть минимизировано:
P = ab + ap + bp
Слайд 117Уравнения можно преобразовать следующим образом
Выражение для S можно записать также в
S = a ⊕ b ⊕ p
Слайд 119Паралельный перенос в i - том разряде многоразрядного сумматора можно определить
Di - функция генерации переноса в данном разряде.
Fi - функция распространения переноса через данный разряд
Pi = ai bi + pi (ai + bi) = Di + pi Fi
D/0 - функция генерации выходного переноса из четырехразрядной секции.
F/0 - функция распространения переноса через четырехразрядную секцию.
Слайд 120По приведенным уравнениям можно реализовать схему ускоренного переноса (СУП) для четырех
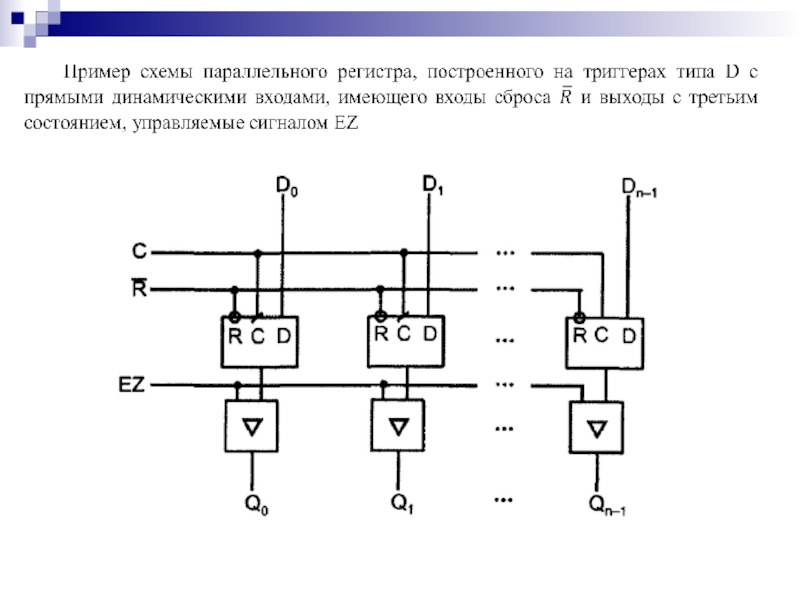
Слайд 140Регистр сдвига представляет собой ряд последовательно соединенных триггеров, число которых определяется
а
б
в
Слайд 148Счетчики с групповой структурой
tуст = ta(k - 1) + tгр,
k –
Слайд 163Реализация технологии 2n-Prefetch при операции чтения данных
Реализация технологии 2n-Prefetch при операции
Слайд 169Абстрактный цифровой автомат
Математической моделью систем с памятью является абстрактный автомат, определяемый
A={a0,a1, …, am} – множество состояний (алфавит состояний), содержащее не менее двух элементов;
Z={z1,z2, …, zF} – множество входных сигналов (входной алфавит), F>1;
W={w1,w2, …, wG} – множество выходных сигналов (выходной алфавит), G>1;
d - функция переходов, реализующая отображение пары “состояние – входной сигнал” в некоторое состояние автомата, т.е. d(ai,zj)=as;
l -функция выходов;
а0 – начальное состояние автомата.
Слайд 171Отмеченная таблица переходов автомата Мура
Граф автомата Мили, описанный ранее табличным способом
Слайд 173Структурный синтез частичного цифрового автомата
Кодирование входных, выходных сигналов и внутренних
Слайд 184Расширенная таблица переходов-выходов
am – исходное состояние,
as – состояние перехода,
X(am, as)
Y(am, as) – выходные сигналы (микрооперации) на переходе МПА из состояния am в состояние as,
h – номер строки (перехода).