- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Трассировка лучей презентация
Содержание
- 1. Трассировка лучей
- 2. Необходимые пояснения Представляет собой метод решения полного
- 3. Ряд Неймана Физически ряд Неймана представляет разложение
- 4. Геометрическая интерпретация ряда Неймана Оба метода имеют
- 5. Координаты луча Следующий этап – определение точки
- 6. Пересечения луча с поверхностью Аналогично можно найти
- 7. Пересечение с гранью Количество граней для аппроксимации
- 8. Преломление луча на поверхности раздела Позволяет по
- 9. Параксиальное приближение Соответствует формуле Гаусса (Gauβ)
- 10. Стохастическая рекурсия лучей Наилучший метод решения задачи стохастической рекурсии – метод Монте-Карло
Слайд 1Трассировка лучей
☎: +7 (095) 763-5239 BudakVP@mpei.ru
Будак Владимир Павлович,
НИУ «МЭИ»
кафедра светотехники
Слайд 2Необходимые пояснения
Представляет собой метод решения полного уравнения глобального освещения
В литературе по
Медведев В.Е., Парицкая Г.Г. Расчет освещенности в изображении // Оптика и спектроскопия, 1966. Т.22, N5. - С.638-642.
Кущ О.К., Митин А.И. Расчет светораспределения зеркальных симметричных поверхностей с протяженным источником света на ЭВМ //Светотехника, 1976. N6. - С.3-5. Коробко А.А., Кущ О.К. Использование метода Монте-Карло в светотехничес-ких расчетах // Светотехника,1986. N10.-С.14-17. Кущ О.К. Оптический расчет световых и облучательных приборов на ЭВМ.- М.: Энергоатомиздат, 1991. - 150С.
Программа энергетического расчета TracePro
Слайд 3Ряд Неймана
Физически ряд Неймана представляет разложение яркости по кратностям переотражений от
Для простоты дальнейших рассуждений представим уравнение в виде
Если норма ядра |Λ|≤1, то решение интегрального уравнения в выбранном пространстве представимо в виде ряда Неймана
Слайд 4Геометрическая интерпретация ряда Неймана
Оба метода имеют свои достоинства и недостатки, но
Построение луча возможно двумя способами:
от источника к камере – прямой ход
от камеры к источнику – обратный ход
Слайд 5Координаты луча
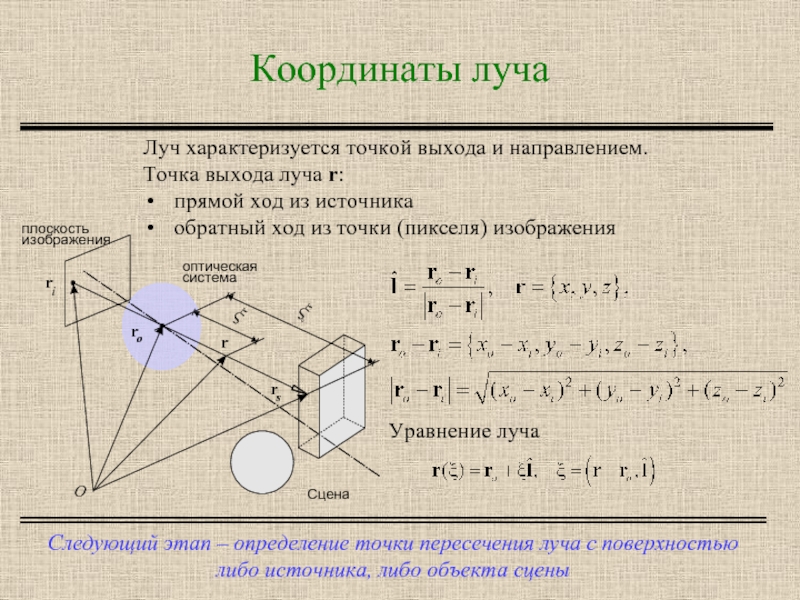
Следующий этап – определение точки пересечения луча с поверхностью либо
Луч характеризуется точкой выхода и направлением.
Точка выхода луча r:
прямой ход из источника
обратный ход из точки (пикселя) изображения
Уравнение луча
Слайд 6Пересечения луча с поверхностью
Аналогично можно найти пересечения с простыми объектами, для
Если поверхность задается уравнением F(r)=0, то координаты точки пересечения есть решение системы уравнений
Пример №1: пересечение с плоскостью
Пример №2: пересечение со сферой
Слайд 7Пересечение с гранью
Количество граней для аппроксимации реальных объектов огромно – применяются
определяется координата пересечения луча с плоскостью многоугольника
определение принадлежности точки пересечения области многоугольника
задача легко из трехмерной сводится к плоской:
если точка пересечения лежит внутри любой из ортогональных проекций многоугольника, то она лежит внутри и самого многоугольника
Исключением из правила является случай: проекция многоугольника вырождается в отрезок - необходимо три подпрограммы для трех проекций
Проверка принадлежности может основываться на вычислении суммы углов между прямыми линиями, проведенными из проверяемой точки ко всем вершинам многоугольника
Если сумма равна 0 - точка внешняя, если ±2π - точка внутри многоугольника.
Диск: принадлежность определяется простым сравнением расстояния от нее до центра
Слайд 8Преломление луча на поверхности раздела
Позволяет по координатам луча сразу получать координаты
Закон преломления Снеллиуса (Снелль Виллеброрд, Snellius, Snell van Royen 1580, Лейден, - 30.10.1626, там же),
Поскольку все три вектора l1, l2 и N лежат в одной плоскости (компланарны)
Слайд 9Параксиальное приближение
Соответствует формуле Гаусса (Gauβ) в отрезках для преломляющей сферической
В приближении параксиальной оптики (N,l)≈1 спроецируем уравнение на плоскость перпендикулярную оптической оси: