- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория рефлексивных игр презентация
Содержание
- 1. Теория рефлексивных игр
- 2. 1. Модели принятия решений. Природная и
- 3. МОДЕЛИ ПРИНЯТИЯ РЕШЕНИЙ В УСЛОВИЯХ ПОЛНОЙ ИНФОРМИРОВАННОСТИ
- 4. ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ ПРИРОДНОЙ НЕОПРЕДЕЛЕННОСТИ
- 5. ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ ИГРОВОЙ НЕОПРЕДЕЛЕННОСТИ
- 6. РАВНОВЕСИЯ В НЕКООПЕРАТИВНЫХ ИГРАХ
- 7. Игра в нормальной форме: Г0 = {N, (Xi)i ∈ N, (fi(⋅))i ∈ N}
- 8. ИГРЫ И ИНФОРМИРОВАННОСТЬ
- 9. МОДЕЛИ КОЛЛЕКТИВНОГО ПОВЕДЕНИЯ
- 10. «РЕФЛЕКСИЯ (лат. reflexio – обращение назад). Термин,
- 11. Рефлексивной является игра, в которой
- 12. ПРИНЯТИЕ РЕШЕНИЙ (ИНФОРМАЦИОННАЯ И СТРАТЕГИЧЕСКАЯ РЕФЛЕКСИЯ)
- 13. СТРАТЕГИЧЕСКАЯ РЕФЛЕКСИЯ: РЕФЛЕКСИВНЫЕ РАЗБИЕНИЯ
- 14. КЛАССИФИКАЦИЯ МОДЕЛЕЙ СТРАТЕГИЧЕСКОЙ РЕФЛЕКСИИ
- 15. СТРАТЕГИЧЕСКАЯ РЕФЛЕКСИЯ (БИМАТРИЧНЫЕ ИГРЫ)
- 16. СТРАТЕГИЧЕСКАЯ РЕФЛЕКСИЯ В БИМАТРИЧНЫХ ИГРАХ
- 17. СТРАТЕГИЧЕСКАЯ РЕФЛЕКСИЯ (ИНФОРМАЦИОННЫЕ ОГРАНИЧЕНИЯ)
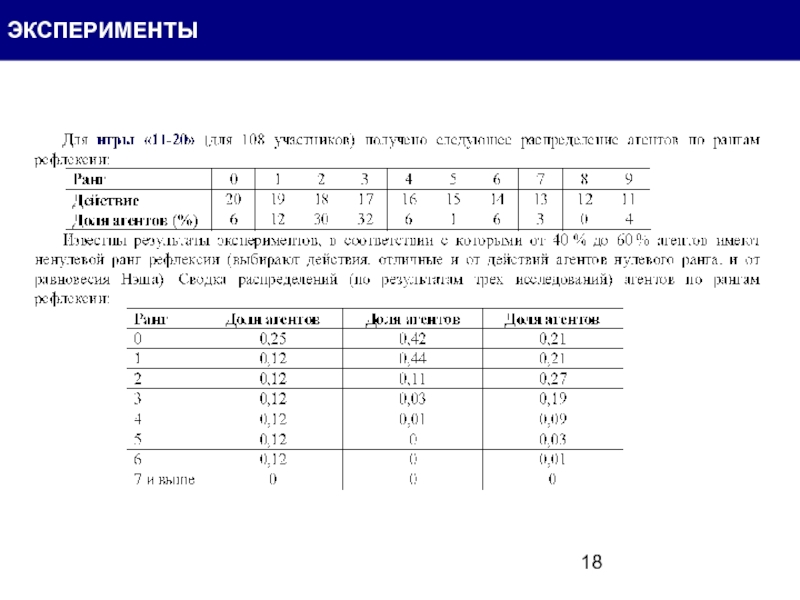
- 18. ЭКСПЕРИМЕНТЫ
- 19. Реализация равновесия Нэша Реализация точки Парето ПРИМЕР СТРАТЕГИЧЕСКОЙ РЕФЛЕКСИИ В ОЛИГОПОЛИИ КУРНО
- 20. Ii - реальный агент Iij
- 21. Набор действий xτ*, τ ∈ Σ+, назовем информационным равновесием,
- 22. xi ≥ 0, i ∈ N = {1, 2, 3}; θ ∈ Ω = {1, 2} . Пример 1. Пусть первые
- 23. xi ≥ 0, i ∈ N = {1, 2, 3}; θ ∈ Ω = {1, 2} . Пример 2. Пусть первые
- 24. xi ≥ 0, i ∈ N = {1, 2, 3}; θ ∈ Ω = {1, 2}. Пусть все
- 25. Пример (“Детектив”). Пусть имеются следователь и преступник.
- 26. В фильме “Император и убийца” (1999, режиссер
- 27. Утверждение. Если информационное равновесие xτ*, τ ∈ Σ+, существует,
- 28. θ ∈ Ω, xi ∈ Xi, i=1, 2 I1=(θ1, θ12, θ121,…)
- 29. ГI = {N, (Xi)i ∈ N, (fi(⋅))i ∈ N , Ω, I} – рефлексивная игра
- 30. Пусть набор действий xτi, τi ∈ Σ+, является стабильным
- 31. wi (θ, x1,…, xn) = (x1,…, xn) А1. Для любых i ∈ N, σ ∈ Σ, любых
- 32. wi (ri, x1,…, xn) = (x1,…, xn) x* = (x1*,…, xn*) – стабильно-равновесный вектор
- 33. Модель организационной системы определяется
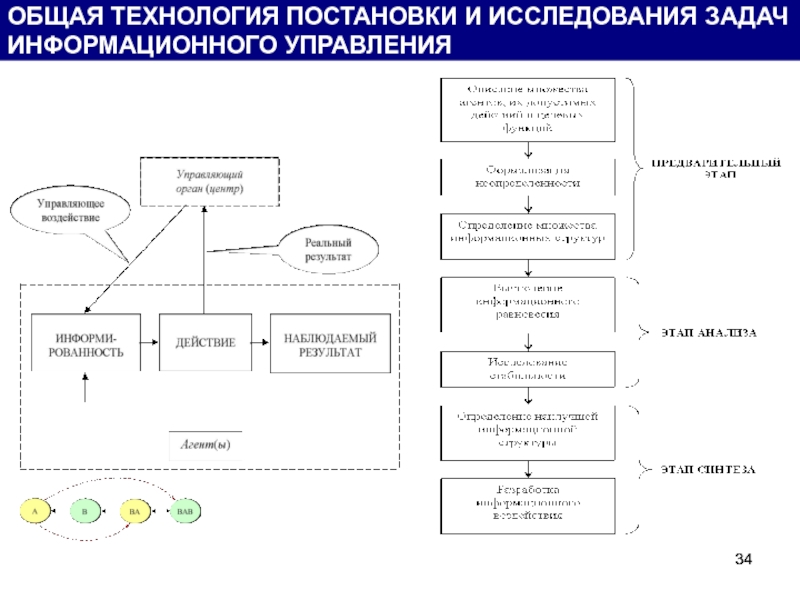
- 34. ОБЩАЯ ТЕХНОЛОГИЯ ПОСТАНОВКИ И ИССЛЕДОВАНИЯ ЗАДАЧ ИНФОРМАЦИОННОГО УПРАВЛЕНИЯ
- 35. Информационное равновесие Задача информационного управления ΨX (I) ⊆ X'
- 36. ИНФОРМАЦИОННОЕ РЕГУЛИРОВАНИЕ И РЕФЛЕКСИВНОЕ УПРАВЛЕНИЕ + Активный прогноз и др.
- 37. EN (θ1,…,θn) = {(x1,…,xn) ∈ X'
- 38. Рефлексивное отображение i–го агента называется стационарным,
- 39. fi(θ, x1, x2) = xi – xi2/ 2 (θ + α xj) α ∈ (0; 1), xi ≥ 0, i = 1, 2 Ω = [0; 1] РЕФЛЕКСИВНЫЕ ОТОБРАЖЕНИЯ. ПРИМЕР 1 (СТАЦИОНАРНЫЕ ОТОБРАЖЕНИЯ)
- 40. f1(θ, x1, x2) = θ (1 – x2) x1 –x12 /2, f2(θ, x1, x2) = θ x1 x2 –x22 /2 Ω = [1/2 ;1], X1 = X2 = (0;1) РЕФЛЕКСИВНЫЕ ОТОБРАЖЕНИЯ. ПРИМЕР 2 (НЕСТАЦИОНАРНЫЕ ОТОБРАЖЕНИЯ)
- 42. РЕФЛЕКСИЯ И ХАОС
- 43. Механизм: i-й агент ( i ∈ N
- 44. EN – множество наборов типов, для
- 45. Пример манипулируемого, но рефлексивно неманипулируемого механизма: два
- 46. 1. Корпоративное управление 1.1. Производитель и посредник* 1.2. Совместное производство*
- 47. 1. Производитель и посредник 2. Совместное
- 48. Команда – коллектив, способный достигать цели автономно
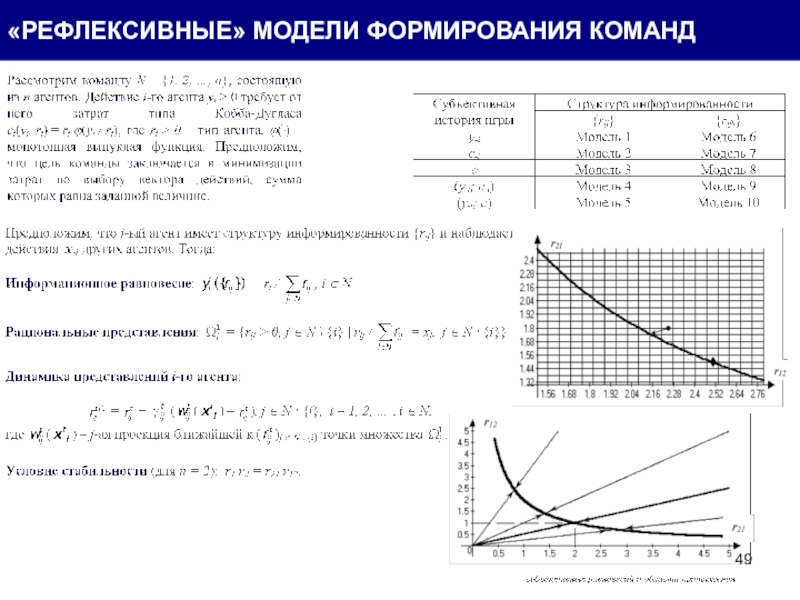
- 49. «РЕФЛЕКСИВНЫЕ» МОДЕЛИ ФОРМИРОВАНИЯ КОМАНД
- 50. n агентов осуществляют совместную деятельность xi ≥
- 51. Отрезок AC – множество равновесий
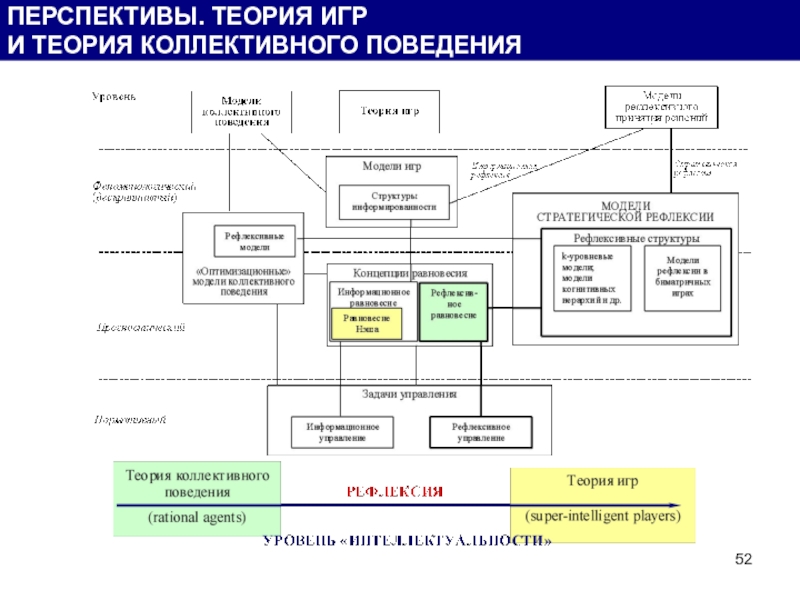
- 52. ПЕРСПЕКТИВЫ. ТЕОРИЯ ИГР И ТЕОРИЯ КОЛЛЕКТИВНОГО ПОВЕДЕНИЯ
- 53. ТЕНДЕНЦИИ: Интеграция теории МАС с
- 54. ЛИТЕРАТУРА www.mtas.ru
Слайд 1ТЕОРИЯ РЕФЛЕКСИВНЫХ ИГР
ТЕОРИЯ РЕФЛЕКСИВНЫХ ИГР
Новиков Дмитрий Александрович
dan@ipu.ru, www.ipu.ru, www.mtas.ru
ИПУ РАН
МФТИ
Слайд 2
1. Модели принятия решений. Природная и игровая неопределенность. Роль информированности. Общее
2. Рефлексия.
3. Стратегическая рефлексия. Рефлексивные разбиения. Максимальный целесообразный ранг рефлексии. Примеры.
4. Информационная рефлексия. Структуры информированности. Информационное равновесие. Примеры.
5. Стабильность и истинность информационного равновесия.
6. Задачи информационного управления.
7. Рефлексивные отображения.
8. Рефлексивная неманипулируемость
9. Примеры.
10. Перспективы
11. Литература.
ПЛАН
Слайд 7Игра в нормальной форме: Г0 = {N, (Xi)i ∈ N, (fi(⋅))i ∈ N} N - множество игроков (агентов), (Xi)i ∈ N
Общее знание (common knowledge – D. Lewis (1969), R. Aumann (1976)) - факт, который:
i) известен всем агентам
ii)всем агентам известно i)
iii) всем агентам известно ii)
и т.д. до бесконечности.
РОЛЬ ИНФОРМИРОВАННОСТИ. ОБЩЕЕ ЗНАНИЕ
Слайд 10«РЕФЛЕКСИЯ (лат. reflexio – обращение назад). Термин, означающий отражение, а также
Рефлексия первого рода (авторефлексия) и второго рода.
Примеры: «Задача о скоординированной атаке», «Electronic Mail Game», «Задача о двух брокерах», … .
Максимальный ранг рефлексии, который следует иметь агенту для того, чтобы охватить все многообразие исходов игры (упуская из виду некоторые стратегии оппонента, агент рискует уменьшить свой выигрыш), назовем максимальным целесообразным рангом рефлексии.
РЕФЛЕКСИЯ
Слайд 11
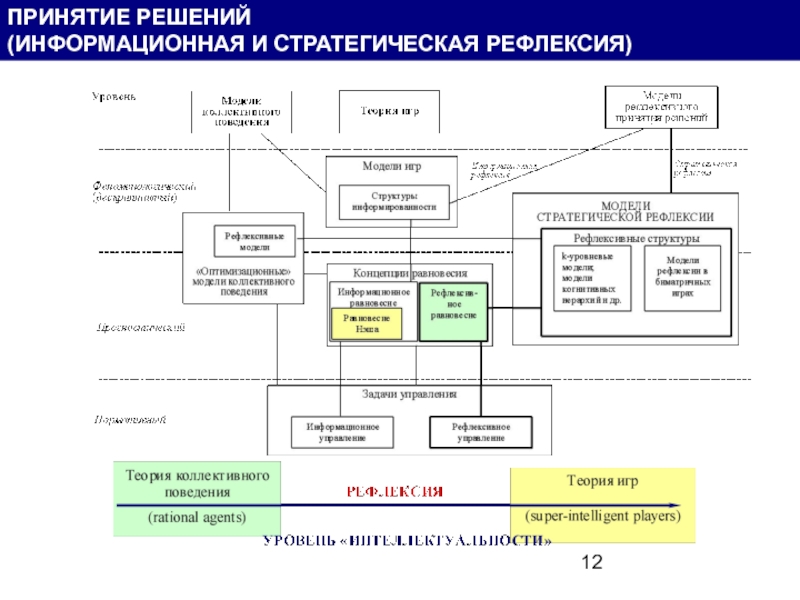
Рефлексивной является игра, в которой информированность игроков не является общим знанием.
Информационная рефлексия – процесс и результат размышлений игрока о том, каковы значения неопределенных параметров, что об этих значениях знают и думают его оппоненты (другие игроки). При этом собственно «игровая» компонента отсутствует, так как никаких решений игрок не принимает.
Иными словами, информационная рефлексия относится к информированности агента о природной реальности (какова игра), и о рефлексивной реальности (какой видят игру другие).
Информационная рефлексия логически предшествует рефлексии несколько иного рода – стратегической рефлексии.
Стратегическая рефлексия – процесс и результат размышлений игрока о том, какие принципы принятия решений используют его оппоненты (другие игроки) в рамках той информированности, которую он им приписывает в результате информационной рефлексии.
Таким образом, информационная рефлексия имеет место только в условиях неполной информированности, и ее результат используется при принятии решений (в том числе – при стратегической рефлексии). Стратегическая рефлексия имеет место даже в случае полной информированности, предваряя принятие игроком решения о выборе действия. Другими словами, информационная и стратегическая рефлексии могут изучаться независимо, однако в условиях неполной информированности обе они имеют место.
ИНФОРМАЦИОННАЯ И СТРАТЕГИЧЕСКАЯ РЕФЛЕКСИЯ
Слайд 19
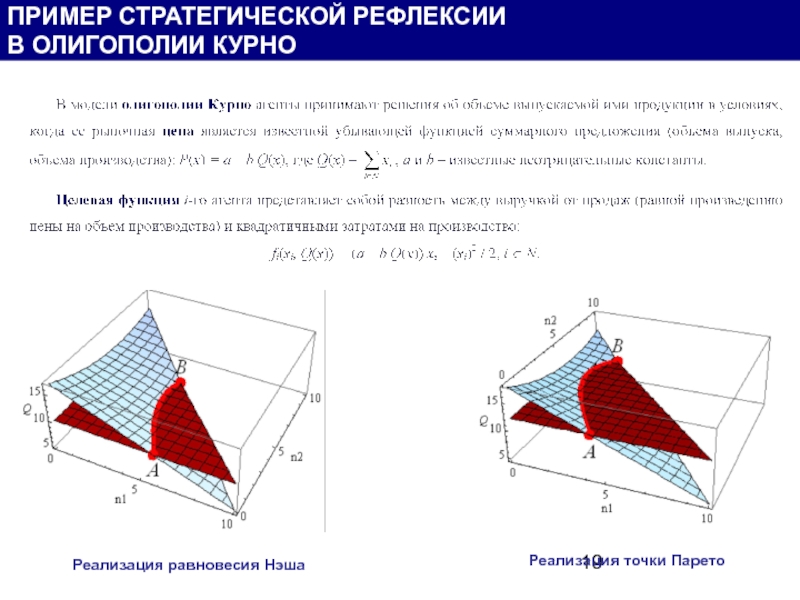
Реализация равновесия Нэша
Реализация точки Парето
ПРИМЕР СТРАТЕГИЧЕСКОЙ РЕФЛЕКСИИ
В ОЛИГОПОЛИИ КУРНО
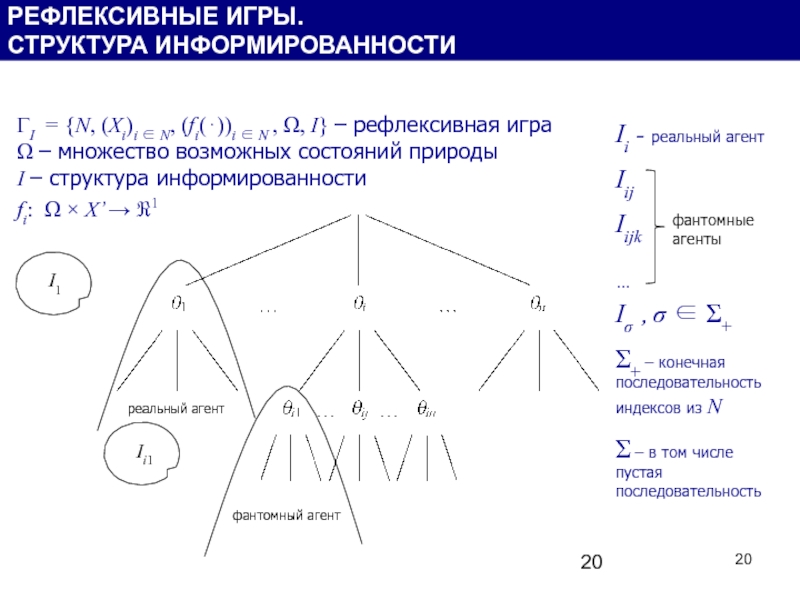
Слайд 20Ii - реальный агент
Iij
Iijk
…
Iσ , σ ∈ Σ+
Σ+
Σ – в том числе пустая последовательность
ГI = {N, (Xi)i ∈ N, (fi(⋅))i ∈ N , Ω, I} – рефлексивная игра
Ω – множество возможных состояний природы
I – структура информированности
fi: Ω × X’ → ℜ1
фантомные агенты
реальный агент
фантомный агент
РЕФЛЕКСИВНЫЕ ИГРЫ.
СТРУКТУРА ИНФОРМИРОВАННОСТИ
Слайд 21Набор действий xτ*, τ ∈ Σ+, назовем информационным равновесием, если выполнены следующие условия:
1. структура
2. ∀i ∈ N, ∀λ,μ ∈ Σ Iλi = Iμi ⇒ xλi* = xμi*;
3. ∀i ∈ N, ∀σ ∈ Σ
(1)
ИНФОРМАЦИОННАЯ РЕФЛЕКСИЯ:
ИНФОРМАЦИОННОЕ РАВНОВЕСИЕ
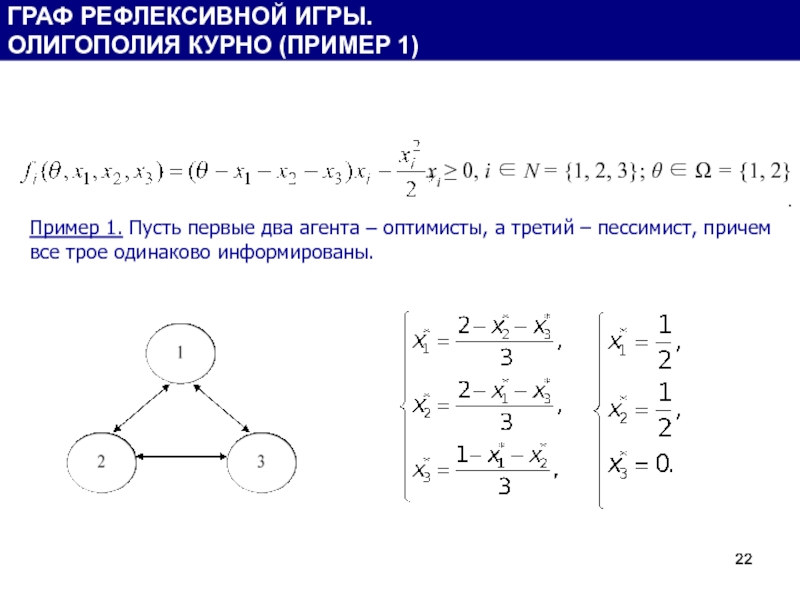
Слайд 22 xi ≥ 0, i ∈ N = {1, 2, 3}; θ ∈ Ω = {1, 2}
.
Пример 1. Пусть первые два агента – оптимисты, а третий
ГРАФ РЕФЛЕКСИВНОЙ ИГРЫ.
ОЛИГОПОЛИЯ КУРНО (ПРИМЕР 1)
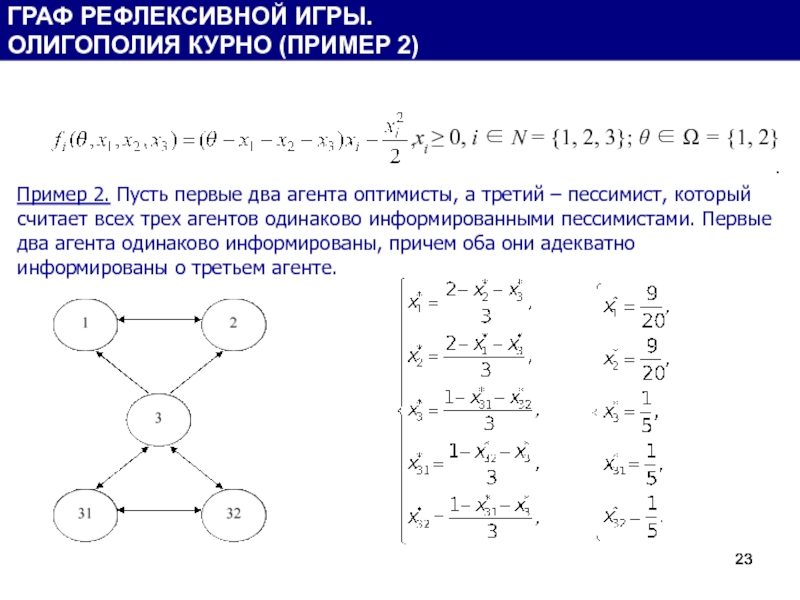
Слайд 23 xi ≥ 0, i ∈ N = {1, 2, 3}; θ ∈ Ω = {1, 2}
.
Пример 2. Пусть первые два агента оптимисты, а третий –
ГРАФ РЕФЛЕКСИВНОЙ ИГРЫ.
ОЛИГОПОЛИЯ КУРНО (ПРИМЕР 2)
Слайд 24
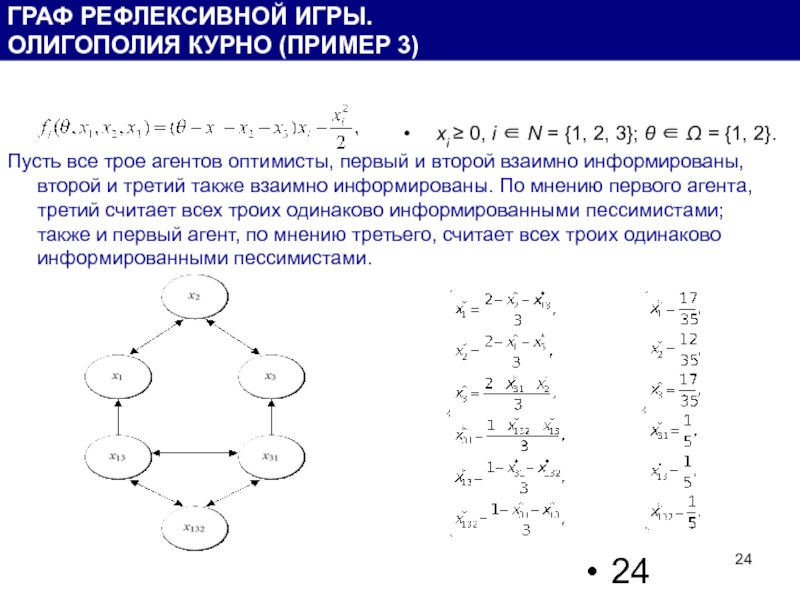
xi ≥ 0, i ∈ N = {1, 2, 3}; θ ∈ Ω = {1, 2}.
Пусть все трое агентов оптимисты, первый и второй
ГРАФ РЕФЛЕКСИВНОЙ ИГРЫ.
ОЛИГОПОЛИЯ КУРНО (ПРИМЕР 3)
Слайд 25
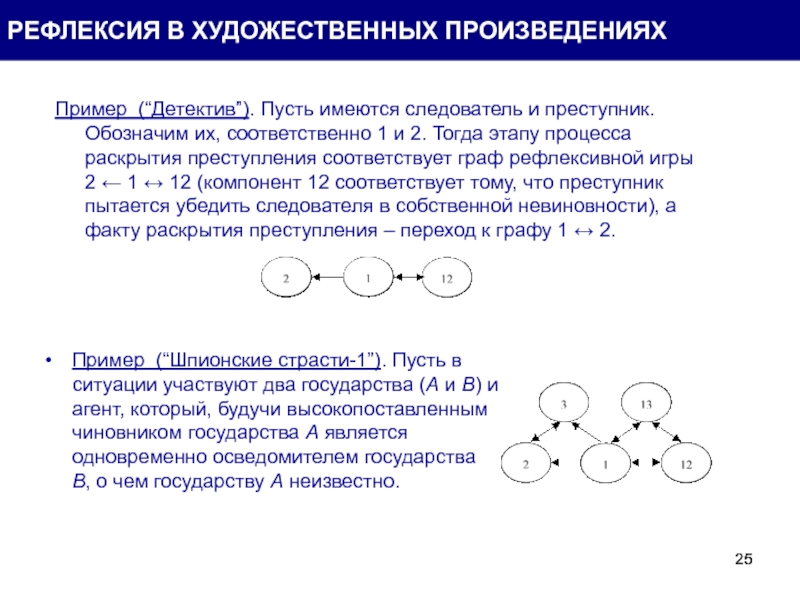
Пример (“Детектив”). Пусть имеются следователь и преступник. Обозначим их, соответственно 1 и 2.
Пример (“Шпионские страсти-1”). Пусть в ситуации участвуют два государства (А и В) и агент, который, будучи высокопоставленным чиновником государства А является одновременно осведомителем государства В, о чем государству А неизвестно.
РЕФЛЕКСИЯ В ХУДОЖЕСТВЕННЫХ ПРОИЗВЕДЕНИЯХ
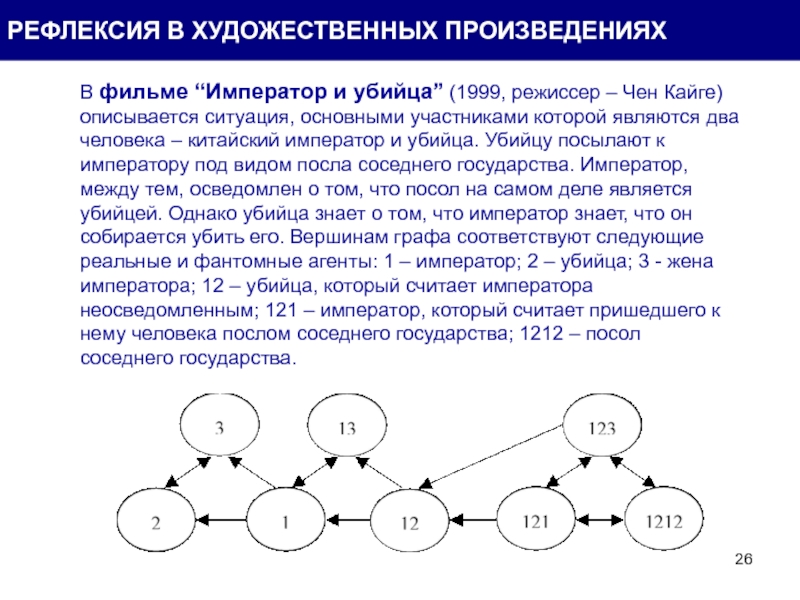
Слайд 26В фильме “Император и убийца” (1999, режиссер – Чен Кайге) описывается
РЕФЛЕКСИЯ В ХУДОЖЕСТВЕННЫХ ПРОИЗВЕДЕНИЯХ
Слайд 27Утверждение. Если информационное равновесие xτ*, τ ∈ Σ+, существует, то оно состоит из
Утверждение. Пусть в рефлексивной игре со структурой информированности конечной сложности множества действий Xi – выпуклые компактные подмножества ℜn, для каждого агента целевая функция fi(θ, x1, …, xn) при любом θ ∈ Ω непрерывна по всем переменным и строго вогнута по переменной xi. Тогда в этой игре существует информационное равновесие.
Утверждение. Пусть для любого непустого множества N’⊆ N справедлив следующий факт: для любых θk ∈ Ω, k ∈ N’, и любых xm*∈ Xm, m ∉ N’, существует равновесие Нэша в игре с общим знанием k-агентов, то есть существуют xk*, k ∈ N’, удовлетворяющие
Тогда для любой конечной регулярной структуры информированности существует информационное равновесие.
СУУЩЕСТВОВАНИЕ ИНФОРМАЦИОННОГО РАВНОВЕСИЯ
Слайд 28θ ∈ Ω, xi ∈ Xi, i=1, 2
I1=(θ1, θ12, θ121,…) I2=(θ2, θ21, θ212, …)
=ϕ(I1)=ϕ(θ1, θ12, θ121, …),
=ψ(I2)=ψ(θ2, θ21, θ212, …).
Утверждение. Пусть в игре (*), в которой для любых θ , x1 , x2 множества (**) непусты, существует хотя бы одно точечное равновесие Байеса–Нэша (***). Тогда для любой структуры информированности бесконечной глубины I1 и любого χ ∈ X1 существует равновесие, в котором χ является равновесным действием первого агента при его структуре информированности I1 .
(*)
(**)
(***)
РЕФЛЕКСИВНЫЕ ИГРЫ И БАЙЕСОВЫ ИГРЫ. ОГРАНИЧЕННОСТЬ РАНГА РЕФЛЕКСИИ
Слайд 29ГI = {N, (Xi)i ∈ N, (fi(⋅))i ∈ N , Ω, I} – рефлексивная игра wi(⋅): Ω × X’ → Wi, i ∈ N wi(⋅) – функция наблюдения
Информационное равновесие xτi, τi∈Σ+, будем называть стабильным при заданной структуре информированности I , если для любого τi∈Σ+ выполняется
(2) wi(θτi, xτi1, …, xτi,i-1, xτi, xτi,i+1, …, xτin) =
= wi(θτ, xτ1, …, xτ,i-1, xτi, xτ,i+1, …, xτn).
СТАБИЛЬНОЕ ИНФОРМАЦИОННОЕ РАВНОВЕСИЕ
Утверждение. Пусть структура информированности I имеет сложность ν и существует информационное равновесие xτi, τi ∈ Σ+. Тогда система соотношений (2) содержит не более чем ν попарно различных условий.
Слайд 30Пусть набор действий xτi, τi ∈ Σ+, является стабильным информационным равновесием. Будем называть
Стабильное информационное равновесие, не являющееся истинным, назовем ложным.
Утверждение. Пусть целевые функции агентов имеют вид
(3) fi (ri, x1, …, xn) = ϕi (ri, xi, yi(x-i)),
а функции наблюдения – вид wi(θ, x) = yi(x-i), i ∈ N . Тогда любое стабильное равновесие является истинным.
Содержательно условие (3) означает следующее: выигрыш каждого агента зависит от его типа, его действия и функции наблюдения, зависящей от действий остальных агентов, но не от их типов.
ИСТИННЫЕ И ЛОЖНЫЕ РАВНОВЕСИЯ
Слайд 31wi (θ, x1,…, xn) = (x1,…, xn)
А1. Для любых i ∈ N, σ ∈ Σ, любых представлений θσi ∈ Ω и θ’σi ∈ Ω таких, что
Выполняется
где
Утверждение. Пусть выполнено предположение А1 и существует информационное равновесие x*. Тогда x* является стабильным информационным равновесием в том и только том случае, если структура информированности имеет глубину 1:
∀ i ∈ N, ∀ σ ∈ Σ θσi = θi .
СЛУЧАЙ НАБЛЮДАЕМЫХ ДЕЙСТВИЙ.
НЕОПРЕДЕЛЕННОСТЬ – СОСТОЯНИЕ ПРИРОДЫ
Слайд 32wi (ri, x1,…, xn) = (x1,…, xn)
x* = (x1*,…, xn*) – стабильно-равновесный вектор действий
Утверждение. Пусть x* – стабильно-равновесный вектор
Утверждение. Если вектор действий реальных агентов x* является стабильно-равновесным при некоторой структуре информированности, то для элементов этой структуры при любых i ∈ N и σ ∈ Σ выполняется rσi ∈ ρi .
СЛУЧАЙ НАБЛЮДАЕМЫХ ДЕЙСТВИЙ.
НЕОПРЕДЕЛЕННОСТЬ – ТИПЫ АГЕНТОВ
Слайд 33
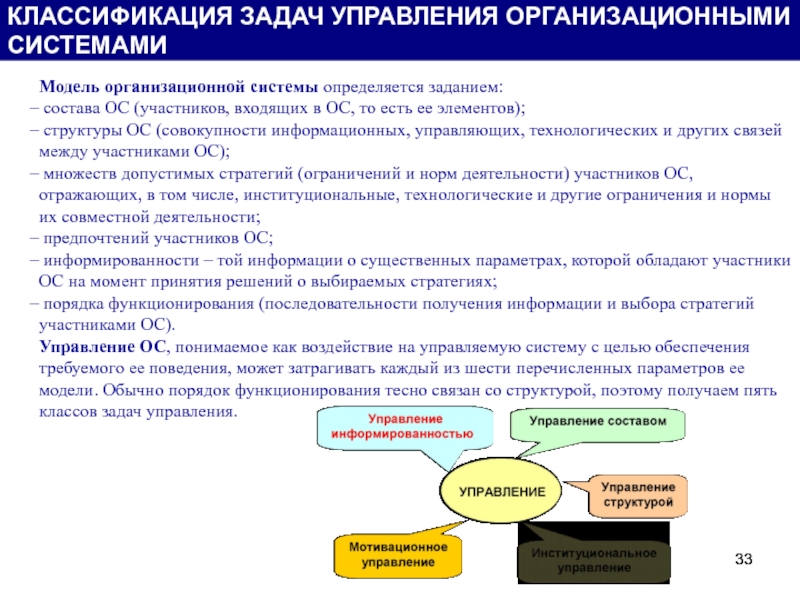
Модель организационной системы определяется заданием:
состава ОС (участников, входящих в ОС,
структуры ОС (совокупности информационных, управляющих, технологических и других связей между участниками ОС);
множеств допустимых стратегий (ограничений и норм деятельности) участников ОС, отражающих, в том числе, институциональные, технологические и другие ограничения и нормы их совместной деятельности;
предпочтений участников ОС;
информированности – той информации о существенных параметрах, которой обладают участники ОС на момент принятия решений о выбираемых стратегиях;
порядка функционирования (последовательности получения информации и выбора стратегий участниками ОС).
Управление ОС, понимаемое как воздействие на управляемую систему с целью обеспечения требуемого ее поведения, может затрагивать каждый из шести перечисленных параметров ее модели. Обычно порядок функционирования тесно связан со структурой, поэтому получаем пять классов задач управления.
КЛАССИФИКАЦИЯ ЗАДАЧ УПРАВЛЕНИЯ ОРГАНИЗАЦИОННЫМИ СИСТЕМАМИ
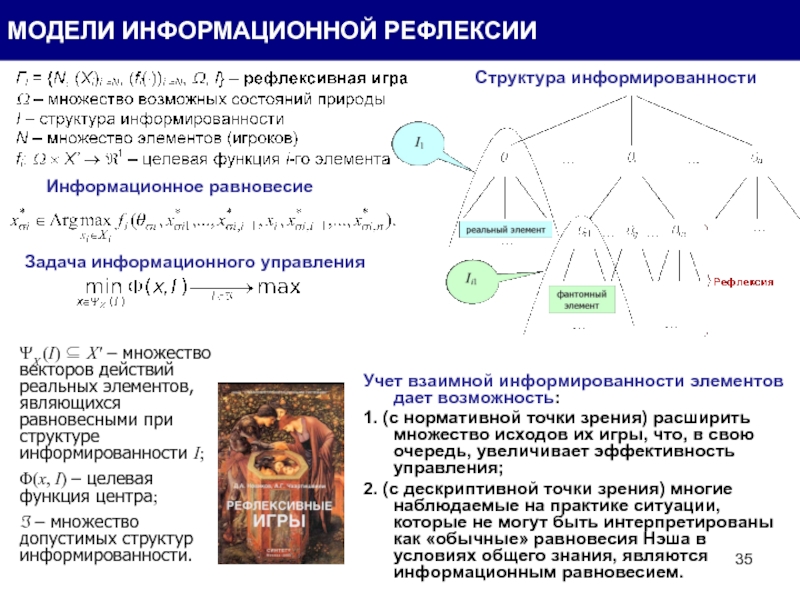
Слайд 35Информационное равновесие
Задача информационного управления
ΨX (I) ⊆ X' – множество векторов действий реальных элементов,
Φ(x, I) – целевая функция центра;
ℑ – множество допустимых структур информированности.
Учет взаимной информированности элементов дает возможность:
1. (с нормативной точки зрения) расширить множество исходов их игры, что, в свою очередь, увеличивает эффективность управления;
2. (с дескриптивной точки зрения) многие наблюдаемые на практике ситуации, которые не могут быть интерпретированы как «обычные» равновесия Нэша в условиях общего знания, являются информационным равновесием.
Структура информированности
МОДЕЛИ ИНФОРМАЦИОННОЙ РЕФЛЕКСИИ
Слайд 37
EN (θ1,…,θn) = {(x1,…,xn) ∈ X' | ∀ i ∈ N
– рефлексивные отображения
Утверждение. Для любых k = 0, 1, … и i ∈ N выполняется
РЕФЛЕКСИВНЫЕ ОТОБРАЖЕНИЯ
Слайд 38
Рефлексивное отображение i–го агента называется стационарным, если
Утверждение. Если рефлексивные отображения всех агентов
СТАЦИОНАРНОСТЬ РЕФЛЕКСИВНЫХ ОТБРАЖЕНИЙ
Слайд 39fi(θ, x1, x2) = xi – xi2/ 2 (θ + α xj)
α ∈ (0; 1), xi ≥ 0, i = 1, 2
Ω = [0; 1]
РЕФЛЕКСИВНЫЕ ОТОБРАЖЕНИЯ.
ПРИМЕР 1 (СТАЦИОНАРНЫЕ ОТОБРАЖЕНИЯ)
Слайд 40f1(θ, x1, x2) = θ (1 – x2) x1 –x12 /2,
f2(θ, x1, x2) = θ x1 x2 –x22 /2
Ω = [1/2 ;1], X1 = X2 = (0;1)
РЕФЛЕКСИВНЫЕ ОТОБРАЖЕНИЯ.
ПРИМЕР 2 (НЕСТАЦИОНАРНЫЕ ОТОБРАЖЕНИЯ)
Слайд 41
Для любых θ1, θ2 ∈ Ω :
(i)
(ii)
(iii)
(iv)
(v)
Утверждение. Рефлексивные отображения игры (i)-(ii) при
ЛИНЕЙНЫЕ РЕФЛЕКСИВНЫЕ ОТОБРАЖЕНИЯ
Слайд 43Механизм: i-й агент ( i ∈ N ) выбирает сообщение центру
Центр назначает агентам планы xi = hi (s) = hi(s1,…,sn) .
Агенты получают выигрыши fi(xi, ri) .
«Классическая» неманипулируемость (типы агентов являются общим знанием): для любого типа ri равновесной стратегией i-го агента является сообщение si* = ri .
Рефлексивная неманипулируемость: для любого типа ri существует подструктура информированности (riσ ), i ∈ N, σ ∈ Σ+ , такая, что si* = ri .
РЕФЛЕКСИВНАЯ НЕМАНИПУЛИРУЕМОСТЬ
МЕХАНИЗМОВ ПЛАНИРОВАНИЯ
Слайд 44
EN – множество наборов типов, для которых сообщение каждым агентом своего
EN = { r∈ℜn |∀i ∈ N ∀si ∈ ℜ1 fi(hi(r), ri) ≥ fi(hi(r1,…,ri-1, si, ri+1,…,rn), ri) }.
Утверждение. Для того, чтобы механизм планирования являлся рефлексивно неманипулируемым, достаточно, чтобы для любого i-го агента, i ∈ N, существовал набор типов r’ = (r’1, …,r’n ) ∈ EN такой, что выполнено
При этом для реализации рефлексивной неманипулируемости достаточно ограничиться не более чем вторым рангом рефлексии агентов.
РЕФЛЕКСИВНАЯ НЕМАНИПУЛИРУЕМОСТЬ
МЕХАНИЗМОВ ПЛАНИРОВАНИЯ
Слайд 45Пример манипулируемого, но рефлексивно неманипулируемого механизма:
два агента с типами r1 ,
Равновесные по Нэшу стратегии (заявки):
s1* (r1, r2) = 2 (2 r1 + r2)/3, s2* (r1, r2) = 2 (2 r2+ r1)/3 .
Нетрудно видеть, что
si* = ri при riσ = 0, i =1,2, σ ∈ Σ+ .
РЕФЛЕКСИВНАЯ НЕМАНИПУЛИРУЕМОСТЬ
МЕХАНИЗМОВ ПЛАНИРОВАНИЯ
Слайд 461. Корпоративное управление
1.1. Производитель и посредник*
1.2. Совместное производство*
1.3. Конкуренция на рынке*
1.4. Аккордная оплата труда*
1.5. Продавец и покупатель*
1.6. Заказчик
1.7. Активная экспертиза*
1.8. Олигополия Курно**
1.9. Распределение ресурса**
1.10. Страхование*
1.11. Конкурс**
1.12. Формирование команды*
2. Игры поиска*
3. «Принцип дефицита»*
4. Коррупция**
5. Биполярный выбор*
6. Реклама товара*
7. Предвыборная борьба*
* – множество исходов игры расширяется за счет ИУ
** – возможны только истинные стабильные равновесия, при этом представления агентов могут быть ложными
ПРИКЛАДНЫЕ МОДЕЛИ ИНФОРМАЦИОННОГО УПРАВЛЕНИЯ
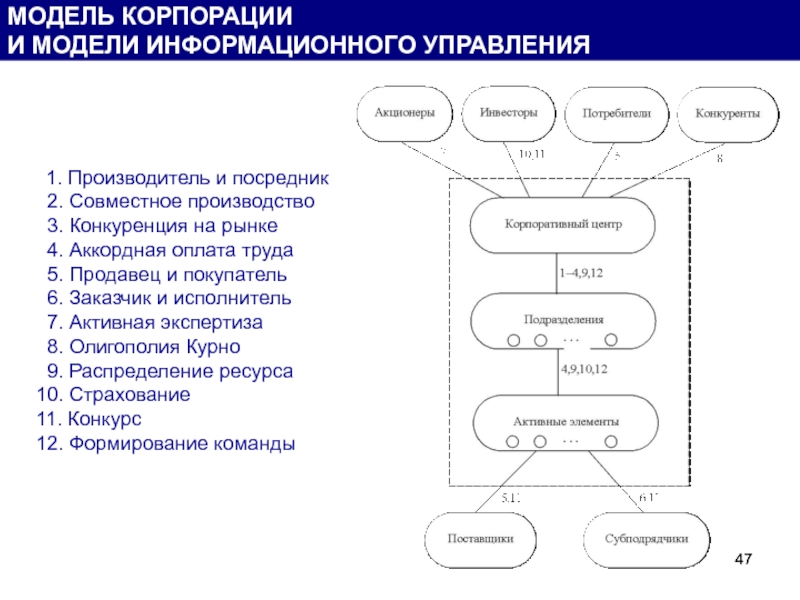
Слайд 47
1. Производитель и посредник
2. Совместное производство
3. Конкуренция на рынке
4. Аккордная оплата
5. Продавец и покупатель
6. Заказчик и исполнитель
7. Активная экспертиза
8. Олигополия Курно
9. Распределение ресурса 10. Страхование
11. Конкурс
12. Формирование команды
МОДЕЛЬ КОРПОРАЦИИ
И МОДЕЛИ ИНФОРМАЦИОННОГО УПРАВЛЕНИЯ
Слайд 48Команда – коллектив, способный достигать цели автономно и согласованно при минимальных
Группа – совокупность людей, объединенных общностью интересов, профессии, деятельности и т.п.
Коллектив – объединение людей, осуществляющих совместную деятельность и обладающих общими интересами.
Организационная система – объединение людей, совместно реализующих некоторую программу или цель и действующих на основе определенных процедур и правил.
Группа, коллектив, организация и команда
Этапы существования команд
ПРИМЕР: КОМАНДЫ
Слайд 50n агентов осуществляют совместную деятельность
xi ≥ 0 – действие i-го агента
θ – суммарное действие агентов, за которое центр выплачивает вознаграждение (иначе не выплачивает ничего)
σi – вознаграждение i-го агента
ci(xi) – затраты агентов (возрастающая функция, ci(0) = 0 )
xi+=max { xi ≥ 0 | ci(xi) ≤ σi }
В результате игры общим знанием среди агентов становится факт выплаты или невыплаты вознаграждения.
Утверждение. Любой набор действий
можно сделать стабильным (и притом единственным) информационным равновесием в рамках структуры информированности глубины 2.
ПРИМЕР: АККОРДНАЯ ОПЛАТА ТРУДА
Слайд 51
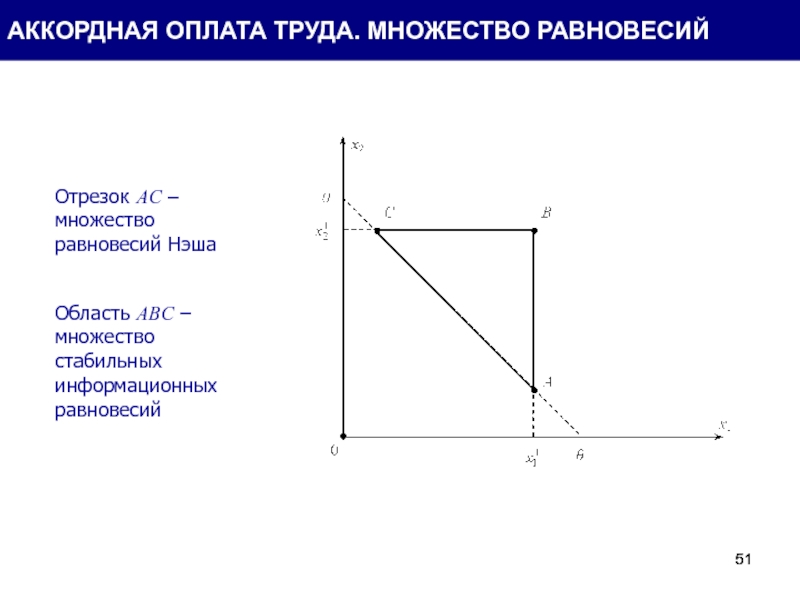
Отрезок AC – множество равновесий Нэша
Область ABC – множество стабильных информационных
АККОРДНАЯ ОПЛАТА ТРУДА. МНОЖЕСТВО РАВНОВЕСИЙ
Слайд 53
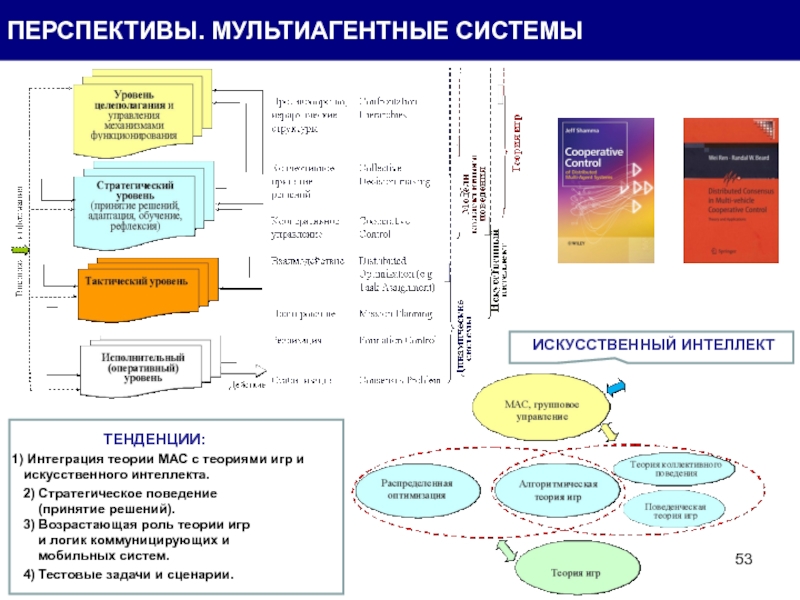
ТЕНДЕНЦИИ:
Интеграция теории МАС с теориями игр и искусственного интеллекта.
2)
3) Возрастающая роль теории игр
и логик коммуницирующих и
мобильных систем.
4) Тестовые задачи и сценарии.
ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ
ПЕРСПЕКТИВЫ. МУЛЬТИАГЕНТНЫЕ СИСТЕМЫ


























![fi(θ, x1, x2) = xi – xi2/ 2 (θ + α xj) α ∈ (0; 1), xi ≥ 0, i = 1, 2 Ω = [0; 1]РЕФЛЕКСИВНЫЕ ОТОБРАЖЕНИЯ. ПРИМЕР 1 (СТАЦИОНАРНЫЕ ОТОБРАЖЕНИЯ)](/img/tmb/2/149741/16df28bac7237d6ef8d86aaa08ba9c62-800x.jpg)
![f1(θ, x1, x2) = θ (1 – x2) x1 –x12 /2, f2(θ, x1, x2) = θ x1 x2 –x22 /2Ω = [1/2 ;1], X1 = X2 = (0;1) РЕФЛЕКСИВНЫЕ ОТОБРАЖЕНИЯ. ПРИМЕР 2 (НЕСТАЦИОНАРНЫЕ ОТОБРАЖЕНИЯ)](/img/tmb/2/149741/82e15c5d40458024f2ed18a9153375bb-800x.jpg)