- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория графов в информатике презентация
Содержание
- 1. Теория графов в информатике
- 2. Содержание Введение Теория графов Классические задачи Графы в информатике Заключение
- 3. Введение
- 4. Графы используют во всех отраслях нашей жизни.
- 5. Теория графов
- 6. Граф – это некоторое конечное множество точек, называемых вершинами,
- 7. Понятия теории графов Степень вершины - число
- 8. Некоторые свойства графов Если все вершины графа
- 9. Некоторые свойства плоских графов Лемма1. Число рёбер
- 10. Классические задачи
- 11. «Жадные алгоритмы» Требуется проложить железную дорогу, соединяющую
- 12. «Жадные алгоритмы»
- 13. Графы в информатике
- 14. Блок-схемы Задача: построить блок-схему попадания
- 15. Решение задач Необходимо указать таблицу, для которой
- 16. Решение задач
- 17. Решение задач A→C→B стоимость 7 A→C→E→B
- 18. Заключение
- 19. На языке теории графов формируются и решаются
Слайд 4Графы используют во всех отраслях нашей жизни. Знание основ теории графов
Графы используют в связи с развитием теории вероятностей, математической логики и информационных технологий.
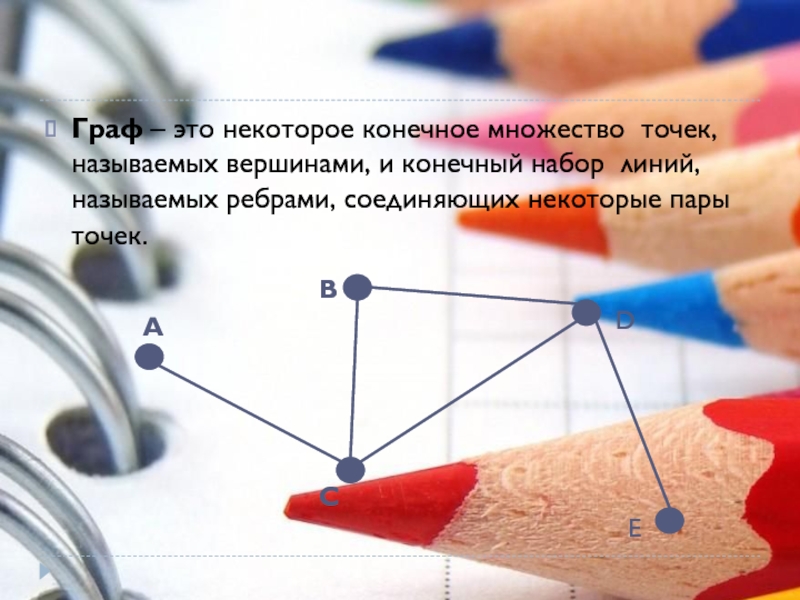
Слайд 6Граф – это некоторое конечное множество точек, называемых вершинами, и конечный набор линий, называемых
А
В
С
D
E
Слайд 7Понятия теории графов
Степень вершины - число рёбер, выходящих из этой вершины.
Граф
Ориентированным (орграфом) называется граф, у которого рёбрам присвоено направление.
Плоский граф – граф, расположенный в одной плоскости, ребра которого не пересекаются.
Полный граф – граф, в котором соединены все вершины всеми возможными способами.
Слайд 8Некоторые свойства графов
Если все вершины графа чётные, то можно одним росчерком
Граф с двумя нечётными вершинами тоже можно начертить одним росчерком.
Граф с более чем двумя нечётными вершинами, невозможно начертить одним росчерком.
Слайд 9Некоторые свойства плоских графов
Лемма1. Число рёбер в графе ровно в 2
Лемма2. Сумма степеней вершин графа чётна.
Лемма3. Число нечётных вершин графа чётно.
Лемма4. Если полный граф имеет n вершин, то количество ребер будет равно
Слайд 11«Жадные алгоритмы»
Требуется проложить железную дорогу, соединяющую несколько городов. Для любой пары
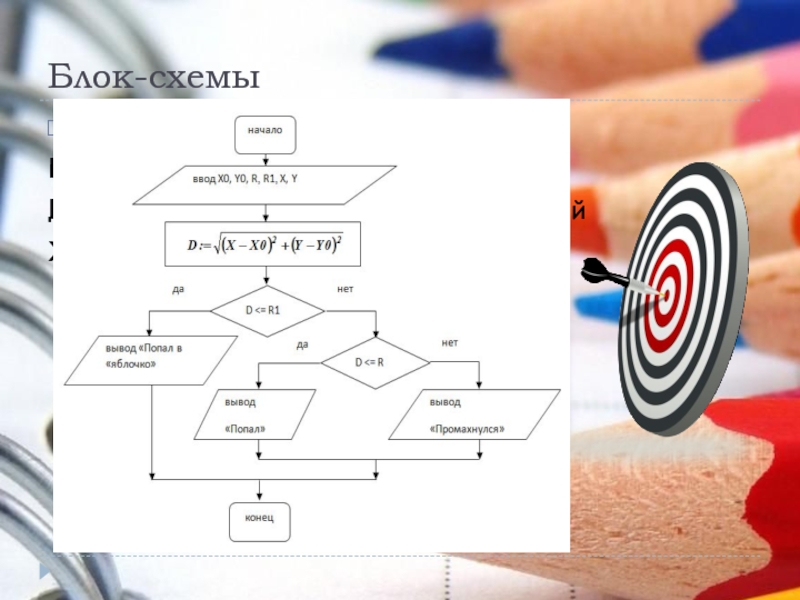
Слайд 14Блок-схемы
Задача:
построить блок-схему попадания
дротика в цель в игре «Дартс»
Решение:
Пусть
R и R1 – радиусы красного и черного полей
X и Y – это координаты стрелы
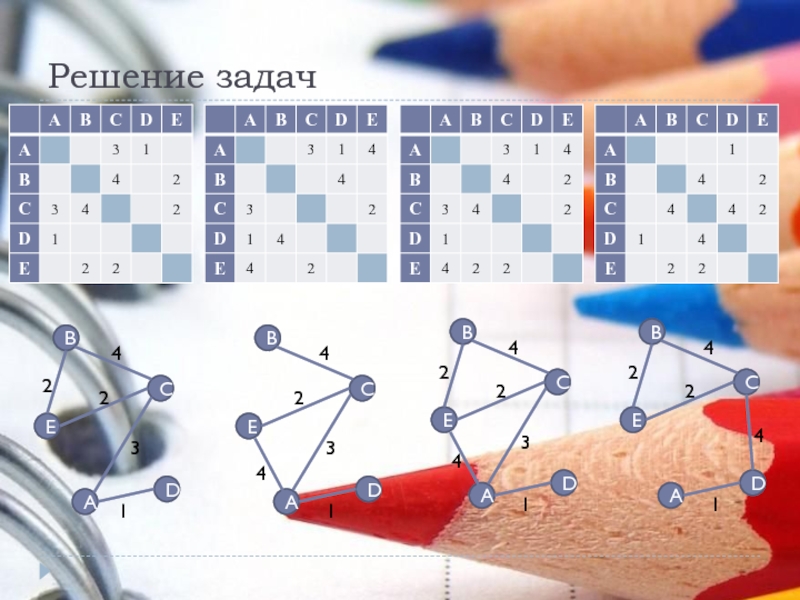
Слайд 15Решение задач
Необходимо указать таблицу, для которой выполняется условие: «Минимальная стоимость прокладки
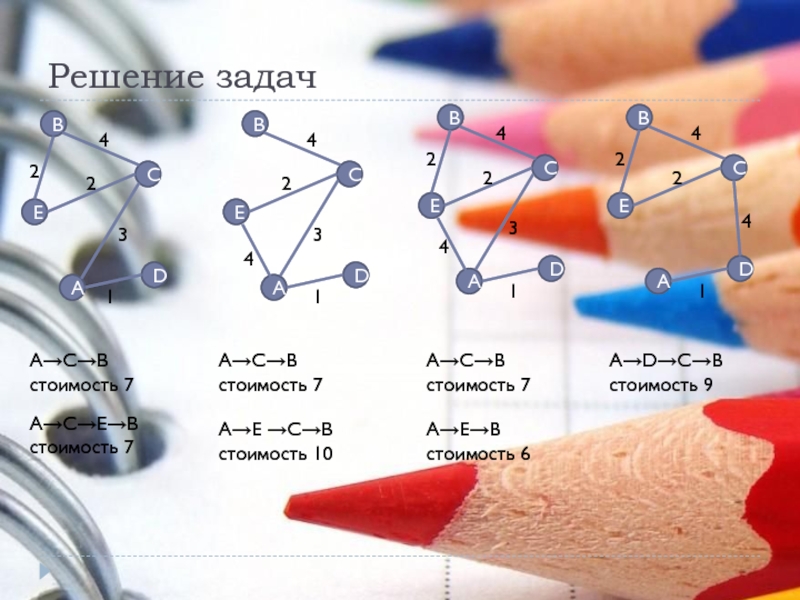
Слайд 17Решение задач
A→C→B стоимость 7
A→C→E→B стоимость 7
A→C→B стоимость 7
A→E →C→B стоимость 10
A→C→B
A→E→B
стоимость 6
A→D→C→B стоимость 9
Слайд 19На языке теории графов формируются и решаются многие технические задачи, задачи
Графы используются для наглядного представления объектов и связи между ними.
Но к теории графов также относится целый ряд проблем, не решенных на сегодняшний день.