- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория графов. Планарные графы презентация
Содержание
- 1. Теория графов. Планарные графы
- 2. При проектировании интегральных микросхем возникает задача построения графа с непересекающимися ребрами.
- 3. ОПРЕДЕЛЕНИЕ Планарным графом называется граф, который может
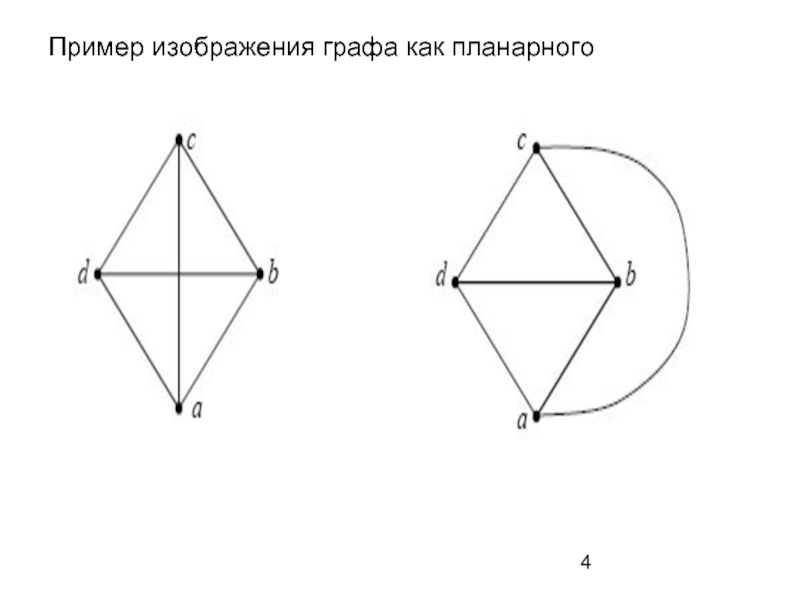
- 4. Пример изображения графа как планарного
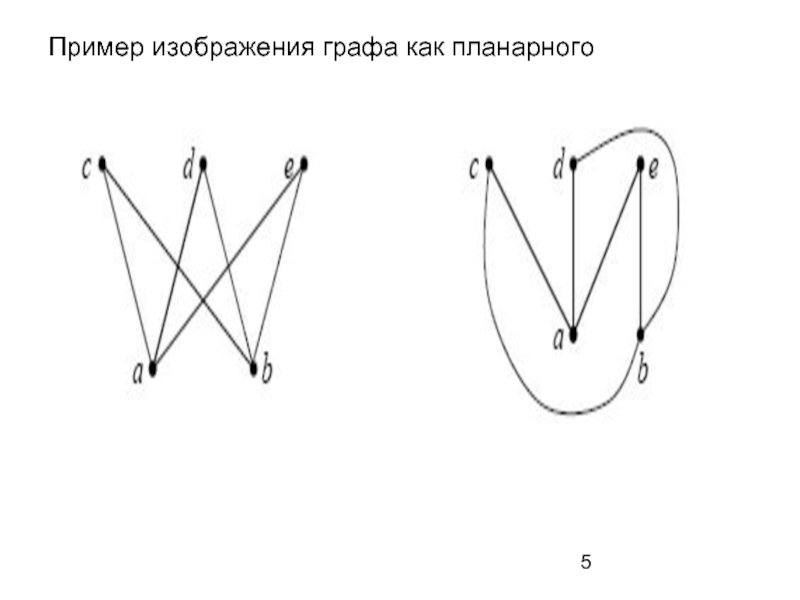
- 5. Пример изображения графа как планарного
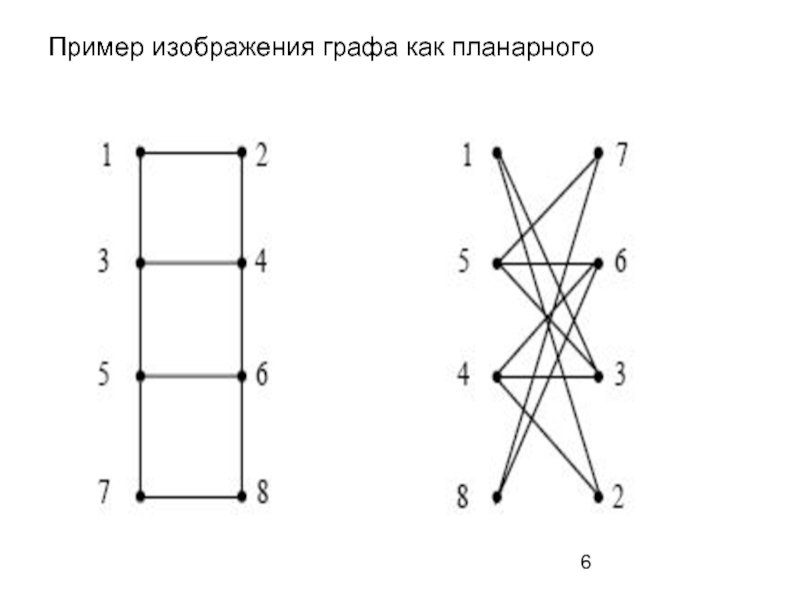
- 6. Пример изображения графа как планарного
- 7. Понятие плоского графа Плоским графом называется граф,
- 8. Граф называется планарным, если он изоморфен некоторому плоскому графу.
- 9. Если граф планарен и нарисован так, что
- 10. Грань планарного графа – максимальный участок плоскости
- 11. Граф G и его планарная укладка. Планарная
- 12. Всегда имеется одна неограниченная внешняя грань,
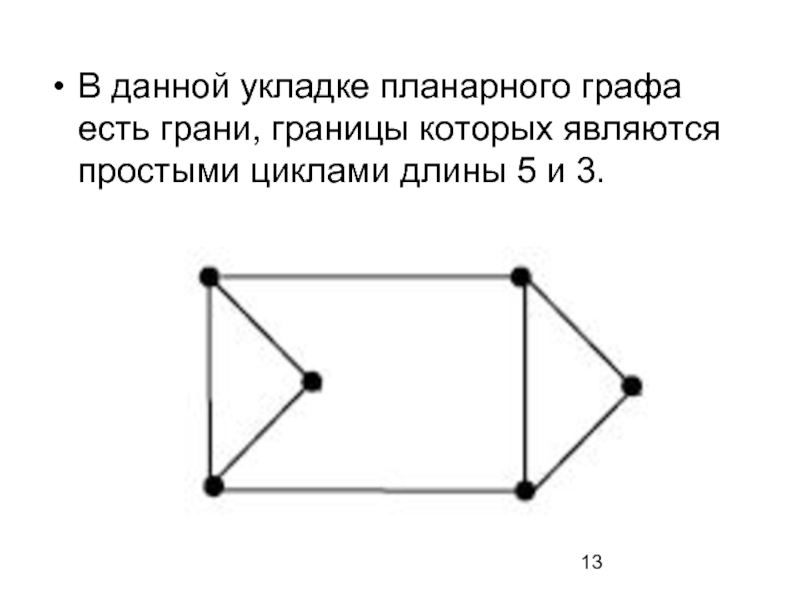
- 13. В данной укладке планарного графа есть грани,
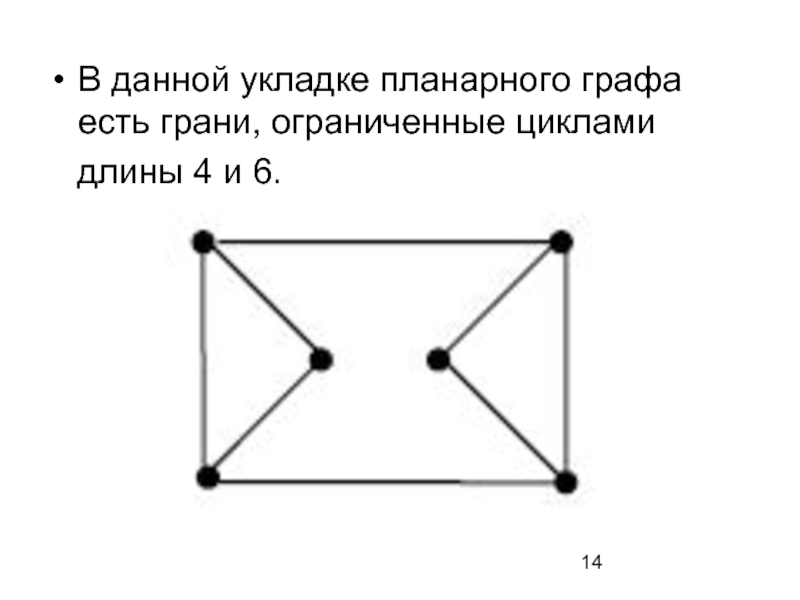
- 14. В данной укладке планарного графа есть грани,
- 15. Теорема Эйлера ТЕОРЕМА. Если G –
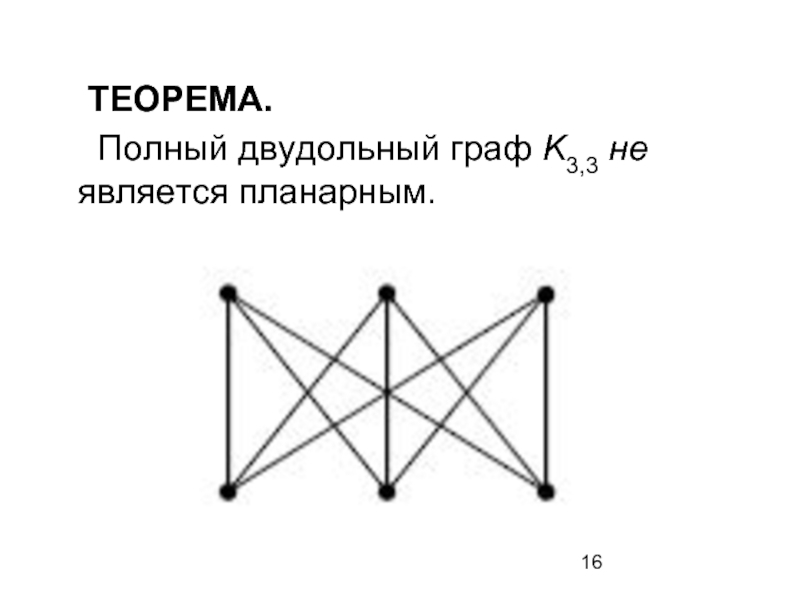
- 16. ТЕОРЕМА. Полный двудольный граф K3,3 не является планарным.
- 17. Лемма. В произвольном связном планарном графе
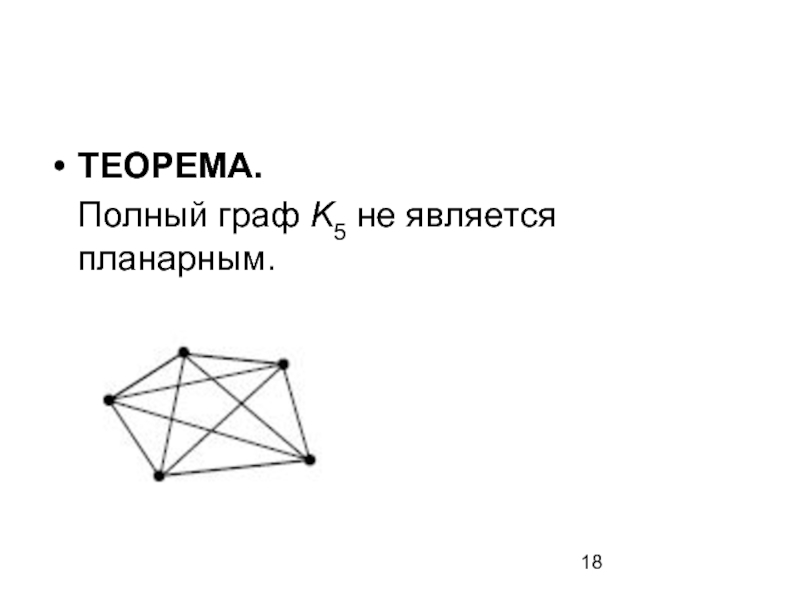
- 18. ТЕОРЕМА. Полный граф K5 не является планарным.
- 19. Доказательство: Граф К5 имеет пять вершин и
- 20. Признак планарности/непланарности графов
- 21. Необходимое и достаточное условие планарности графа
- 22. Теорема Понтрягина-Куратовского Граф планарен тогда
- 23. Понятие подграфа Граф G`(V`,E`) называется подграфом графа
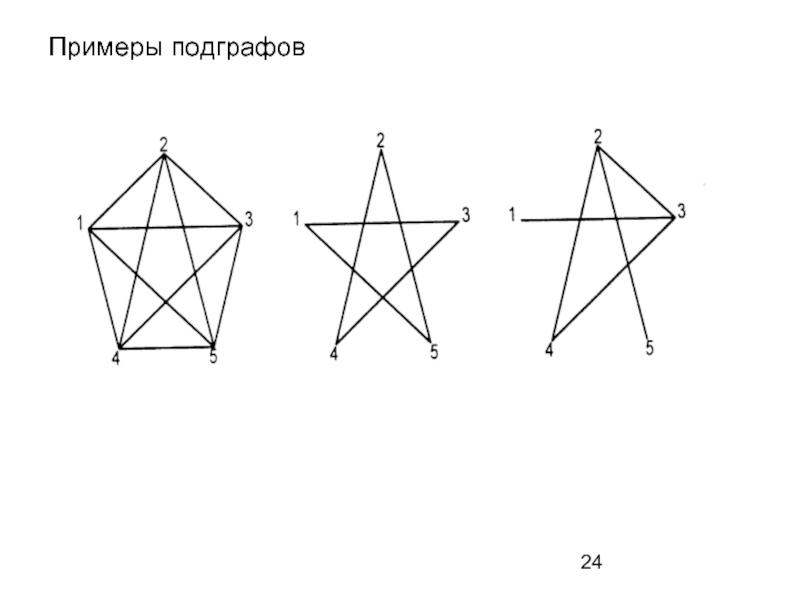
- 24. Примеры подграфов
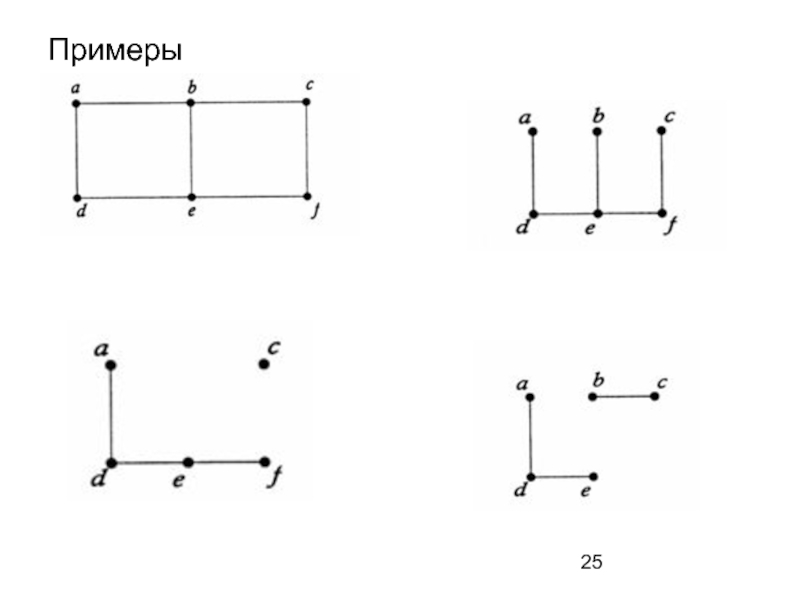
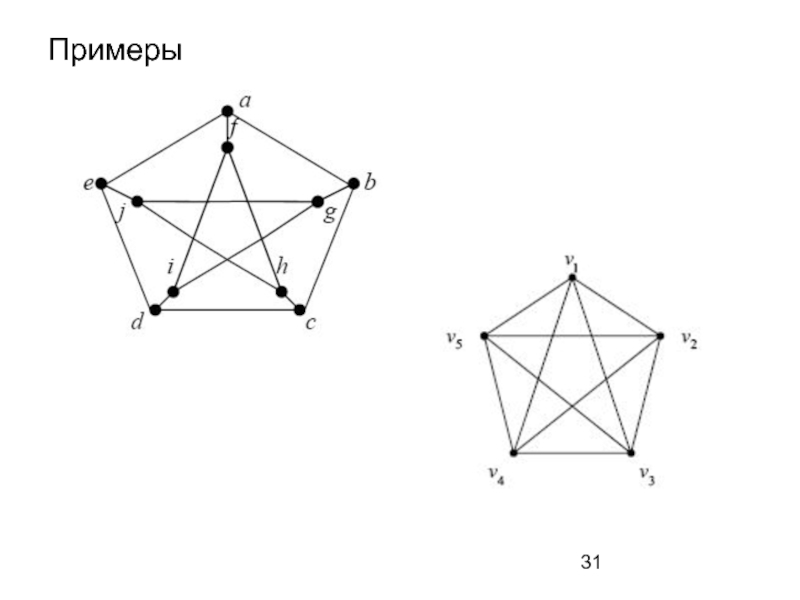
- 25. Примеры
- 26. Понятие гомеоморфности графов Два графа называются гомеоморфными
- 27. Операция введения вершины в ребро Добавлением
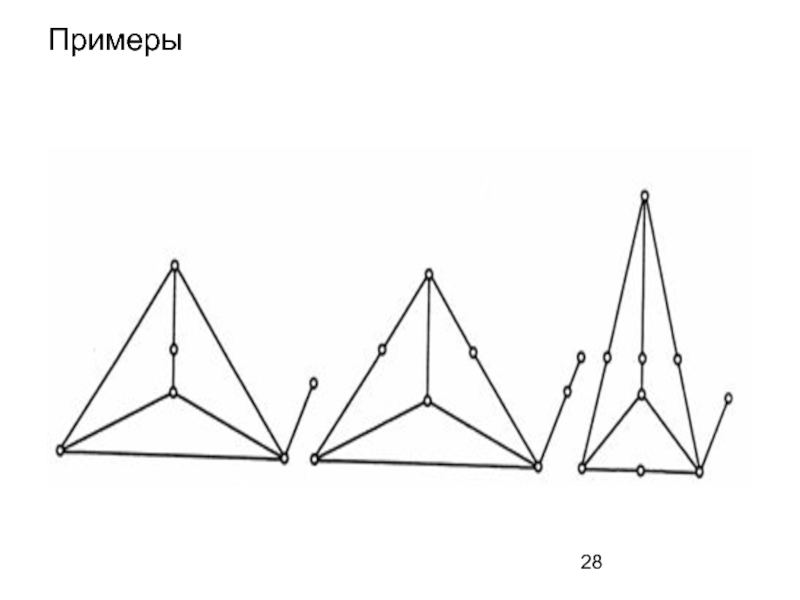
- 28. Примеры
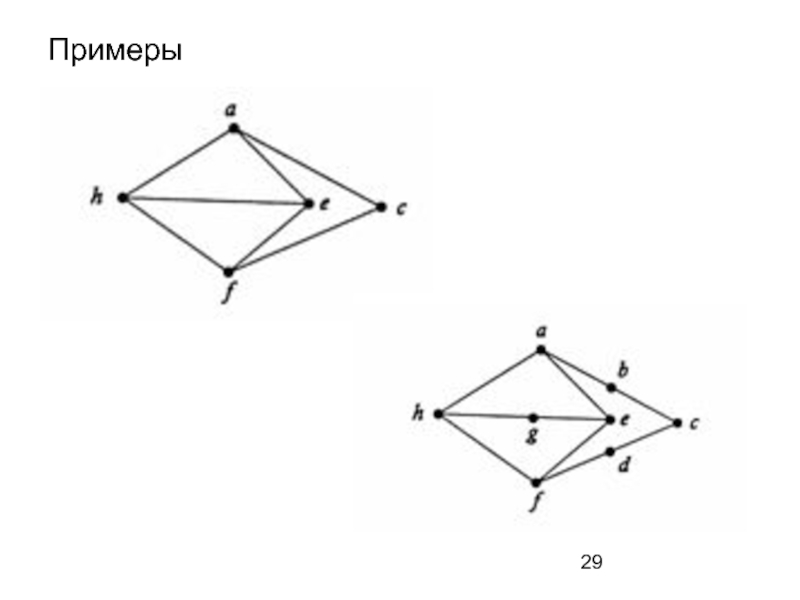
- 29. Примеры
- 30. Эквивалентная форма критерия планарности Теорема. Граф планарен
- 31. Примеры
- 32. Теорема. Если два связных графа
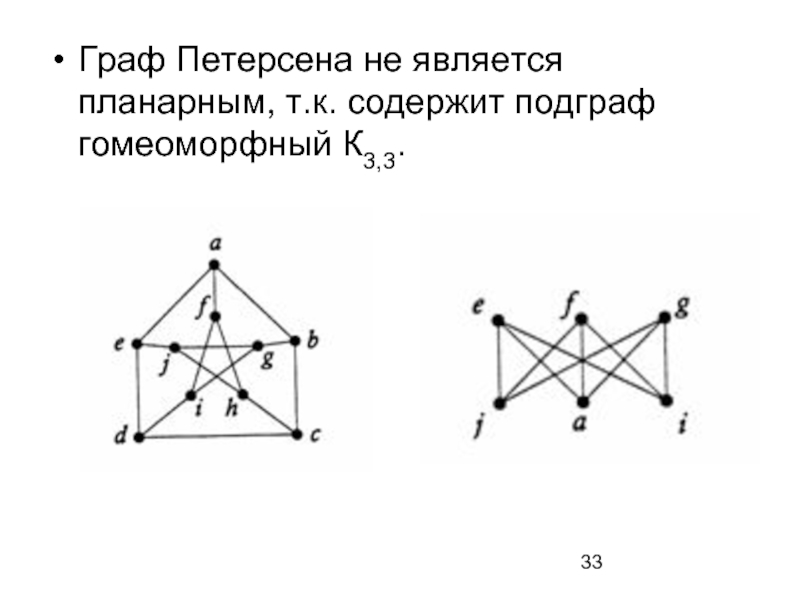
- 33. Граф Петерсена не является планарным, т.к. содержит подграф гомеоморфный К3,3.
- 34. Мера непланарности Для непланарных графов вводятся характеристики,
- 35. Мера непланарности Наименьшее число ребер, удаление которых
Слайд 2
При проектировании интегральных микросхем возникает задача построения графа с непересекающимися ребрами.
Слайд 3ОПРЕДЕЛЕНИЕ
Планарным графом называется граф,
который может быть изображен в
плоскости, так что его
ребра не
пересекаются.
Граф, который не является пла-
нарным, называется непланарным.
пересекаются.
Граф, который не является пла-
нарным, называется непланарным.
Слайд 7Понятие плоского графа
Плоским графом называется граф, вершины которого являются точками плоскости,
а ребра – непрерывными плоскими линиями без самопересечений, которые соединяют соответствующие вершины так, что никакие два ребра не имеют общих точек, кроме инцидентной им обоим вершиной.
Слайд 9 Если граф планарен и нарисован так,
что никакие линии не пересекаются, и
его
необходимо разрезать вдоль ребер, то
граф окажется разделенным на части,
включая внешнюю часть.
Такие части называются гранями.
необходимо разрезать вдоль ребер, то
граф окажется разделенным на части,
включая внешнюю часть.
Такие части называются гранями.
Слайд 10Грань планарного графа – максимальный участок плоскости такой, что любые две
точки этого участка могут быть соединены кривой, не пересекающей ребро графа.
Границей грани называется множество вершин и ребер, принадлежащих этой грани.
Граница каждой грани является циклом.
Границей грани называется множество вершин и ребер, принадлежащих этой грани.
Граница каждой грани является циклом.
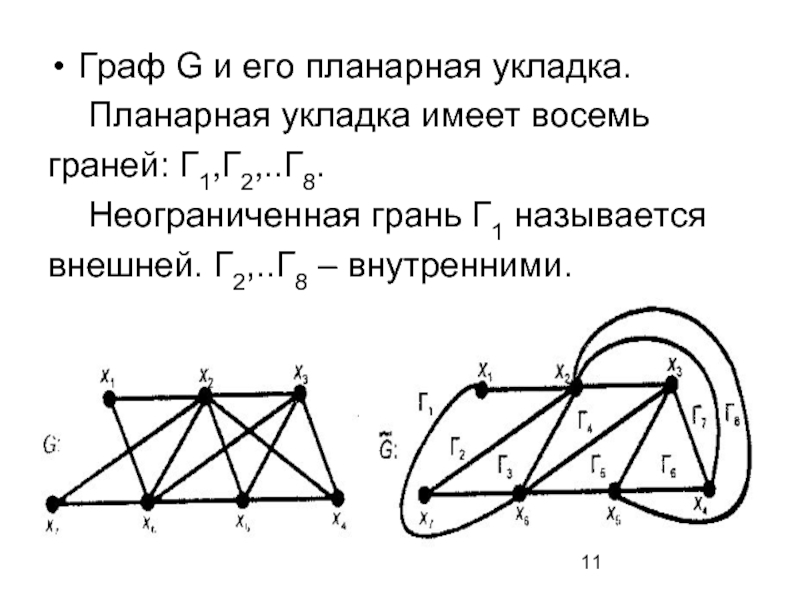
Слайд 11Граф G и его планарная укладка.
Планарная укладка имеет восемь
граней: Г1,Г2,..Г8.
Неограниченная грань
Г1 называется
внешней. Г2,..Г8 – внутренними.
внешней. Г2,..Г8 – внутренними.
Слайд 12
Всегда имеется одна неограниченная внешняя грань, все остальные грани называются внутренними.
Если
в плоском графе нет циклов, то у него имеется только одна грань.
Слайд 13В данной укладке планарного графа есть грани, границы которых являются простыми
циклами длины 5 и 3.
Слайд 15Теорема Эйлера
ТЕОРЕМА.
Если G – связный планарный граф, содержащий υ вершин,
e ребер и f граней, то υ – e + f = 2.
Слайд 17Лемма.
В произвольном связном планарном графе G с количеством вершин не
менее трех имеет место неравенство
3υ – e ≥ 6.
3υ – e ≥ 6.
Слайд 19Доказательство:
Граф К5 имеет пять вершин и десять ребер.
3υ – e =
3*5 – 10 = 5
Согласно Лемме: в произвольном
связном планарном графе G с
количеством вершин не менее трех имеет
место неравенство 3υ – e ≥ 6.
Следовательно граф К5 непланарный.
Согласно Лемме: в произвольном
связном планарном графе G с
количеством вершин не менее трех имеет
место неравенство 3υ – e ≥ 6.
Следовательно граф К5 непланарный.
Слайд 21
Необходимое и достаточное условие планарности графа сформулировано в теореме Понтрягина-Куратовского
Лев Семенович
Понтрягин (1908-1988)-советский математик
Казимеж Куратовский (1896-1980)-польский математик
Казимеж Куратовский (1896-1980)-польский математик
Слайд 22
Теорема Понтрягина-Куратовского
Граф планарен тогда и только тогда, когда он не содержит
подграфов, гомеоморфных К5 или К3,3.
Слайд 23Понятие подграфа
Граф G`(V`,E`) называется подграфом графа G(V,E), если V` V
и E` E.
Таким образом каждая вершина в G` является вершиной в G, и каждое в G` является ребром в G.
Таким образом каждая вершина в G` является вершиной в G, и каждое в G` является ребром в G.
Слайд 26Понятие гомеоморфности графов
Два графа называются гомеоморфными или тождественными с точность до
вершины степени 2, если они могут быть получены с одного и того же графа с помощью операции введения вершины в ребро степени 2.
Слайд 27Операция введения вершины в ребро
Добавлением вершины w в ребро (u,v) называется
операция, в результате которой получаем два ребра (u,w) и (w,v), а ребро (u,v) удаляется из графа G.
Слайд 30Эквивалентная форма критерия планарности
Теорема.
Граф планарен тогда и только тогда,
когда в нем
нет подграфов,
стягиваемых к графам К5 или К3,3.
стягиваемых к графам К5 или К3,3.
Слайд 32
Теорема.
Если два связных графа гомеоморфны,
то они либо оба планарны,
либо оба
непланарны.
Теорема.
Произвольный граф, гомеоморфный графу К3,3 или К5,не является планарным.
непланарны.
Теорема.
Произвольный граф, гомеоморфный графу К3,3 или К5,не является планарным.
Слайд 34Мера непланарности
Для непланарных графов вводятся характеристики, представляющие ту или иную меру
непланарности.
Если граф непланарен, то для его геометрической реализации удаляются отдельные ребра(их переносят на другую плоскость).
Если граф непланарен, то для его геометрической реализации удаляются отдельные ребра(их переносят на другую плоскость).
Слайд 35Мера непланарности
Наименьшее число ребер, удаление которых приводит к планарному графу, называется
числом планарности или искаженностью sk(G) графа G.
Для числа планарности полного графа справедлива следующая формула:
sk (G) = Cn2 – 3n +6, n≥3.
Для числа планарности полного графа справедлива следующая формула:
sk (G) = Cn2 – 3n +6, n≥3.