- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория автоматов презентация
Содержание
- 1. Теория автоматов
- 2. Предмет теории автоматов Теория автоматов ─ раздел
- 3. В ТА математические модели создаются с
- 4. Схема операционного устройства (ОУ) УА – управляющий
- 5. Абстрактные цифровые автоматы (АЦА) АЦА - это
- 6. Цифровой автомат – математическая модель
- 7. Z: z1 - любой символ,
- 8. Задача: УУ осуществляет сканирование входного текста посимвольно
- 9. Классы абстрактных автоматов (АА) Классификация АА
- 10. По количеству различных состояний, в которых будет
- 11. По устойчивости состояний: асинхронный автомат - все
- 12. Автомат Мили (Mealy) Выходной сигнал зависит и
- 13. Модель С-автомата Имеет 2 выходных канала: по
- 14. Языки задания АА
- 15. Табличный способ задания Таблица выходов Таблица
- 16. Отмеченная таблица переходов автомата Мура δ:
- 17. Графический способ задания функций переходов и выходов
- 18. Пример: Отец, в зависимости от того, какие
- 19. Табличный способ задания δ: λ: Совмещенная таблица
- 20. Матричный способ задания Матрица связей для автомата
- 21. Преобразование автомата Мура в автомат Мили S1
- 22. Преобразование автомата Мура в автомат Мили Из
- 23. Преобразование автомата Мили в автомат Мура Каждому
- 24. Преобразование автомата Мили в автомат Мура z1/wi
- 25. Эквивалентность автоматов Автоматы с одинаковыми наборами входных
- 26. Задача минимизации АА Задача нахождения автомата с
- 27. Структурные цифровые автоматы (СЦА) СЦА описывает реальное
- 28. y - выходные сигналы первого рода
- 29. Установление соответствия абстрактных и структурных сигналов Установление
- 30. Пример установления соответствия между сигналами Определение количества
- 31. Методы структурного синтеза ЦА Основой всех методов
- 32. Канонический метод структурного синтеза Основой метода является
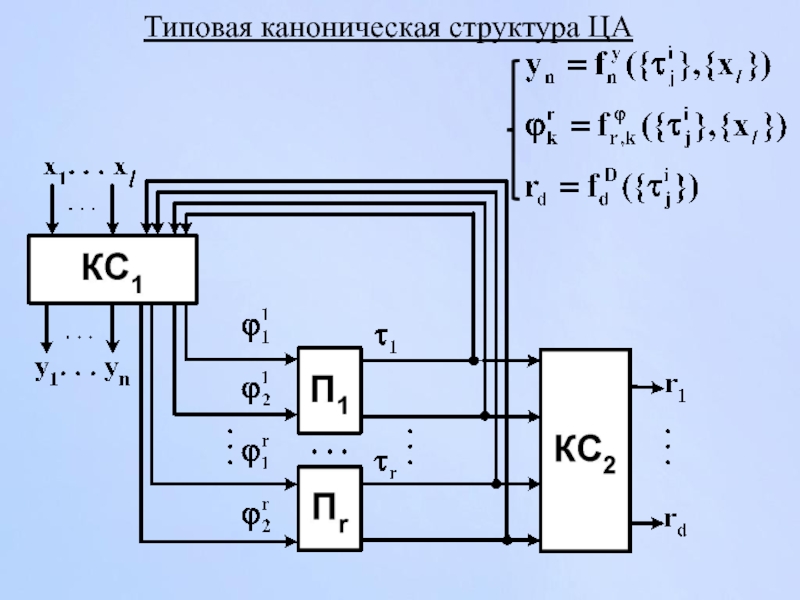
- 33. Типовая каноническая структура ЦА
- 34. Синтез автомата на триггерах Триггер - физический
- 35. Виды стандартных триггеров По логике работы и
- 36. D-триггер D-триггер - повторяет входной сигнал: через
- 37. T-триггер - меняет свое состояние на противоположное
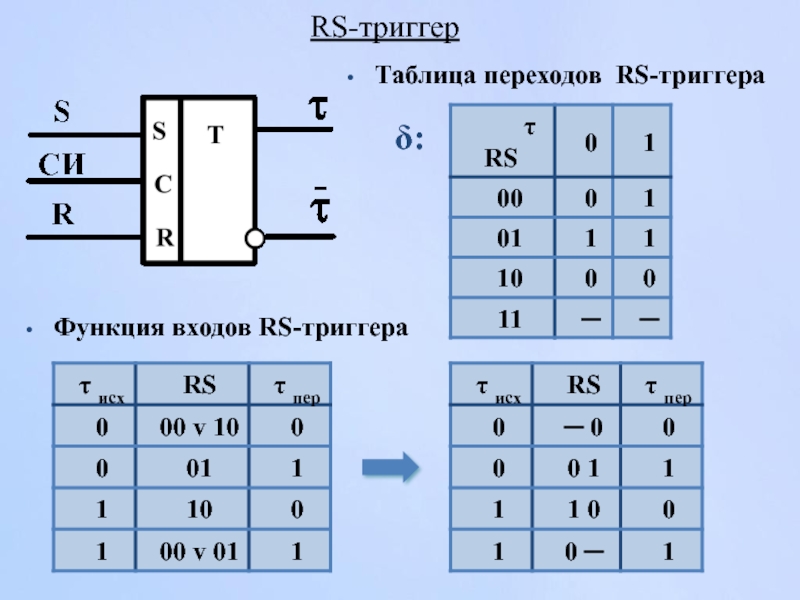
- 38. δ: Таблица переходов RS-триггера Функция входов RS-триггера RS-триггер
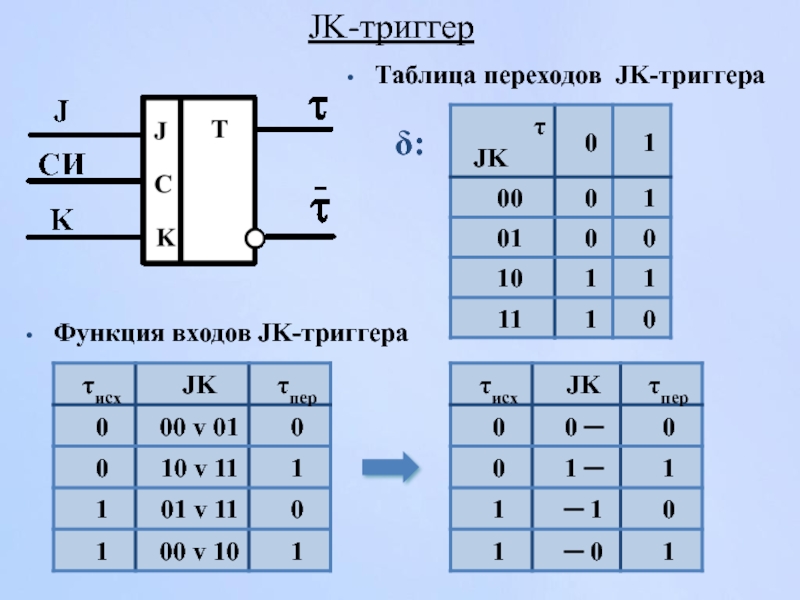
- 39. δ: Таблица переходов JK-триггера Функция входов JK-триггера JK-триггер
- 40. Минимизация комбинационной части автомата Цель минимизации уменьшение
- 41. Классическая минимизация СДНФ(СКНФ) => МДНФ(МКНФ) Нормальная форма
- 42. Получение абсолютных минимальных форм (АМФ) АМФ -
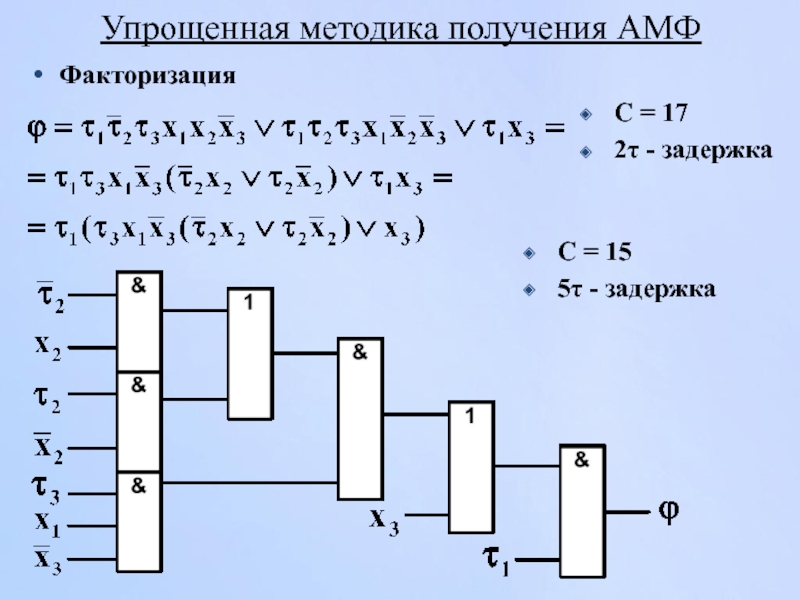
- 43. Упрощенная методика получения АМФ Факторизация С =
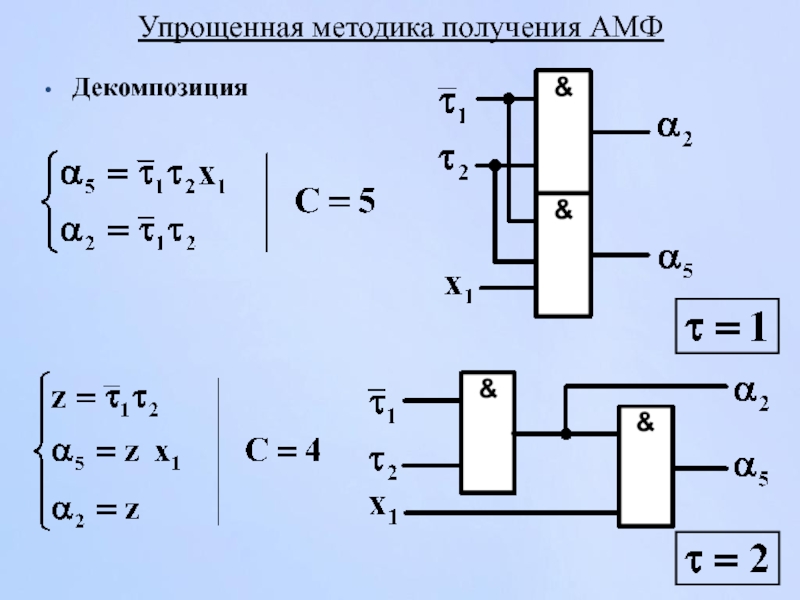
- 44. Упрощенная методика получения АМФ Декомпозиция
- 45. Кодирование сигналов и состояний Сложность комбинационной
- 46. y1y2 4 3 Произвольное кодирование y1y2 2
- 47. Задача: построить СЦА на основе заданной таблицы
- 48. Кодирование Кодирование выходных сигналов I рода по
- 49. τ1τ2 x1x2 00
- 50. Получение функций возбуждения, используя таблицу переходов и
- 51. τ1τ2 x1x2
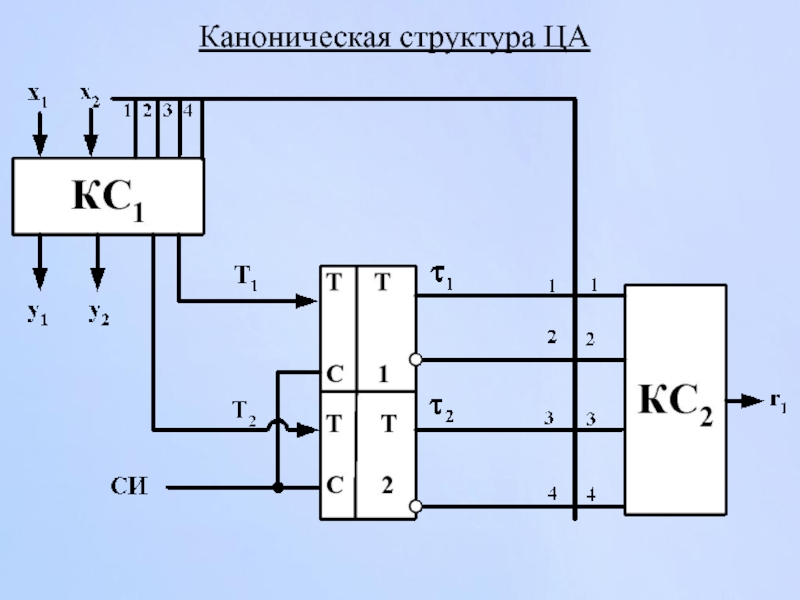
- 52. Каноническая структура ЦА
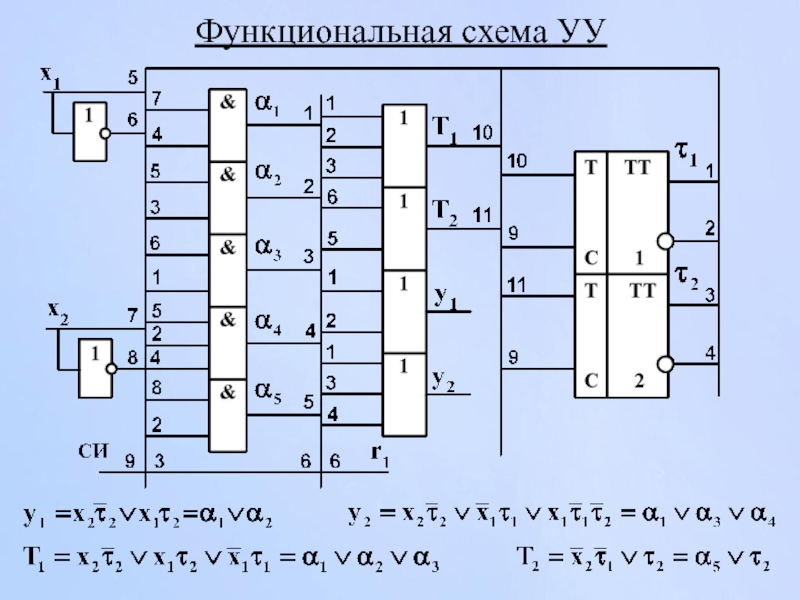
- 53. Функциональная схема УУ
- 54. Работа автомата и обеспечение устойчивости функционирования
- 55. Двоичные сигналы и уровни их представления Сигнал
- 56. При работе со структурными сигналами используется их
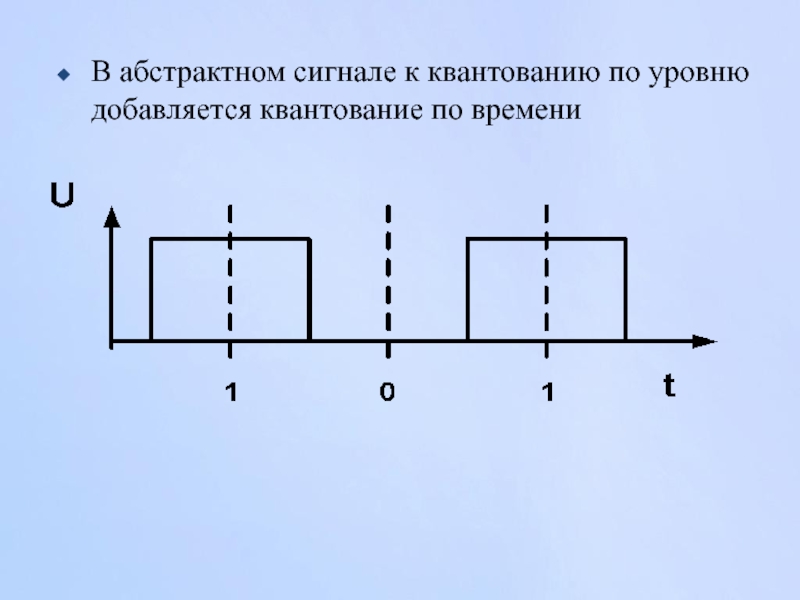
- 57. В абстрактном сигнале к квантованию по уровню добавляется квантование по времени
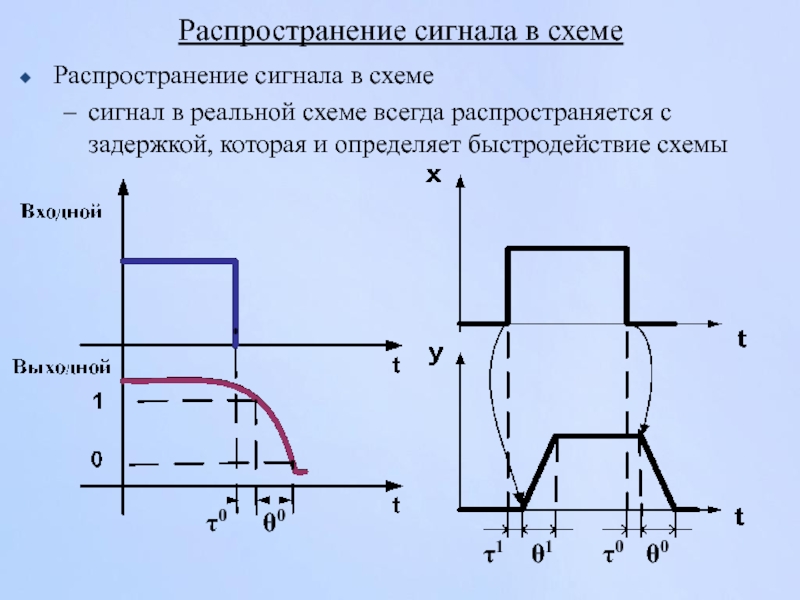
- 58. Распространение сигнала в схеме сигнал в реальной
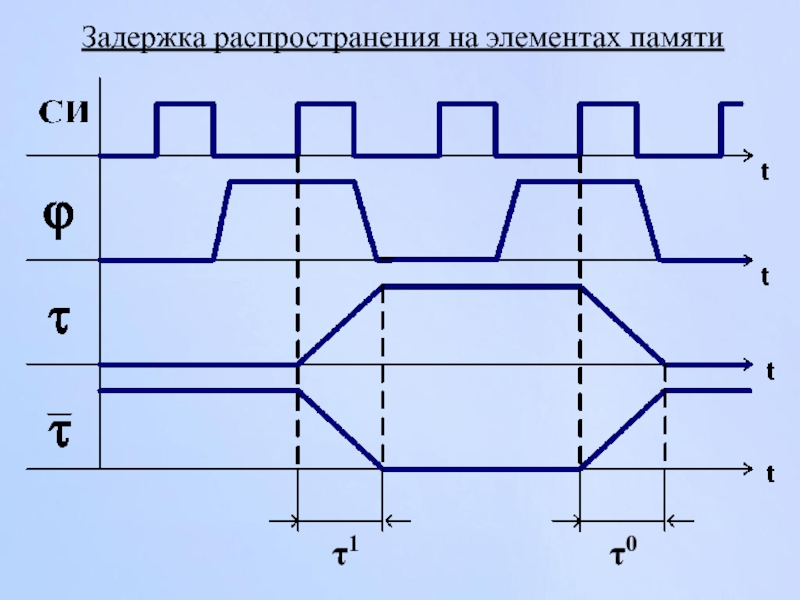
- 59. Задержка распространения на элементах памяти τ1 τ0
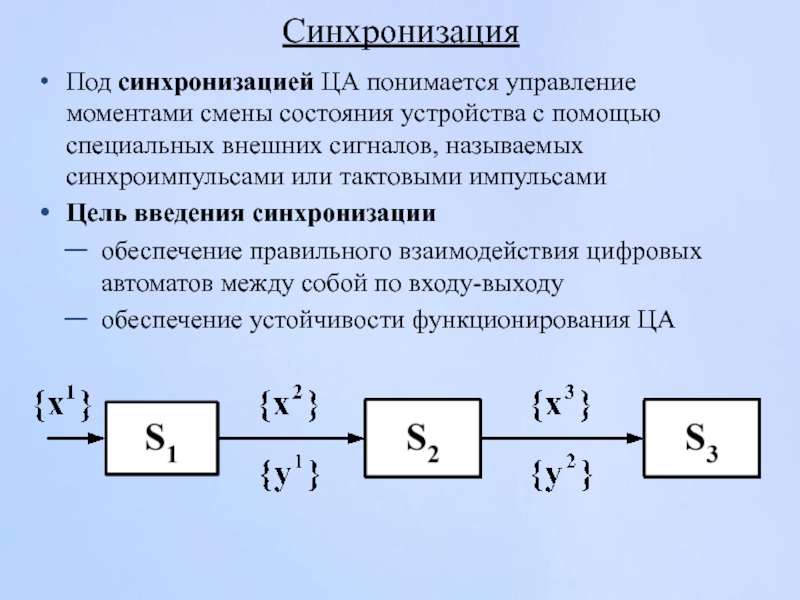
- 60. Синхронизация Под синхронизацией ЦА понимается управление моментами
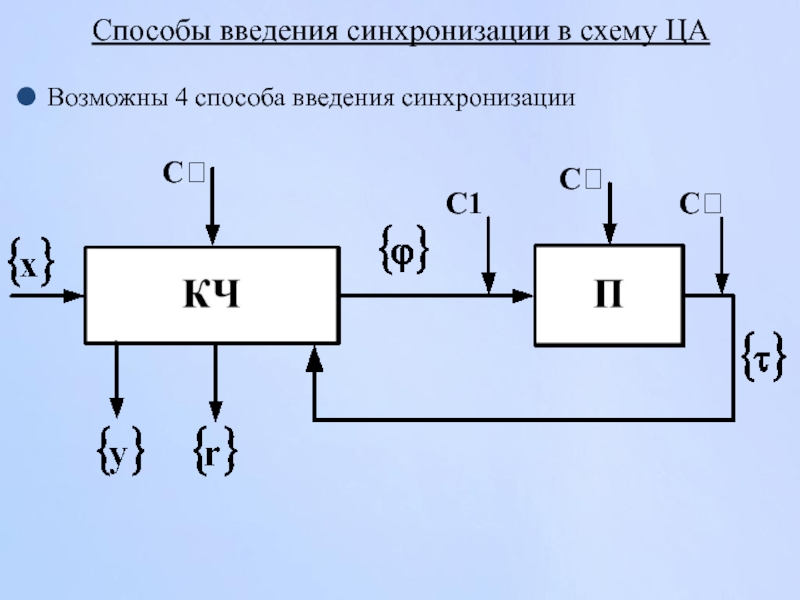
- 61. Способы введения синхронизации в схему ЦА Возможны 4 способа введения синхронизации С1 С С С
- 62. Достоинство отсутствует необходимость усложнять КЧ автомата Недостаток
- 63. Достоинство позволяет реализовать многофазную синхронизацию Недостаток существенное
- 64. Факторы неустойчивой работы ЦА Неодновременное поступление
- 65. Синхронные и асинхронные ЦА Условно-устойчивые состояния
- 66. Временная диаграмма работы автомата с неустойчивым состоянием
- 67. Работа асинхронного автомата без введения синхронизации Рассматриваем
- 68. Временная диаграмма ТА - такт автомата τφ
- 69. Согласование автоматов по входу-выходу x1 : 0
- 70. Диаграмма перехода в другое состояние при неодновременной подаче входных сигналов
- 71. Причины нарушения Наличие разброса моментов переключения
- 72. Методы обеспечения устойчивости состояний Ограничить длительность синхроимпульса
- 73. I. Импульсная синхронизация Недостатки импульсной синхронизации 1.
- 74. II. Многофазная синхронизация Синхроимпульсы вводятся в схему непосредственно на конъюнкторы, обеспечивающие формирование сигналов возбуждения памяти.
- 75. Возможность использования многоступенчатой синхронизации зависит от графа
- 76. III. Использование двухступенчатых элементов памяти Недостаток :
- 77. III. Использование двухступенчатых элементов памяти Принцип действия
- 78. Временная диаграмма введения синхронизации элементов памяти Тси
- 79. IV. Использование триггеров с динамическим управлением по
- 80. Гонки в автомате Гонки могут возникать только
- 81. В частичных автоматах, где используются не все
- 82. Способы устранения гонок Аппаратные импульсная синхронизация
- 83. Соседнее кодирование Условия возможности соседнего кодирования отсутствие
- 84. Пример соседнего кодирования На всех переходах должен
- 85. Кодирование с учетом условий развязки пар переходов
- 86. Операционные устройства ОУ предназначено для выполнения набора
- 87. Концепция операционного и управляющего автоматов Y={ym} –
- 88. Концепция операционного и управляющего автоматов ОА предназначен
- 89. Операционный элемент (ОЭ) Операционный элемент - устройство,
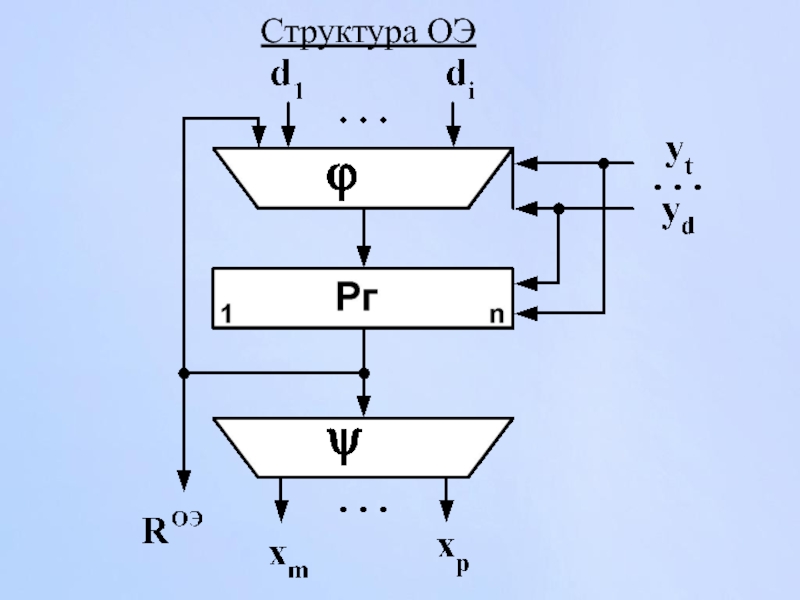
- 90. Структура ОЭ
- 91. Типовые микрооперации, выполняемые ОЭ с памятью Прием
- 92. Сдвиги y1: A := L1(A).0 y2: A
- 93. Инверсия - изменение значения разряда слова на
- 94. Формирование логических условий x1: A{1} x2: A=0
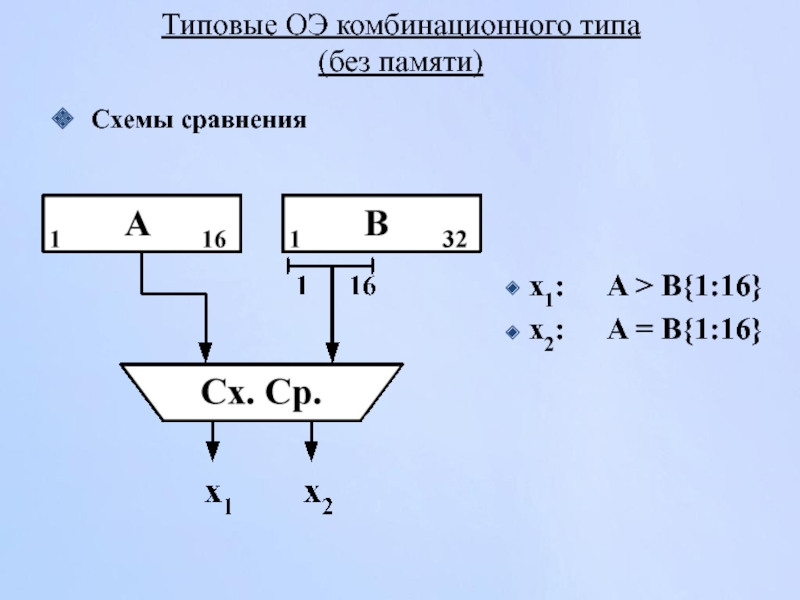
- 95. Типовые ОЭ комбинационного типа (без памяти)
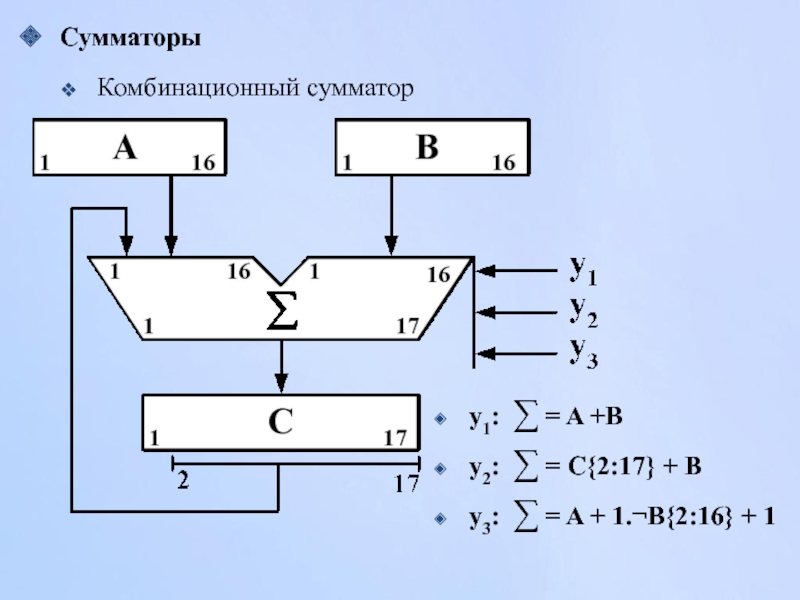
- 96. Сумматоры y1: ∑ = A +B y2:
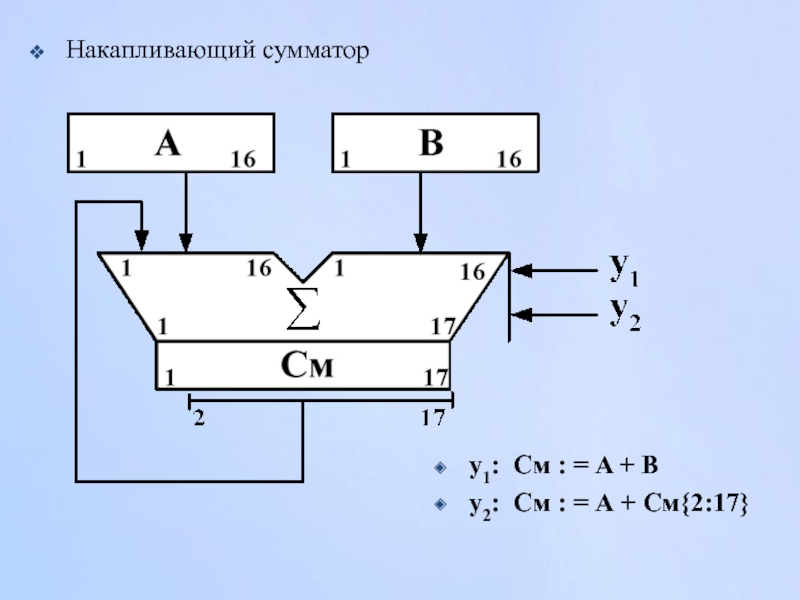
- 97. y1: См : = A + B
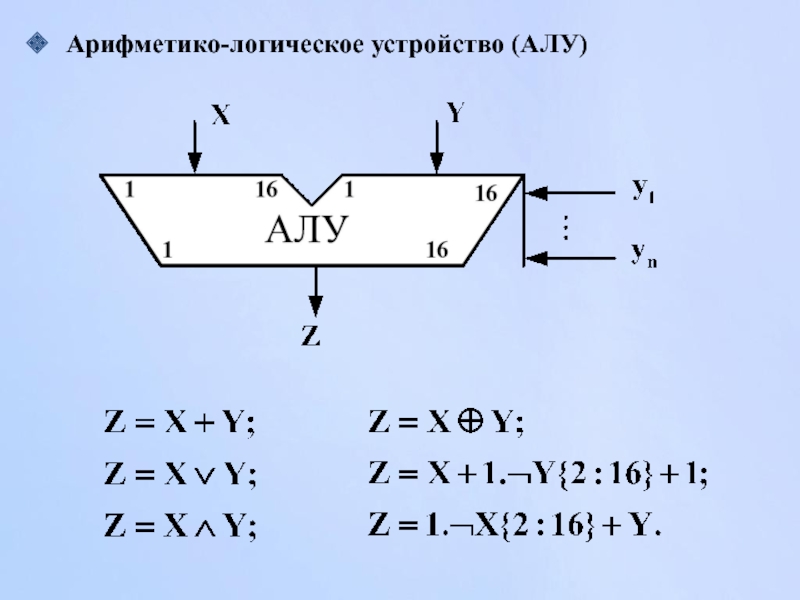
- 98. Арифметико-логическое устройство (АЛУ)
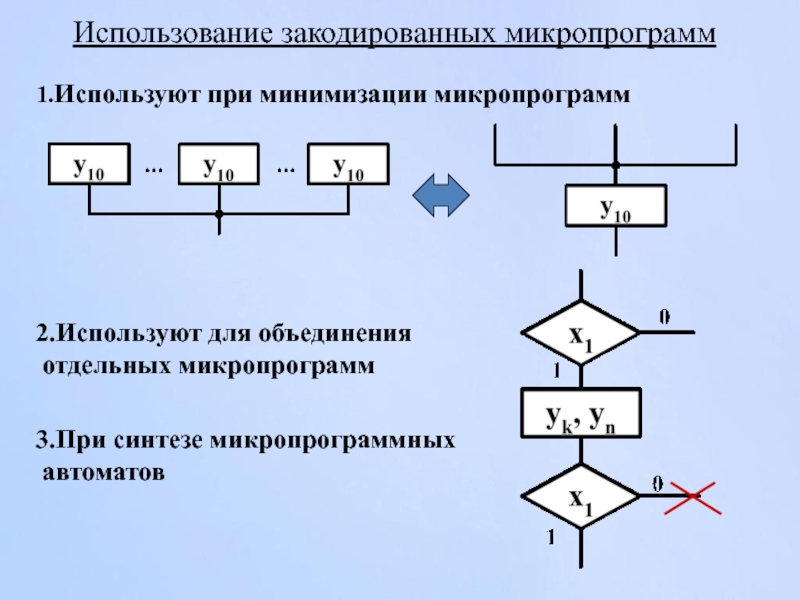
- 99. Использование закодированных микропрограмм Используют при минимизации микропрограмм
- 100. Совместимость микроопераций Совместимость микроопераций - свойство микроопераций, гарантирующее их параллельное совместное выполнение Алгоритмическая Структурная
- 101. Объединение и минимизация микропрограмм Цель получение минимальной
- 102. 2. Получение объединенной микропрограммы
- 103. 3. Минимизация объединенной микропрограммы возможна, если для
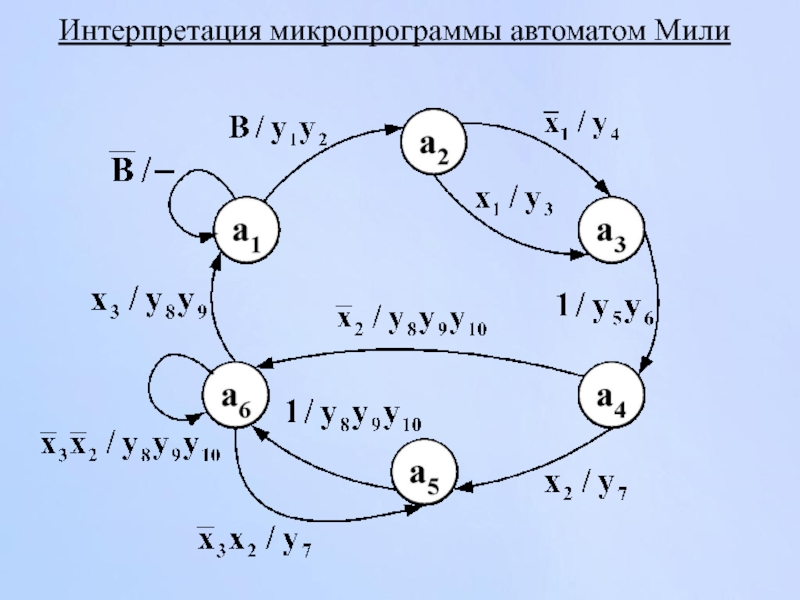
- 104. Интерпретация микропрограммы автоматом Мили Отметка закодированного графа
- 105. Содержательный граф микропрограммы
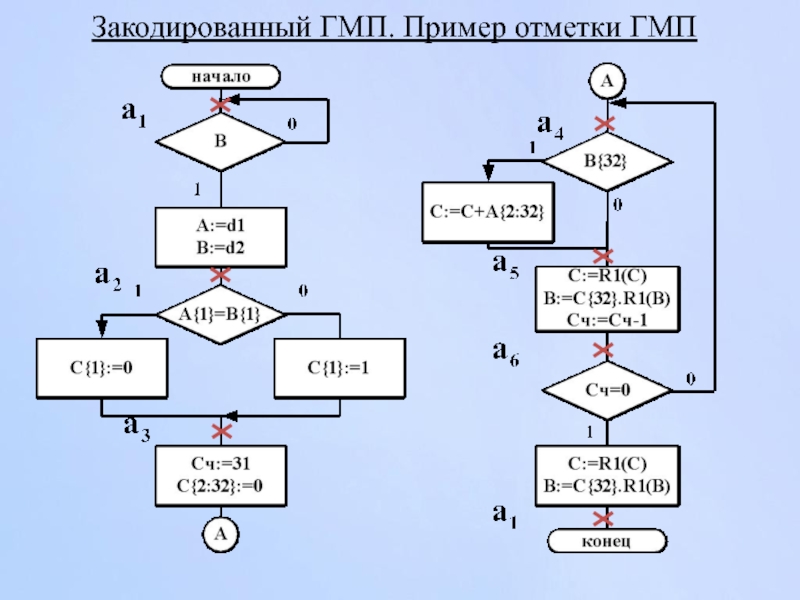
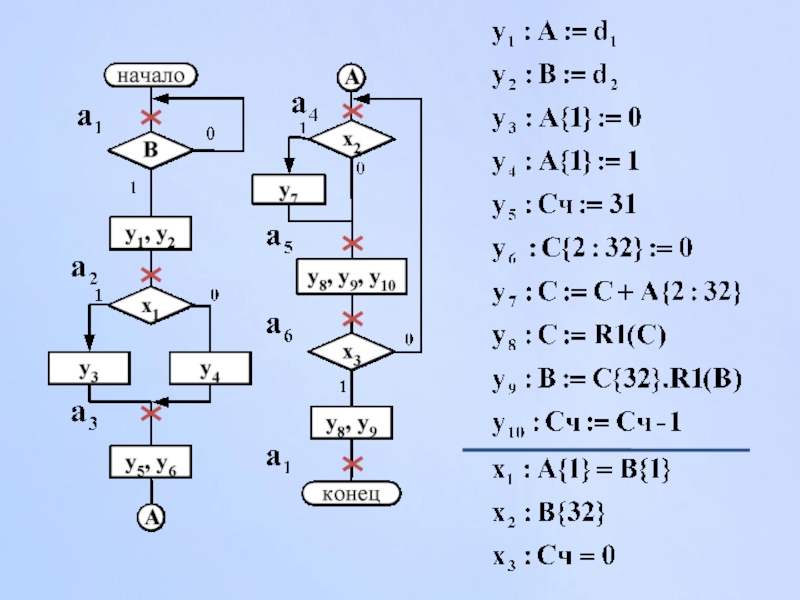
- 106. Закодированный ГМП. Пример отметки ГМП
- 108. Пути перехода в ГМП Путь перехода в
- 109. Пути перехода в ГМП. Исключения Путь перехода
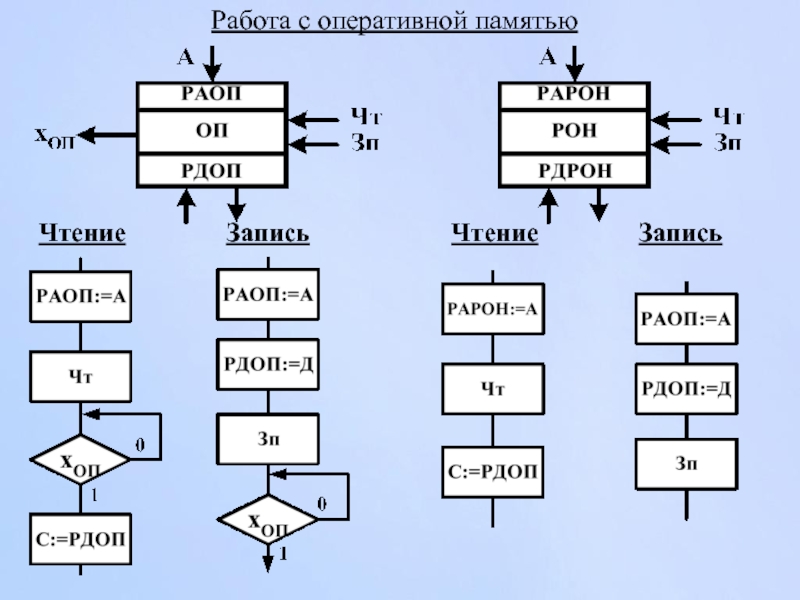
- 110. Работа с оперативной памятью Чтение Запись Чтение Запись
- 111. Интерпретация микропрограммы автоматом Мили
- 112. Корректность интерпретации микропрограммы автоматом Мили Корректная интерпретация
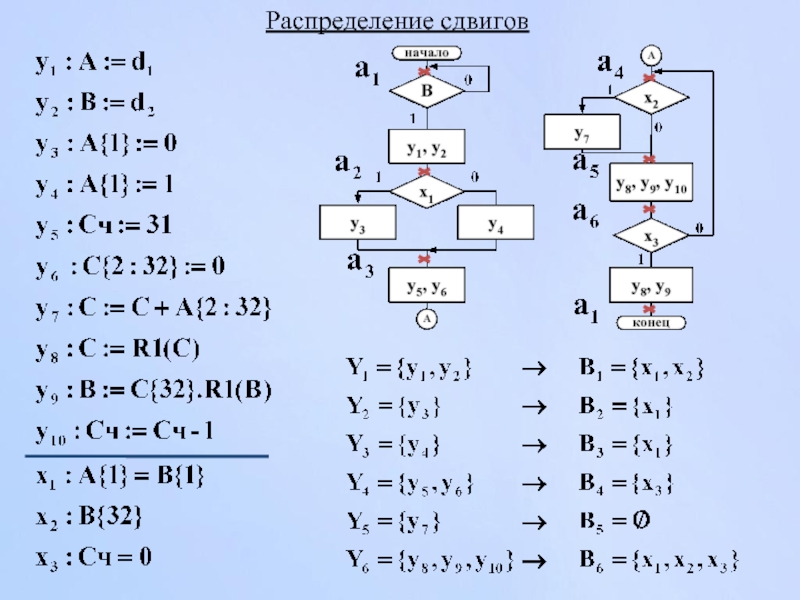
- 113. Распределение сдвигов
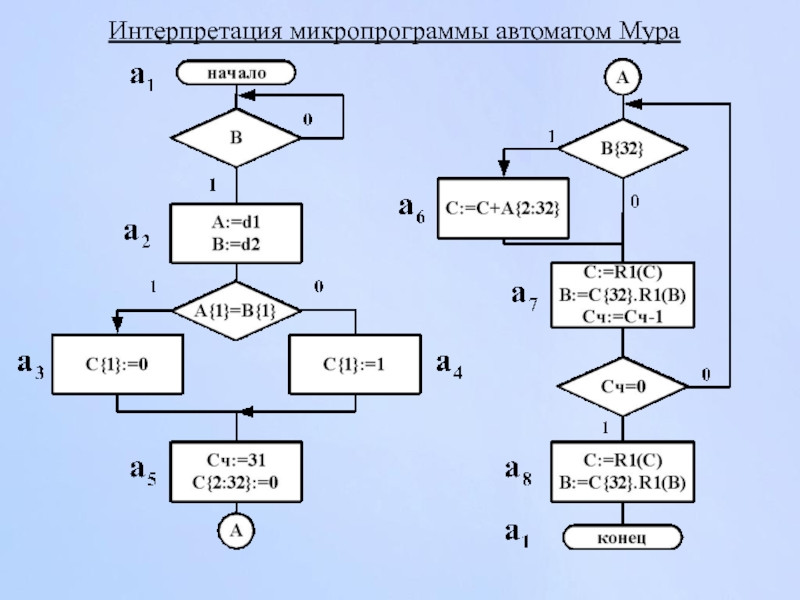
- 114. Интерпретация микропрограммы автоматом Мура
- 115. Пути перехода в ГМП. Исключения Путь перехода
- 116. Пути перехода в ГМП. Исключения Путь перехода
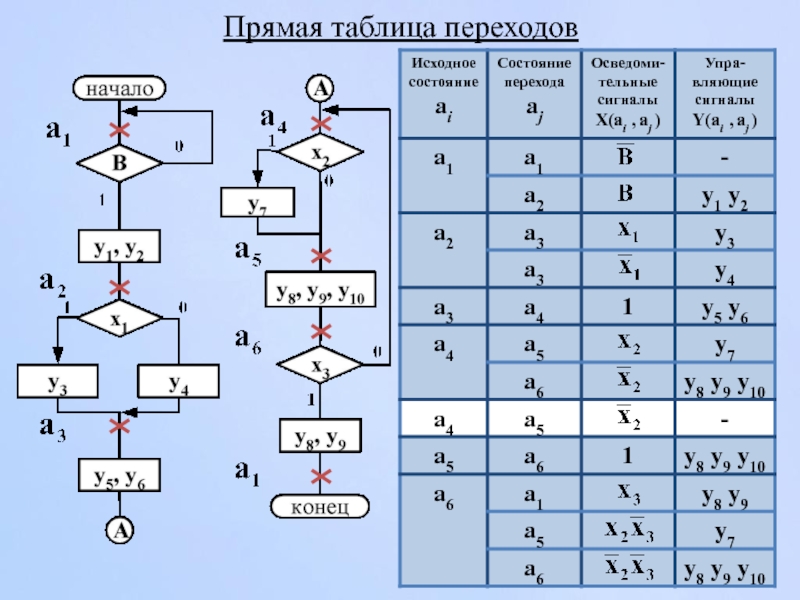
- 117. Прямая таблица переходов
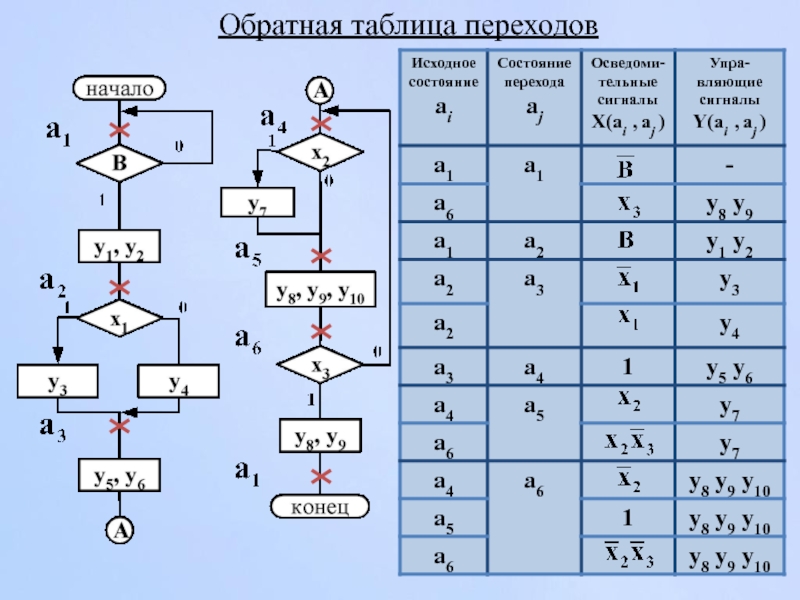
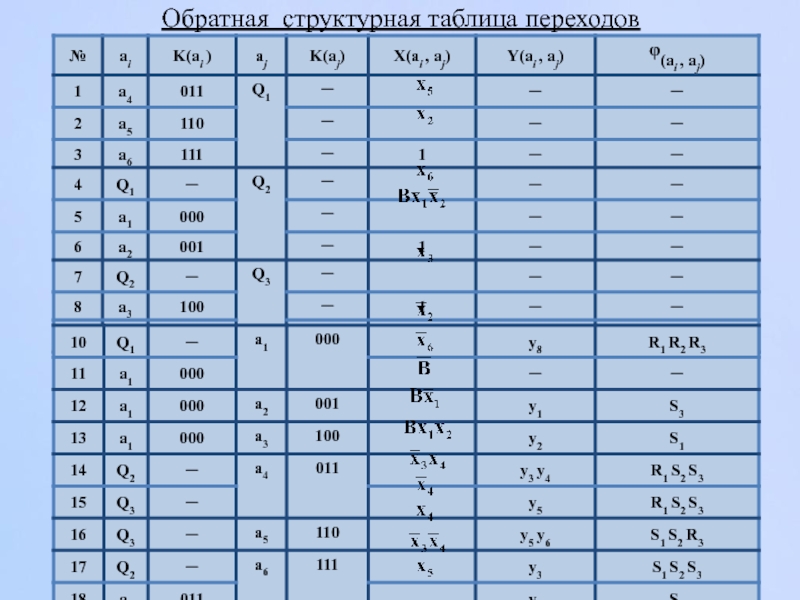
- 118. Обратная таблица переходов
- 119. Структурная организация ЦА с жесткой логикой Структура
- 120. Синтез УА с жесткой логикой Исходными данными
- 121. Интерпретационный метод синтеза Метод синтеза, основанный на
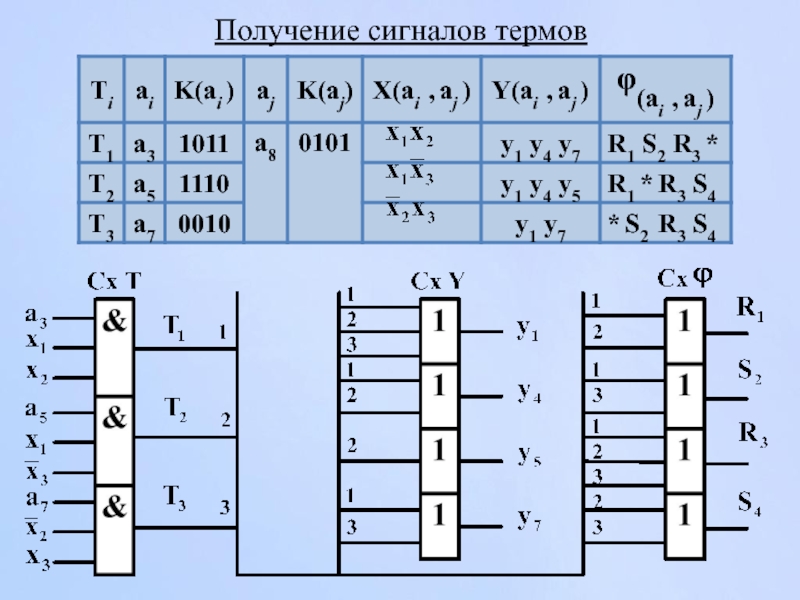
- 122. Получение сигналов термов
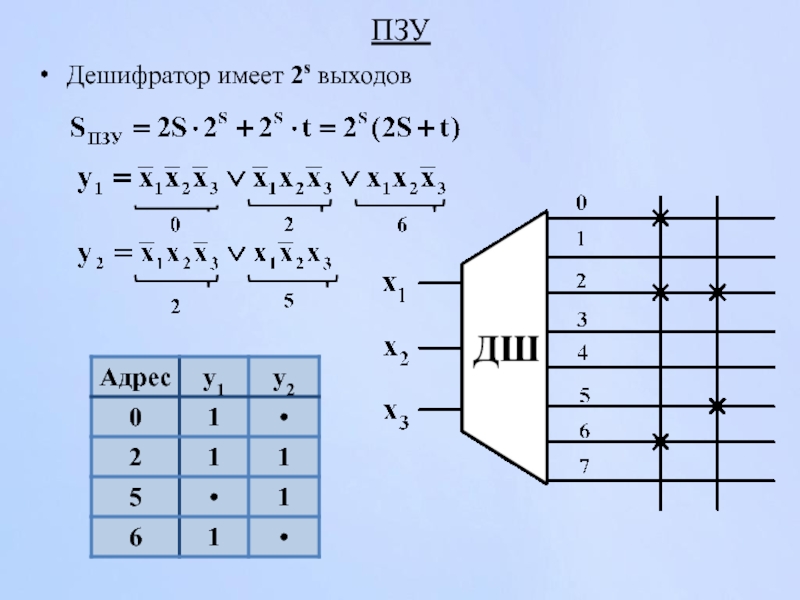
- 123. Дешифратор ДШ - КС, преобразующая позиционный двоичный
- 124. Схема дешифратора
- 125. τ2τ3 τ1 00
- 126. Построение двухступенчатого ДШ Преддешифратор состояний Выходная ступень дешифратора состояний
- 127. Предварительное объединение сигналов термов Предварительное объединение -
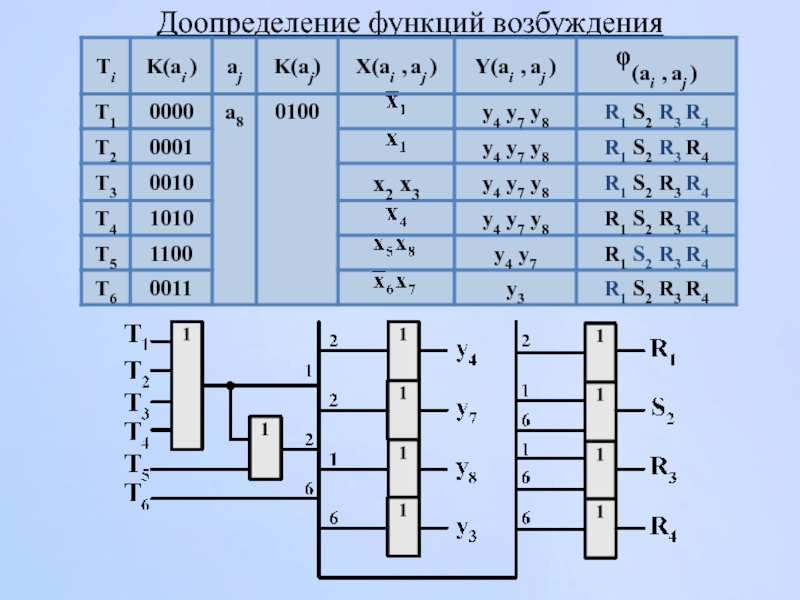
- 128. Доопределение функций возбуждения
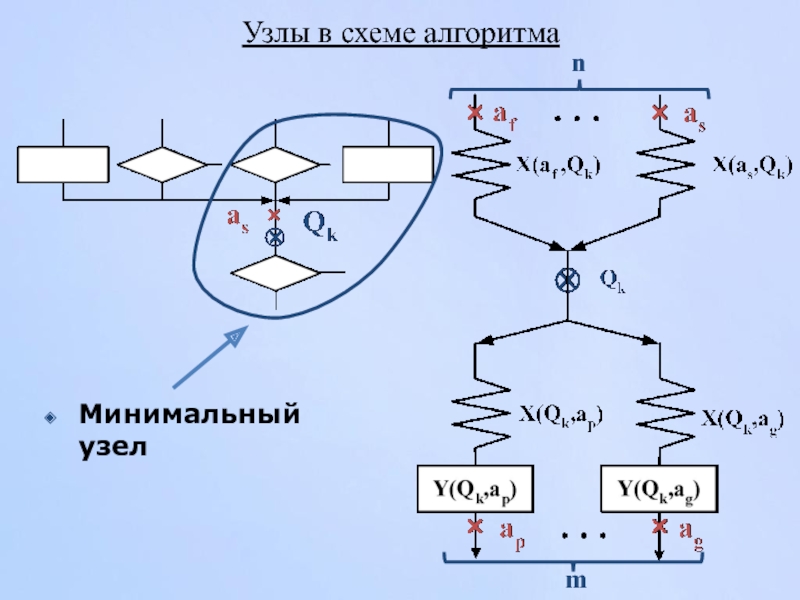
- 129. Узлы в схеме алгоритма Минимальный узел m n
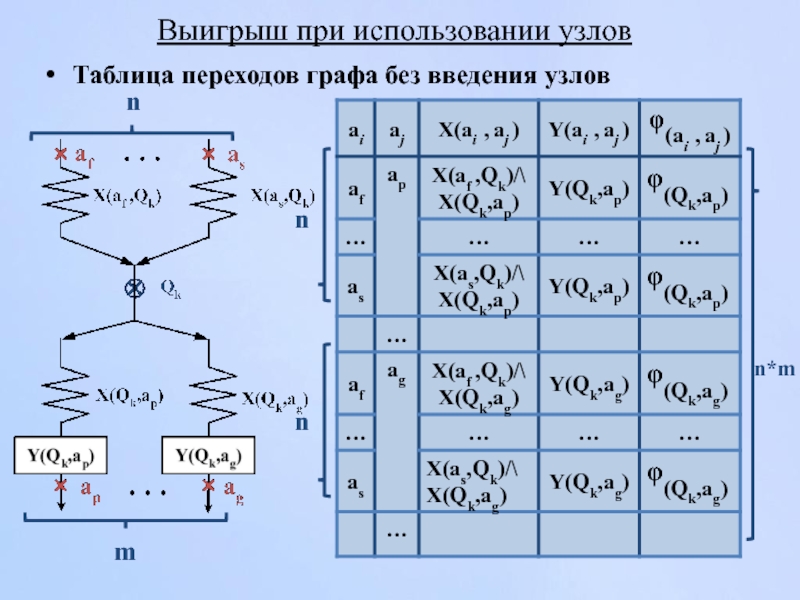
- 130. Выигрыш при использовании узлов Таблица переходов
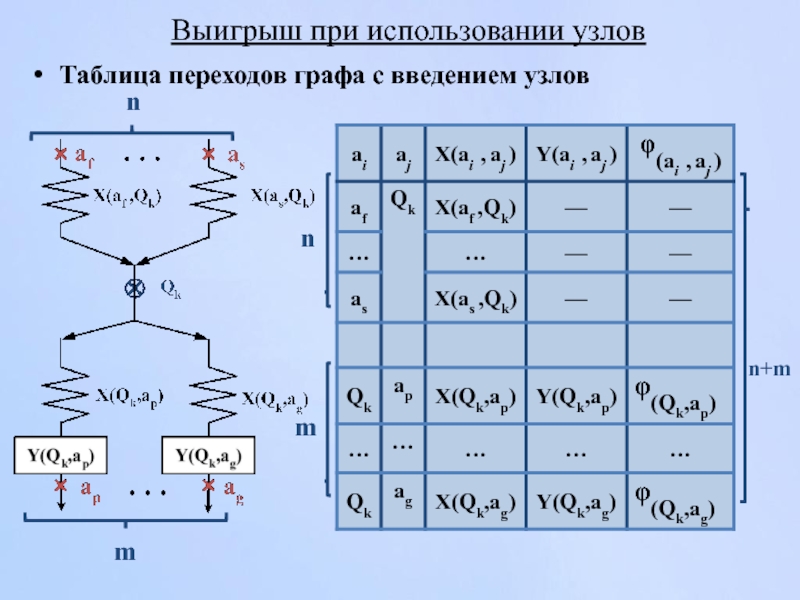
- 131. Таблица переходов графа с введением узлов Выигрыш
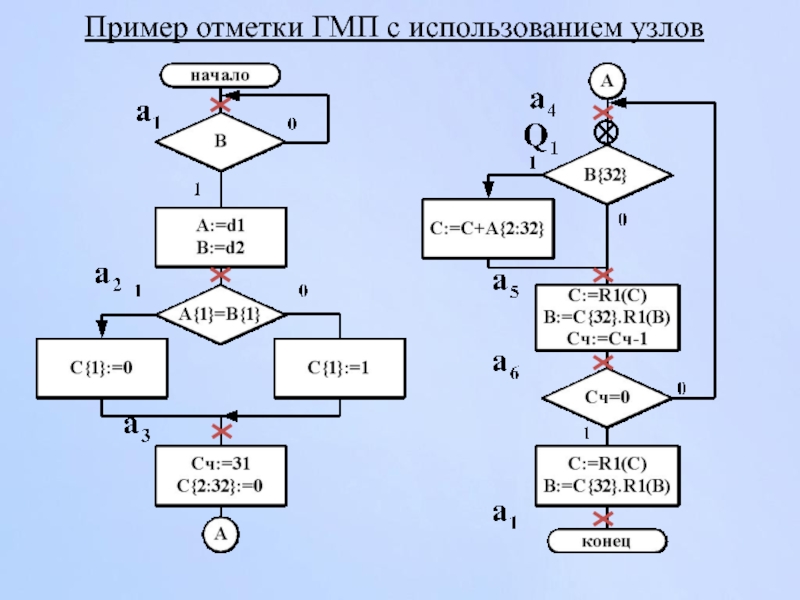
- 132. Пример отметки ГМП с использованием узлов
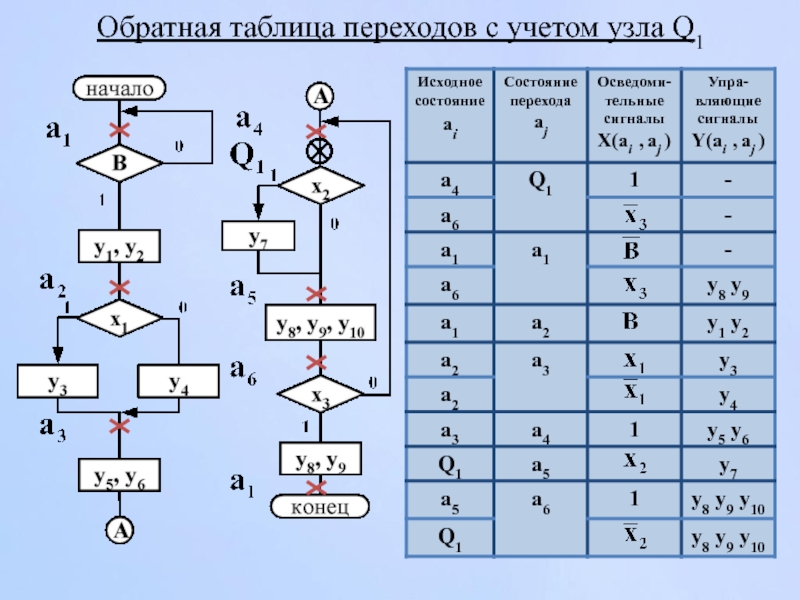
- 133. Обратная таблица переходов с учетом узла Q1
- 134. Учет узлов при построении комбинационной части автомата
- 135. Функции возбуждения на переходах из узлов Функции
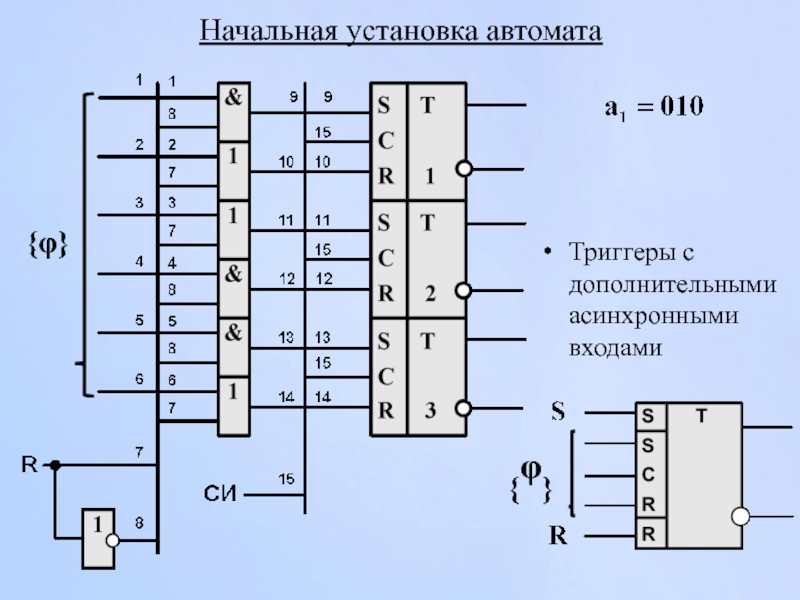
- 136. Начальная установка автомата Триггеры с дополнительными асинхронными входами {φ} {φ}
- 137. Запуск автомата Реализация запуска автомата : на
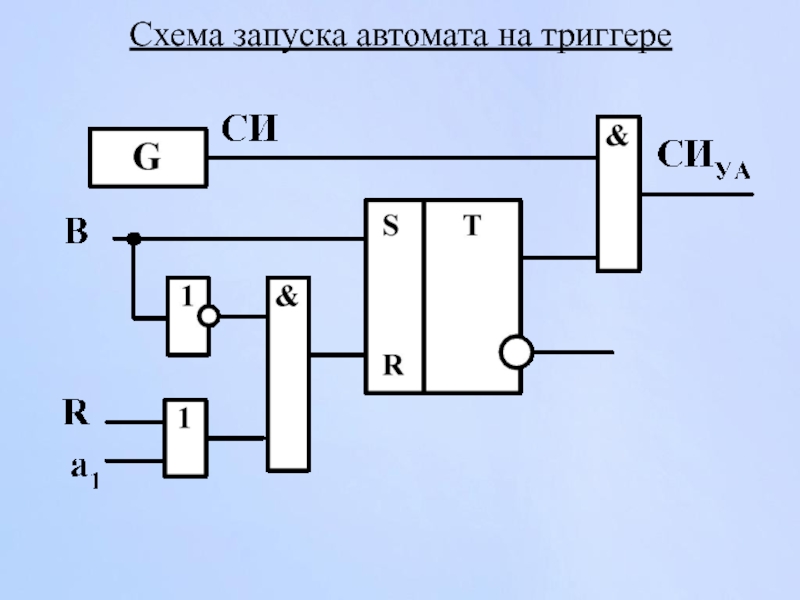
- 138. Схема запуска автомата на триггере
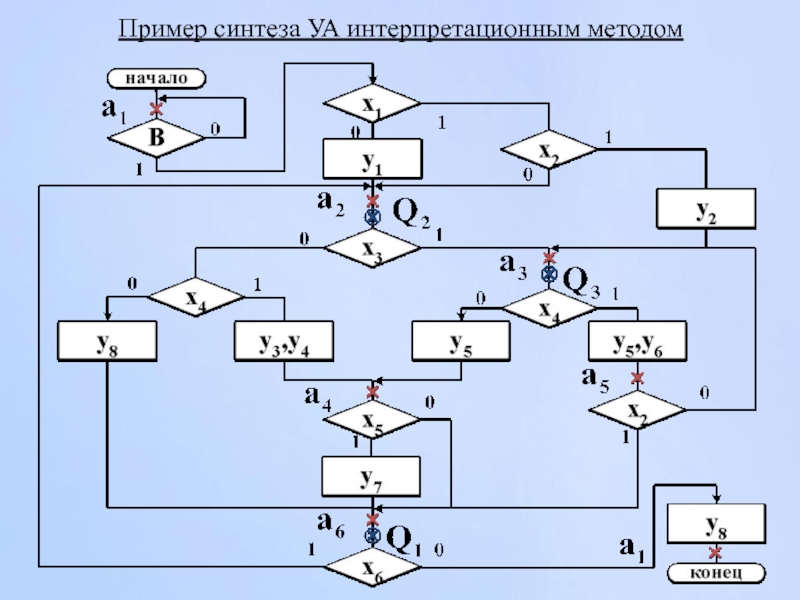
- 139. Пример синтеза УА интерпретационным методом
- 140. Обратная структурная таблица переходов
- 141. Системы канонических уравнений Кодирование состояний
- 142. Системы канонических уравнений
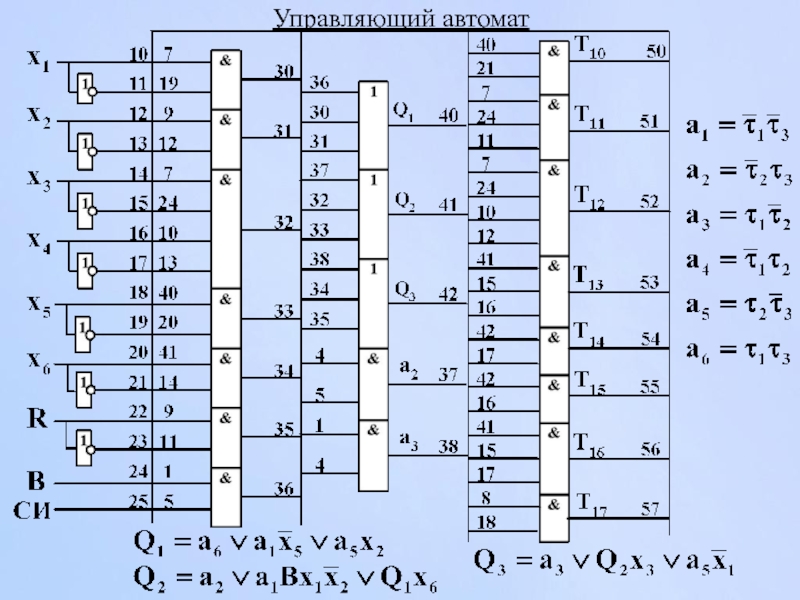
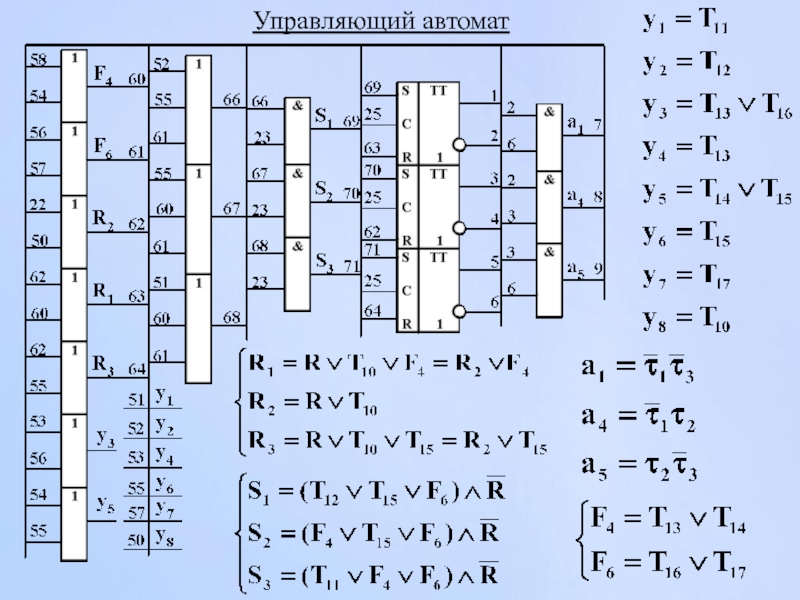
- 143. Управляющий автомат
- 144. Управляющий автомат
- 145. Синтез УА на программируемых логических устройствах
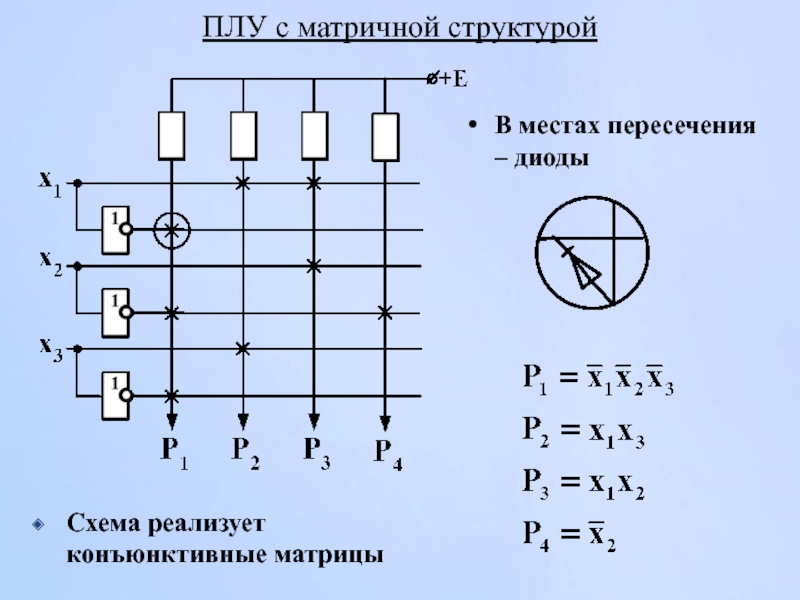
- 146. ПЛУ с матричной структурой В местах пересечения – диоды Схема реализует конъюнктивные матрицы
- 147. Схема реализует дизъюнктивные матрицы ПЛУ с матричной структурой В местах пересечения – транзисторы
- 148. ПЛУ с матричной структурой
- 149. Организация ПЛУ с матричной структурой
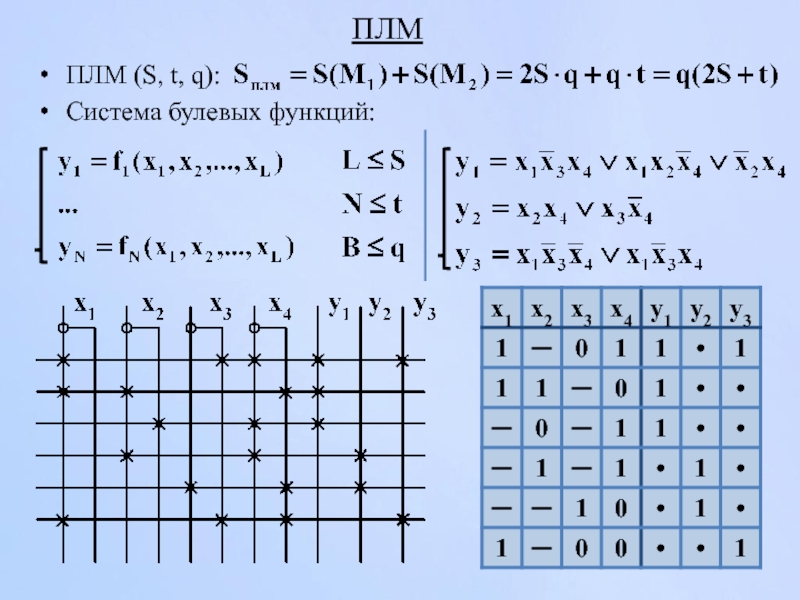
- 150. ПЛМ ПЛМ (S, t, q): Система булевых функций:
- 151. ПЗУ Дешифратор имеет 2s выходов
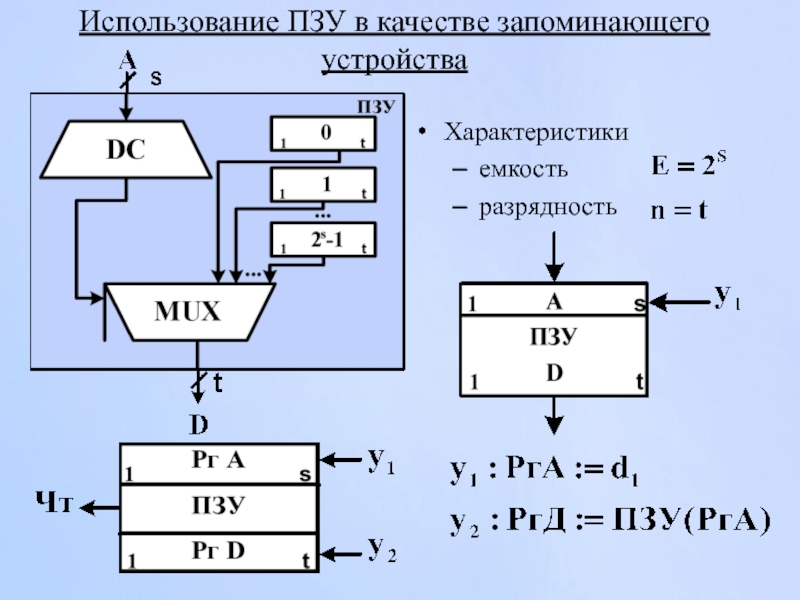
- 152. Использование ПЗУ в качестве запоминающего устройства Характеристики емкость разрядность
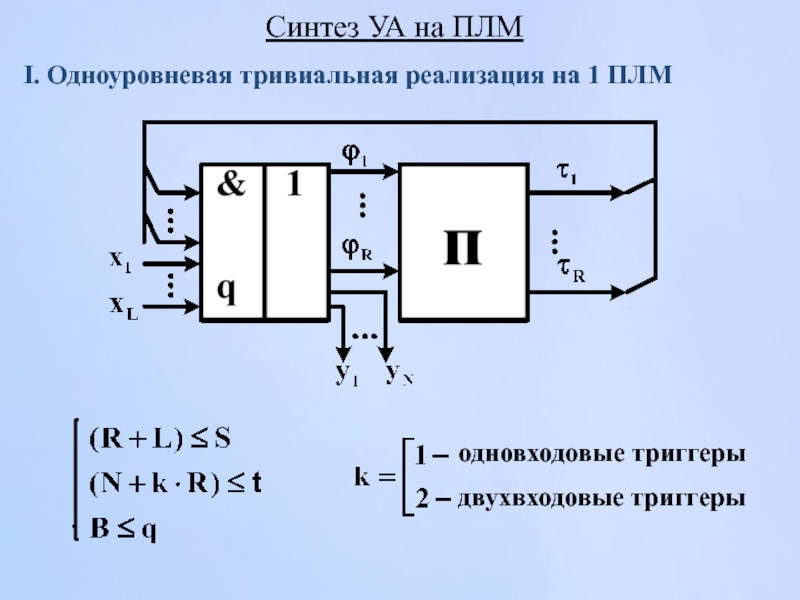
- 153. Синтез УА на ПЛМ I. Одноуровневая тривиальная
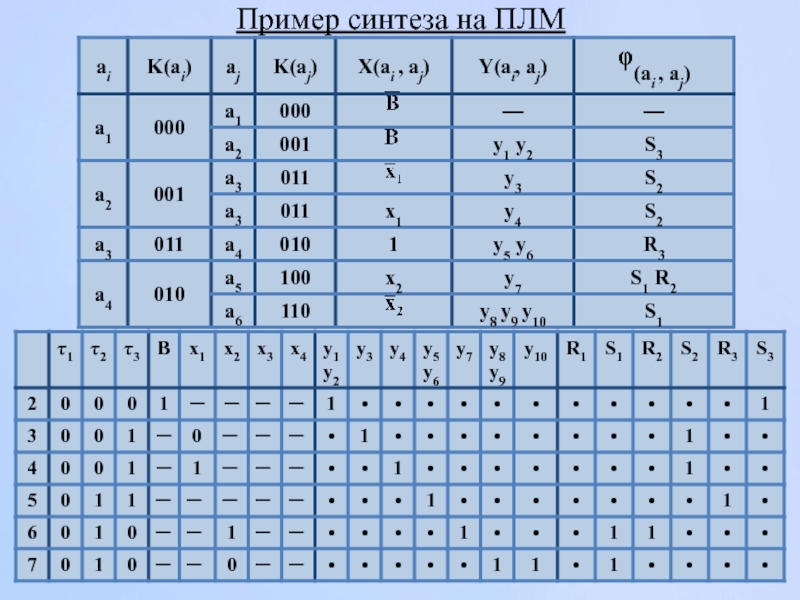
- 154. Пример синтеза на ПЛМ
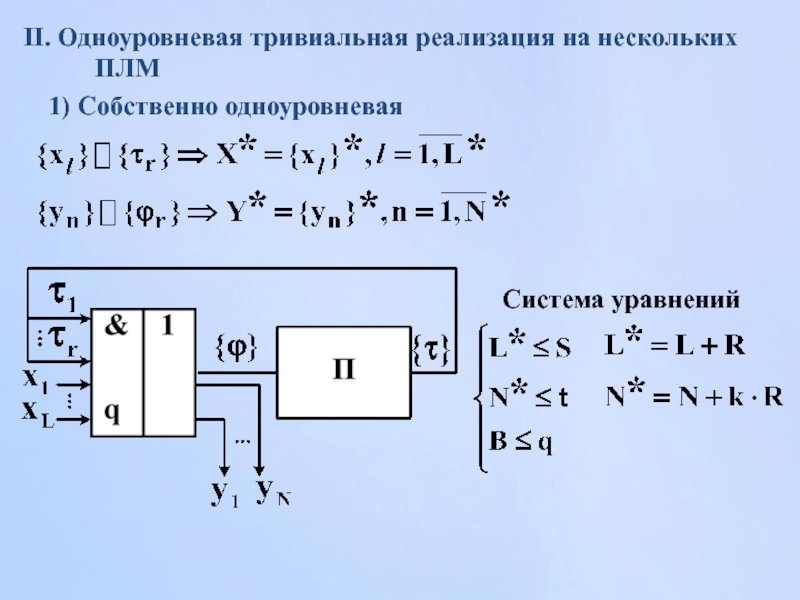
- 155. II. Одноуровневая тривиальная реализация на нескольких ПЛМ 1) Собственно одноуровневая Система уравнений
- 156. II. Одноуровневая тривиальная реализация на нескольких ПЛМ
- 157. II. Одноуровневая тривиальная реализация на нескольких ПЛМ
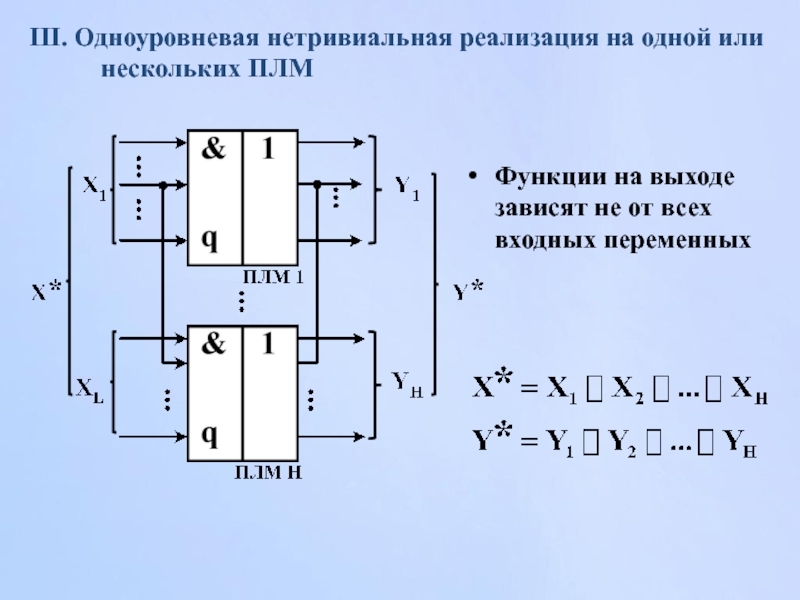
- 158. Функции на выходе зависят не от всех
- 159. Пример одноуровневой нетривиальной реализации ПЛМ (3, 2,
- 160. В КЧ автомата сигнал от входа к
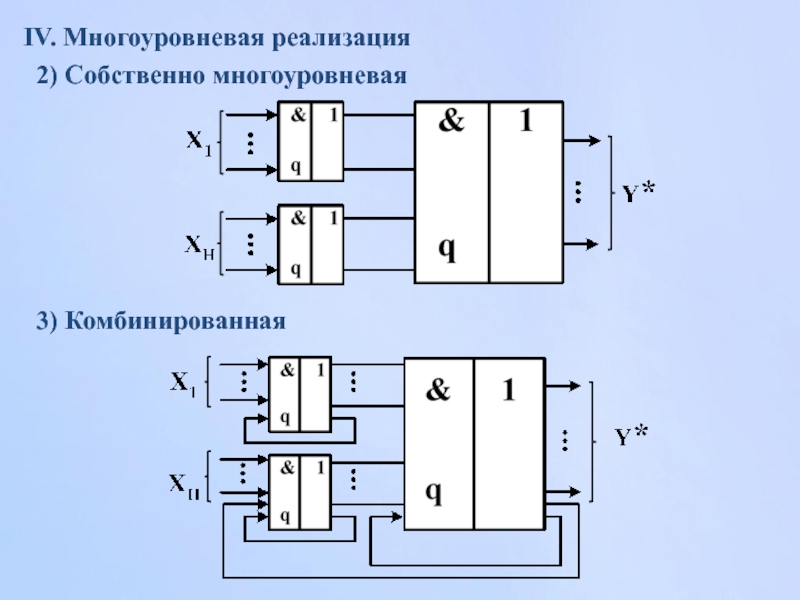
- 161. IV. Многоуровневая реализация 2) Собственно многоуровневая 3) Комбинированная
- 162. Устройство управления с программируемой логикой Структура микрокоманды
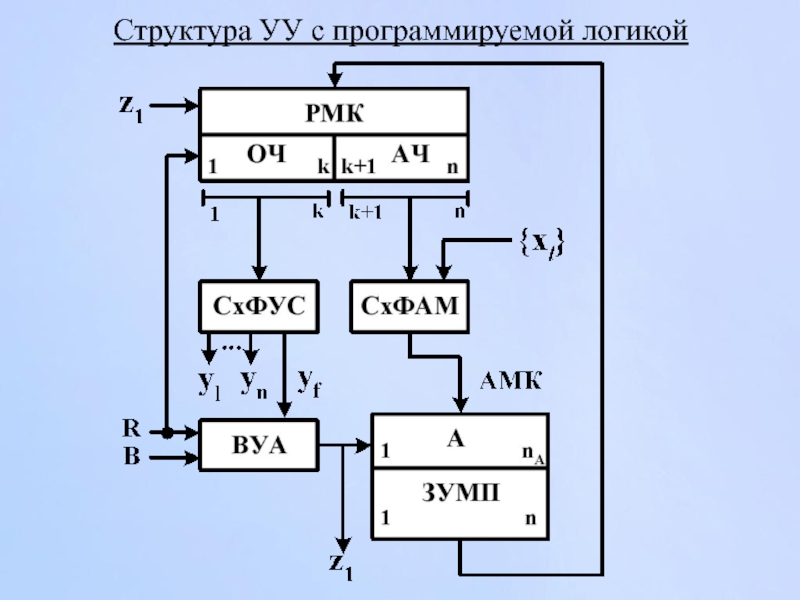
- 163. Структура УУ с программируемой логикой
- 164. Организация операционной части В общем случае ОЧ
- 165. Кодирование наборов микроопераций УА осуществляет кодирование микрокоманд,
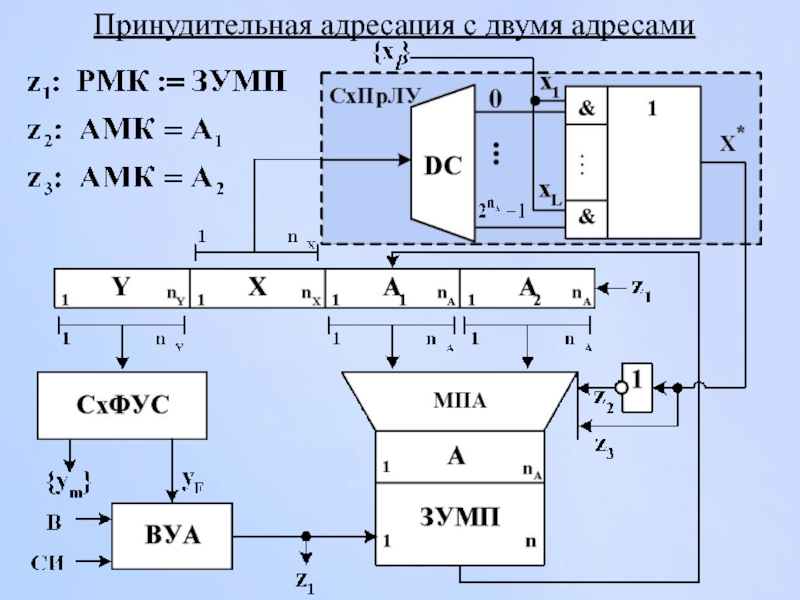
- 166. Способы организации адресной части (АЧ) автомата Принудительная адресация с двумя адресами
- 167. Принудительная адресация с двумя адресами
- 168. Мультиплексор – схема коммутации Р – общее число микрокоманд в микропрограмме – длина микропрограммы
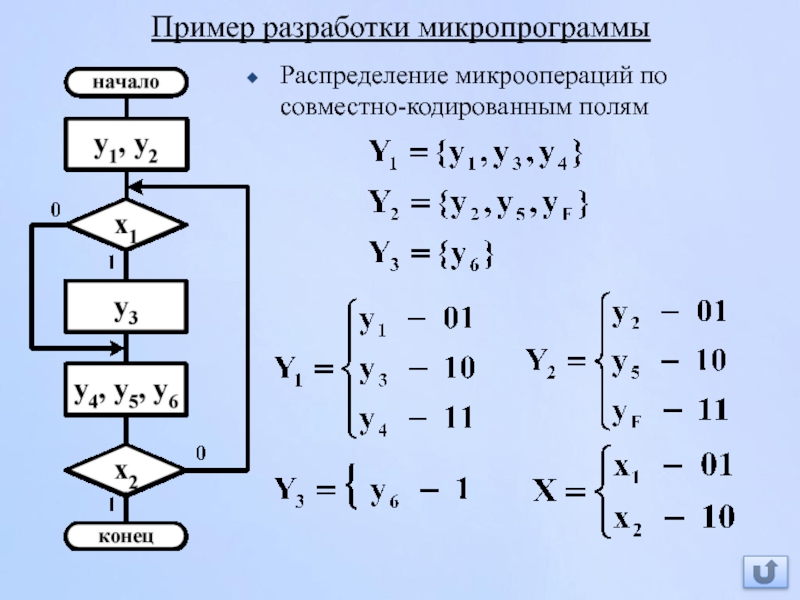
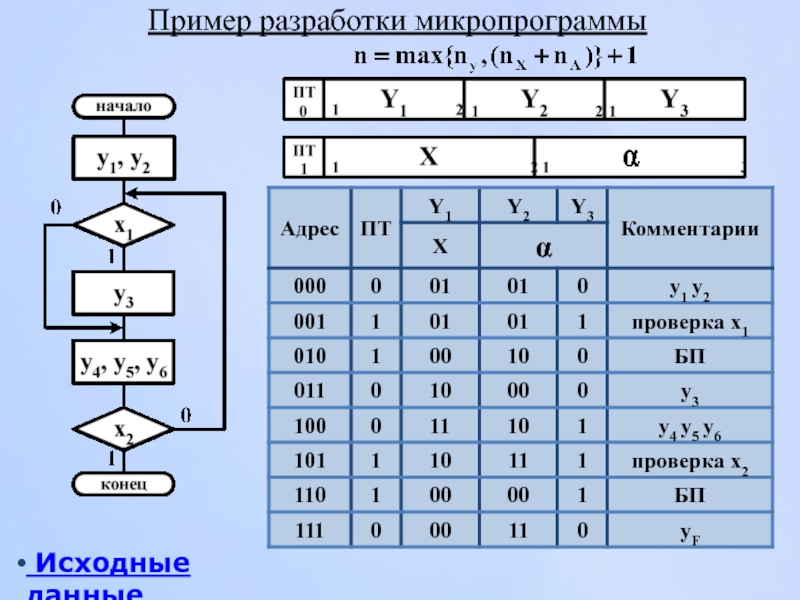
- 169. Пример разработки микропрограммы Распределение микроопераций по совместно-кодированным полям
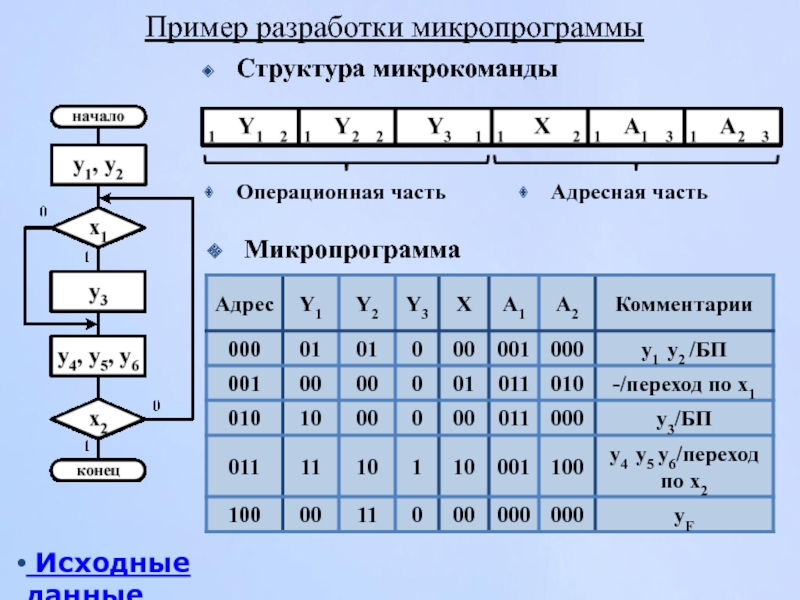
- 170. Пример разработки микропрограммы Микропрограмма Структура микрокоманды Операционная часть Адресная часть Исходные данные
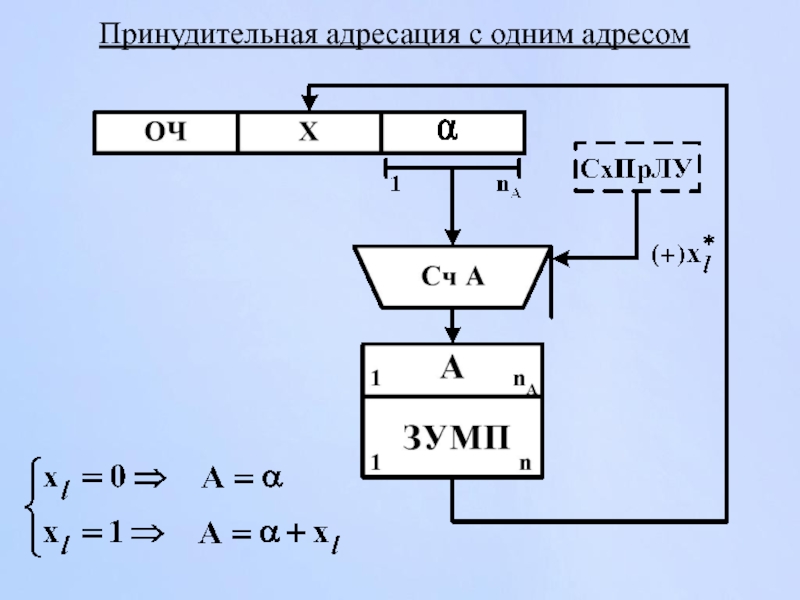
- 171. Принудительная адресация с одним адресом
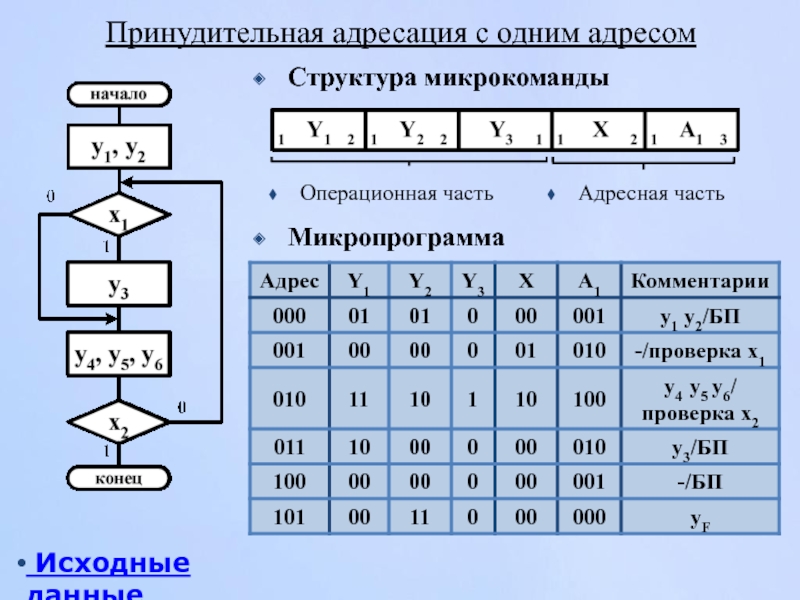
- 172. Принудительная адресация с одним адресом Микропрограмма
- 173. Используются для изменения естественного порядка следования микрокоманд
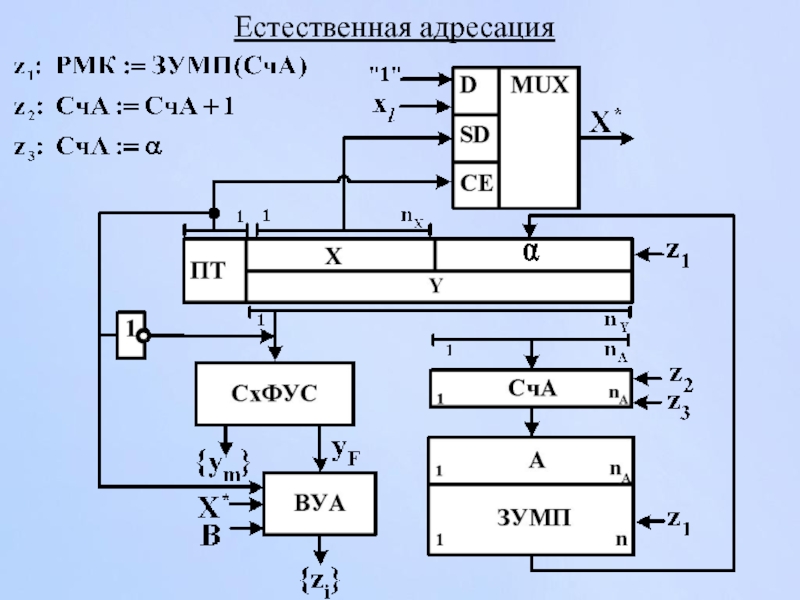
- 174. Естественная адресация
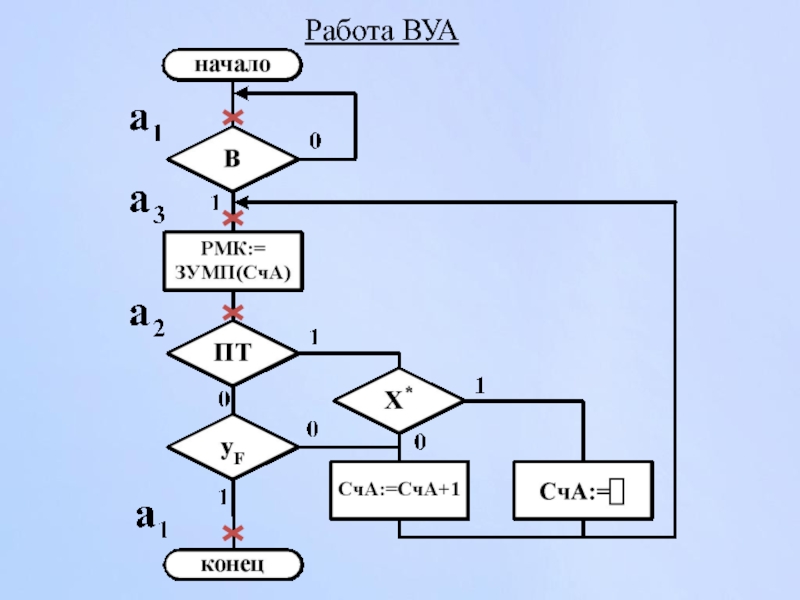
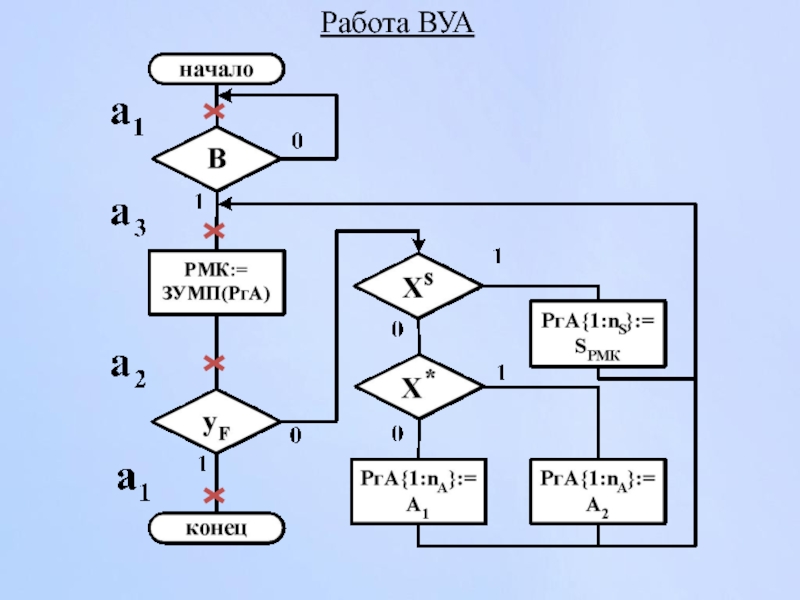
- 175. Работа ВУА
- 176. Пример разработки микропрограммы Исходные данные
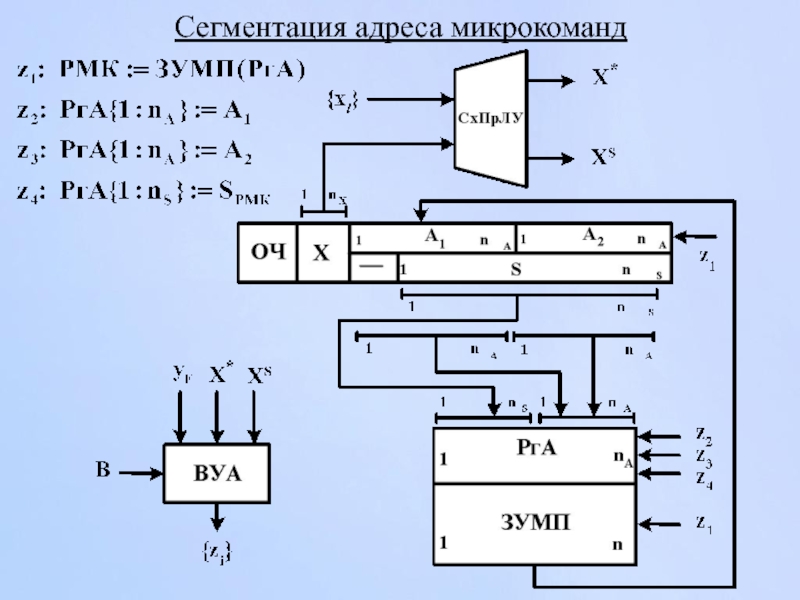
- 177. Сегментация адреса микрокоманд
- 178. Работа ВУА
Слайд 1Теория автоматов
Абстрактные цифровые автоматы
Структурные цифровые автоматы
Канонический метод структурного
Работа автомата и обеспечение устойчивости функционирования
Операционные устройства
Интерпретационный метод синтеза
Синтез УА на ПЛУ
УУ с программируемой логикой
Слайд 2Предмет теории автоматов
Теория автоматов ─ раздел теории управляющих систем, изучающий математические
Автомат
Некое устройство, выполняющее свои функции без участия человека (цифровые ─ устройства для преобразования цифровой информации).
Математическая модель реальных технических устройств. Как математическая модель, автомат рассматривается как чёрный ящик, имеющий конечное число входов и выходов и некоторое множество внутренних состояний, в которые он переходит практически мгновенно под действием входных сигналов.
Слайд 3 В ТА математические модели создаются с целью решения
Под анализом автомата понимают определение закона его функционирования при заданной структуре автомата.
Под синтезом – построение, проектирование автомата из более простых, элементарных автоматов по заданному закону функционирования.
Цель ТА:
изучение принципов построения и методов синтеза операционных устройств, представляемых в виде композиции операционного и управляющего автоматов и ориентированных на использование в вычислительной технике и устройствах автоматики.
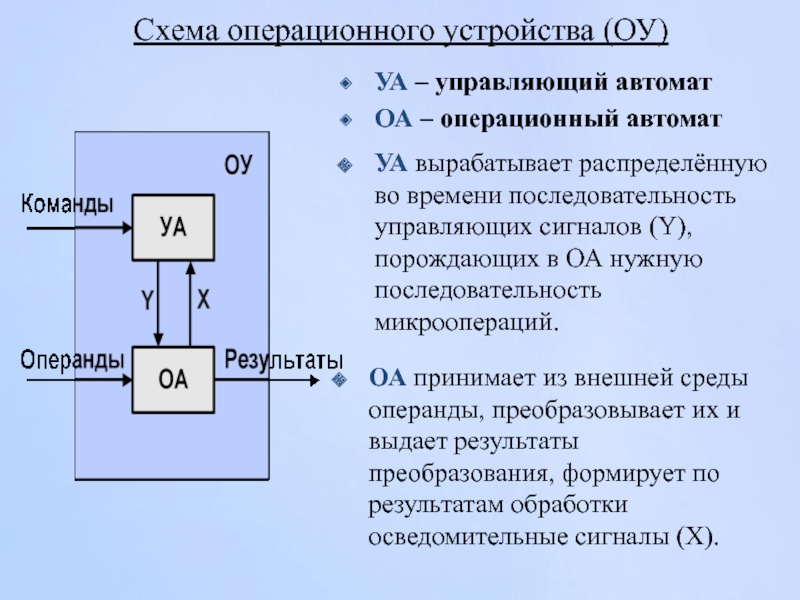
Слайд 4Схема операционного устройства (ОУ)
УА – управляющий автомат
ОА – операционный автомат
УА вырабатывает
ОА принимает из внешней среды операнды, преобразовывает их и выдает результаты преобразования, формирует по результатам обработки осведомительные сигналы (Х).
Слайд 5Абстрактные цифровые автоматы (АЦА)
АЦА - это математическая модель дискретного цифрового устройства
A - множество состояний автомата: А = {a1, … , аM}
Z - множество входных сигналов: Z = {z1, … , zF}
W - множество выходных сигналов: W = {w1, … , wG}
δ - функция переходов автомата. Определяет состояние автомата в следующий момент времени в зависимости от состояния am и входного сигнала zf в момент времени t :
as = δ (am, zf)
λ - функция выходов. Определяет выходной сигнал wg в зависимости от состояния am и входного сигнала zf :
wg = λ (am, zf)
aнач = a1 - начальное состояние автомата в начальный момент времени
Слайд 6 Цифровой автомат – математическая модель некоторого устройства, предназначенного для
Свойства ЦА:
дискретность входной информации;
дискретность выходной информации;
дискретность состояний;
дискретность времени;
конечность.
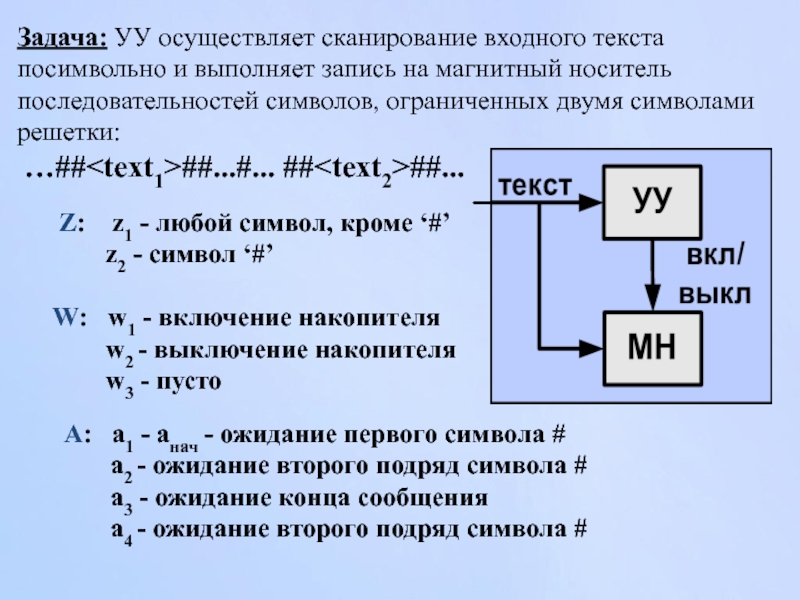
Слайд 7 Z: z1 - любой символ, кроме ‘#’
W: w1 - включение накопителя w2 - выключение накопителя w3 - пусто
Задача: УУ осуществляет сканирование входного текста посимвольно и выполняет запись на магнитный носитель последовательностей символов, ограниченных двумя символами решетки:
…## A: a1 - aнач - ожидание первого символа #
a2 - ожидание второго подряд символа #
a3 - ожидание конца сообщения
a4 - ожидание второго подряд символа #
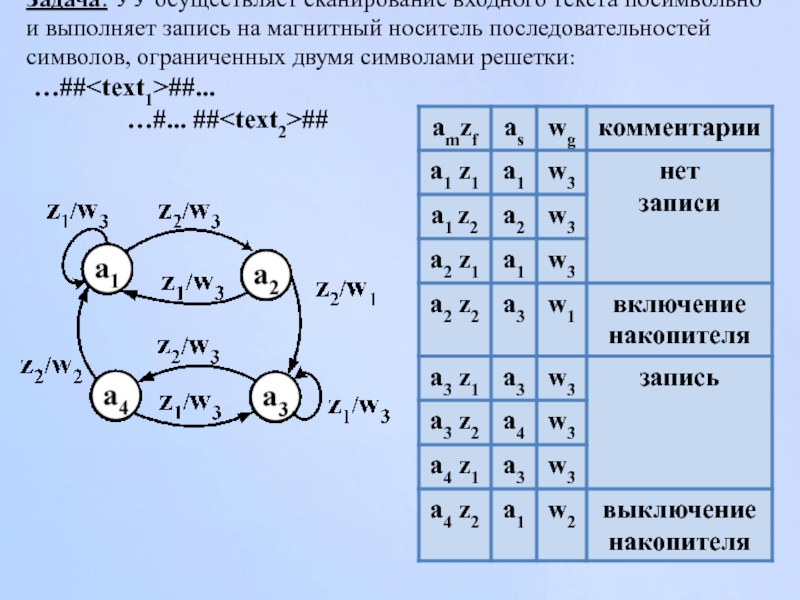
Слайд 8Задача: УУ осуществляет сканирование входного текста посимвольно и выполняет запись на
Слайд 9Классы абстрактных автоматов (АА)
Классификация АА по свойствам:
детерминированным называется автомат, для которого
вероятностный автомат – автомат, у которого функция переходов может принимать различные значения.
По свойствам входных/выходных сигналов и множеству состояний:
конечный – автомат, у которого множества A, Z, W конечные (счетные);
бесконечный – автомат, у которых хотя бы одно из множеств A, Z, W бесконечно.
as/p1 p1, p2 - вероятность
ak/p2 as, ak - состояния
δ (am, zf) =
Слайд 10По количеству различных состояний, в которых будет находиться АА:
с памятью –
тривиальный – имеет только одно состояние.
А={a1} => S*= (Z, W, λ)
λ - функция выхода, S* - комбинационная схема
По области определения функций переходов и выходов:
полностью определенный автомат, если функции переходов и выходов определены для всех возможных пар состояний и входных сигналов;
частичный - функции переходов и выходов определены не для всех пар состояний и входных сигналов.
По наличию начального состояния:
инициальный – для автомата определено начальное состояние;
неинициальный – автомат начинает свою работу из любого из возможных состояний.
Классы абстрактных автоматов
Слайд 11По устойчивости состояний:
асинхронный автомат - все состояния устойчивы;
синхронный - если существует
Устойчивое состояние автомата - если при поступлении любого входного сигнала, вызывающего переход в это состояние, автомат остается в том же самом состоянии.
δ (am, zf) = as
δ (as, zf) = as
Неустойчивое состояние (существует риск проскока). δ (am, zf) = as
δ (as, zf) = ak
Классы абстрактных автоматов
Слайд 12Автомат Мили (Mealy)
Выходной сигнал зависит и от состояния и от входного
w (t) = λ (a(t), z(t))
a(t+1)= δ (a(t), z(t))
Автомат Мура (Moore)
Выходной сигнал в текущий момент зависит только от состояния
w (t) = λ (a(t))
a(t+1)= δ (a(t),z(t))
Классификация АА по способу формирования выходных сигналов
Слайд 13Модель С-автомата
Имеет 2 выходных канала: по одному формируются выходные сигналы автомата
a (t+1) = δ (a(t), z(t))
w (t) = λ1 (a(t), z(t))
u (t) = λ2 (a(t))
Выходной сигнал I рода
Выходной сигнал II рода
Слайд 14 Языки задания АА
Начальные языки
Автоматные языки
Способы явного задания
переходов и выходов
Табличный
Графический
Матричный
Слайд 15Табличный способ задания
Таблица выходов
Таблица переходов
Совмещенная таблица переходов и выходов для автомата
δ:
λ:
δ/λ:
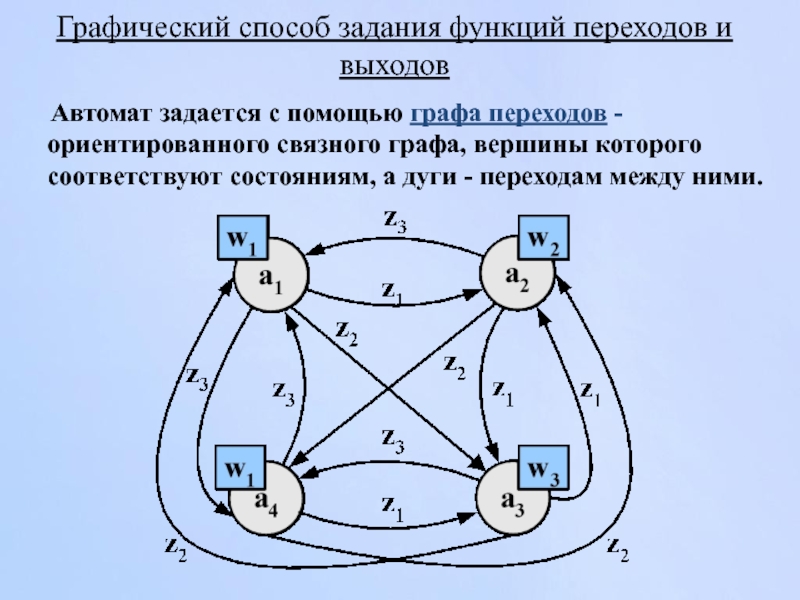
Слайд 17Графический способ задания функций переходов и выходов
Автомат задается
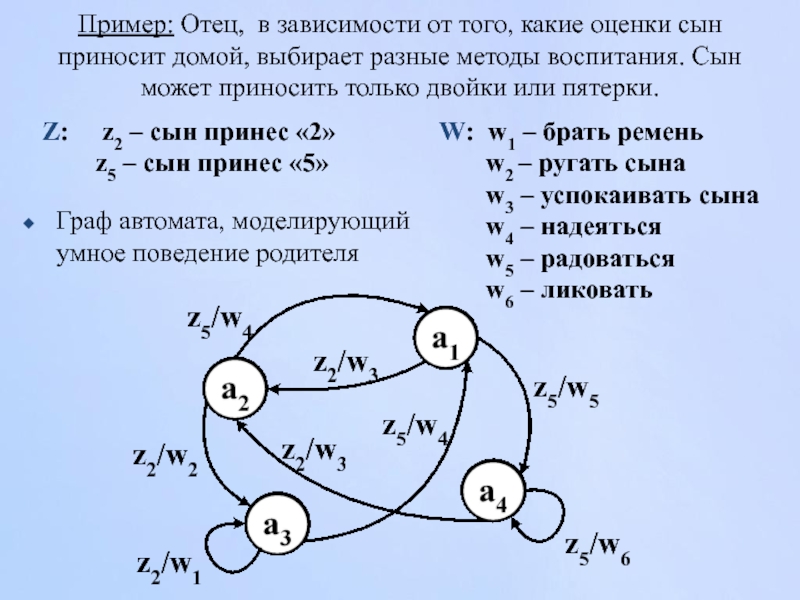
Слайд 18Пример: Отец, в зависимости от того, какие оценки сын приносит домой,
Z: z2 – сын принес «2»
z5 – сын принес «5»
W: w1 – брать ремень
w2 – ругать сына
w3 – успокаивать сына
w4 – надеяться
w5 – радоваться
w6 – ликовать
Граф автомата, моделирующий умное поведение родителя
z5/w4
z5/w5
z5/w6
z2/w1
z2/w2
z2/w3
z5/w4
z2/w3
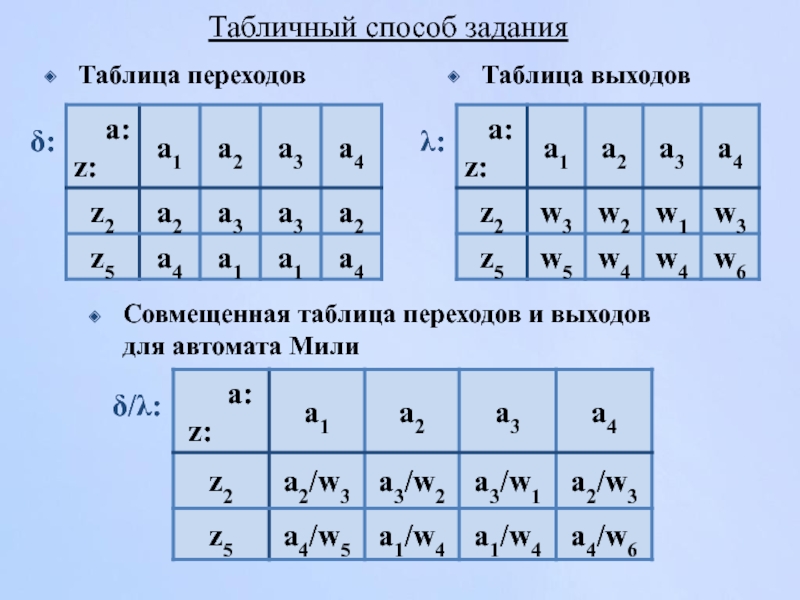
Слайд 19Табличный способ задания
δ:
λ:
Совмещенная таблица переходов и выходов для автомата Мили
δ/λ:
Таблица выходов
Таблица
Слайд 20Матричный способ задания
Матрица связей для автомата Мили
Матрицы, описывающие автомат Мура
Матрица соединений
Матрица-столбец
Слайд 21Преобразование автомата Мура в автомат Мили
S1 = (Z1, W1, A1, δ1,
S2 = (Z2, W2, A2, δ 2, λ 2, a12 ) - автомат Мили
Z2 = Z1
W2 = W1
Эквивалентные автоматы
Для эквивалентности требуется, чтобы реакции на любую входную последовательность совпадали:
выбираем множество состояний исходного автомата
A2 = A1;
в качестве функций переходов берем ту же функцию δ2= δ1;
в качестве начального состояния - то же состояние a12= a11.
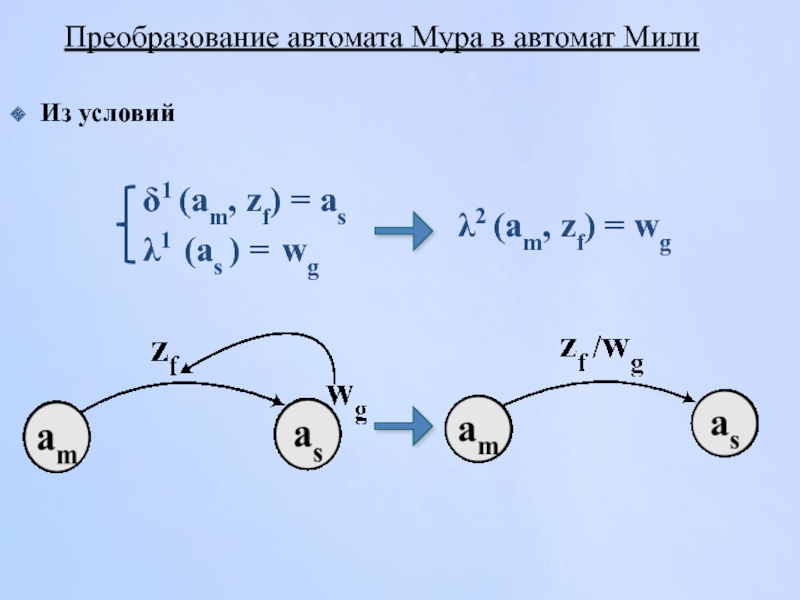
Слайд 22Преобразование автомата Мура в автомат Мили
Из условий
λ2 (am, zf) =
δ1 (am, zf) = as
λ1 (as ) = wg
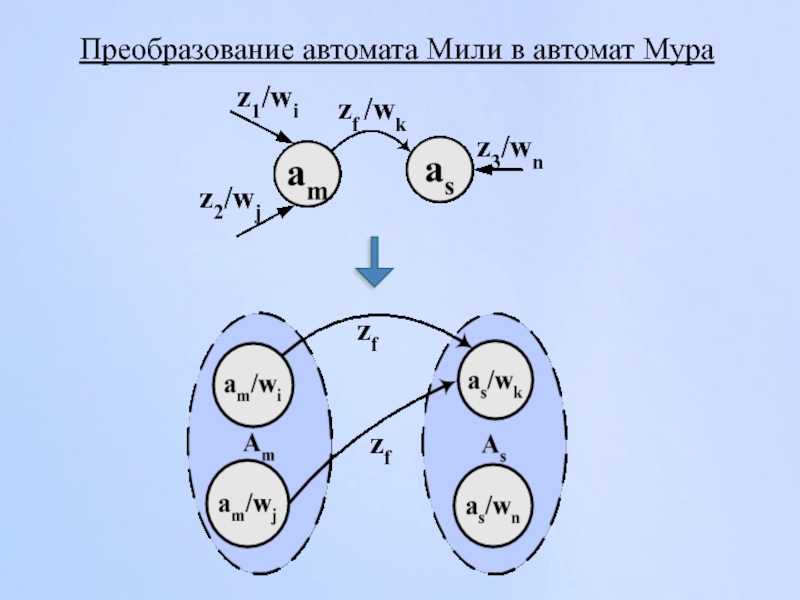
Слайд 23Преобразование автомата Мили в автомат Мура
Каждому состоянию автомата Мили A1 поставлено
As = {(as,w1),(as,w2),(as,w3)}
δ1 (am, zf) = as
λ1 (am, zf) = ws
S1 = (Z1, W1, A1, δ1, λ1, a11 ) - автомат Мили
S2 = (Z2, W2, A2, δ 2, λ 2, a12 ) - автомат Мура
Z2 = Z1
W2 = W1
Эквивалентные автоматы
Слайд 25Эквивалентность автоматов
Автоматы с одинаковыми наборами входных и выходных сигналов называются эквивалентными,
Совмещенная таблица переходов и выходов автомата Мили S1
Отмеченная таблица переходов автомата Мура S2
Слайд 26Задача минимизации АА
Задача нахождения автомата с минимальным числом внутренних состояний в
Два автомата одного типа эквивалентны, если для каждого состояния am первого автомата существует эквивалентное состояние ak второго автомата и наоборот
Два состояния эквивалентны, если для всевозможных входных слов реакции автоматов в этих состояниях совпадают
SA=SB
MA≠MB
= . . .
Класс
эквивалентных
состояний
Слайд 27Структурные цифровые автоматы (СЦА)
СЦА описывает реальное устройство как сложный объект, состоящий
Задание СЦА
описание поведения и свойств элементарных автоматов;
задание схемы соединения автоматов между собой.
Особенности задания СЦА
наличие нескольких входных/выходных каналов;
работа со структурными входными/выходными дискретными сигналами;
определение состояния автомата, как набора состояний составляющих СЦА элементарных автоматов.
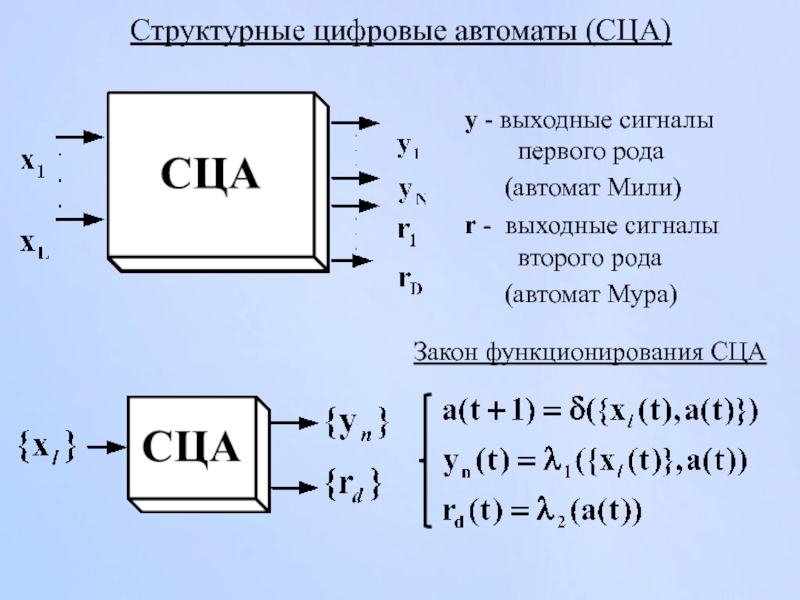
Слайд 28y - выходные сигналы первого рода
(автомат Мили)
r -
(автомат Мура)
Закон функционирования СЦА
Структурные цифровые автоматы (СЦА)
Слайд 29Установление соответствия абстрактных и структурных сигналов
Установление соответствия абстрактных и структурных сигналов
выбрать количество структурных каналов;
закодировать абстрактные сигналы в структурные.
Определение количества каналов:
L ≥ log2F = ] log2F [ F - число абстрактных входных сигналов
N ≥ log2G = ] log2G [ G - число абстрактных выходных сигналов первого рода
D ≥ log2H = ] log2H [ H - число абстрактных выходных сигналов второго рода
Кодирование сигналов:
произвольное;
оптимизирующее:
уменьшающее затраты оборудования;
обеспечивающее устойчивость функционирования.
Слайд 30Пример установления соответствия между сигналами
Определение количества каналов (разрядности входных/выходных сигналов)
Z =
W = {w1, w2, w3, w4, w5}
U = {u1, u2, u3, u4}
L = ] log23 [ = 2
N = ] log25 [ = 3
D = ] log24 [ = 2
Произвольное кодирование
Слайд 31Методы структурного синтеза ЦА
Основой всех методов является каноническая
структура ЦА
Канонический метод
Графический метод структурного синтеза.
Интерпретационный метод структурного синтеза.
Группа методов структурного синтеза, ориентированных на использование больших интегральных схем (БИС).
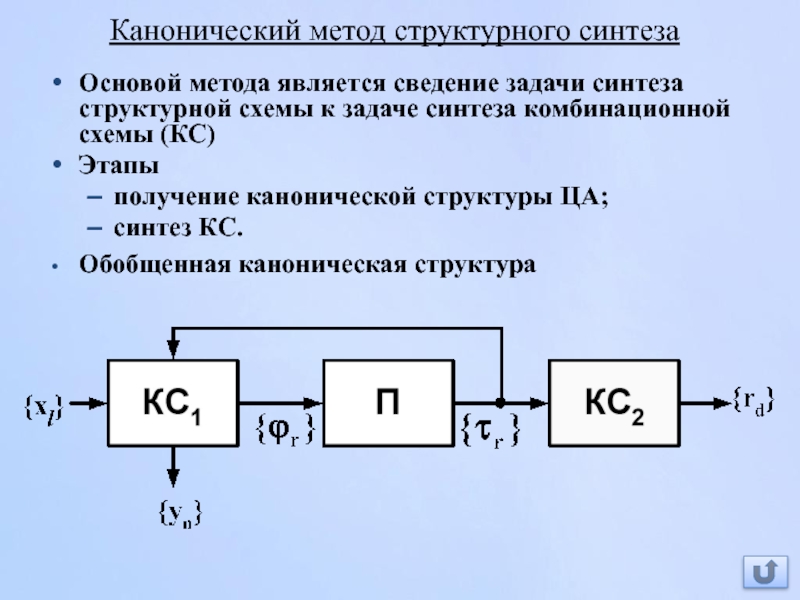
Слайд 32Канонический метод структурного синтеза
Основой метода является сведение задачи синтеза структурной схемы
Этапы
получение канонической структуры ЦА;
синтез КС.
Обобщенная каноническая структура
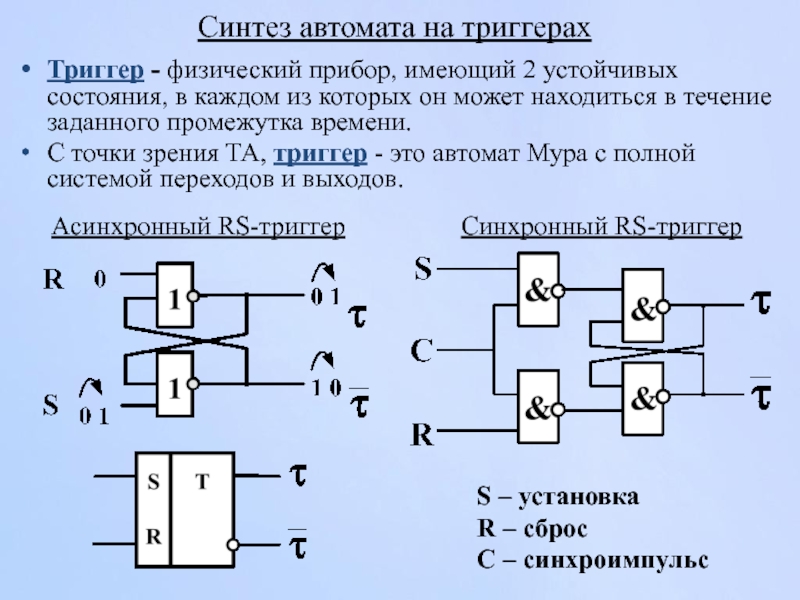
Слайд 34Синтез автомата на триггерах
Триггер - физический прибор, имеющий 2 устойчивых состояния,
С точки зрения ТА, триггер - это автомат Мура с полной системой переходов и выходов.
Синхронный RS-триггер
Асинхронный RS-триггер
S – установка
R – сброс
С – синхроимпульс
Слайд 35Виды стандартных триггеров
По логике работы и количеству входов различают следующие стандартные
D-триггер - триггер-задержка;
T-триггер - со счетным входом;
RS-триггер - с раздельными входами установки и сброса;
JK-триггер - универсальный с раздельными входами установки и сброса.
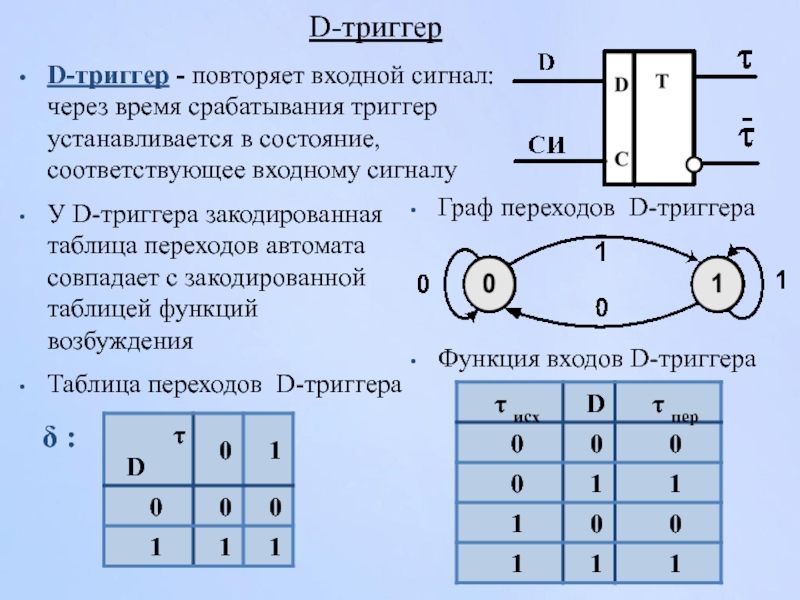
Слайд 36D-триггер
D-триггер - повторяет входной сигнал: через время срабатывания триггер устанавливается в
δ :
У D-триггера закодированная таблица переходов автомата совпадает с закодированной таблицей функций возбуждения
Таблица переходов D-триггера
Граф переходов D-триггера
Функция входов D-триггера
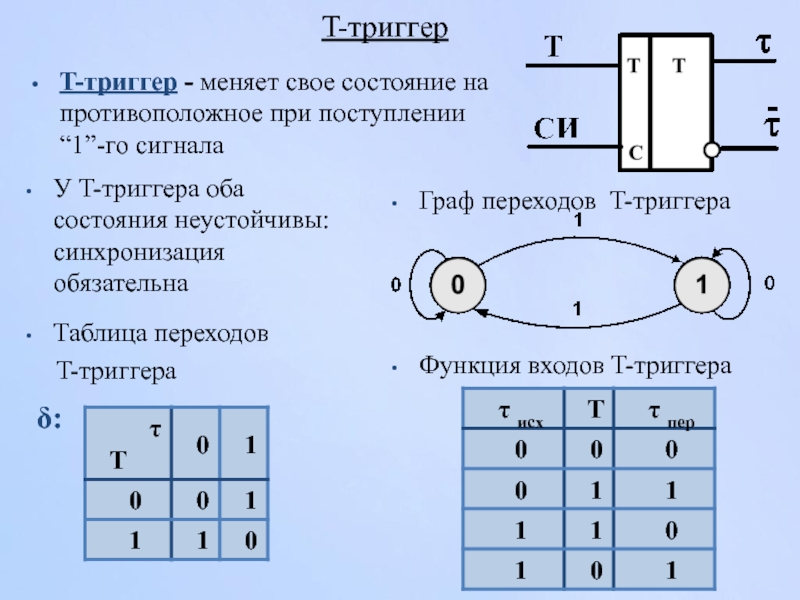
Слайд 37T-триггер - меняет свое состояние на противоположное при поступлении “1”-го сигнала
δ:
У
Таблица переходов
T-триггера
Граф переходов T-триггера
Функция входов T-триггера
T-триггер
Слайд 40Минимизация комбинационной части автомата
Цель минимизации
уменьшение затрат оборудования при последующей реализации канонических
Основные направления минимизации
классическая (в классе нормальных форм) по СДНФ получаем МДНФ;
доопределение функций с целью их последующей минимизации;
получение абсолютно минимальных форм.
Слайд 41Классическая минимизация
СДНФ(СКНФ) => МДНФ(МКНФ)
Нормальная форма
ДНФ => МДНФ
ДНФ => СДНФ => МДНФ
Минимизации
Чаще всего для минимизации булевых функций используются карты Карно или диаграммы Вейча
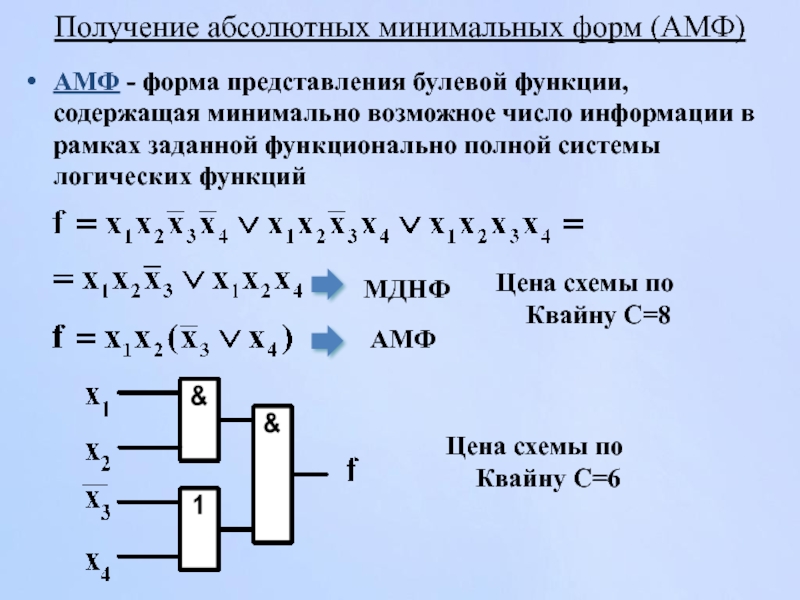
Слайд 42Получение абсолютных минимальных форм (АМФ)
АМФ - форма представления булевой функции, содержащая
МДНФ
Цена схемы по Квайну С=8
Цена схемы по Квайну С=6
АМФ
Слайд 45Кодирование сигналов и состояний
Сложность комбинационной части автомата
Сложность КЧ автомата
Кодирование выходных сигналов, уменьшающее сложность КС
для каждого выходного сигнала подсчитывается число появлений в таблице выходов
выходные сигналы упорядочиваются по убыванию частоты их появления в таблице выходов
поставить в соответствие выходным сигналам коды: сначала “0” код, затем коды, содержащие одну “1”, затем коды, содержащие две “1” и т.д.
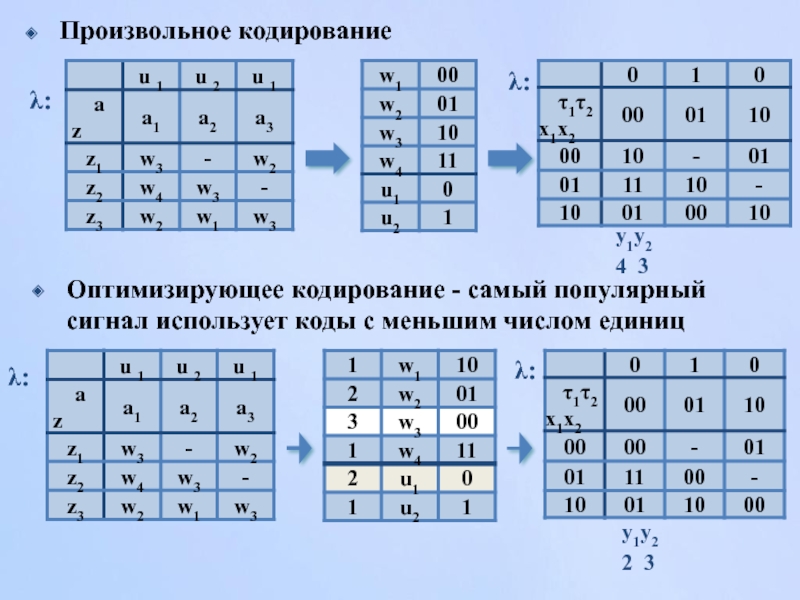
Слайд 46y1y2
4 3
Произвольное кодирование
y1y2
2 3
Оптимизирующее кодирование - самый популярный сигнал использует коды
λ:
λ:
λ:
λ:
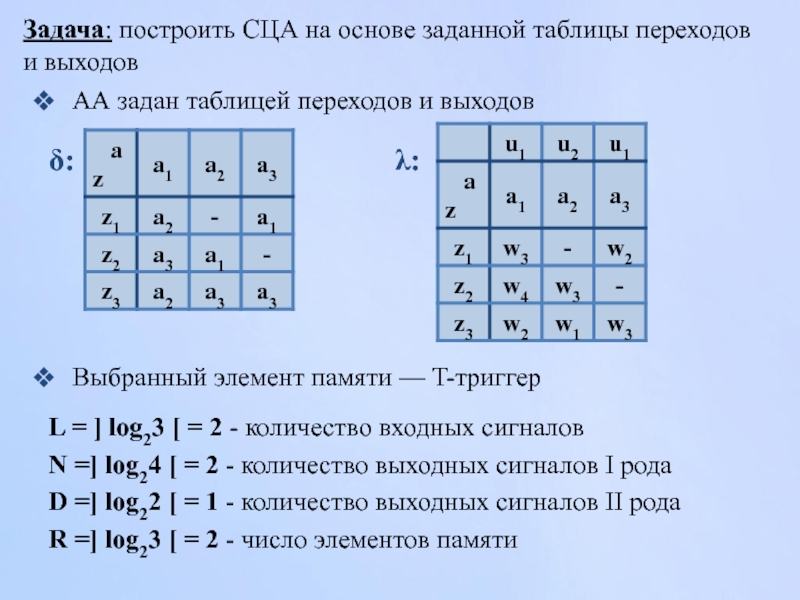
Слайд 47Задача: построить СЦА на основе заданной таблицы переходов и выходов
АА задан
Выбранный элемент памяти — T-триггер
L = ] log23 [ = 2 - количество входных сигналов
N =] log24 [ = 2 - количество выходных сигналов I рода
D =] log22 [ = 1 - количество выходных сигналов II рода
R =] log23 [ = 2 - число элементов памяти
λ:
δ:
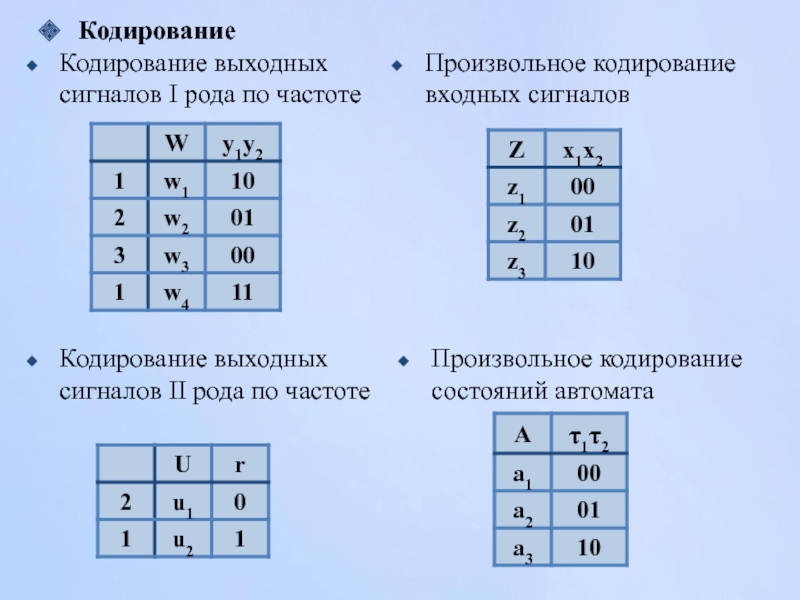
Слайд 48Кодирование
Кодирование выходных сигналов I рода по частоте
Кодирование выходных сигналов II рода
Произвольное кодирование входных сигналов
Произвольное кодирование состояний автомата
Слайд 49 τ1τ2
x1x2 00 01 11 10
00
11
10
τ1τ2
x1x2 00 01 11 10
00
01
11
10
Закодированная таблица выходов
λ:
y1y2
2 3
Карта Карно для выходных сигналов
Система канонических уравнений для выходных сигналов
y1:
y2:
α1
α2
α1
α3
α4
r:
τ1
τ2 0 1
0
1
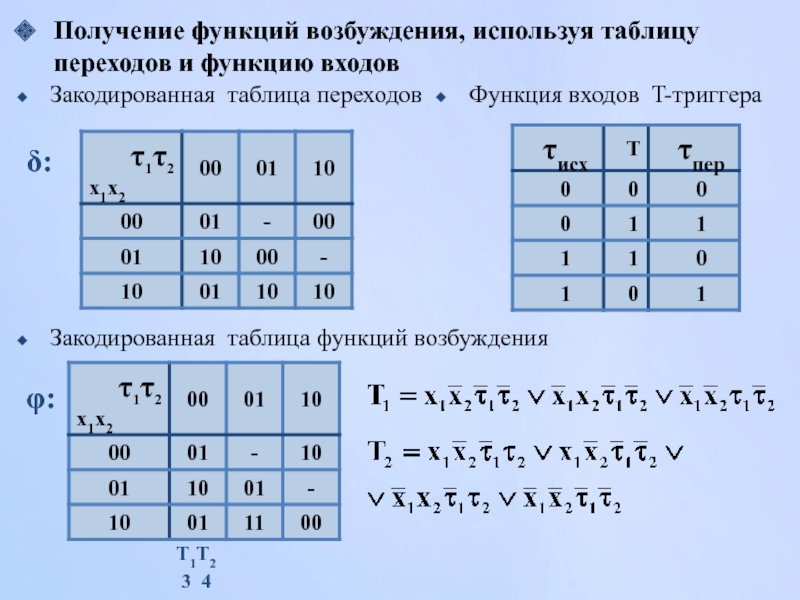
Слайд 50Получение функций возбуждения, используя таблицу переходов и функцию входов
δ:
Функция входов
Закодированная таблица переходов
Закодированная таблица функций возбуждения
φ:
T1T2
3 4
Слайд 51 τ1τ2
x1x2 00 01
00
01
11
10
τ1τ2
x1x2 00 01 11 10
00
01
11
10
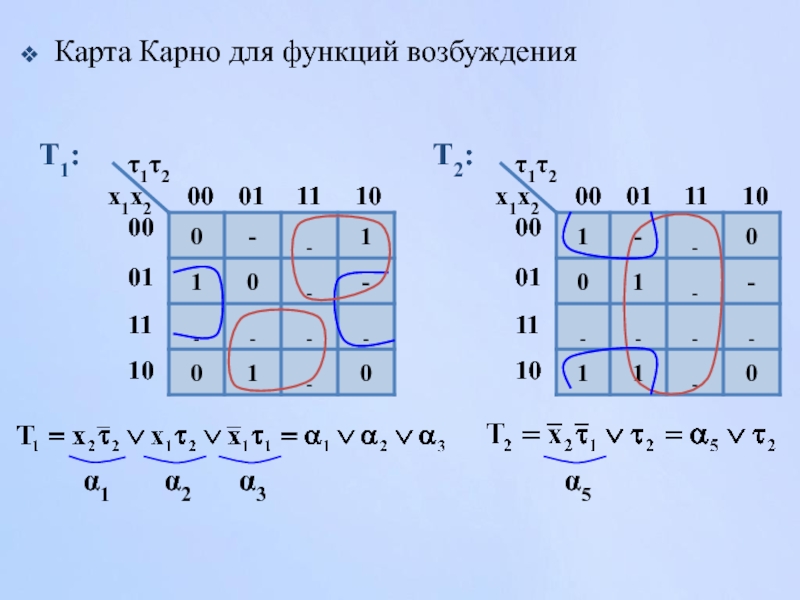
Карта Карно для функций возбуждения
T1:
T2:
α2
α1
α3
α5
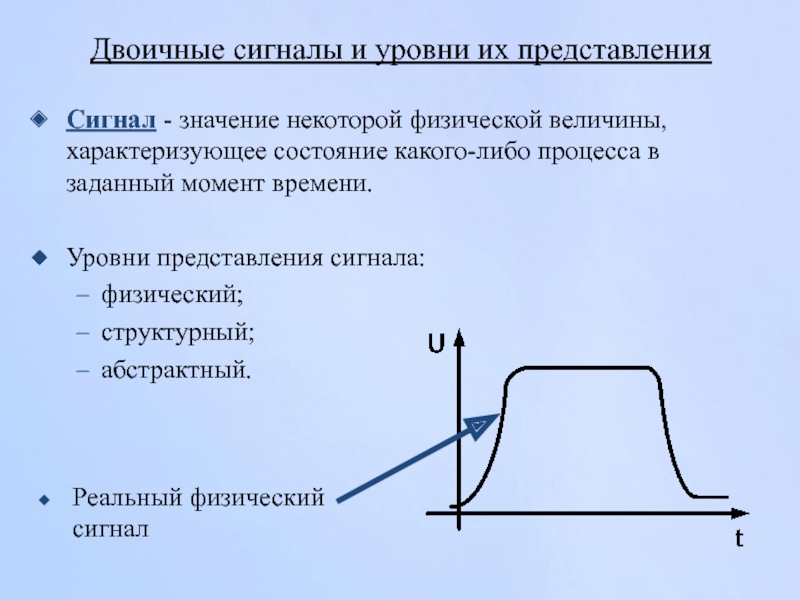
Слайд 55Двоичные сигналы и уровни их представления
Сигнал - значение некоторой физической величины,
Уровни представления сигнала:
физический;
структурный;
абстрактный.
Реальный физический сигнал
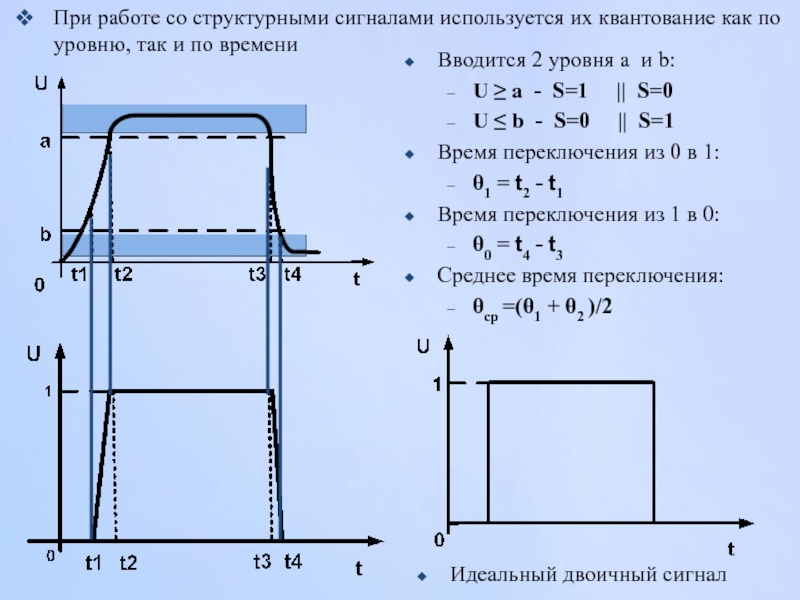
Слайд 56При работе со структурными сигналами используется их квантование как по уровню,
Вводится 2 уровня a и b:
U ≥ a - S=1 || S=0
U ≤ b - S=0 || S=1
Время переключения из 0 в 1:
θ1 = t2 - t1
Время переключения из 1 в 0:
θ0 = t4 - t3
Среднее время переключения:
θср =(θ1 + θ2 )/2
Идеальный двоичный сигнал
Слайд 58Распространение сигнала в схеме
сигнал в реальной схеме всегда распространяется с задержкой,
Распространение сигнала в схеме
τ0 θ0
τ0 θ0
τ1 θ1
Слайд 60Синхронизация
Под синхронизацией ЦА понимается управление моментами смены состояния устройства с помощью
Цель введения синхронизации
обеспечение правильного взаимодействия цифровых автоматов между собой по входу-выходу
обеспечение устойчивости функционирования ЦА
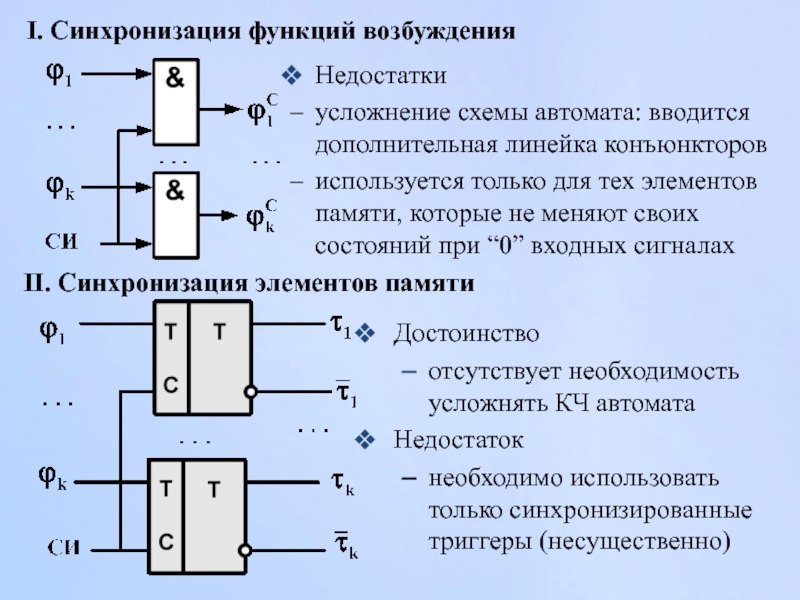
Слайд 62Достоинство
отсутствует необходимость усложнять КЧ автомата
Недостаток
необходимо использовать только синхронизированные триггеры (несущественно)
II. Синхронизация
I. Синхронизация функций возбуждения
Недостатки
усложнение схемы автомата: вводится дополнительная линейка конъюнкторов
используется только для тех элементов памяти, которые не меняют своих состояний при “0” входных сигналах
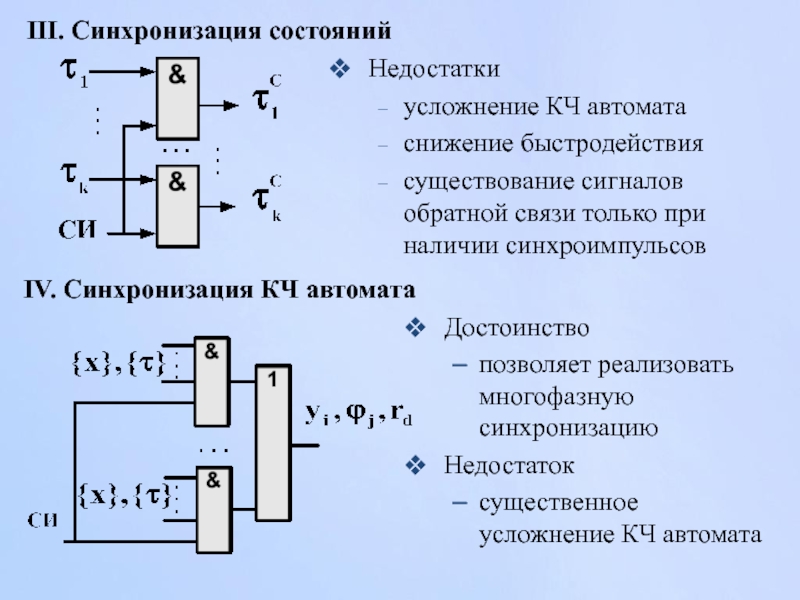
Слайд 63Достоинство
позволяет реализовать многофазную синхронизацию
Недостаток
существенное усложнение КЧ автомата
IV. Синхронизация КЧ автомата
III. Синхронизация
Недостатки
усложнение КЧ автомата
снижение быстродействия
существование сигналов обратной связи только при наличии синхроимпульсов
Слайд 64Факторы неустойчивой работы ЦА
Неодновременное поступление входных сигналов.
Неустойчивость состояний.
«Гонки» («состязания») в
Источники неустойчивости работы ЦА
Взаимодействия с другими автоматами по входу-выходу.
Особенности работы самого ЦА (синхронные и асинхронные автоматы).
Различные задержки распространения сигналов в схеме.
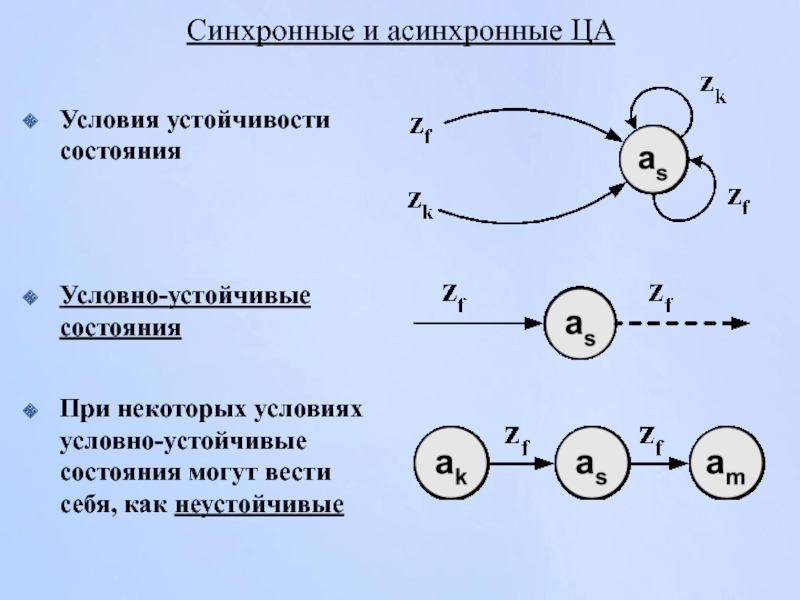
Слайд 65Синхронные и асинхронные ЦА
Условно-устойчивые состояния
При некоторых условиях условно-устойчивые состояния могут
Условия устойчивости состояния
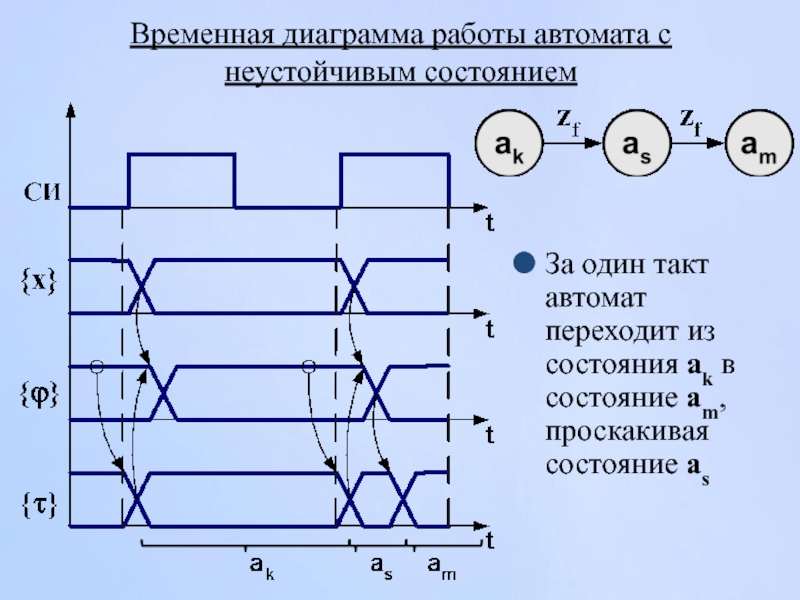
Слайд 66Временная диаграмма работы автомата с неустойчивым состоянием
За один такт автомат переходит
Слайд 67Работа асинхронного автомата без введения синхронизации
Рассматриваем
С-автомат
с канонической структурой
обеспечена устойчивость функционирования автомата
смена
подача входных сигналов осуществляется в начале каждого следующего такта
Обобщенная каноническая структура
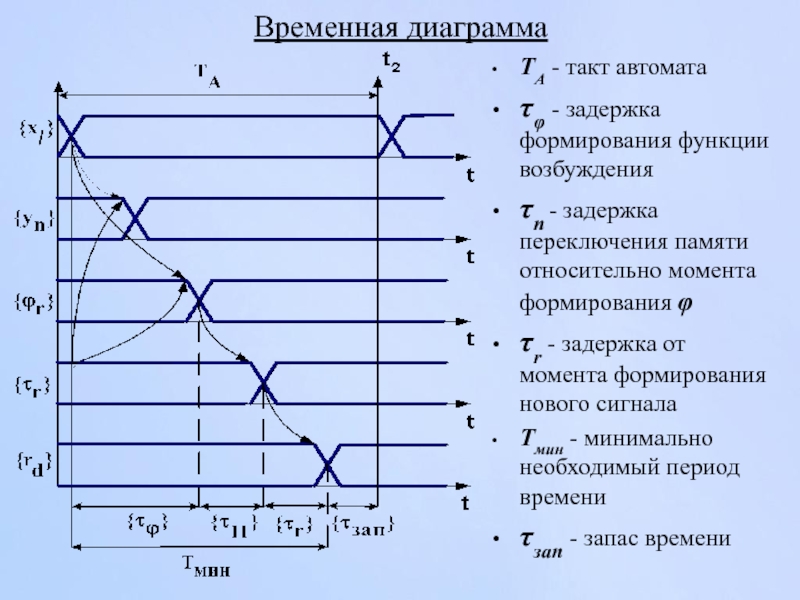
Слайд 68Временная диаграмма
ТА - такт автомата
τφ - задержка формирования функции возбуждения
τп -
τr - задержка от момента формирования нового сигнала
Тмин - минимально необходимый период времени
τзап - запас времени
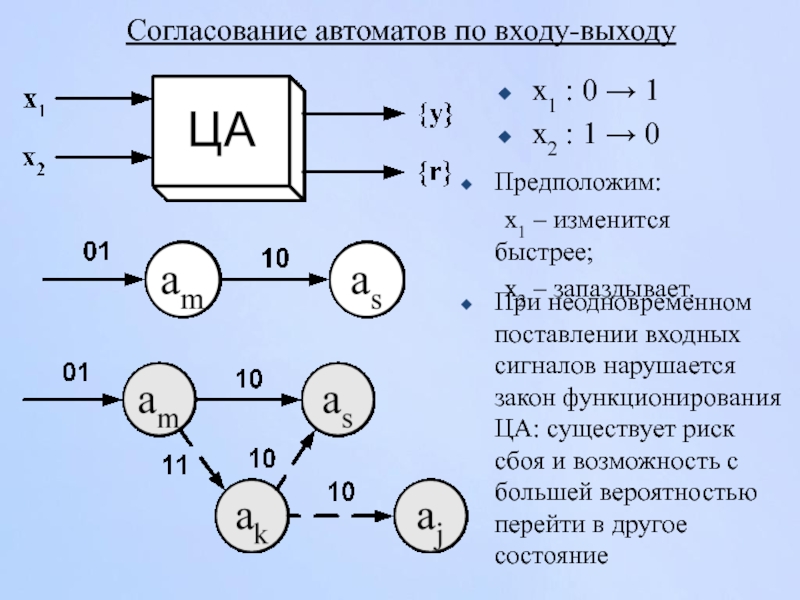
Слайд 69Согласование автоматов по входу-выходу
x1 : 0 → 1
x2 : 1 →
Предположим:
x1 – изменится быстрее;
x2 – запаздывает.
При неодновременном поставлении входных сигналов нарушается закон функционирования ЦА: существует риск сбоя и возможность с большей вероятностью перейти в другое состояние
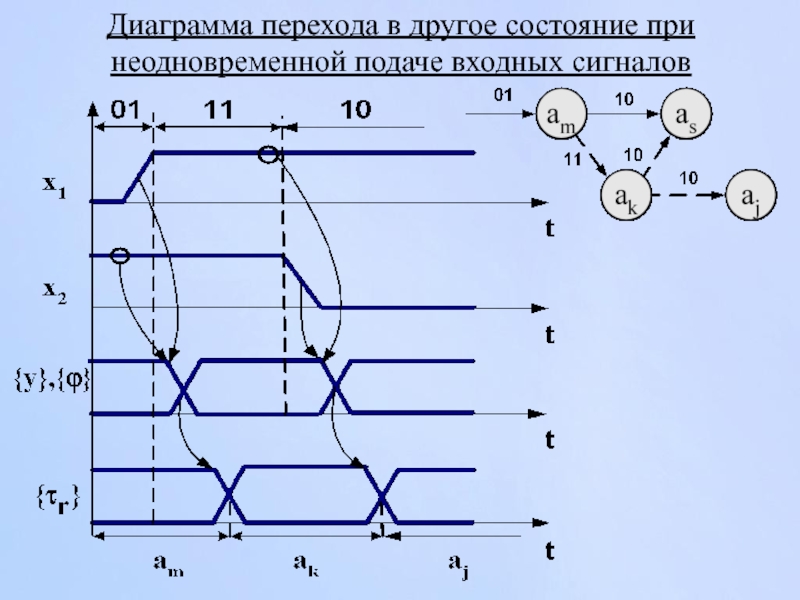
Слайд 71Причины нарушения
Наличие разброса моментов переключения входных сигналов
Влияние функций переходов автомата
Различные
Правильная работа ЦА при неодновременном поступлении входных сигналов обеспечивается введением синхронизации в схему автомата
Слайд 72Методы обеспечения устойчивости состояний
Ограничить длительность синхроимпульса – импульсная синхронизация
Многофазная синхронизация, то
Использование двухступенчатых элементов памяти
Использование элементов памяти (триггеров) с динамическим управлением по входу синхронизации
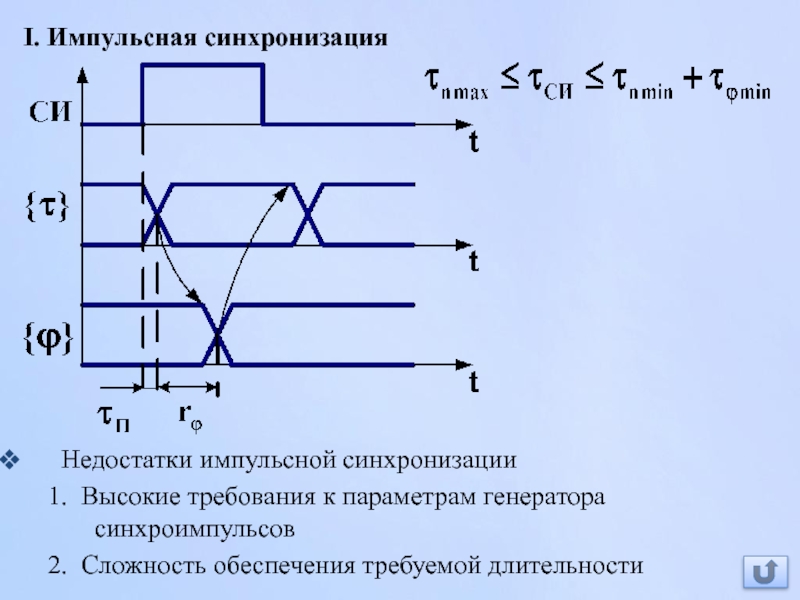
Слайд 73I. Импульсная синхронизация
Недостатки импульсной синхронизации
1. Высокие требования к параметрам генератора синхроимпульсов
2. Сложность обеспечения требуемой длительности
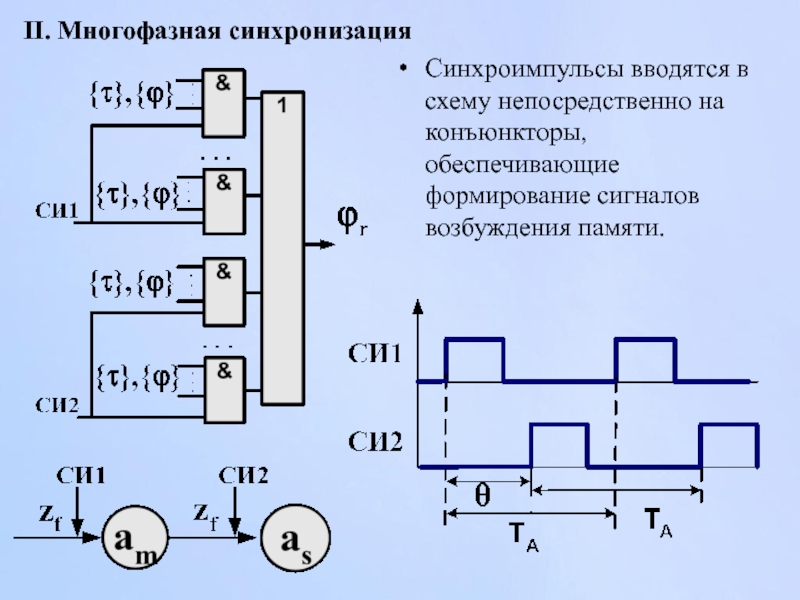
Слайд 74II. Многофазная синхронизация
Синхроимпульсы вводятся в схему непосредственно на конъюнкторы, обеспечивающие формирование
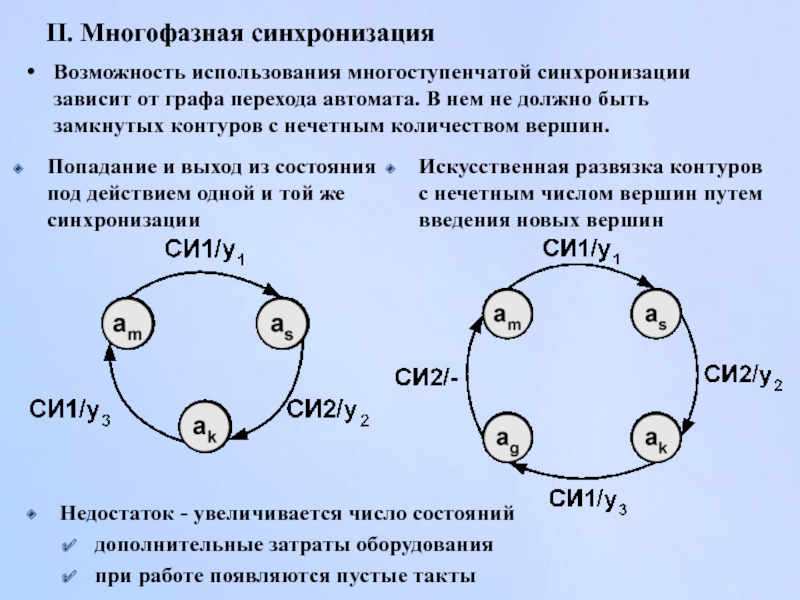
Слайд 75Возможность использования многоступенчатой синхронизации зависит от графа перехода автомата. В нем
II. Многофазная синхронизация
Попадание и выход из состояния под действием одной и той же синхронизации
Искусственная развязка контуров с нечетным числом вершин путем введения новых вершин
Недостаток - увеличивается число состояний
дополнительные затраты оборудования
при работе появляются пустые такты
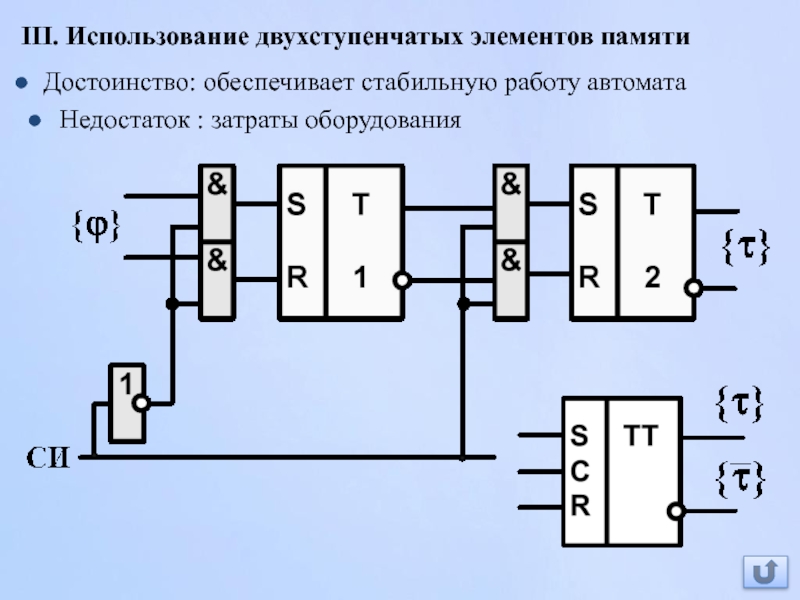
Слайд 76III. Использование двухступенчатых элементов памяти
Недостаток : затраты оборудования
Достоинство: обеспечивает стабильную
Слайд 77III. Использование двухступенчатых элементов памяти
Принцип действия основан на разделении во времени
Когда отсутствует СИ, вторая ступень закрыта и на выходе не изменяются сигналы, при этом через инвертор открывается
1-ая ступень и под действием не изменившихся функций возбуждения в 1-ой ступени формируется новое состояние (на выходе - старое)
По приходу СИ первая ступень закрывается, но открывается вторая и новое состояние переписывается из первой ступени во вторую. На выходе появляются новые сигналы состояний, по цепи обратной связи формируют новые функции возбуждения, но первая ступень все ещё закрыта и повторного переключения памяти не происходит
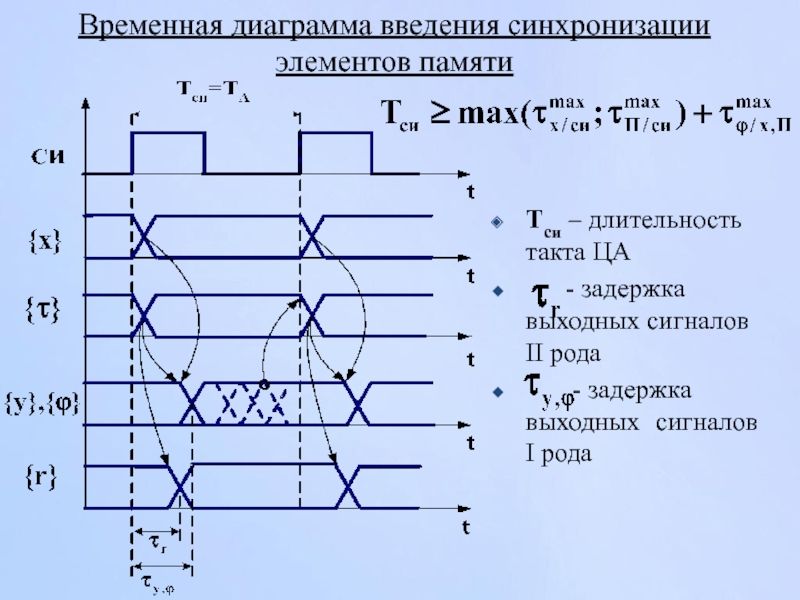
Слайд 78Временная диаграмма введения синхронизации элементов памяти
Тси – длительность такта ЦА
- задержка выходных сигналов I рода
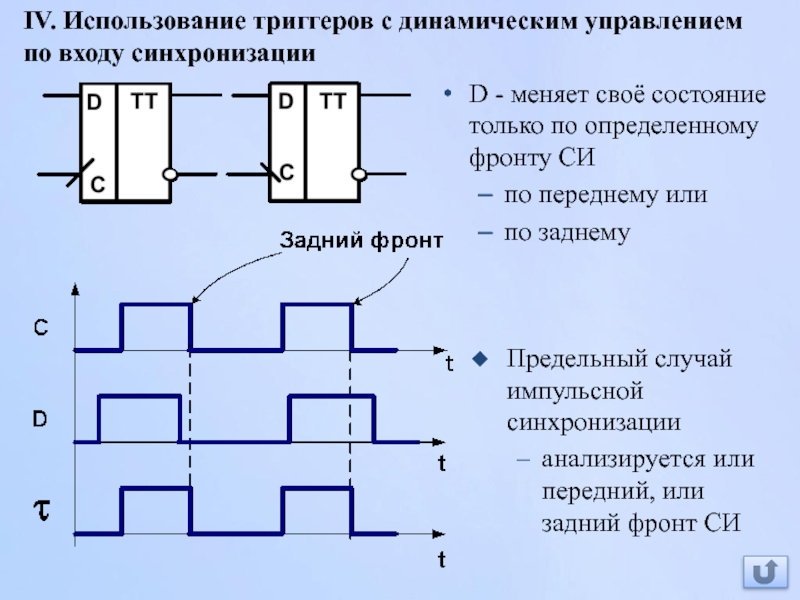
Слайд 79IV. Использование триггеров с динамическим управлением по входу синхронизации
D - меняет
по переднему или
по заднему
Предельный случай импульсной синхронизации
анализируется или передний, или задний фронт СИ
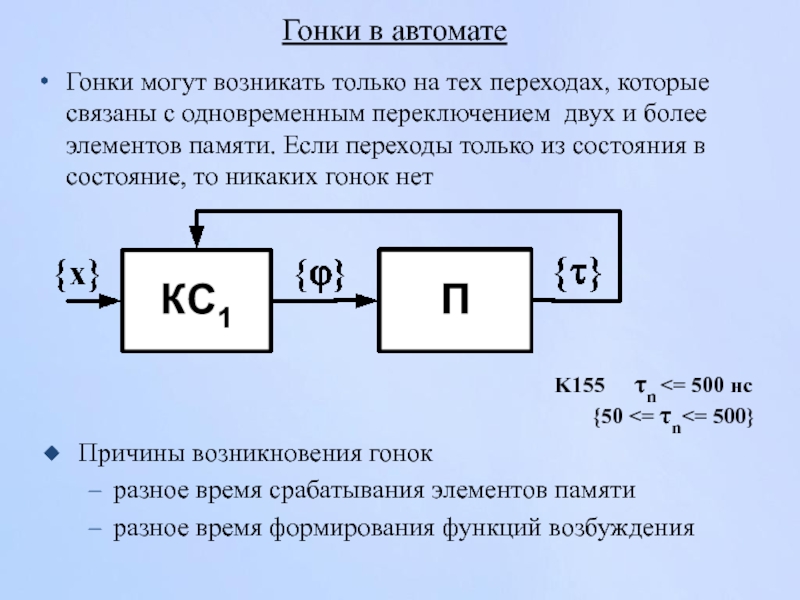
Слайд 80Гонки в автомате
Гонки могут возникать только на тех переходах, которые связаны
Причины возникновения гонок
разное время срабатывания элементов памяти
разное время формирования функций возбуждения
K155 τn <= 500 нс
{50 <= τn<= 500}
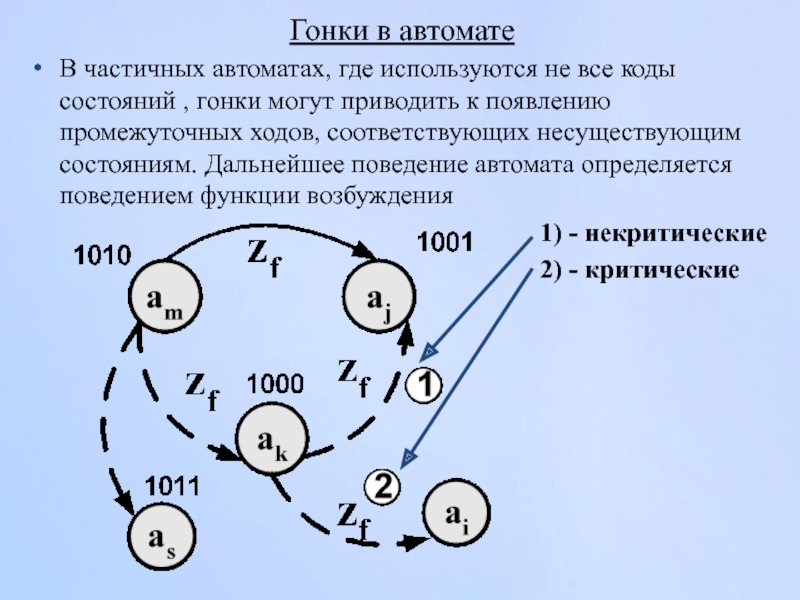
Слайд 81В частичных автоматах, где используются не все коды состояний , гонки
Гонки в автомате
1) - некритические
2) - критические
Слайд 82Способы устранения гонок
Аппаратные
импульсная синхронизация
использование двухступенчатых элементов памяти
использование триггеров с динамическим
Структурные – использование специальных методов кодирования состояния
соседнее кодирование
кодирование с учетом условий развязки пар переходов
Слайд 83Соседнее кодирование
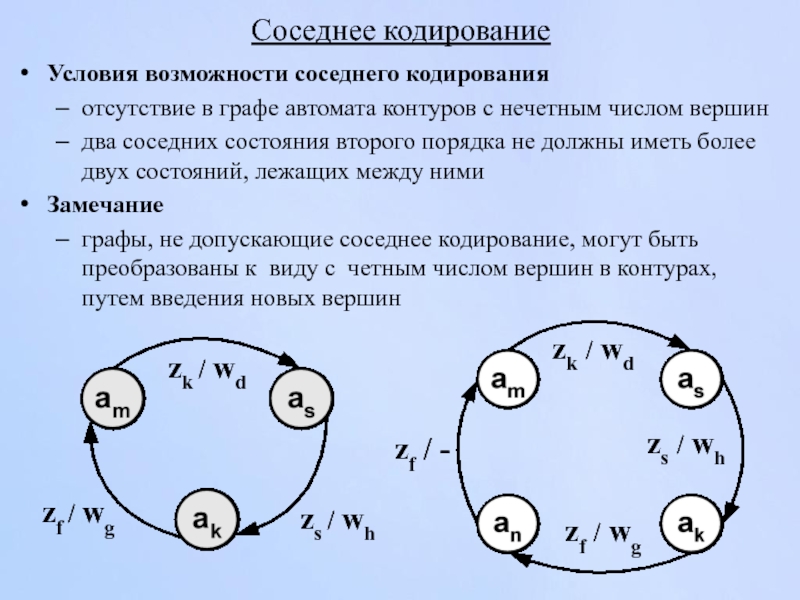
Условия возможности соседнего кодирования
отсутствие в графе автомата контуров с нечетным
два соседних состояния второго порядка не должны иметь более двух состояний, лежащих между ними
Замечание
графы, не допускающие соседнее кодирование, могут быть преобразованы к виду с четным числом вершин в контурах, путем введения новых вершин
zf / wg
zk / wd
zs / wh
zf / wg
zf / -
zk / wd
zs / wh
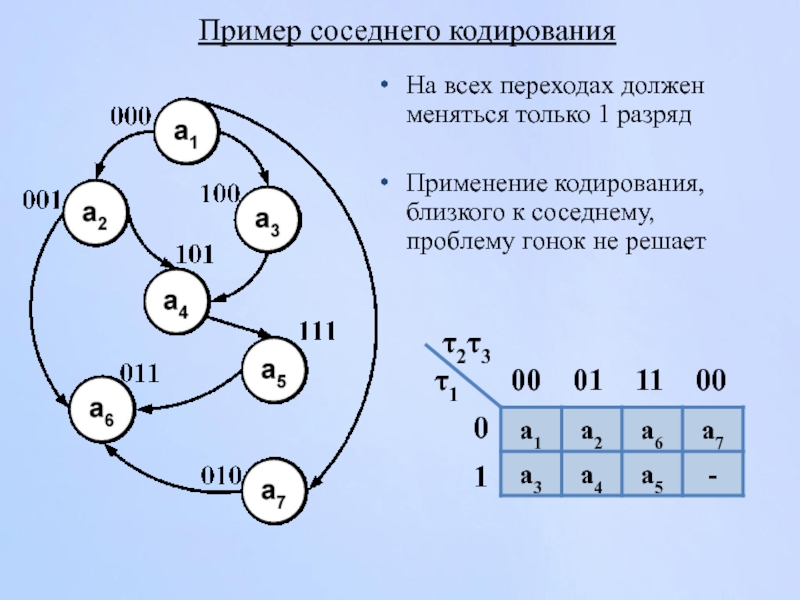
Слайд 84Пример соседнего кодирования
На всех переходах должен меняться только 1 разряд
Применение кодирования,
τ2τ3
τ1 00 01 11 00
0
1
Слайд 85Кодирование с учетом условий развязки пар переходов
Теорема
гонки в автомате отсутствуют, когда
пары кодов состояний называют развязанными, если какой-либо разряд кода принимает одно значение в первой паре и противоположное в другой
0010 1110
0111 1101
Методика
выявить все пары переходов, происходящих под действием одних входных сигналов
закодировать состояния взаимно развязанными парами кодов
Слайд 86Операционные устройства
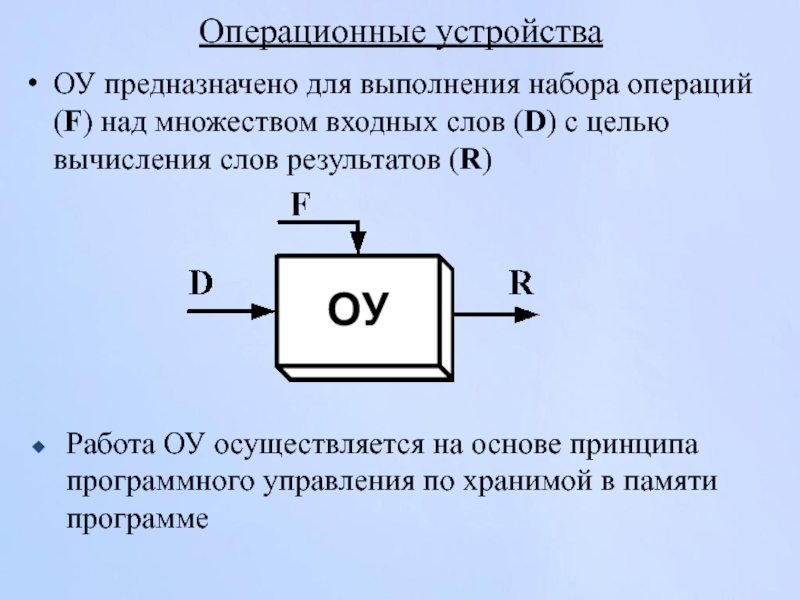
ОУ предназначено для выполнения набора операций (F) над множеством входных
Работа ОУ осуществляется на основе принципа программного управления по хранимой в памяти программе
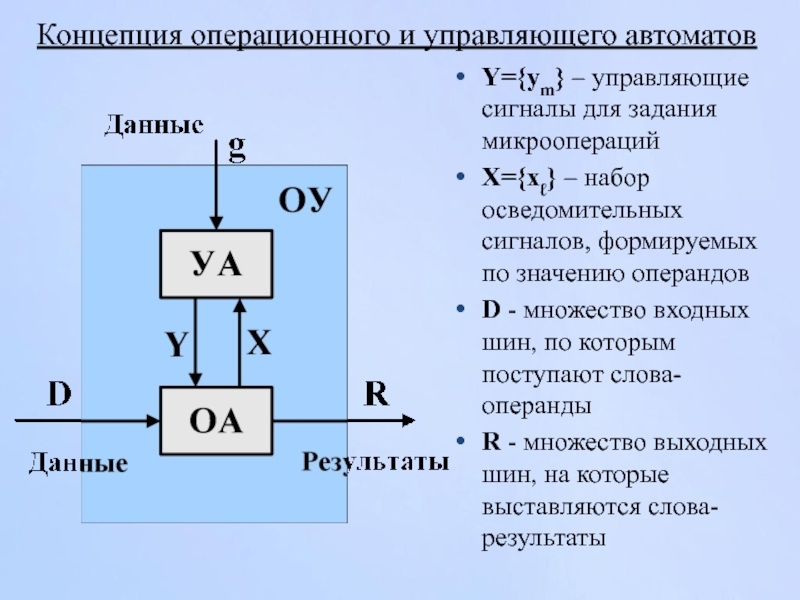
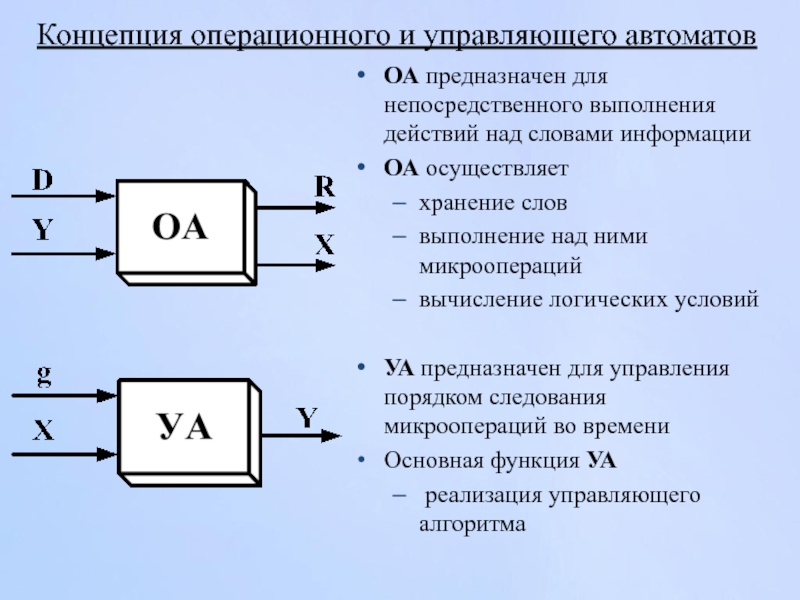
Слайд 87Концепция операционного и управляющего автоматов
Y={ym} – управляющие сигналы для задания микроопераций
X={xℓ}
D - множество входных шин, по которым поступают слова-операнды
R - множество выходных шин, на которые выставляются слова-результаты
Слайд 88Концепция операционного и управляющего автоматов
ОА предназначен для непосредственного выполнения действий над
ОА осуществляет
хранение слов
выполнение над ними микроопераций
вычисление логических условий
УА предназначен для управления порядком следования микроопераций во времени
Основная функция УА
реализация управляющего алгоритма
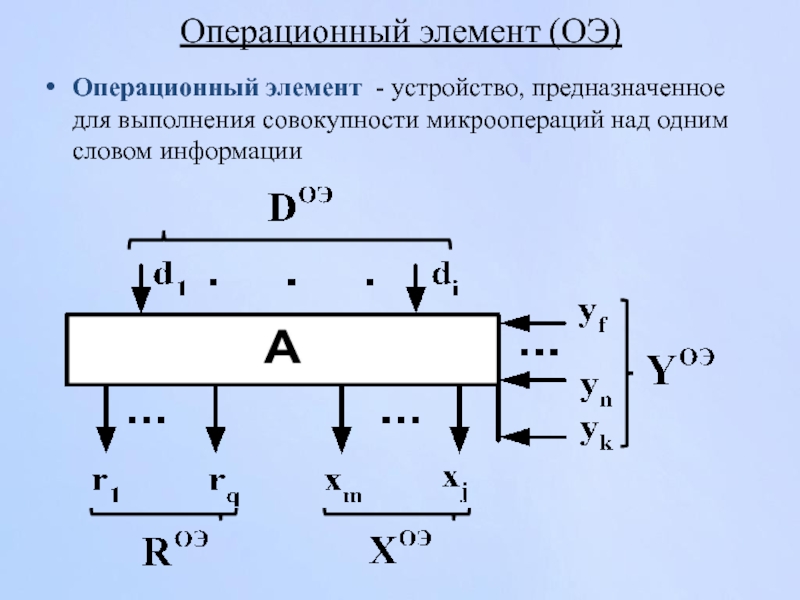
Слайд 89Операционный элемент (ОЭ)
Операционный элемент - устройство, предназначенное для выполнения совокупности микроопераций
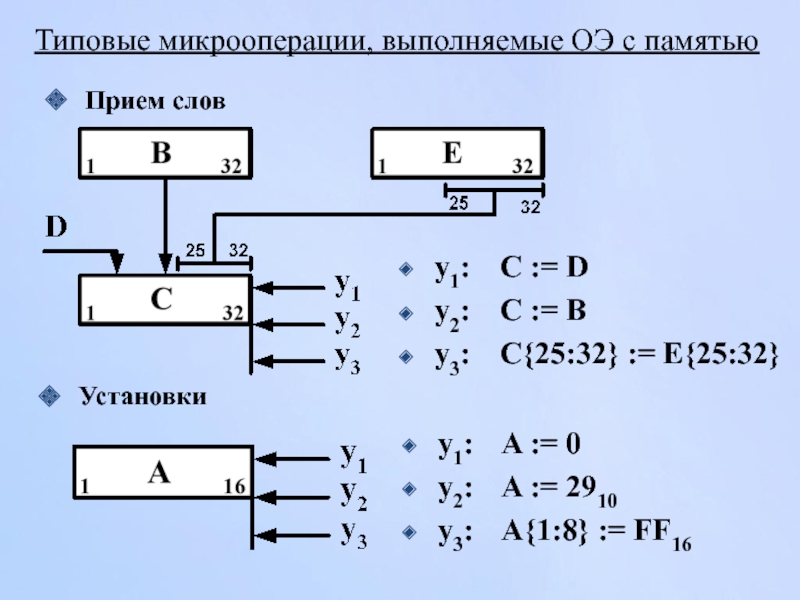
Слайд 91Типовые микрооперации, выполняемые ОЭ с памятью
Прием слов
y1: C := D
y2: C
y3: C{25:32} := E{25:32}
Установки
y1: A := 0
y2: A := 2910
y3: A{1:8} := FF16
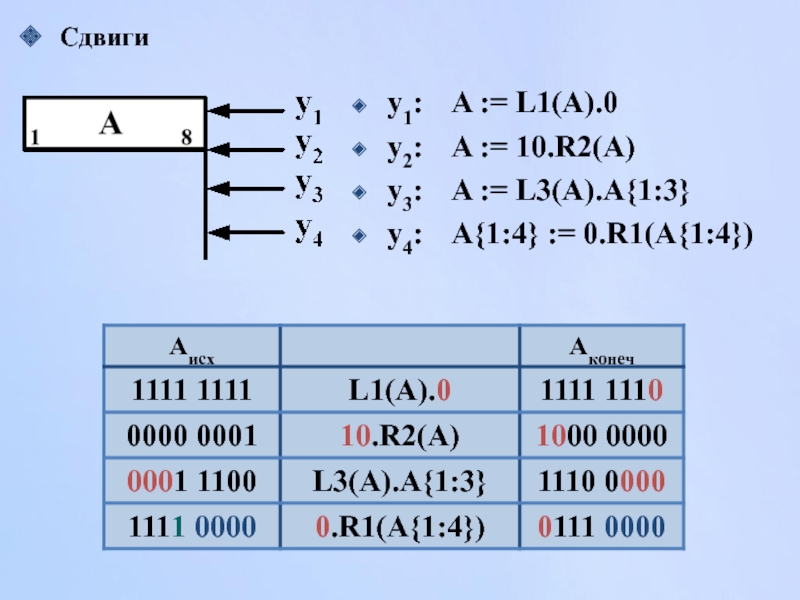
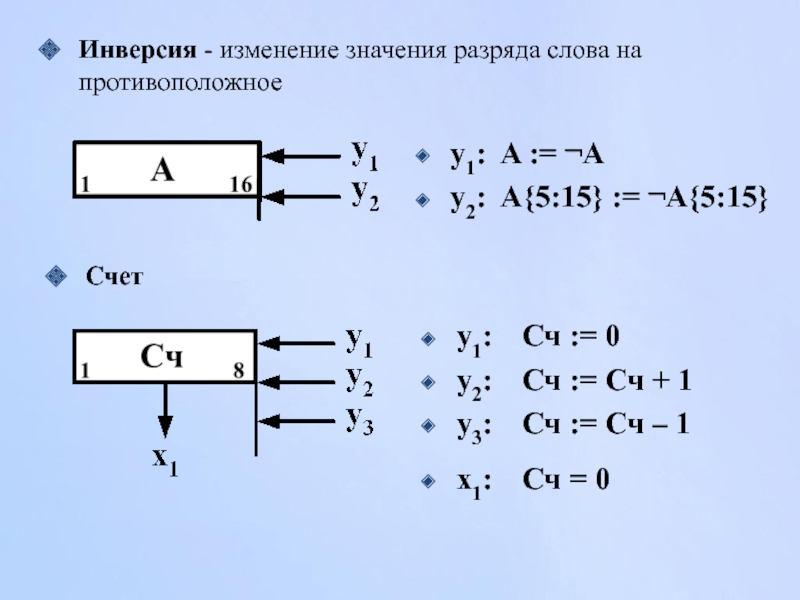
Слайд 93Инверсия - изменение значения разряда слова на противоположное
y1: A := ¬A
y2: A{5:15} :=
Счет
y1: Сч := 0
y2: Сч := Сч + 1
y3: Сч := Сч – 1
x1: Сч = 0
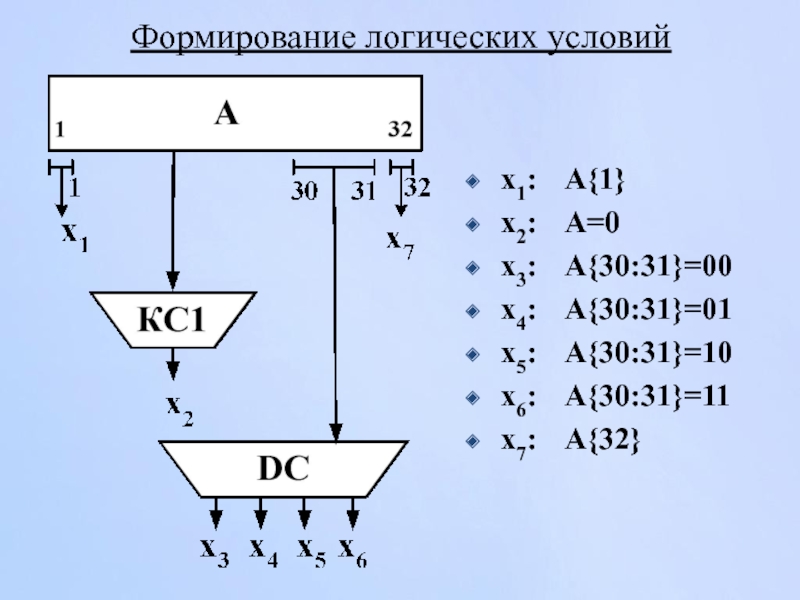
Слайд 94Формирование логических условий
x1: A{1}
x2: A=0
x3: A{30:31}=00
x4: A{30:31}=01
x5: A{30:31}=10
x6: A{30:31}=11
x7: A{32}
Слайд 99Использование закодированных микропрограмм
Используют при минимизации микропрограмм
Используют для объединения отдельных микропрограмм
При синтезе
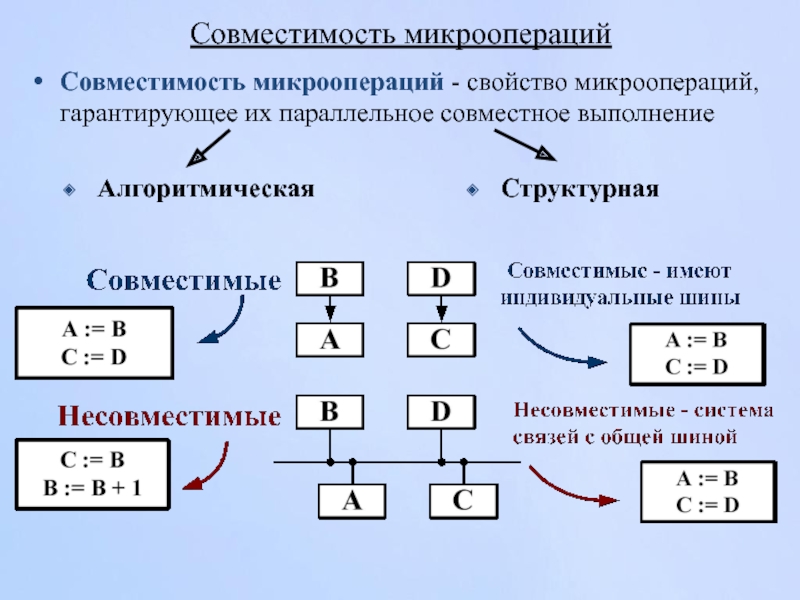
Слайд 100Совместимость микроопераций
Совместимость микроопераций - свойство микроопераций, гарантирующее их параллельное совместное выполнение
Алгоритмическая
Структурная
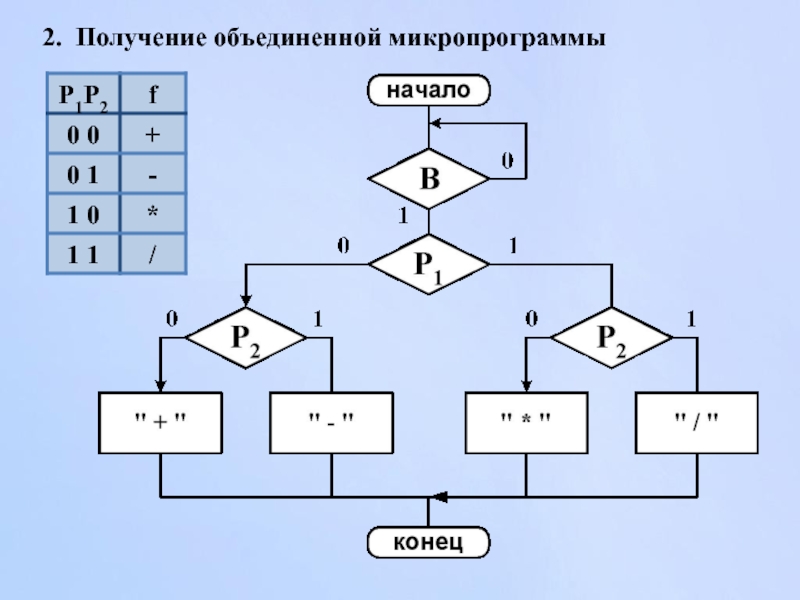
Слайд 101Объединение и минимизация микропрограмм
Цель
получение минимальной с точки зрения затрат оборудования микропрограммы
Для
кодирование операций
получение объединенной микропрограммы
минимизация микропрограммы
1. Кодирование
P2
P1 0 1
0
1
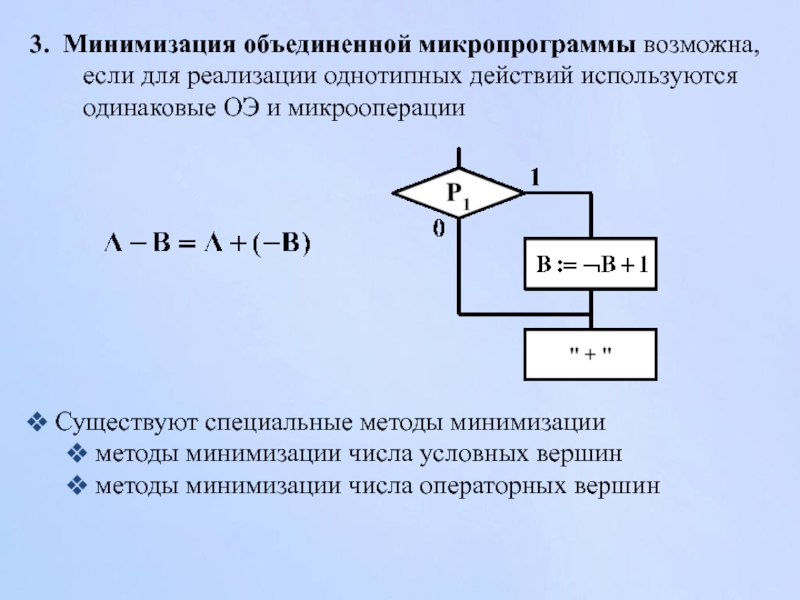
Слайд 1033. Минимизация объединенной микропрограммы возможна, если для реализации однотипных действий используются
Существуют специальные методы минимизации
методы минимизации числа условных вершин
методы минимизации числа операторных вершин
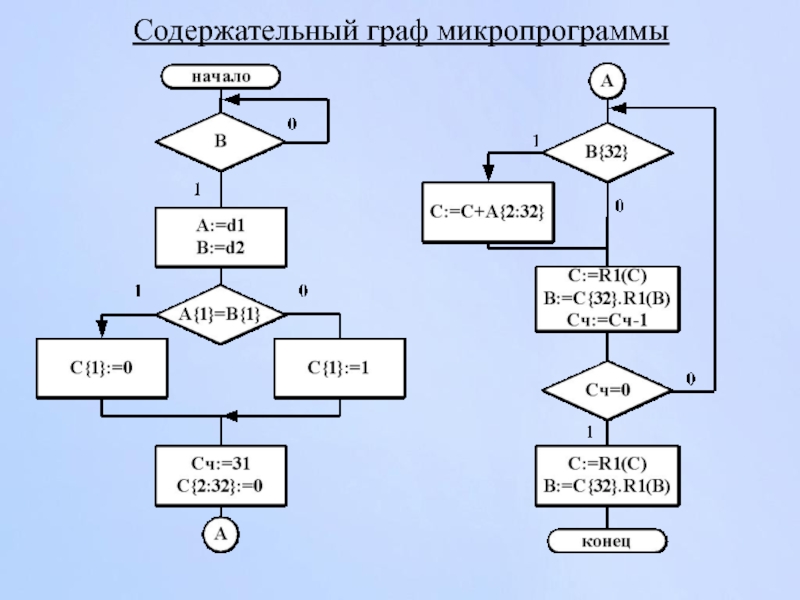
Слайд 104Интерпретация микропрограммы автоматом Мили
Отметка закодированного графа микропрограммы (ГМП) - получение множества
Порядок отметки
1. a1 - отметка входа в вершину, следующую за начальной, и входа конечной вершины
2. Входы всех вершин, следующих за операторными отмечаются: a2, a3,…
3. Вход вершины может быть отмечен только одним символом
4. Входы различных вершин, за исключением конечной, отмечаются различными символами
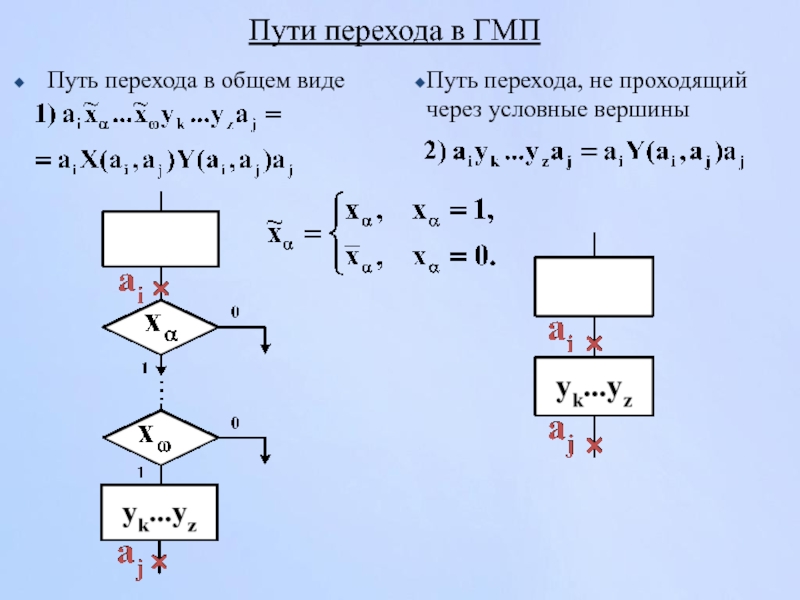
Слайд 108Пути перехода в ГМП
Путь перехода в общем виде
Путь перехода, не проходящий
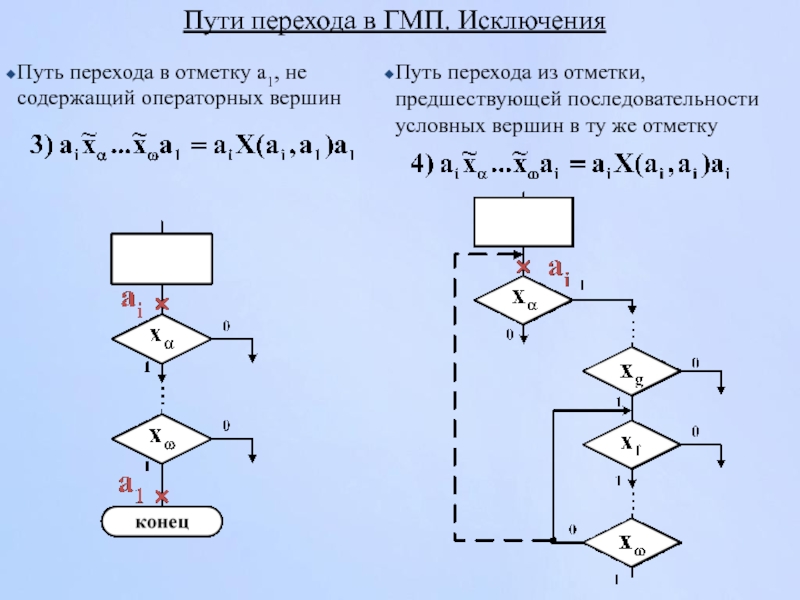
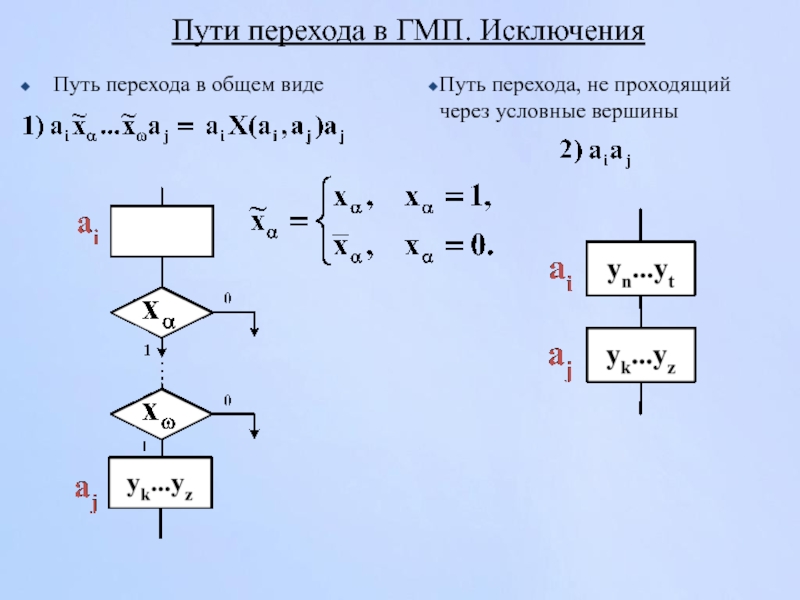
Слайд 109Пути перехода в ГМП. Исключения
Путь перехода из отметки, предшествующей последовательности условных
Путь перехода в отметку а1, не содержащий операторных вершин
Слайд 112Корректность интерпретации микропрограммы автоматом Мили
Корректная интерпретация микропрограммы автоматом Мили возможна при
Если на некотором переходе есть функциональная зависимость
выполнение микрокоманды функционального оператора Y(aiaj) может привести к изменению логического условия xρ
Проверить корректность интерпретации микропрограммы автоматом Мили можно путем анализа распределения сдвигов, определяющего для каждого функционального оператора Y(aiaj) подмножество осведомительных сигналов, которые могут меняться при его выполнении
Слайд 115Пути перехода в ГМП. Исключения
Путь перехода в общем виде
Путь перехода, не
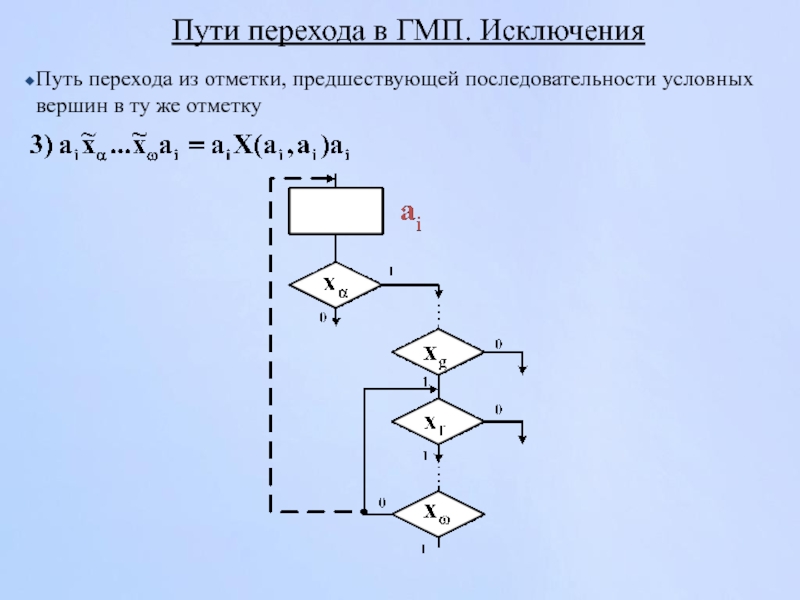
Слайд 116Пути перехода в ГМП. Исключения
Путь перехода из отметки, предшествующей последовательности условных
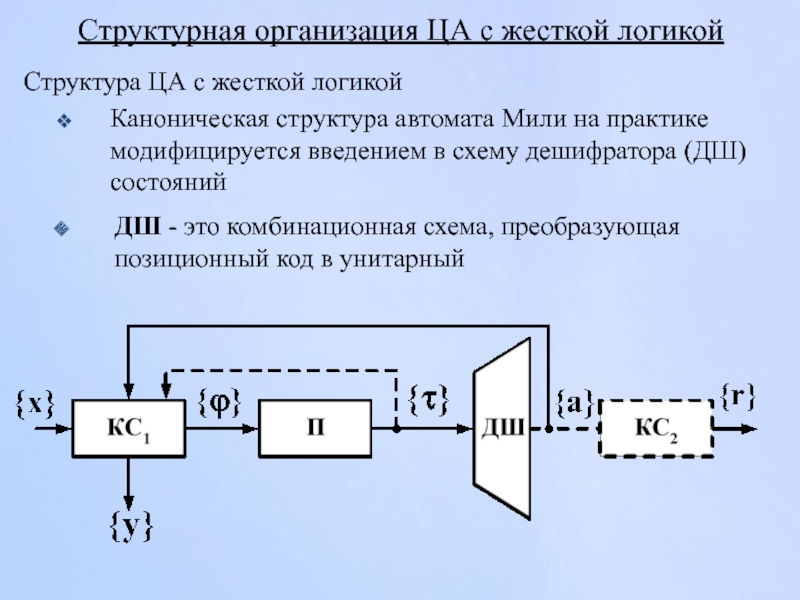
Слайд 119Структурная организация ЦА с жесткой логикой
Структура ЦА с жесткой логикой
Каноническая структура
ДШ - это комбинационная схема, преобразующая позиционный код в унитарный
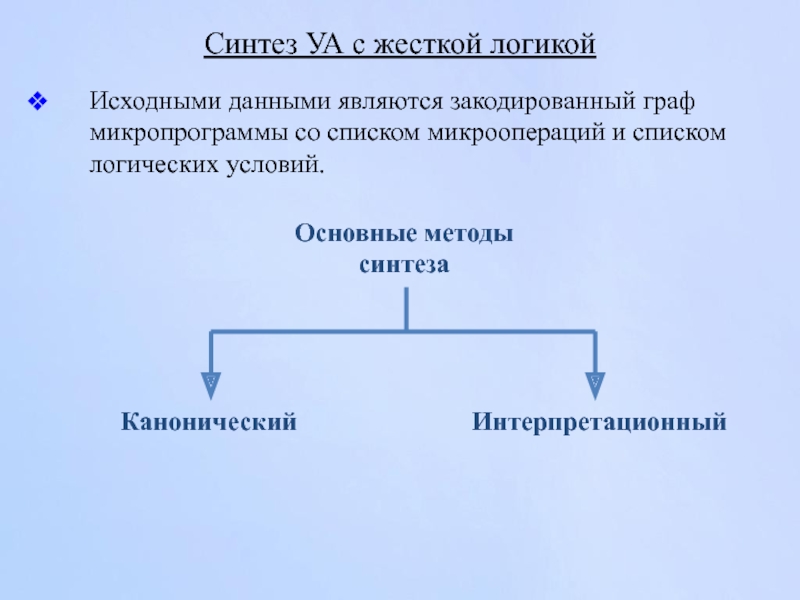
Слайд 120Синтез УА с жесткой логикой
Исходными данными являются закодированный граф микропрограммы со
Основные методы синтеза
Канонический
Интерпретационный
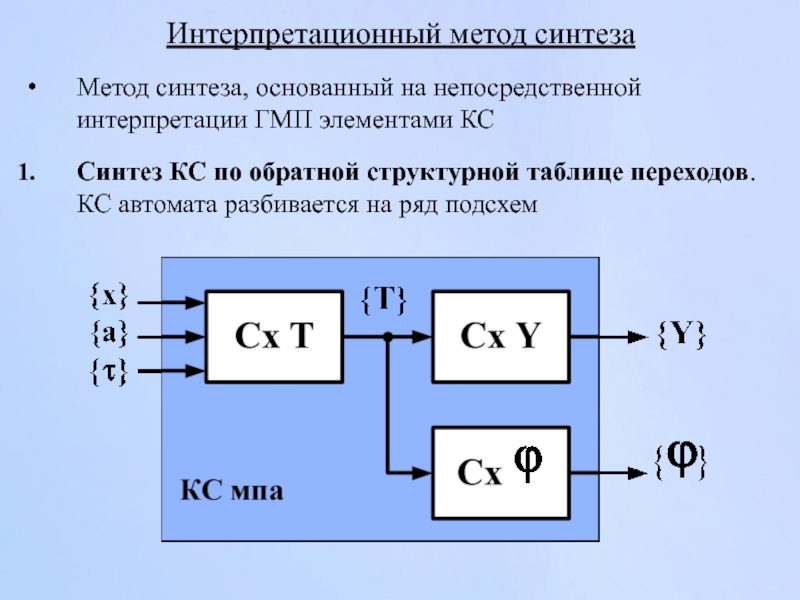
Слайд 121Интерпретационный метод синтеза
Метод синтеза, основанный на непосредственной интерпретации ГМП элементами КС
Синтез
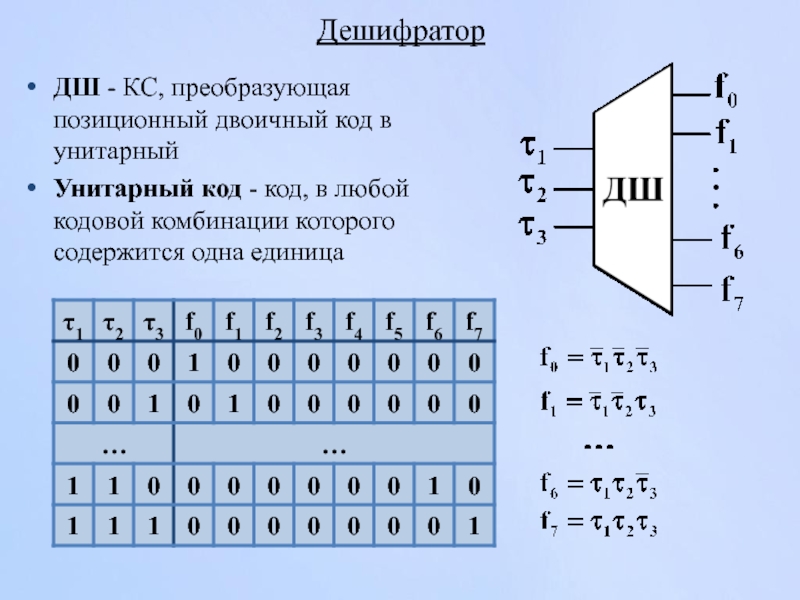
Слайд 123Дешифратор
ДШ - КС, преобразующая позиционный двоичный код в унитарный
Унитарный код -
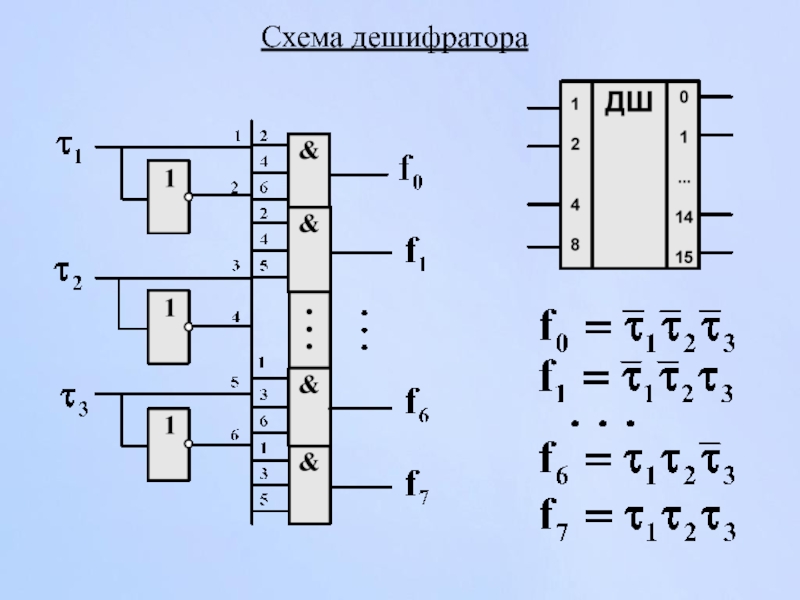
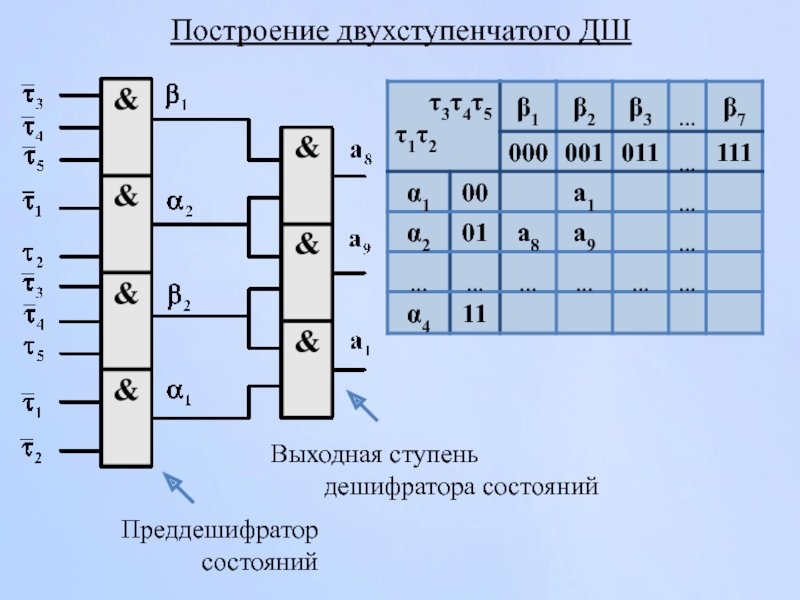
Слайд 126Построение двухступенчатого ДШ
Преддешифратор состояний
Выходная ступень дешифратора состояний
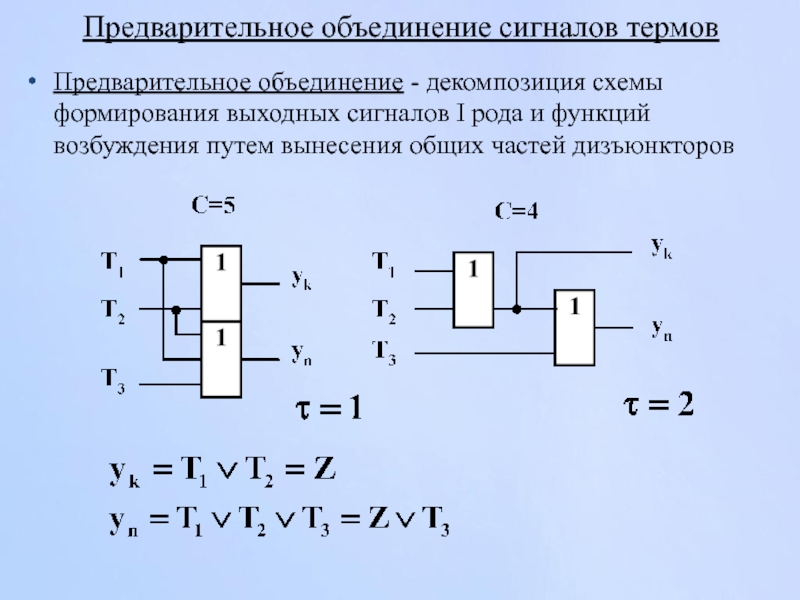
Слайд 127Предварительное объединение сигналов термов
Предварительное объединение - декомпозиция схемы формирования выходных сигналов
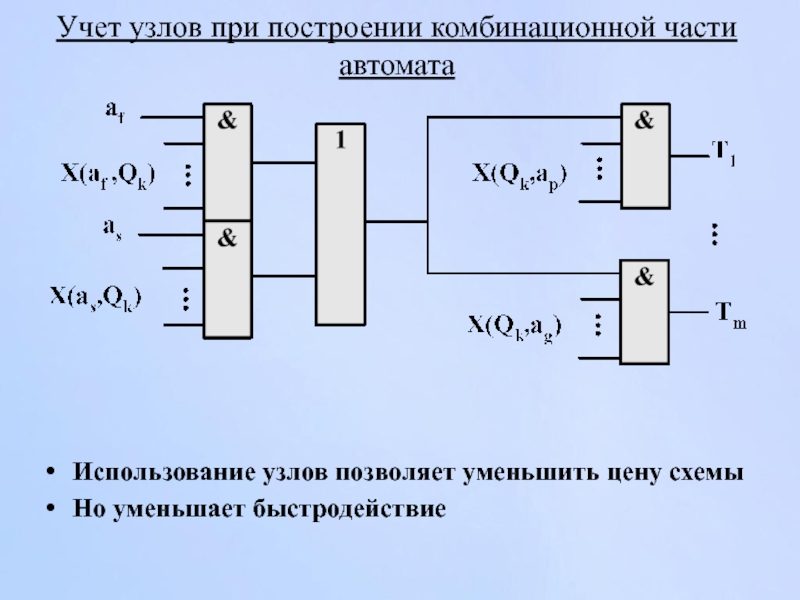
Слайд 134Учет узлов при построении комбинационной части автомата
Использование узлов позволяет уменьшить цену
Но уменьшает быстродействие
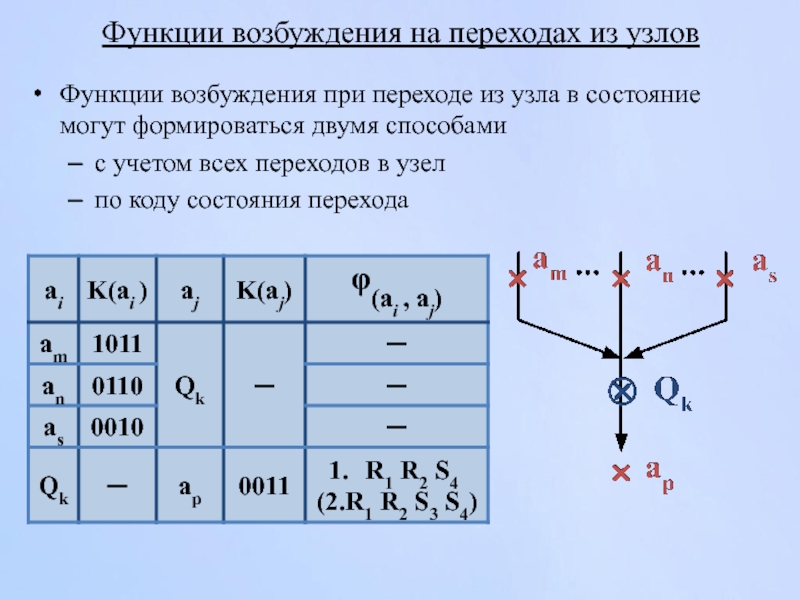
Слайд 135Функции возбуждения на переходах из узлов
Функции возбуждения при переходе из узла
с учетом всех переходов в узел
по коду состояния перехода
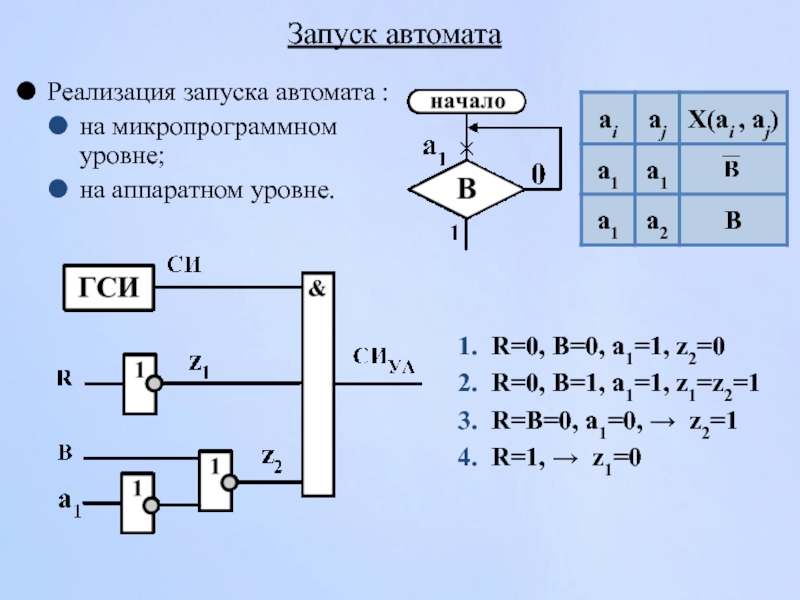
Слайд 137Запуск автомата
Реализация запуска автомата :
на микропрограммном уровне;
на аппаратном уровне.
1. R=0, B=0,
2. R=0, B=1, a1=1, z1=z2=1
3. R=B=0, a1=0, → z2=1
4. R=1, → z1=0
Слайд 146ПЛУ с матричной структурой
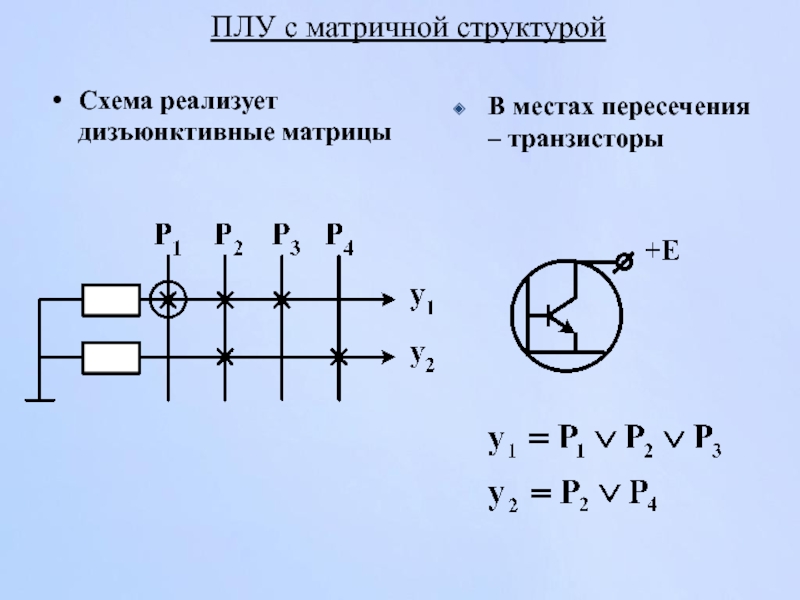
В местах пересечения – диоды
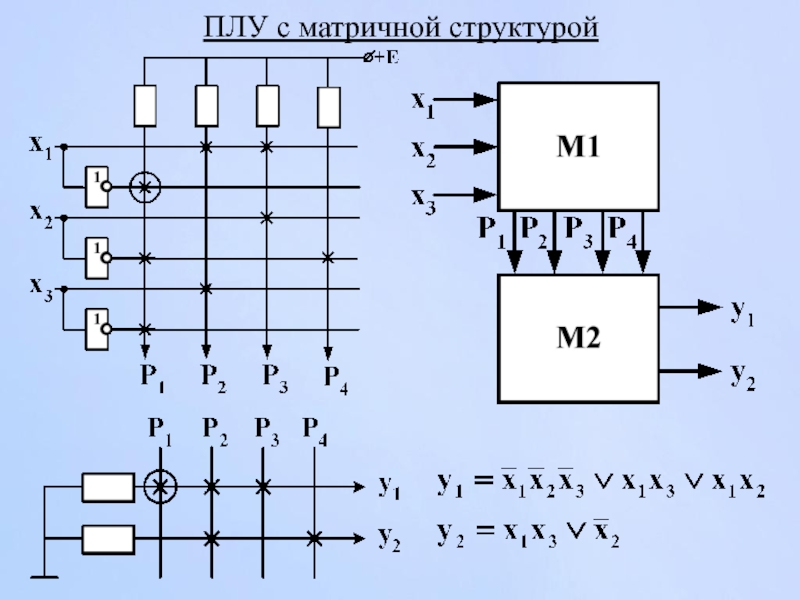
Схема реализует конъюнктивные матрицы
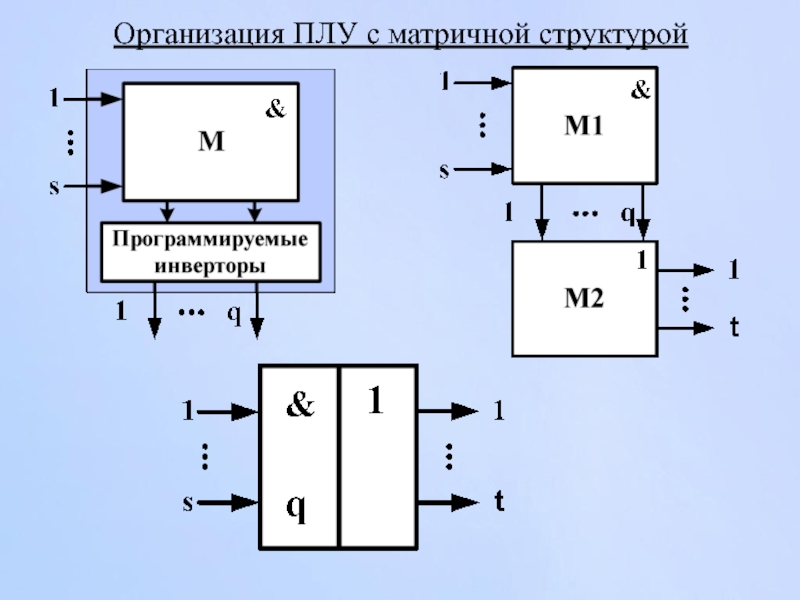
Слайд 147Схема реализует дизъюнктивные матрицы
ПЛУ с матричной структурой
В местах пересечения – транзисторы
Слайд 153Синтез УА на ПЛМ
I. Одноуровневая тривиальная реализация на 1 ПЛМ
одновходовые
двухвходовые триггеры
Слайд 155II. Одноуровневая тривиальная реализация на нескольких ПЛМ
1) Собственно одноуровневая
Система уравнений
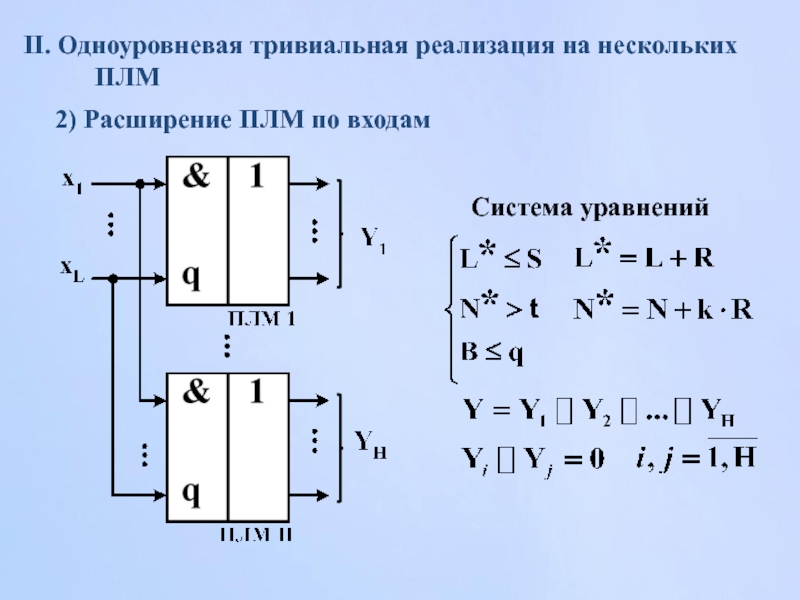
Слайд 156II. Одноуровневая тривиальная реализация на нескольких ПЛМ
2) Расширение ПЛМ по входам
Система
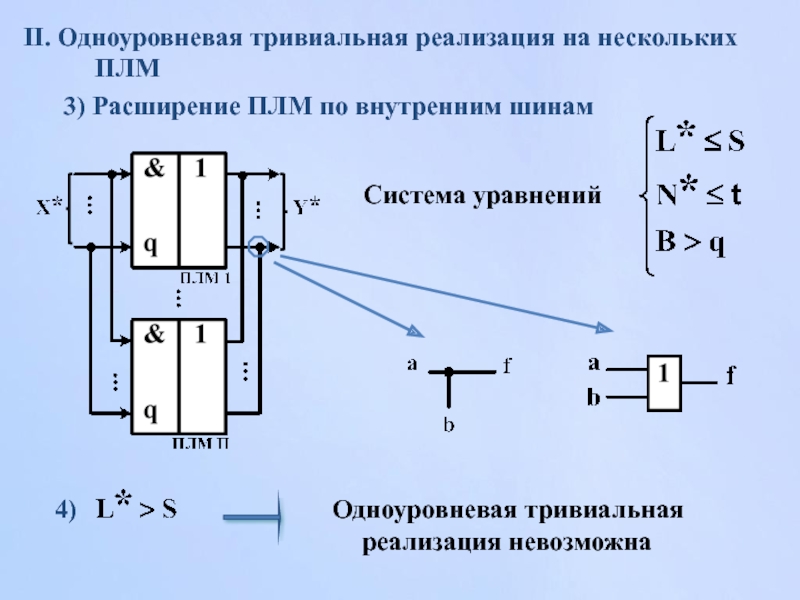
Слайд 157II. Одноуровневая тривиальная реализация на нескольких ПЛМ
3) Расширение
Система уравнений
Одноуровневая тривиальная реализация невозможна
4)
Слайд 158Функции на выходе зависят не от всех входных переменных
III. Одноуровневая нетривиальная
Слайд 159Пример одноуровневой нетривиальной реализации
ПЛМ (3, 2, 4)
Задачи, решаемые при реализации
Преобразование
Распределение уравнений по различным ПЛМ таким образом, чтобы для каждой ПЛМ выполнялось условие Li ≤ Lmax (≤ s)
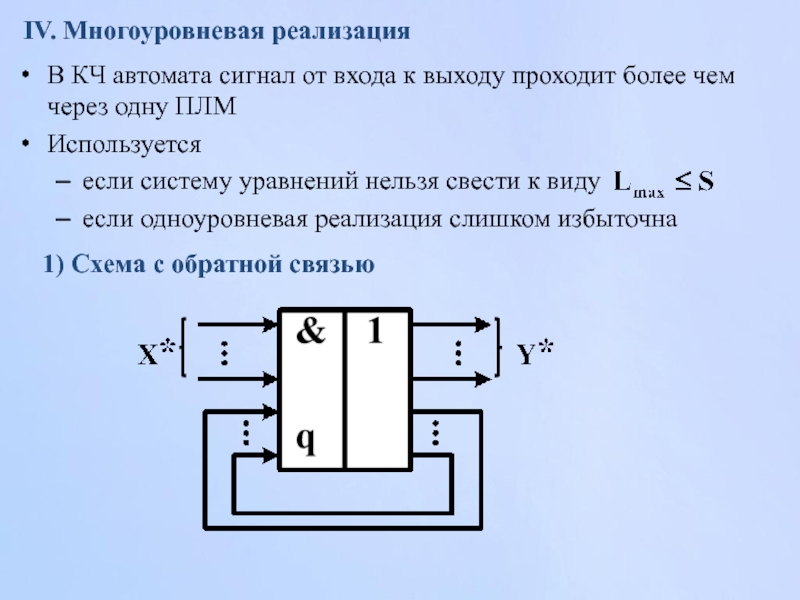
Слайд 160В КЧ автомата сигнал от входа к выходу проходит более чем
Используется
если систему уравнений нельзя свести к виду
если одноуровневая реализация слишком избыточна
IV. Многоуровневая реализация
1) Схема с обратной связью
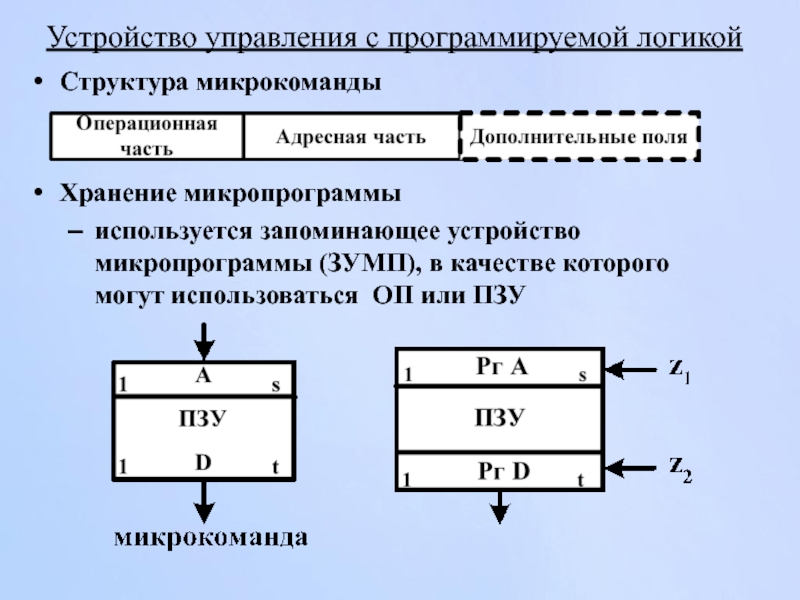
Слайд 162Устройство управления с программируемой логикой
Структура микрокоманды
Хранение микропрограммы
используется запоминающее устройство микропрограммы (ЗУМП),
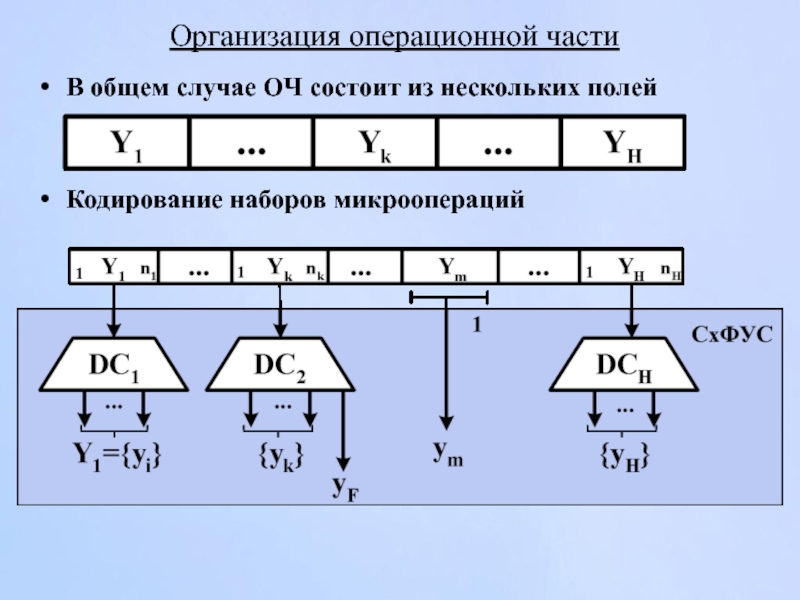
Слайд 164Организация операционной части
В общем случае ОЧ состоит из нескольких полей
Кодирование наборов
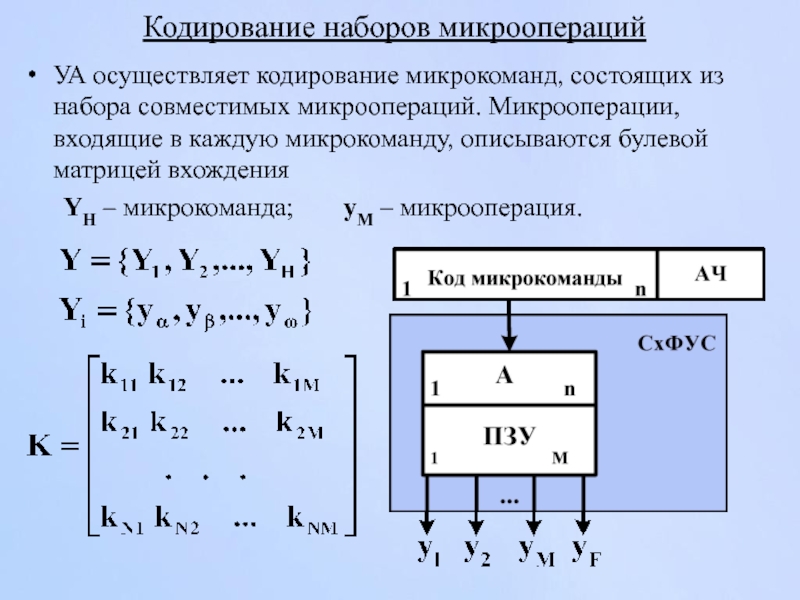
Слайд 165Кодирование наборов микроопераций
УА осуществляет кодирование микрокоманд, состоящих из набора совместимых микроопераций.
YH – микрокоманда; yM – микрооперация.
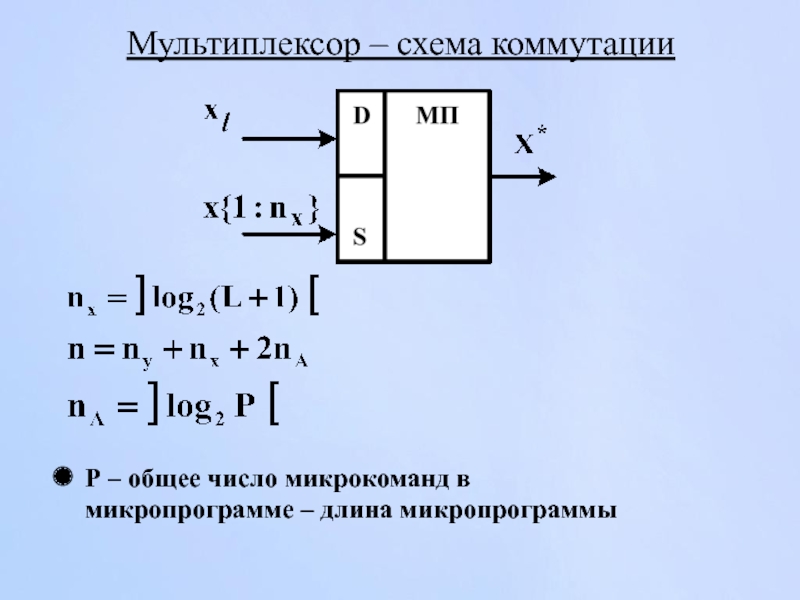
Слайд 168Мультиплексор – схема коммутации
Р – общее число микрокоманд в микропрограмме –
Слайд 169Пример разработки микропрограммы
Распределение микроопераций по совместно-кодированным полям
Слайд 170Пример разработки микропрограммы
Микропрограмма
Структура микрокоманды
Операционная часть
Адресная часть
Исходные данные
Слайд 172Принудительная адресация с одним адресом
Микропрограмма
Операционная часть
Адресная часть
Структура микрокоманды
Исходные данные
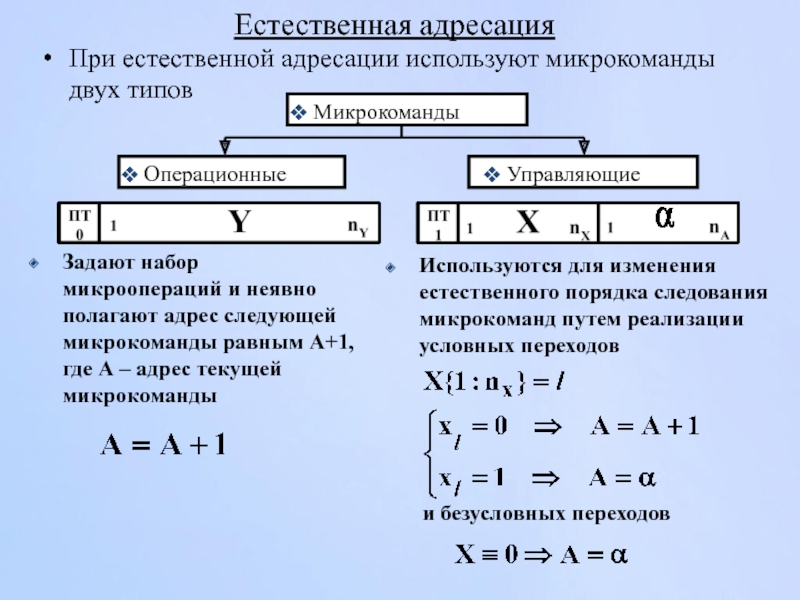
Слайд 173Используются для изменения естественного порядка следования микрокоманд путем реализации условных переходов
Естественная адресация
При естественной адресации используют микрокоманды двух типов
Микрокоманды
Операционные
Управляющие
Задают набор микроопераций и неявно полагают адрес следующей микрокоманды равным А+1, где А – адрес текущей микрокоманды