- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория автоматического управления в картинках презентация
Содержание
- 1. Теория автоматического управления в картинках
- 2. Содержание Что такое ТАУ Классификация сущностей ТАУ
- 3. О чем это ТАУ = наука преобразовании
- 4. Как у них Control theory = "матан" Process control – как это реализовать и применить
- 5. Гимн черному ящику =) Стандартная нотация (у
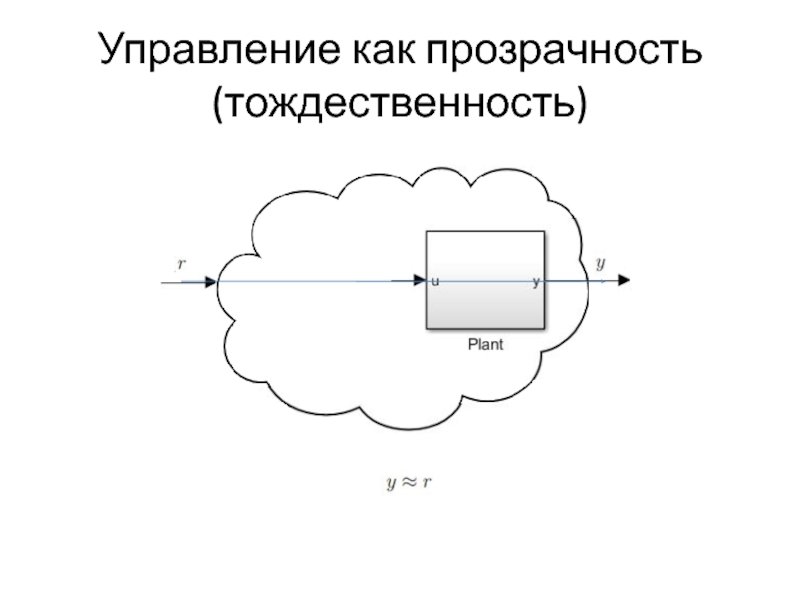
- 6. Управление как прозрачность (тождественность)
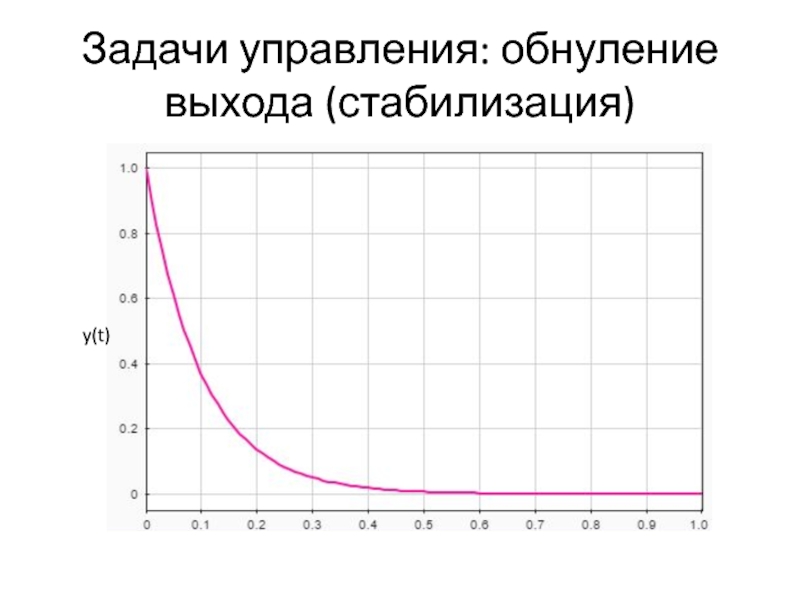
- 7. Задачи управления: обнуление выхода (стабилизация) y(t)
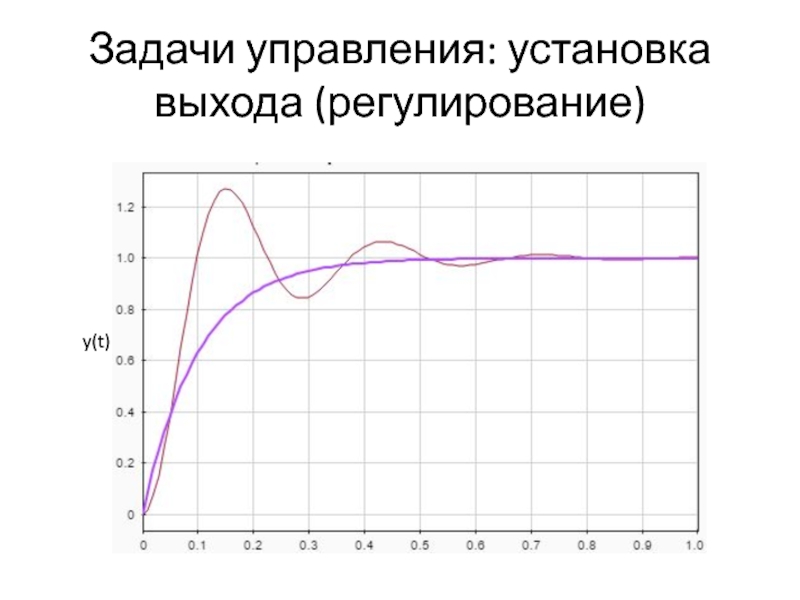
- 8. Задачи управления: установка выхода (регулирование) y(t)
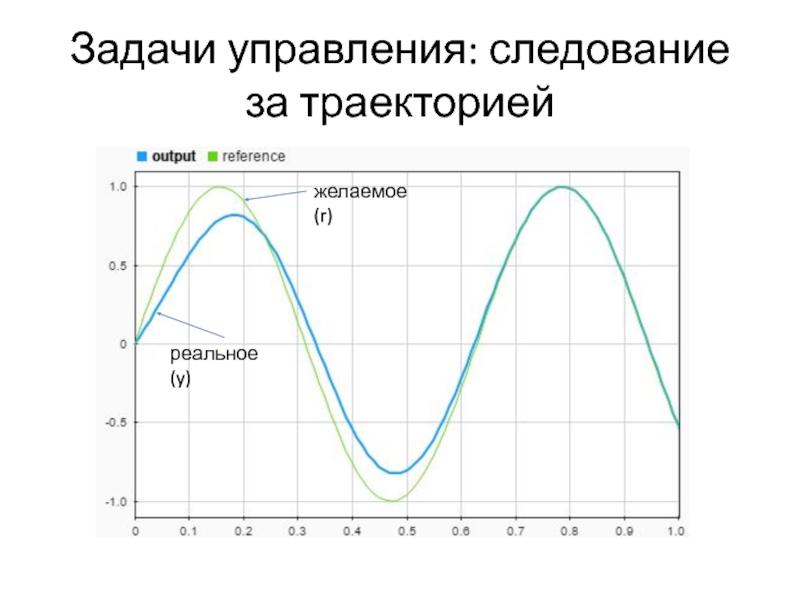
- 9. Задачи управления: следование за траекторией желаемое (r) реальное (y)
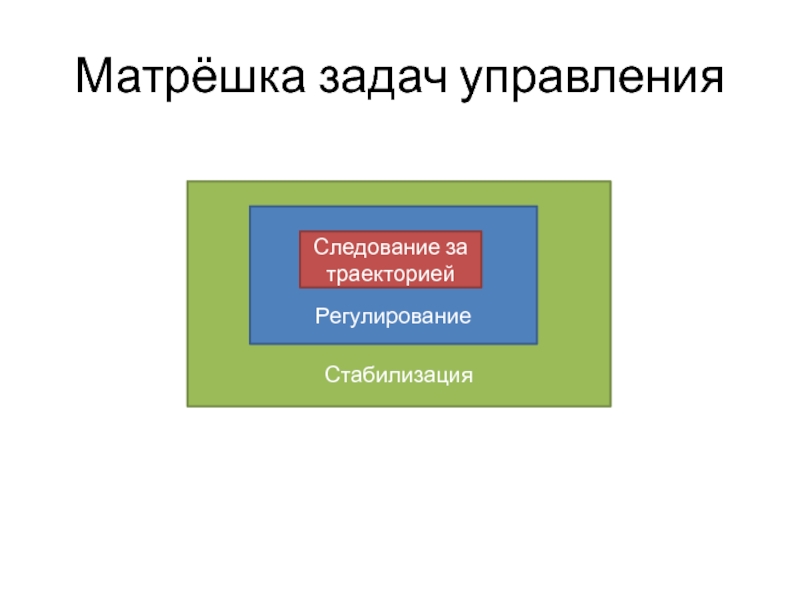
- 10. Стабилизация
- 11. Поведение: устойчивое и не устойчивое Реакция двух
- 12. Отклик: динамический и статический Вход (постоянный сигнал)
- 13. Количество входов: одномерные и многомерные системы SISO
- 14. Линейные и нелинейные системы Линейная система Нелинейная
- 15. Разомкнутое управление Проблемы: Моделирование: мы никогда не
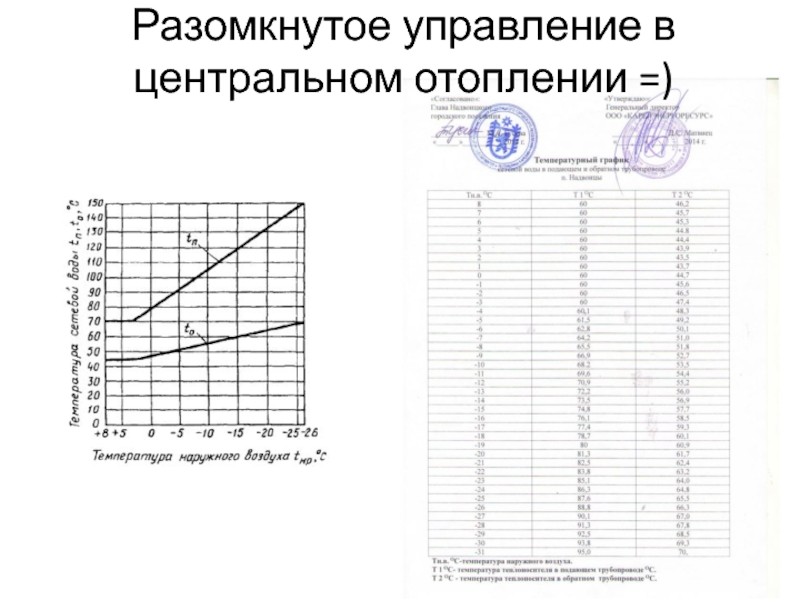
- 16. Разомкнутое управление в центральном отоплении =)
- 17. Замкнутое управление Это уже не обязательно инверсия
- 18. Релейный регулятор Если сигнал ошибки > предел,
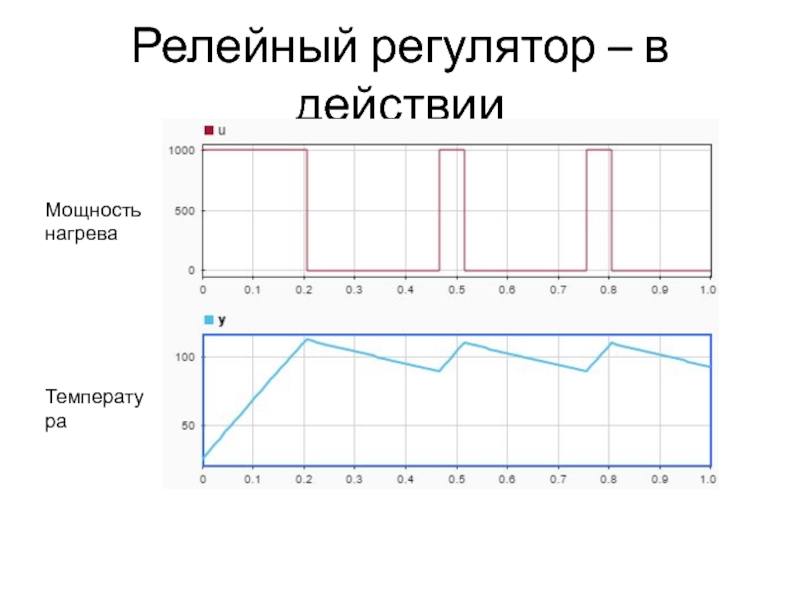
- 19. Релейный регулятор – в действии Температура Мощность нагрева
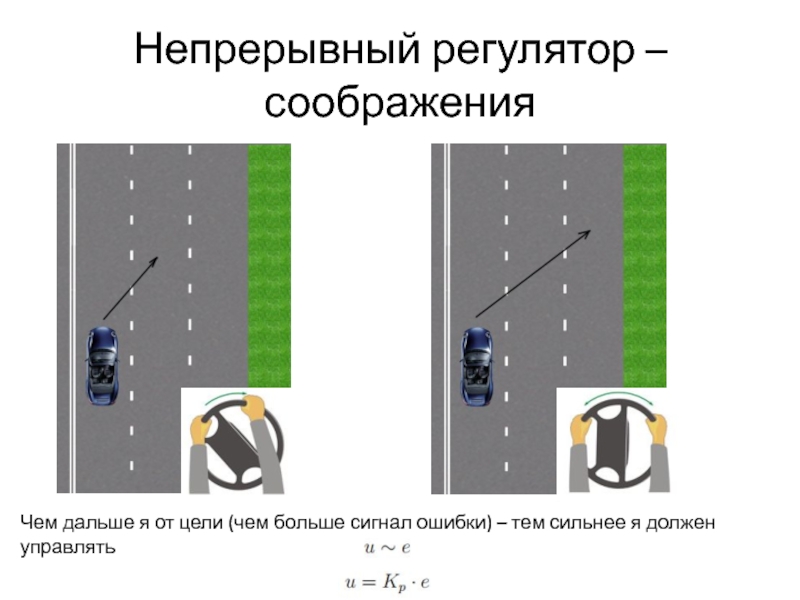
- 20. Непрерывный регулятор – соображения Чем дальше я
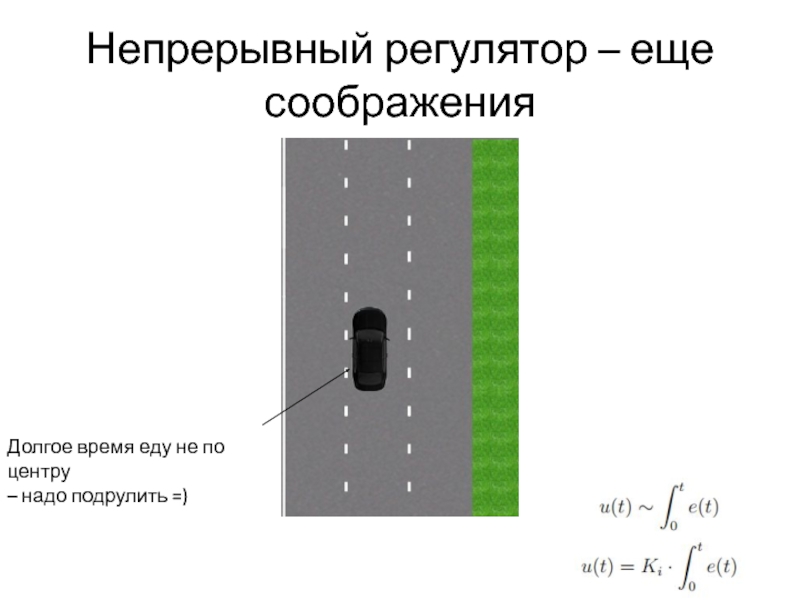
- 21. Непрерывный регулятор – еще соображения Долгое время
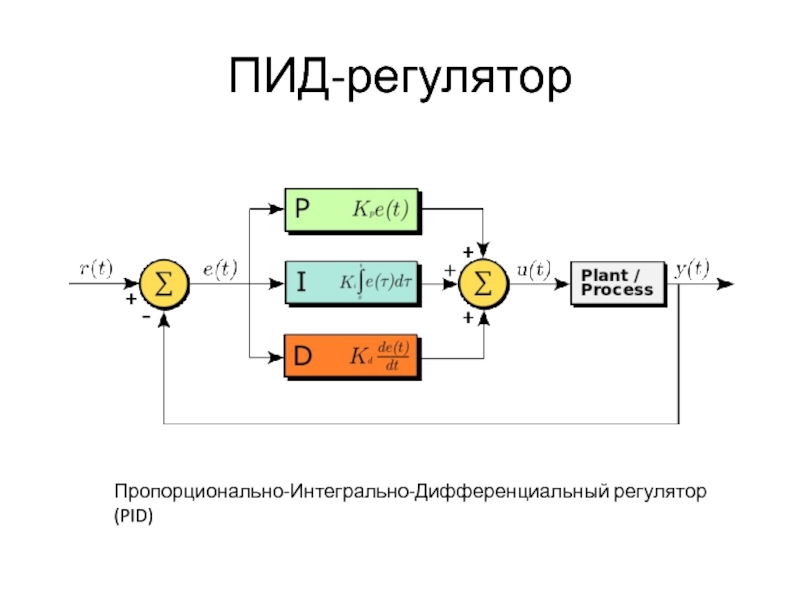
- 22. ПИД-регулятор Пропорционально-Интегрально-Дифференциальный регулятор (PID)
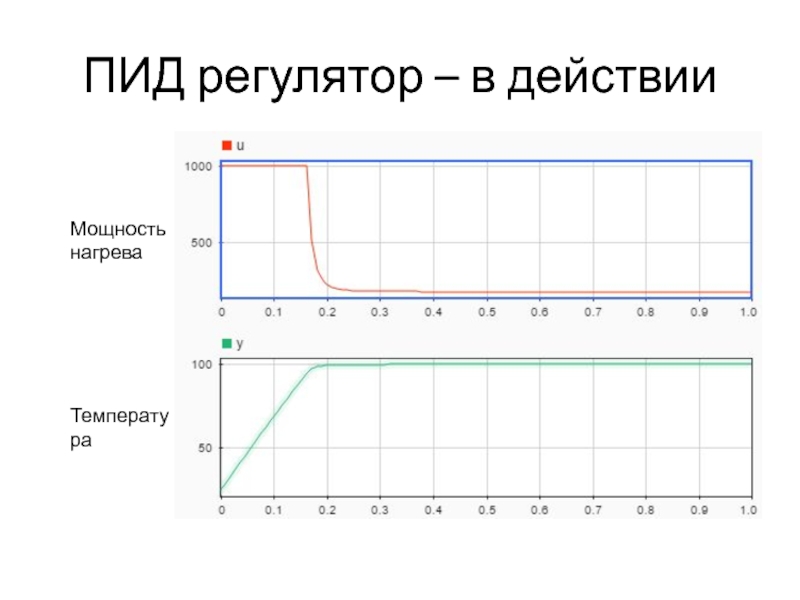
- 23. ПИД регулятор – в действии Температура Мощность нагрева
- 24. Алгоритм применения и настройки ПИД-регулятора Убедиться, что
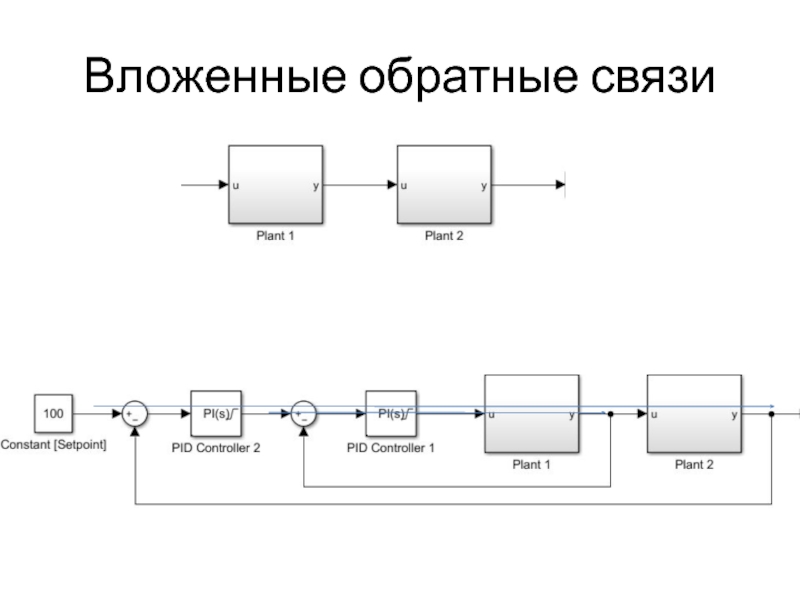
- 25. Вложенные обратные связи
- 26. Что делать с нелинейностями? Ничего не делать
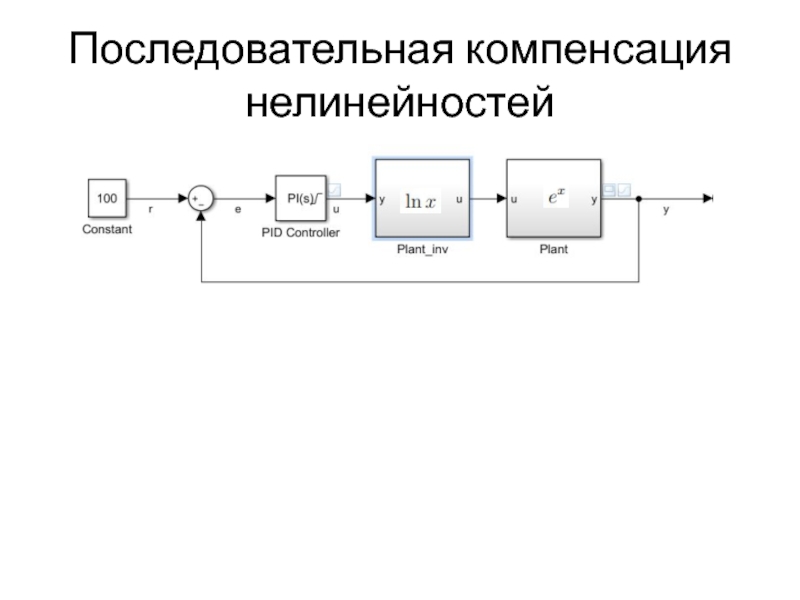
- 27. Последовательная компенсация нелинейностей
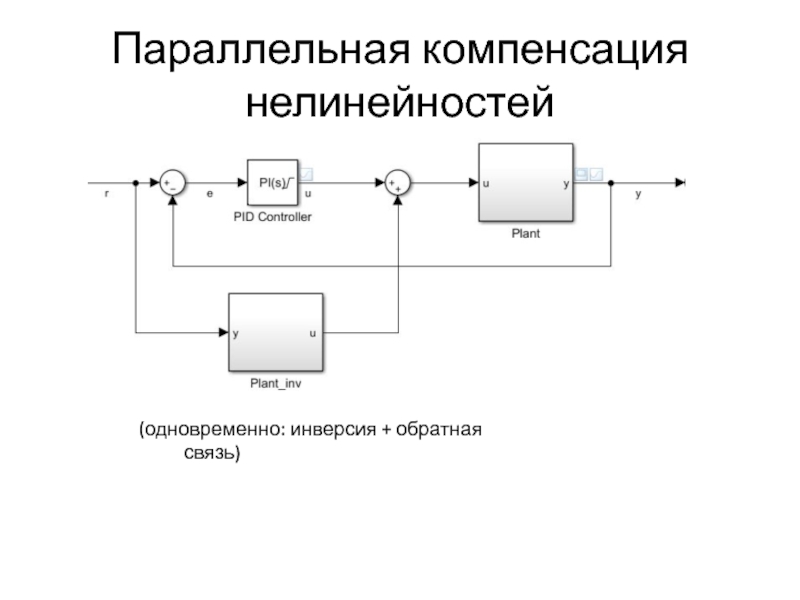
- 28. Параллельная компенсация нелинейностей (одновременно: инверсия + обратная связь)
- 29. Что делать с многомерностью Проблема: возможна
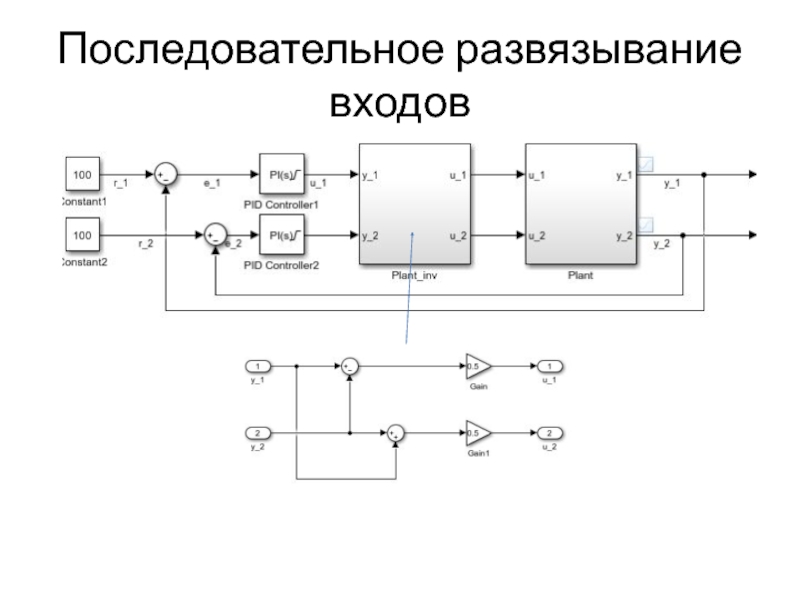
- 30. Последовательное развязывание входов
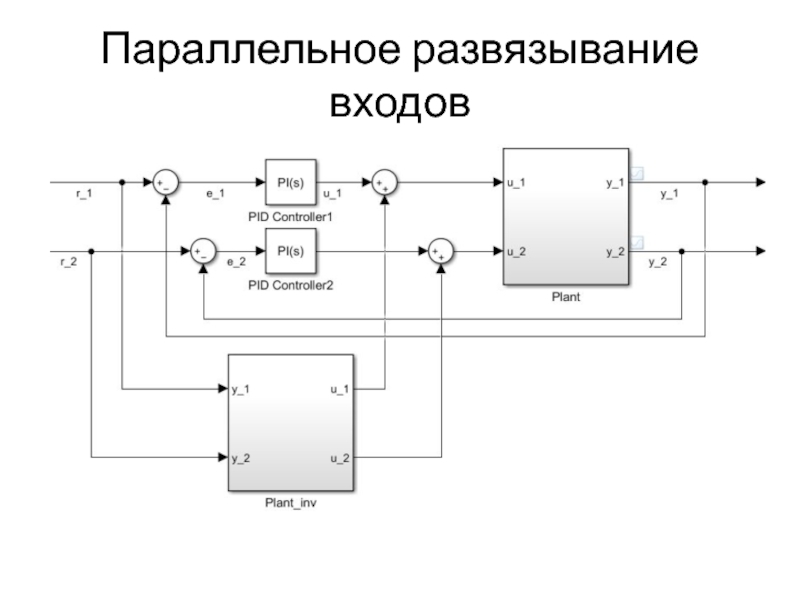
- 31. Параллельное развязывание входов
- 32. Методы из умных книг =) Линейная система
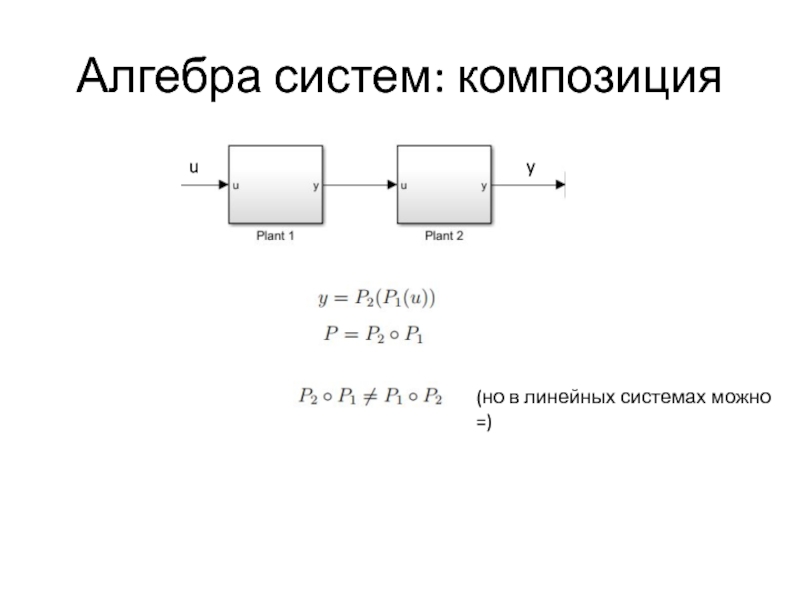
- 33. Алгебра систем: композиция y u (но в линейных системах можно =)
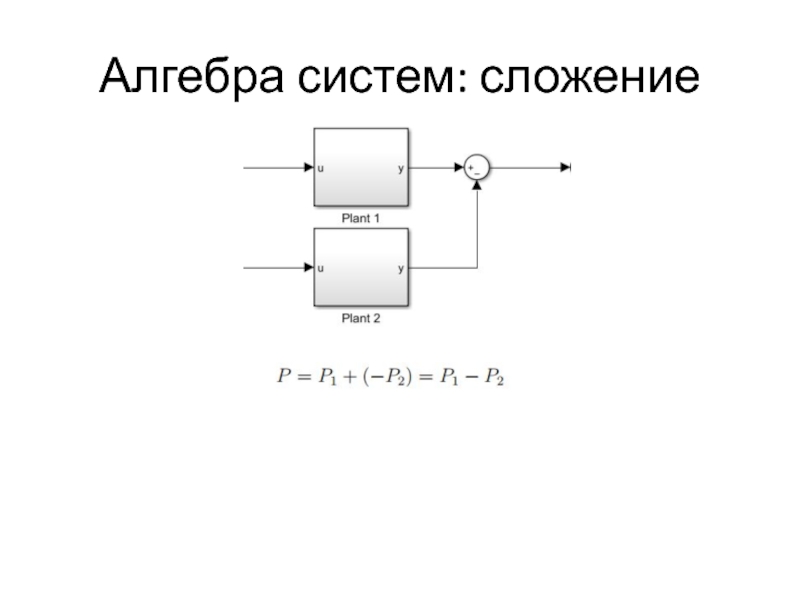
- 34. Алгебра систем: сложение
- 35. Алгебра систем: нейтральные элементы Нейтральный элемент относительно
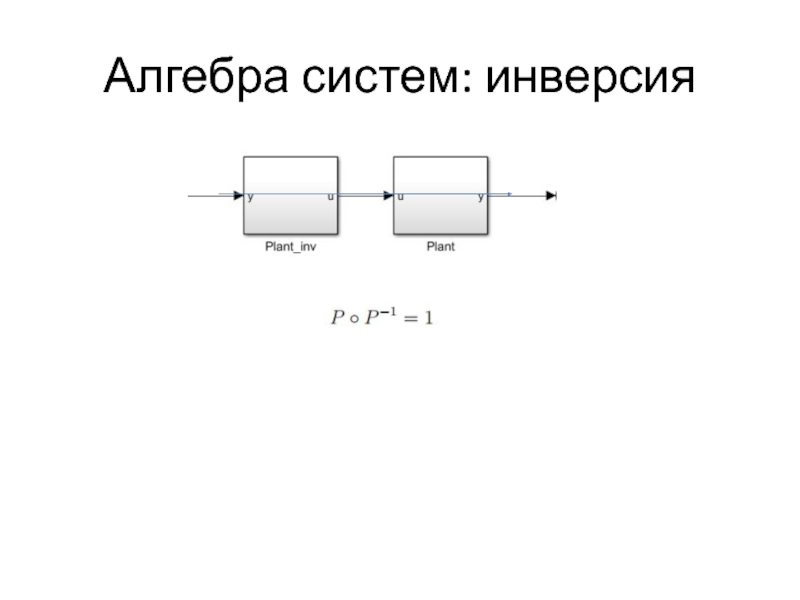
- 36. Алгебра систем: инверсия
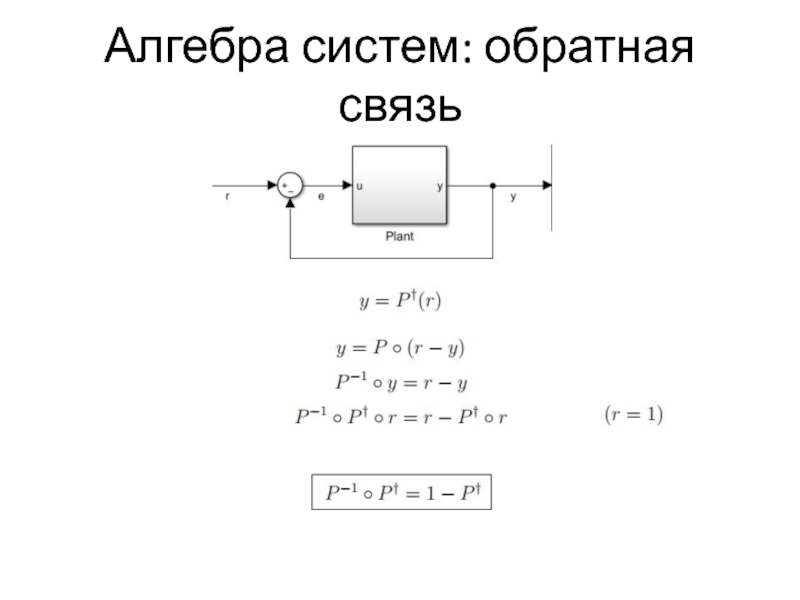
- 37. Алгебра систем: обратная связь
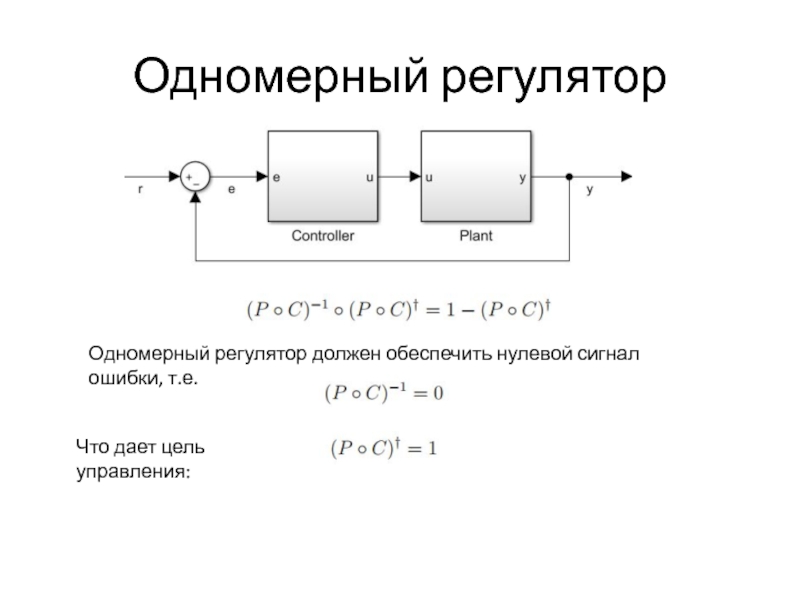
- 38. Одномерный регулятор Одномерный регулятор должен обеспечить нулевой сигнал ошибки, т.е. Что дает цель управления:
- 39. Почитать перед сном =) Олсон Г. Пиани
- 40. Если есть вопросы alex.borysevych@gmail.com Alex Borisevich (LinkedIn, Facebook)
Слайд 2Содержание
Что такое ТАУ
Классификация сущностей ТАУ
Кое-что об алгебре систем
Одномерные регуляторы
Что делать с
Что делать с многомерностью
Демонстрации в Matlab
Слайд 3О чем это
ТАУ = наука преобразовании систем
В идеале – об инвертировании
ТАУ рассматривает как изменить поведение системы за счет подключения внешних связей и систем ("системы управления") к заранее заданной системе ("объекту управления")
ТАУ – это компьютерная наука, для понимания которой надо забыть о физических размерностях сигналов (они там не сохраняются как, например, в физике)!
Слайд 5Гимн черному ящику =)
Стандартная нотация (у них =):
P – "plant" –
С – "controller" – система управления
y(t) – выход
u(t) – вход
x(t) – внутреннее состояние системы
r(t) – "reference" – желаемое состояние выхода
e(t) – "error" – сигнал ошибки между желаемым и действительным
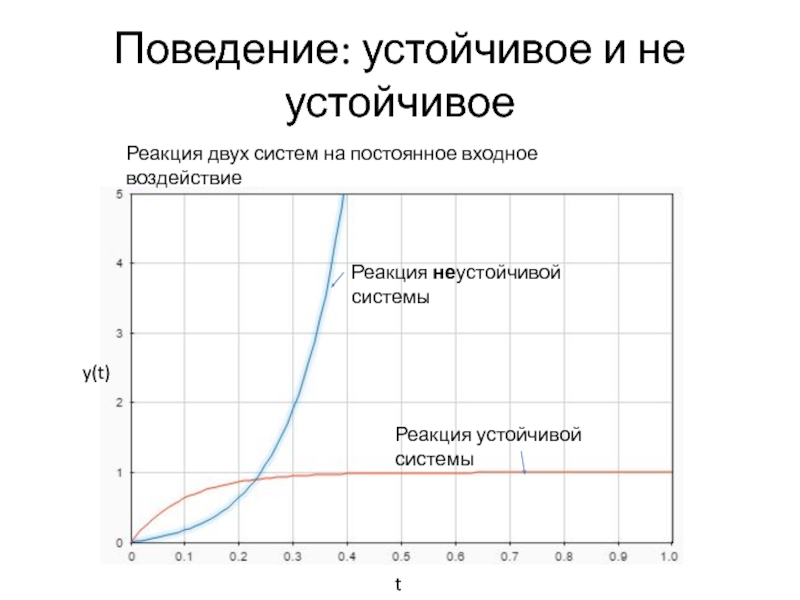
Слайд 11Поведение: устойчивое и не устойчивое
Реакция двух систем на постоянное входное воздействие
Реакция
Реакция неустойчивой системы
t
y(t)
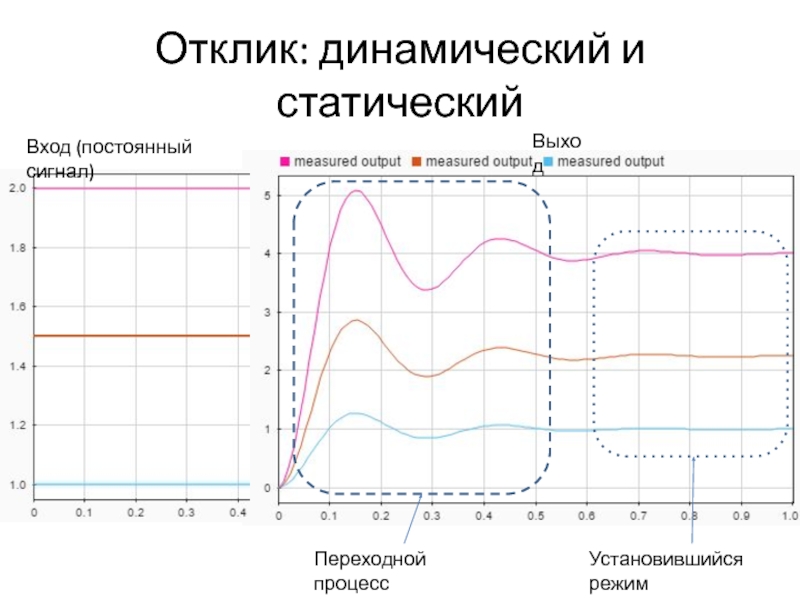
Слайд 12Отклик: динамический и статический
Вход (постоянный сигнал)
Выход
Переходной процесс
(transient)
Установившийся режим
(steady state)
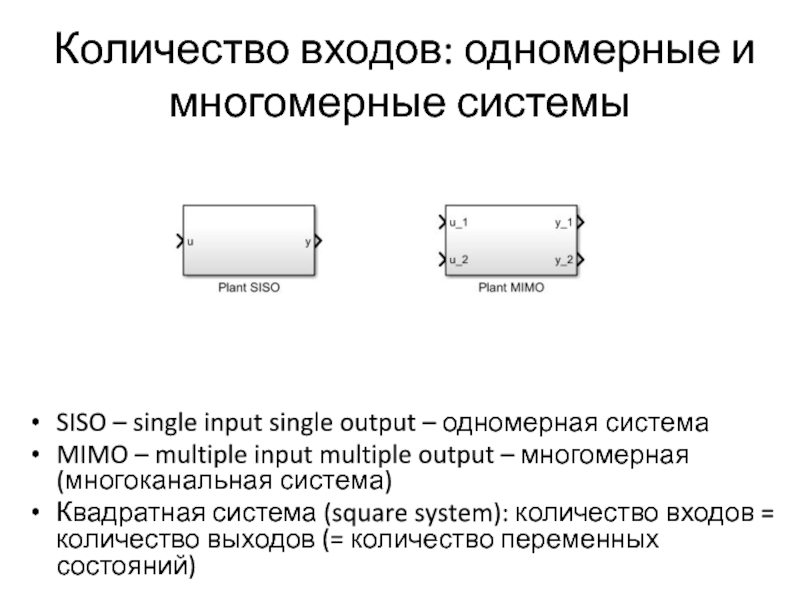
Слайд 13Количество входов: одномерные и многомерные системы
SISO – single input single output
MIMO – multiple input multiple output – многомерная (многоканальная система)
Квадратная система (square system): количество входов = количество выходов (= количество переменных состояний)
Слайд 14Линейные и нелинейные системы
Линейная система
Нелинейная система
Формализм:
Методы исследования:
Преобразование Лапласа,
матричный анализ
Дифференциальная геометрия, топология,
Установившийся режим:
вектора
матрицы
векторные поля
Отклик системы:
вектор постоянных значений
все что угодно =)
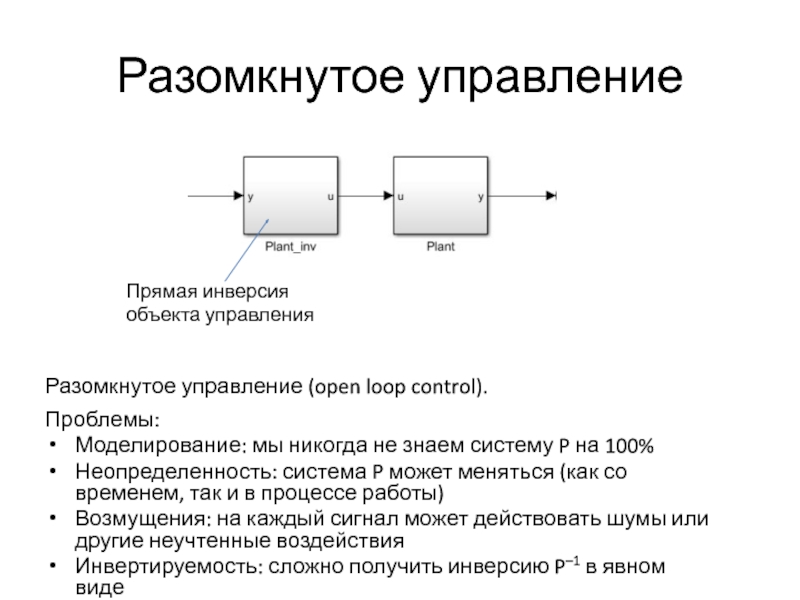
Слайд 15Разомкнутое управление
Проблемы:
Моделирование: мы никогда не знаем систему P на 100%
Неопределенность:
Возмущения: на каждый сигнал может действовать шумы или другие неучтенные воздействия
Инвертируемость: сложно получить инверсию P–1 в явном виде
Разомкнутое управление (open loop control).
Прямая инверсия объекта управления
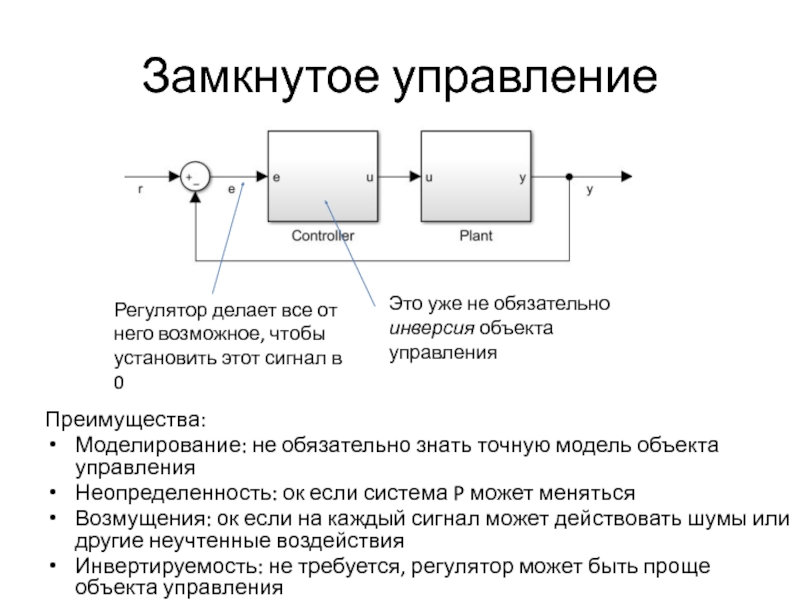
Слайд 17Замкнутое управление
Это уже не обязательно инверсия объекта управления
Регулятор делает все от
Преимущества:
Моделирование: не обязательно знать точную модель объекта управления
Неопределенность: ок если система P может меняться
Возмущения: ок если на каждый сигнал может действовать шумы или другие неучтенные воздействия
Инвертируемость: не требуется, регулятор может быть проще объекта управления
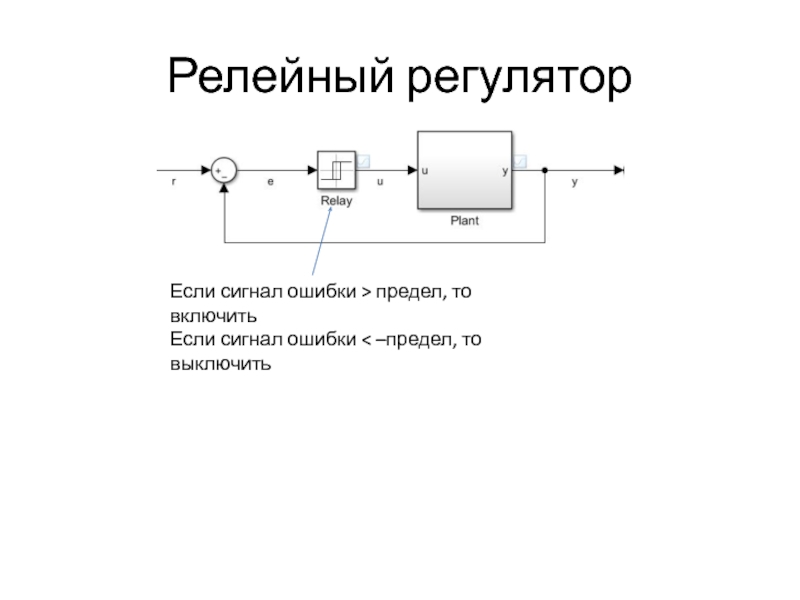
Слайд 18Релейный регулятор
Если сигнал ошибки > предел, то включить
Если сигнал ошибки
Слайд 20Непрерывный регулятор – соображения
Чем дальше я от цели (чем больше сигнал
Слайд 24Алгоритм применения и настройки ПИД-регулятора
Убедиться, что объект управления имеет прямую характеристику:
Установить все коэффициенты в 0, кроме Kp
Подавая на вход r желаемое постоянное значение и перезапуская систему, увеличивать Kp от очень малых значений (близких к 0) до момента когда либо будет достигнута желаемая точность регулирования, либо когда начнутся колебания на выходе
Если наблюдаются колебания, а точность регулирования не достигнута – то добавить интегрального компонента Ki
Если после включения интегрального компонента (Ki > 0) наблюдается перерегулирование – добавить немного Kd
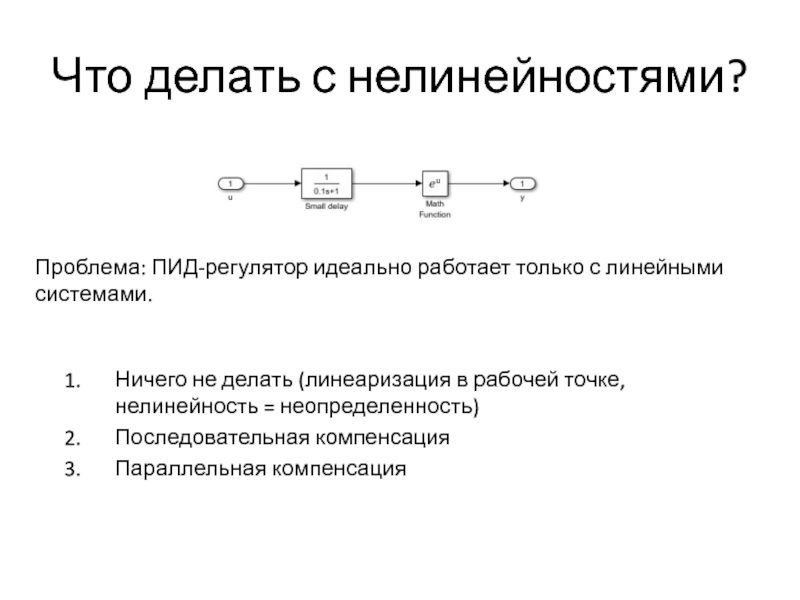
Слайд 26Что делать с нелинейностями?
Ничего не делать (линеаризация в рабочей точке, нелинейность
Последовательная компенсация
Параллельная компенсация
Проблема: ПИД-регулятор идеально работает только с линейными системами.
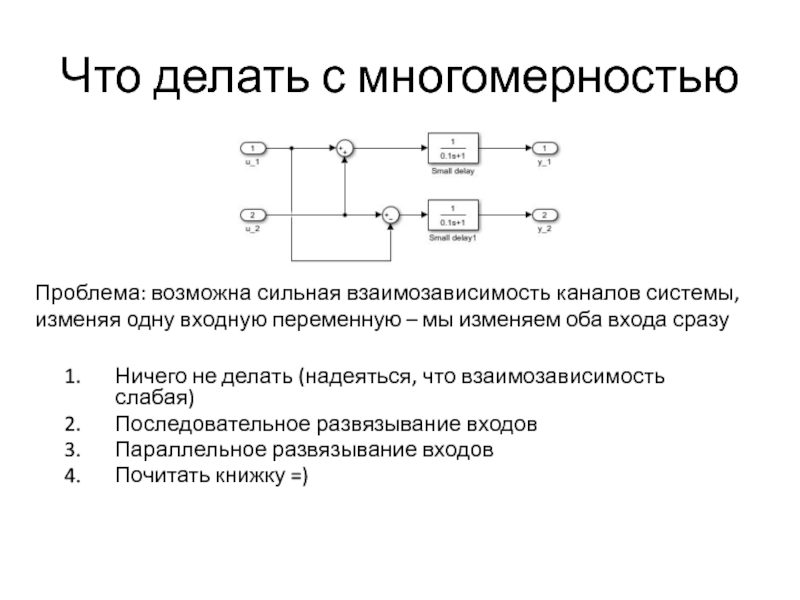
Слайд 29Что делать с многомерностью
Проблема: возможна сильная взаимозависимость каналов системы, изменяя
Ничего не делать (надеяться, что взаимозависимость слабая)
Последовательное развязывание входов
Параллельное развязывание входов
Почитать книжку =)
Слайд 32Методы из умных книг =)
Линейная система
Нелинейная аффинная система
Метод размещения полюсов (pole
1. Система должна быть управляемой.
2. Если значения вектора x не доступны – можно сделать наблюдатель по y (+ система должна быть наблюдаемой).
Метод линеаризации по обратной связи (feedback linearization) :
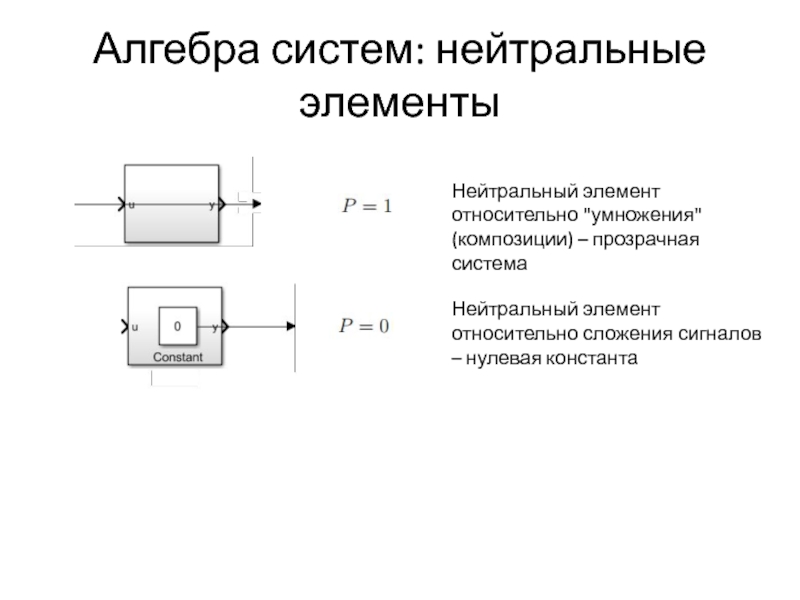
Слайд 35Алгебра систем: нейтральные элементы
Нейтральный элемент относительно "умножения" (композиции) – прозрачная система
Нейтральный
Слайд 38Одномерный регулятор
Одномерный регулятор должен обеспечить нулевой сигнал ошибки, т.е.
Что дает цель
Слайд 39Почитать перед сном =)
Олсон Г. Пиани Дж. Цифровые системы автоматизации и
Мирошник И.В. Теория автоматического управления. Линейные системы. СПб: Питер, 2005. 336 с.
Мирошник И.В. Теория автоматического управления. Нелинейные и оптимальные системы. СПб: Питер, 2006. 271 с.
Борисевич A.B. Теория автоматического управления: элементарное введение с применением MATLAB. СПб.: Издательство СПбГПУ, 2011. 199 с.