- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теоретические основы информатики. Представление информации. (Глава 1.3) презентация
Содержание
- 1. Теоретические основы информатики. Представление информации. (Глава 1.3)
- 2. Лекция 3. Представление информации 1.3.1. Понятие о
- 3. 1.3.1. Понятие о формальном языке 1.3. Представление
- 4. 1.3.1. Понятие о формальном языке 1.3. Представление
- 5. 1.3.1. Понятие о формальном языке 1.3. Представление
- 6. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 7. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 8. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 9. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 10. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 11. 1.3.2. Язык чисел (системы счисления) Примеры арифметических
- 12. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 13. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 14. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 15. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 16. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 17. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 18. 1.3.2. Язык чисел (системы счисления) Примеры арифметических
- 19. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 20. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 21. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 22. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 23. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 24. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 25. 1.3.2. Язык чисел (системы счисления) Примеры арифметических
- 26. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 27. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 28. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 29. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 30. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 31. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 32. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 33. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 34. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 35. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 36. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 37. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 38. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 39. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 40. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 41. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 42. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 43. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 44. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 45. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 46. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 47. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 48. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 49. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 50. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 51. 1.3.2. Язык чисел (системы счисления) 1.3. Представление
- 52. 1.3.3. Язык логики 1.3. Представление информации Высказывания
- 53. 1.3.3. Язык логики 1.3. Представление информации Логические
- 54. 1.3.3. Язык логики 1.3. Представление информации Основные
- 55. 1.3.3. Язык логики 1.3. Представление информации Логическое
- 56. 1.3.3. Язык логики Логическое сложение — логическая
- 57. 1.3.3. Язык логики Логическое умножение — логическая
- 58. 1.3.3. Язык логики 1.3. Представление информации
- 59. 1.3.3. Язык логики 1.3. Представление информации
- 60. 1.3.3. Язык логики 1.3. Представление информации
- 61. 1.3.3. Язык логики 1.3. Представление информации
- 62. 1.3.3. Язык логики 1.3. Представление информации
- 63. 1.3.3. Язык логики 1.3. Представление информации
- 64. 1.3.3. Язык логики 1.3. Представление
- 65. 1.3.3. Язык логики 1.3. Представление информации
- 66. 1.3.3. Язык логики 1.3. Представление информации
- 67. 1.3.3. Язык логики 1.3. Представление информации
- 68. 1.3.3. Язык логики 1.3. Представление информации
- 69. 1.3.3. Язык логики Аксиомы алгебры логики 1.3. Представление информации
- 70. 1.3.3. Язык логики Свойства дизъюнкции и конъюнкции
- 71. 1.3.3. Язык логики Законы алгебры логики 1.3.
- 72. 1.3.3. Язык логики 1.3. Представление информации
- 73. 1.3.3. Язык логики 1.3. Представление информации
- 74. 1.3.3. Язык логики 1.3. Представление информации
- 75. 1.3.3. Язык логики Виды логических электронных схем
- 76. 1.3.3. Язык логики Построение логических электронных схем
- 77. 1.3.3. Язык логики Этапы построения логических электронных
- 78. 1.3.3. Язык логики Обозначения логических функций на
- 79. 1.3.3. Язык логики 1.3. Представление информации
- 80. 1.3.3. Язык логики 1.3. Представление информации
- 81. 1.3.3. Язык логики 1.3. Представление информации
- 82. 1.3.3. Язык логики 1.3. Представление информации
- 83. 1.3.3. Язык логики 1.3. Представление информации
- 84. 1.3.3. Язык логики Сложные высказывания и сложные
- 85. 1.3.3. Язык логики Пример табличного задания логической
- 86. 1.3.3. Язык логики Логический базис 1.3. Представление
- 87. 1.3.3. Язык логики Конъюнктивные и дизъюнктивные термы
- 88. 1.3.3. Язык логики Конъюнктивные и дизъюнктивные нормальные
- 89. 1.3.3. Язык логики Алгоритм получения СДНФ из
- 90. 1.3.3. Язык логики Алгоритм получения СКНФ из
- 91. 1.3.3. Язык логики 1.3. Представление информации
- 92. 1.3.3. Язык логики 1.3. Представление информации
- 93. 1.3.3. Язык логики 1.3. Представление информации
- 94. 1.3.3. Язык логики 1.3. Представление информации
- 95. 1.3.3. Язык логики 1.3. Представление информации
- 96. 1.3.3. Язык логики 1.3. Представление информации
- 97. 1.3.3. Язык логики Временные булевы функции 1.3.
Слайд 1Глава 1. Теоретические основы информатики
Лекция 1. Информация и общество
Лекция 2. Информация
Лекция
Лекция 4. Информационные процессы
Лекция 5. ЭВМ — техническое средство информатики
Слайд 2Лекция 3. Представление информации
1.3.1. Понятие о формальном языке
1.3.2. Язык чисел (системы
1.3.3. Язык логики
Московский государственный университет информатики и программирования
Глава 1. Теоретические основы информатики
Слайд 31.3.1. Понятие о формальном языке
1.3. Представление информации
Символьная и образная информация
Символьная информация
Образная информация — это сохраненные в памяти ощущения человека от контакта с источником, воспринимаемые всеми органами чувств человека.
Слайд 41.3.1. Понятие о формальном языке
1.3. Представление информации
Классификация языков
Язык — это определенная система
Слайд 51.3.1. Понятие о формальном языке
1.3. Представление информации
Естественные и формальные языки
Естественные языки —
Формальные языки — это искусственно созданные языки для профессионального применения.
Для любого языка можно выделить:
– алфавит — множество используемых символов;
– синтаксис — правила записи языковых конструкций (текста на языке);
– семантика — смысловая сторона языковых конструкций;
– прагматика — практические последствия применения текста на данном языке.
Слайд 61.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Системы счисления
Система счисления — это правила
Унарная
Непозиционная
Позиционная
Унарная система счисления — это система счисления, в которой для записи чисел используется только один знак.
Непозиционная система счисления — каждой цифре в любом месте числа соответствует одно и то же значение — количественный эквивалент.
Позиционная система счисления — значение каждой цифры в изображении числа определяется ее положением (позицией) в ряду других цифр.
Слайд 71.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Непозиционная система счисления — римская система
Базовые числа:
1 — I
5 — V
10 — X
50 — L
100 — C
500 — D
1000 — M
Правила записи чисел:
– если цифра меньшего значения стоит справа от большей цифры, то их значения суммируются; если слева — то меньшее значение вычитается из большего;
– цифры «I», «X», «C» и «M» могут следовать подряд не более трех раз каждая;
– цифры «V», «L», «D» могут использоваться в записи не более одного раза.
Слайд 81.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Позиционная система счисления
Алфавитом системы счисления
Основанием системы счисления (величиной алфавита данной системы счисления) называется величина p, равная отношению веса любого разряда числа к весу соседнего младшего разряда.
Базис позиционной системы счисления — это последовательность чисел, каждое из которых задает вес каждого разряда.
Десятичная система счисления:
– алфавит — «0», «1», «2», «3», «4», «5», «6», «7», «8», «9».
– основание системы счисления — 10.
– базис позиционной системы счисления —
…; 0,001; 0,01; 0,1; 1; 10; 100; …
Слайд 91.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Сущность позиционного представления чисел
Слайд 101.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Двоичная система счисления:
– алфавит — «0»,
– основание системы счисления — 2.
– базис позиционной системы счисления —
…; 1/16; 1/8; 1/4; 1/2; 1; 2; 4; 8; …
Таблица сложения, вычитания и умножения в двоичной системе счисления
Слайд 111.3.2. Язык чисел (системы счисления)
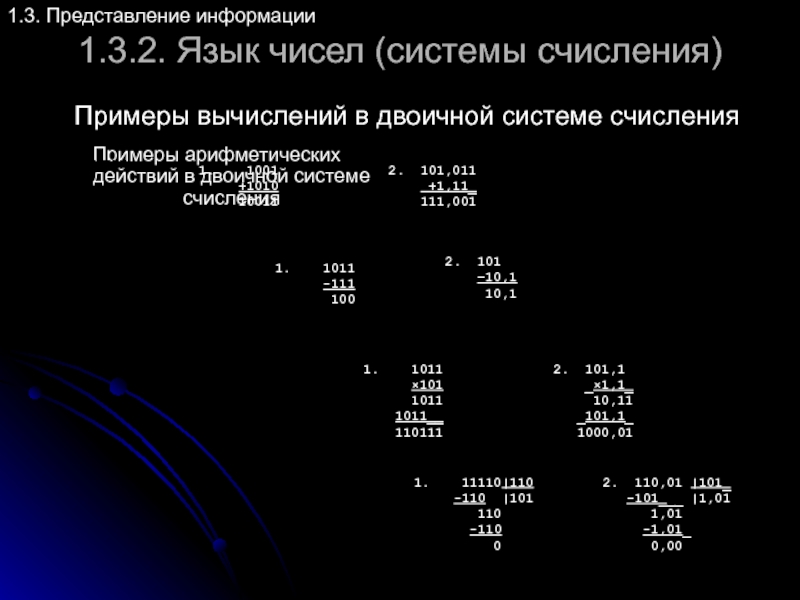
Примеры арифметических действий в двоичной системе счисления
1.3.
1. 1001
+1010
10011
2. 101,011
+1,11_
111,001
1. 1011
-111
100
2. 101
–10,1
10,1
1. 1011
×101
1011
1011__
110111
2. 101,1
_×1,1_
10,11
_101,1_
1000,01
1. 11110|110
-110 |101
110
-110
0
2. 110,01 |101_
-101___ |1,01
1,01
-1,01_
0,00
Примеры вычислений в двоичной системе счисления
Слайд 121.3.2. Язык чисел (системы счисления)
1.3. Представление информации
а. 11101,11
+ 101,1_
б. 10000
– 11,011
в. 101,11
×_11,01_
г. 1001011,11001|11001
|
Примеры для самостоятельного решения
1. Записать числа в виде многочлена и схемы Горнера и вычислить их в десятичной системе счисления:
2. Вычислить в двоичной системе счисления:
Слайд 131.3.2. Язык чисел (системы счисления)
1.3. Представление информации
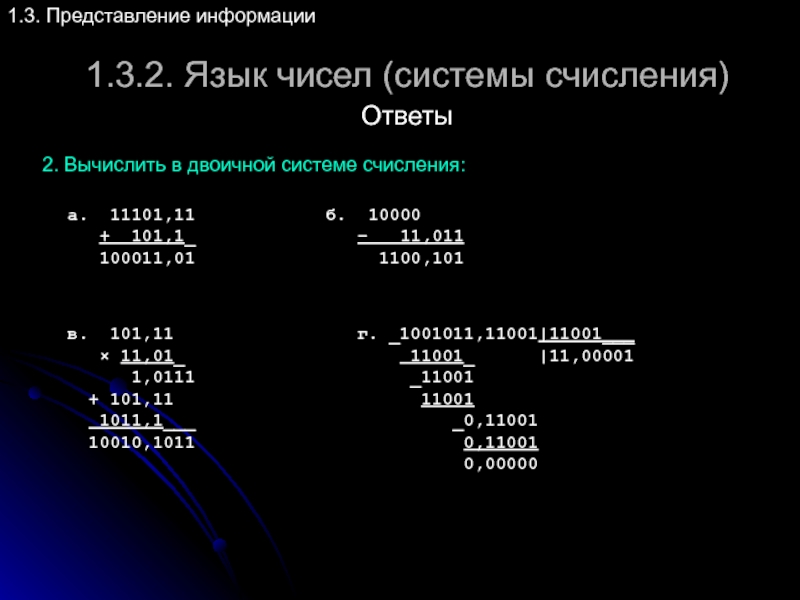
Ответы
1. Записать числа в виде
Слайд 141.3.2. Язык чисел (системы счисления)
1.3. Представление информации
а. 11101,11
+ 101,1_
б. 10000
– 11,011
1100,101
в. 101,11
× 11,01_
1,0111
+ 101,11
1011,1___
10010,1011
г. _1001011,11001|11001___
11001_ |11,00001
_11001
11001
_0,11001
0,11001
0,00000
Ответы
2. Вычислить в двоичной системе счисления:
Слайд 151.3.2. Язык чисел (системы счисления)
1.3. Представление информации
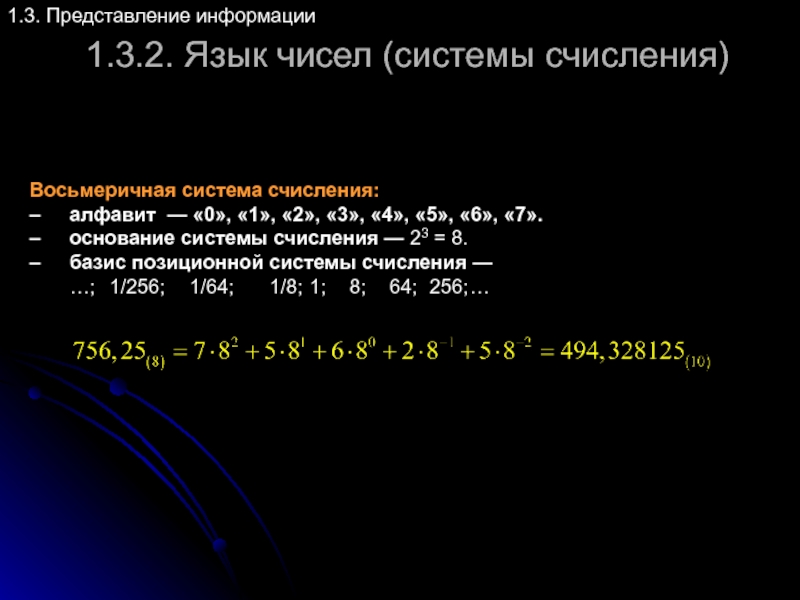
Восьмеричная система счисления:
– алфавит — «0»,
– основание системы счисления — 23 = 8.
– базис позиционной системы счисления —
…; 1/256; 1/64; 1/8; 1; 8; 64; 256; …
Слайд 161.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Таблица сложения в восьмеричной системе
0 1 2 3 4 5 6 7 10
0 | 0 1 2 3 4 5 6 7 10
1 | 1 2 3 4 5 6 7 10 11
2 | 2 3 4 5 6 7 10 11 12
3 | 3 4 5 6 7 10 11 12 13
4 | 4 5 6 7 10 11 12 13 14
5 | 5 6 7 10 11 12 13 14 15
6 | 6 7 10 11 12 13 14 15 16
7 | 7 10 11 12 13 14 15 16 17
10| 10 11 12 13 14 15 16 17 20
Слайд 171.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Таблица умножения в восьмеричной системе
0 1 2 3 4 5 6 7 10
0 | 0 0 0 0 0 0 0 0 0
1 | 0 1 2 3 4 5 6 7 10
2 | 0 2 4 6 10 12 14 16 20
3 | 0 3 6 11 14 17 22 25 30
4 | 0 4 10 14 20 24 30 34 40
5 | 0 5 12 17 24 31 36 43 50
6 | 0 6 14 22 30 36 44 52 60
7 | 0 7 16 25 34 43 52 61 70
10| 0 10 20 30 40 50 60 70 100
Слайд 181.3.2. Язык чисел (системы счисления)
Примеры арифметических действий в двоичной системе счисления
1.3.
1. 367
+1254
1643
2. 652,33
+6,7_
661,23
1. 3117
- 632
2265
2. 452
-_20,6
431,2
1. 75
×321
75
+ 172
267__
30715
2. 51,6
×4,2_
12,34
+247,0_
261,34
1. _334|24
24 |13
_74
74
0
2. _3,52 |2,2
2,2 |1,5
_1,32
1,32
0
Примеры вычислений в восьмеричной системе счисления
Слайд 191.3.2. Язык чисел (системы счисления)
1.3. Представление информации
а. 163,54
+
б. _725
51,7
в. 11,62
×_7,4_
г. 15,52|2,3
|
Примеры для самостоятельного решения
1. Записать числа в виде многочлена и схемы Горнера и вычислить их в десятичной системе счисления:
2. Вычислить в восьмеричной системе счисления:
Слайд 201.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Ответы
1. Записать числа в виде
Слайд 211.3.2. Язык чисел (системы счисления)
1.3. Представление информации
а. 163,54
+
242,07
б. _725
51,7
653,1
в. 11,62
×_7,4_
4,710
+104,36_
111,27
г. _15,52|2,3
13,7_|5,6
_1,62
1,62
0,00
Ответы
2. Вычислить в восьмеричной системе счисления:
Слайд 221.3.2. Язык чисел (системы счисления)
1.3. Представление информации
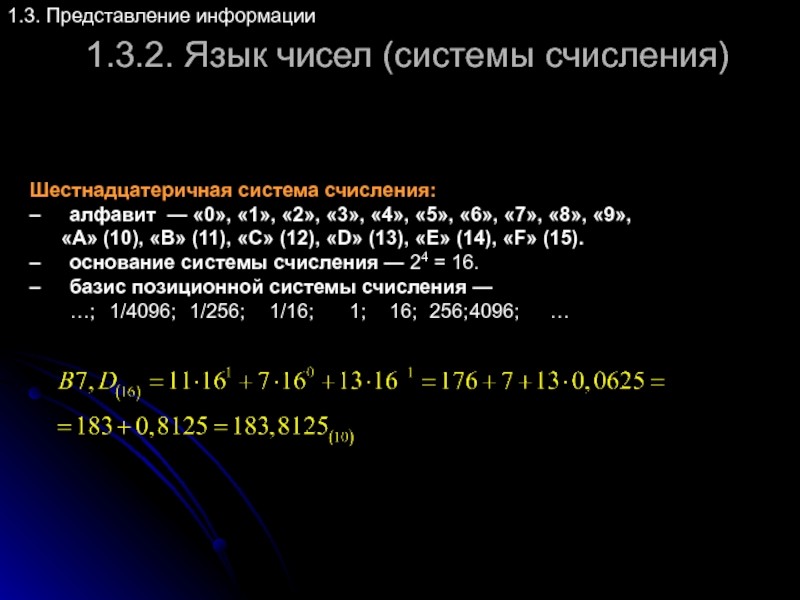
Шестнадцатеричная система счисления:
– алфавит — «0»,
– основание системы счисления — 24 = 16.
– базис позиционной системы счисления —
…; 1/4096; 1/256; 1/16; 1; 16; 256; 4096; …
Слайд 231.3.2. Язык чисел (системы счисления)
1.3. Представление информации
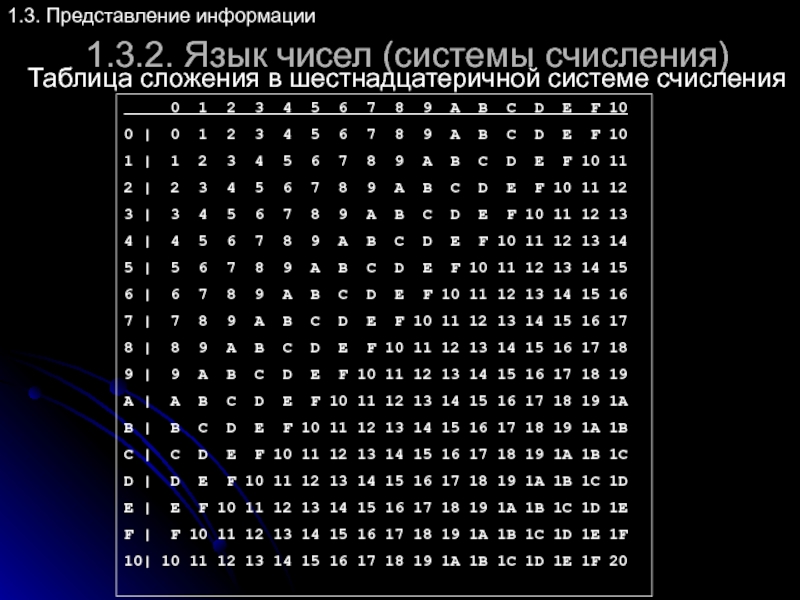
Таблица сложения в шестнадцатеричной системе
0 1 2 3 4 5 6 7 8 9 A B C D E F 10
0 | 0 1 2 3 4 5 6 7 8 9 A B C D E F 10
1 | 1 2 3 4 5 6 7 8 9 A B C D E F 10 11
2 | 2 3 4 5 6 7 8 9 A B C D E F 10 11 12
3 | 3 4 5 6 7 8 9 A B C D E F 10 11 12 13
4 | 4 5 6 7 8 9 A B C D E F 10 11 12 13 14
5 | 5 6 7 8 9 A B C D E F 10 11 12 13 14 15
6 | 6 7 8 9 A B C D E F 10 11 12 13 14 15 16
7 | 7 8 9 A B C D E F 10 11 12 13 14 15 16 17
8 | 8 9 A B C D E F 10 11 12 13 14 15 16 17 18
9 | 9 A B C D E F 10 11 12 13 14 15 16 17 18 19
A | A B C D E F 10 11 12 13 14 15 16 17 18 19 1A
B | B C D E F 10 11 12 13 14 15 16 17 18 19 1A 1B
C | C D E F 10 11 12 13 14 15 16 17 18 19 1A 1B 1C
D | D E F 10 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D
E | E F 10 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D 1E
F | F 10 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D 1E 1F
10| 10 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D 1E 1F 20
Слайд 241.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Таблица умножения в шестнадцатеричной системе
0 1 2 3 4 5 6 7 8 9 A B C D E F 10
0 | 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 | 0 1 2 3 4 5 6 7 8 9 A B C D E F 10
2 | 0 2 4 6 8 A C E 10 12 14 16 18 1A 1C 1E 20
3 | 0 3 6 9 C F 12 15 18 1B 1E 21 24 27 2A 2D 30
4 | 0 4 8 C 10 14 18 1C 20 24 28 2C 30 34 38 3C 40
5 | 0 5 A F 14 19 1E 23 28 2D 32 37 3C 41 46 4B 50
6 | 0 6 C 12 18 1E 24 2A 30 36 3C 42 48 4E 54 5A 60
7 | 0 7 E 15 1C 23 2A 31 38 3F 46 4D 54 5B 62 69 70
8 | 0 8 10 18 20 28 30 38 40 48 50 58 60 68 70 78 80
9 | 0 9 12 1B 24 2D 36 3F 48 51 5A 63 6C 75 7E 87 90
A | 0 A 14 1E 28 32 3C 46 50 5A 64 6E 78 82 8C 96 A0
B | 0 B 16 21 2C 37 42 4D 58 63 6E 79 84 8F 9A A5 B0
C | 0 C 18 24 30 3C 48 54 60 6C 78 84 90 9C A8 B4 C0
D | 0 D 1A 27 34 41 4E 5B 68 75 82 8F 9C A9 B6 C3 D0
E | 0 E 1C 2A 38 46 54 62 70 7E 8C 9A A8 B6 C4 D2 E0
F | 0 F 1E 2D 3C 4B 5A 69 78 87 96 A5 B4 C3 D2 E1 F0
10| 0 10 20 30 40 50 60 70 80 90 A0 B0 C0 D0 E0 F0 100
Слайд 251.3.2. Язык чисел (системы счисления)
Примеры арифметических действий в двоичной системе счисления
1.3.
1. 1A9
+21F3
239C
2. AF,0E
+3,7_
B2,7E
1. 3117
- 632
2AE5
2. 45D
-_AA,6
3B2,A
1. 1A
×BCD
152
+ 138
11E__
132D2
2. 5D,6
×A,2_
B,AC
+3A5,C_
3B1,6C
1. _1B0B|2B
1AE |A1
_2B
2B
0
2. _27,9C|3,4
27,0 |C,3
_0,9C
0,9C
0,00
Примеры вычислений в шестнадцатеричной системе счисления
Слайд 261.3.2. Язык чисел (системы счисления)
1.3. Представление информации
а. 2DE,A5
+
б. _725
FA,7
в. DA,65
×_A,F_
г. 2F,5A|1,D
|
Примеры для самостоятельного решения
1. Записать числа в виде многочлена и схемы Горнера и вычислить их в десятичной системе счисления:
2. Вычислить в шестнадцатеричной системе счисления:
Слайд 271.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Ответы
1. Записать числа в виде
Слайд 281.3.2. Язык чисел (системы счисления)
1.3. Представление информации
а. 2DE,A5
+
2EF,E34
б. _725
FA,7
62A,9
в. DA,65
×_A,F__
CC,BEB
+887,F2_
954,BOB
г. _2F,5A|1,D_
1D__ |1A,2
_12,5
12,2
_0,3A
0,3A
0,00
Ответы
2. Вычислить в шестнадцатеричной системе счисления:
Слайд 291.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Двоично-десятичная система счисления:
– алфавит в виде
– основание системы счисления — 10.
– базис позиционной системы счисления —
…; 0,001; 0,01; 0,1; 1; 10; 100; 1000; …
Используется как вспомогательная система счисления в компьютере
Слайд 301.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Схема перевода чисел из одной
q-ая система счисления
p-ая система счисления
Арифметика q-ой или
p-ой системы счисления
q-ая система счисления
p-ая система счисления
Арифметика 10-ой системы счисления
10-ая система счисления
Арифметика 10-ой системы счисления
Слайд 311.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Перевод чисел из q-ой системы
Целая часть
Дробная часть
1. Каждая цифра числа в q-ой системе счисления переводится в число в десятичной системе счисления — в .
Полученные числа нумеруются справа налево, начиная с нуля — .
3. Десятичное число, соответствующее i-ой цифре исходного числа, умножается на , где i — номер цифры в исходном числе, и результаты произведений складываются.
1. Каждая цифра числа в q-ой системе счисления переводится в число в десятичной системе счисления.
Полученные числа нумеруются cлева направо, начиная с единицы —
3. Десятичное число, соответствующее i-ой цифре исходного числа, умножается на , где k — номер цифры в исходном числе, и результаты произведений складываются.
Слайд 321.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Перевод чисел из q-ой системы
B0F9(16)
1.
2.
3.
0,B0F9(16)
1.
2.
3.
Слайд 331.3.2. Язык чисел (системы счисления)
1.3. Представление информации
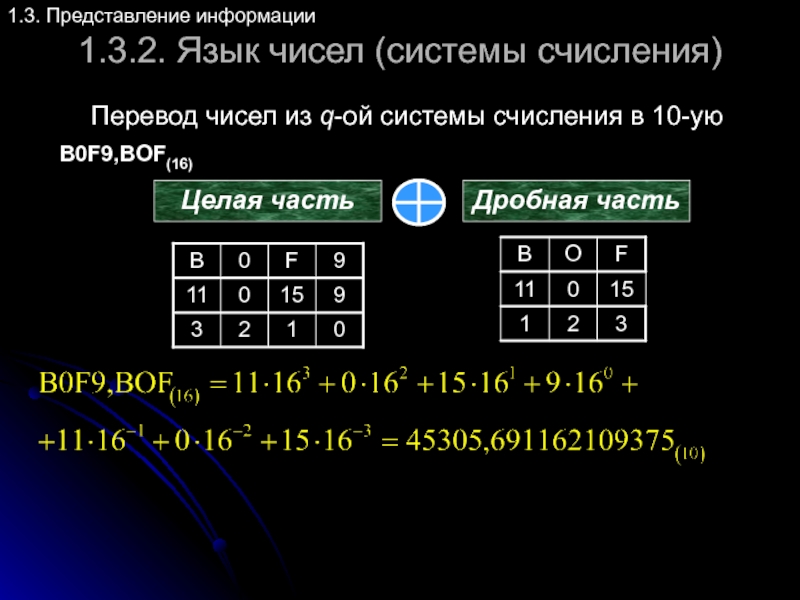
Перевод чисел из q-ой системы
B0F9,BOF(16)
Целая часть
Дробная часть
Слайд 341.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Примеры для самостоятельного решения
1. Перевести
а)
б)
в)
г)
д)
Слайд 351.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Ответы
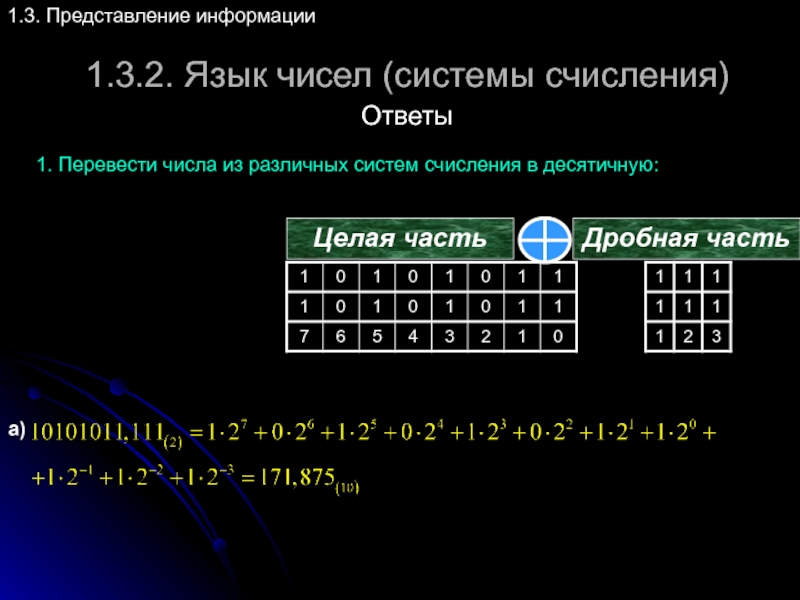
1. Перевести числа из различных
а)
Целая часть
Дробная часть
Слайд 361.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Ответы
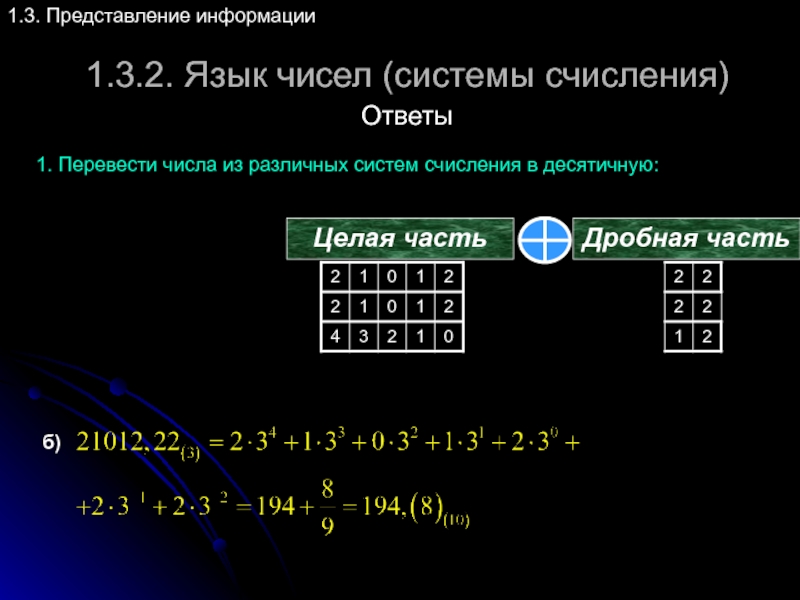
1. Перевести числа из различных
Целая часть
Дробная часть
б)
Слайд 371.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Ответы
1. Перевести числа из различных
Целая часть
Дробная часть
в)
Слайд 381.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Ответы
1. Перевести числа из различных
Целая часть
Дробная часть
г)
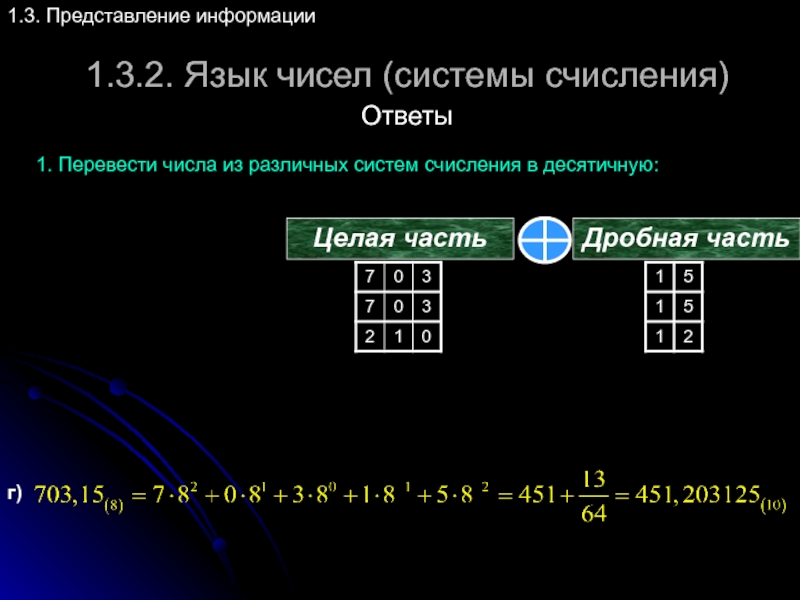
Слайд 391.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Ответы
1. Перевести числа из различных
Целая часть
Дробная часть
д)
Слайд 401.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Перевод чисел из 10-ой системы
Целая часть
Дробная часть
1. Делим исходное число A на p (основание новой системы счисления) нацело и записываем в качестве нового значения числа A целую часть результата от деления.
2. Остаток от деления образует соответствующую цифру в p-ой системе счисления слева от полученных ранее цифр в p-ой записи числа .
3. Выполняем пункты 1. и 2. до тех пор, пока число A не станет равным нулю.
4. Выписываем ответ в виде полученных остатков в обратном порядке.
1. Умножаем дробную часть исходного числа A на p, целая часть полученного произведения является первой цифрой после запятой в искомом числе (целая часть всегда меньше p).
2. Дробную часть произведения снова умножаем на p, целую часть полученного числа заменяем на цифру в p-ой системе счисления и приписываем ее справа к результату.
3. Выполняем пункт 2. до тех пор, пока дробная часть произведения не станет равной нулю, или не выделится период.
Слайд 411.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Перевод чисел из 10-ой системы
123(10)=?(3)
A | Остаток
123 | 0
41 | 2
13 | 1
4 | 1
1 | 1
0 |
123(10)=11120(3)
0,375(10)=?(2)
Дробная | Целая
часть | часть
0,375 | 0
0,75 | 1
0,5 | 1
0 |
0,375(10)=0,011(2)
Слайд 421.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Примеры для самостоятельного решения
1. Перевести
а)
б)
в)
г)
д)
216,75(10)=?(2)
134,75(10)=?(3)
98,5625(10)=?(8)
19784(10)=?(9)
1456,4375(10)=?(16)
Слайд 431.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Ответы
1. Перевести числа из десятичной
а)
Целая часть
Дробная часть
216,75(10)=11011000,11(2)
A | Остаток
216 | 0
108 | 0
54 | 0
27 | 1
13 | 1
6 | 0
3 | 1
1 | 1
0 |
Дробная | Целая
часть | часть
0,75 | 1
0,5 | 1
0 |
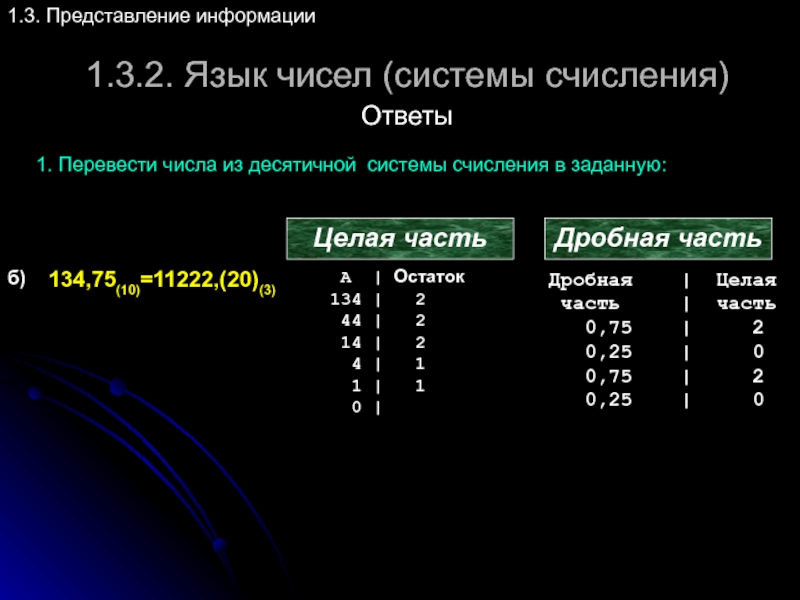
Слайд 441.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Ответы
1. Перевести числа из десятичной
Целая часть
Дробная часть
A | Остаток
134 | 2
44 | 2
14 | 2
4 | 1
1 | 1
0 |
Дробная | Целая
часть | часть
0,75 | 2
0,25 | 0
0,75 | 2
0,25 | 0
б)
134,75(10)=11222,(20)(3)
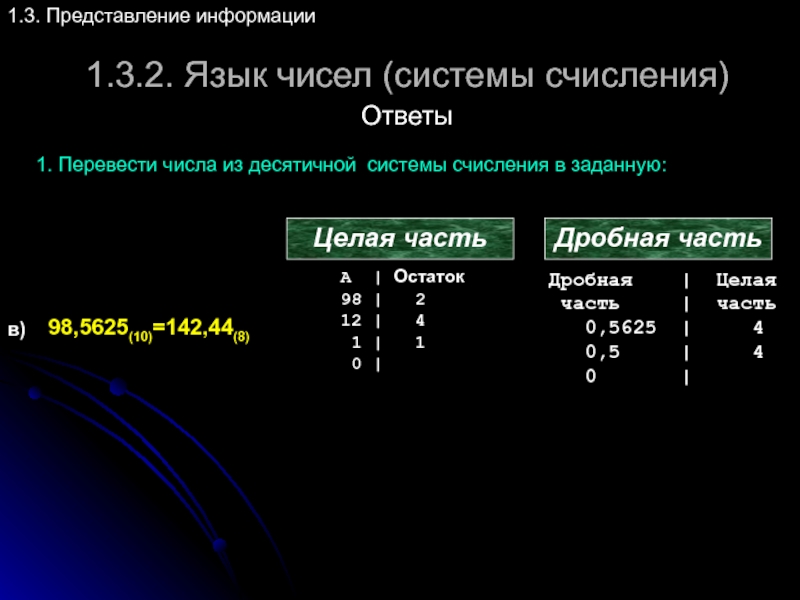
Слайд 451.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Ответы
1. Перевести числа из десятичной
Целая часть
Дробная часть
A | Остаток
98 | 2
12 | 4
1 | 1
0 |
Дробная | Целая
часть | часть
0,5625 | 4
0,5 | 4
0 |
в)
98,5625(10)=142,44(8)
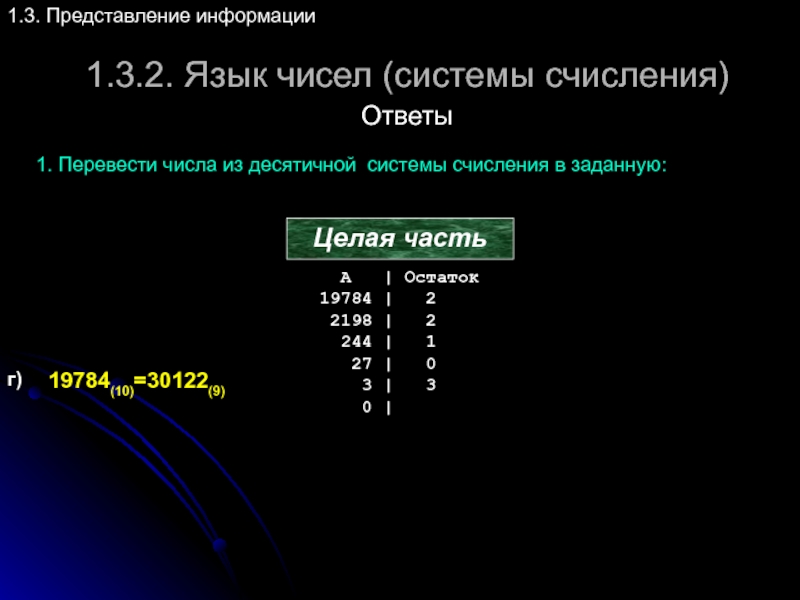
Слайд 461.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Ответы
1. Перевести числа из десятичной
Целая часть
A | Остаток
19784 | 2
2198 | 2
244 | 1
27 | 0
3 | 3
0 |
г)
19784(10)=30122(9)
Слайд 471.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Ответы
1. Перевести числа из десятичной
Целая часть
Дробная часть
A | Остаток
1456 | 0
91 | 11 (B)
5 | 5
0 |
Дробная | Целая
часть | часть
0,4375 | 7
0 |
д)
1456,4375(10)=5B0,7(16)
Слайд 481.3.2. Язык чисел (системы счисления)
1.3. Представление информации
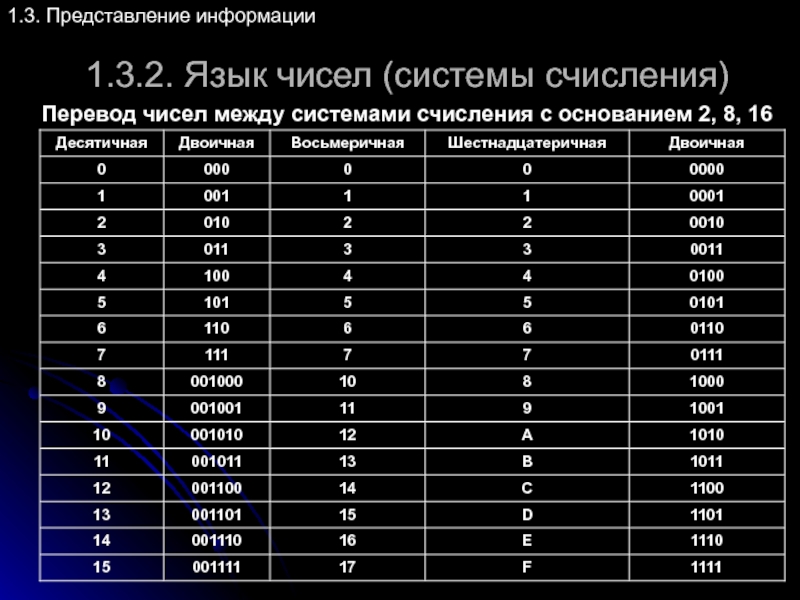
Перевод чисел между системами счисления
Слайд 491.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Перевод чисел между системами счисления
110001(2)=[110][001](2)=61(8)
110001(2)=[0011][0001] (2)=31(16)
D3(16)=[1101][0011] (2)=11010011(2)
D3(16)=[011][010][011] (2)=323(8)
в)
г)
б)
a)
Слайд 501.3.2. Язык чисел (системы счисления)
1.3. Представление информации
Примеры для самостоятельного решения
1. Представить
Слайд 511.3.2. Язык чисел (системы счисления)
1.3. Представление информации
1. Представить числа в заданных
Ответы
Слайд 521.3.3. Язык логики
1.3. Представление информации
Высказывания и высказательные формы
Высказыванием (суждением) называется повествовательное
Логика — наука, изучающая методы установления истинности или ложности одних высказываний на основе истинности или ложности других высказываний. В математической логике содержание рассуждений отбрасывается, а используется только их форма и логическое значение.
Обозначаются высказывания буквами латинского алфавита A, B, C и т. д.
Истинность высказывания выражается через логические величины, принимающие значения:
True — Истина — 1
False — Ложь — 0.
Высказывательной (пропозициональной) формой называется предложение, содержащее хотя бы одну переменную и становящееся высказыванием при подстановке хотя бы одного значения этой переменной.
Слайд 531.3.3. Язык логики
1.3. Представление информации
Логические функции
Функция одной или нескольких переменных, область
Предикат, аргументы которого могут принимать только значения 0 или 1 (определены на множестве {0, 1}) называется булевой функцией.
Математическая функция
Предикат
0
1
Булева функция
0
1
0
1
Булевы функции задаются: 1) аналитически;
2) при помощи таблиц истинности.
Слайд 541.3.3. Язык логики
1.3. Представление информации
Основные логические операции
1. Логическое отрицание
2. Логическое сложение
3. Логическое умножение (конъюнкция)
или
или
Слайд 551.3.3. Язык логики
1.3. Представление информации
Логическое отрицание — логическая операция «НЕ»
Отрицанием высказывания
Таблица истинности
Диаграмма Венна
Изображение на электронных схемах
Слайд 561.3.3. Язык логики
Логическое сложение — логическая операция «ИЛИ»
1.3. Представление информации
Логическое сложение
Таблица истинности
Диаграмма Венна
Изображение на электронных схемах
,
Выход
Вход A
Вход B
1
Слайд 571.3.3. Язык логики
Логическое умножение — логическая операция «И»
1.3. Представление информации
Логическое умножение
Таблица истинности
Диаграмма Венна
Изображение на электронных схемах
,
Выход
Вход A
Вход B
&
Слайд 581.3.3. Язык логики
1.3. Представление информации
Примеры для самостоятельного решения
1. Для нижеприведенных логических
а)
б)
в)
г)
д)
Слайд 591.3.3. Язык логики
1.3. Представление информации
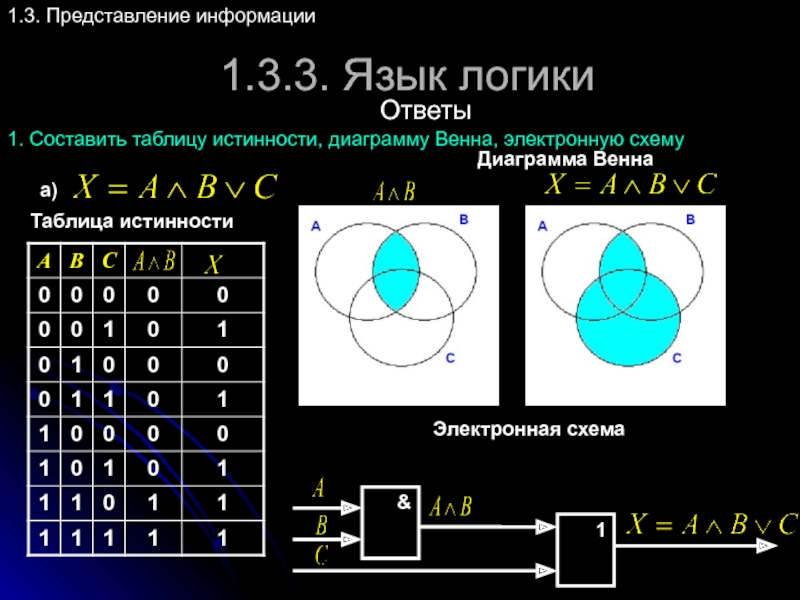
Ответы
1. Составить таблицу истинности, диаграмму Венна, электронную
а)
Таблица истинности
Диаграмма Венна
Электронная схема
&
1
Слайд 601.3.3. Язык логики
1.3. Представление информации
Ответы
1. Составить таблицу истинности, диаграмму Венна, электронную
Таблица истинности
Диаграмма Венна
б)
Слайд 611.3.3. Язык логики
1.3. Представление информации
Ответы
1. Составить таблицу истинности, диаграмму Венна, электронную
&
1
б)
&
1
Электронная схема
Слайд 621.3.3. Язык логики
1.3. Представление информации
Ответы
1. Составить таблицу истинности, диаграмму Венна, электронную
Таблица истинности
в)
Слайд 631.3.3. Язык логики
1.3. Представление информации
Ответы
1. Составить таблицу истинности, диаграмму Венна, электронную
в)
Диаграмма Венна
Слайд 64
1.3.3. Язык логики
1.3. Представление информации
Ответы
1. Составить таблицу истинности, диаграмму Венна, электронную
&
1
1
Электронная схема
в)
1
1
1
Слайд 651.3.3. Язык логики
1.3. Представление информации
Ответы
1. Составить таблицу истинности, диаграмму Венна, электронную
Таблица истинности
г)
Слайд 661.3.3. Язык логики
1.3. Представление информации
Ответы
1. Составить таблицу истинности, диаграмму Венна, электронную
г)
Диаграмма Венна
Слайд 671.3.3. Язык логики
1.3. Представление информации
Ответы
1. Составить таблицу истинности, диаграмму Венна, электронную
&
1
Электронная схема
1
г)
&
&
Слайд 681.3.3. Язык логики
1.3. Представление информации
Ответы
1. Составить таблицу истинности, диаграмму Венна, электронную
Таблица истинности
Диаграмма Венна
Электронная схема
1
&
д)
Слайд 721.3.3. Язык логики
1.3. Представление информации
Примеры для самостоятельного решения
1. Используя аксиомы, свойства
а)
б)
в)
г)
Слайд 731.3.3. Язык логики
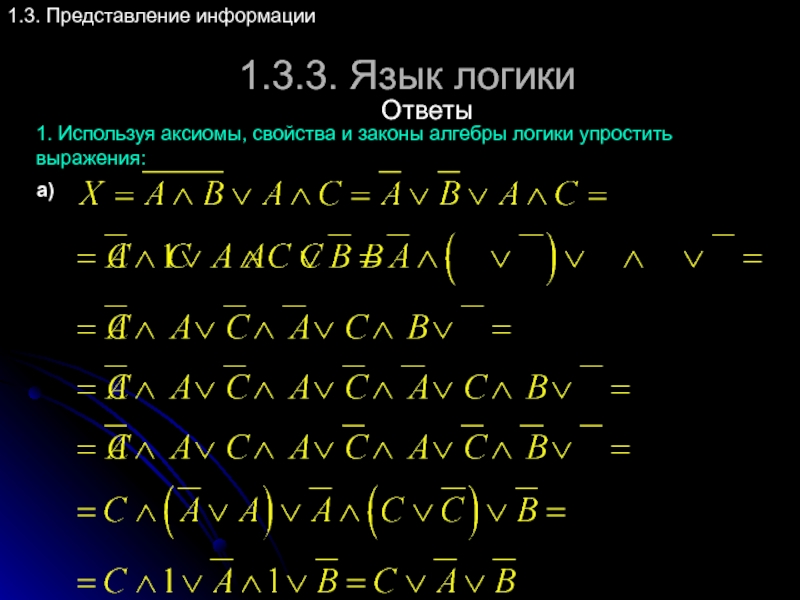
1.3. Представление информации
1. Используя аксиомы, свойства и законы алгебры
а)
Ответы
Слайд 741.3.3. Язык логики
1.3. Представление информации
1. Используя аксиомы, свойства и законы алгебры
б)
Ответы
в)
г)
Слайд 751.3.3. Язык логики
Виды логических электронных схем
1.3. Представление информации
Комбинационные схемы — схемы, выходной
Накапливающие схемы — схемы, выходной сигнал в которых зависит как от входных сигналов, так и от состояния схемы в предыдущие моменты времени.
ЭВМ
Электронные схемы
Комбинированные
Накапливающие
Слайд 761.3.3. Язык логики
Построение логических электронных схем
1.3. Представление информации
Задача: при заданных входных
Ограничение: логическое устройство должно состоять из ограниченного базиса элементов
Критерии оптимальности:
Минимум аппаратуры.
Минимум типов применяемых элементов.
Максимум надежности.
Слайд 771.3.3. Язык логики
Этапы построения логических электронных схем
1.3. Представление информации
Составление математической модели
Анализ логических уравнений и получение минимальной формы для каждой из них в заданном базисе.
Переход от логических уравнений к логической (структурной) схеме посредством применения логических операторов.
Слайд 781.3.3. Язык логики
Обозначения логических функций на электронных схемах
1.3. Представление информации
Слайд 791.3.3. Язык логики
1.3. Представление информации
Примеры для самостоятельного решения
1. Нарисовать электронные схемы
а)
б)
в)
г)
Слайд 801.3.3. Язык логики
1.3. Представление информации
Ответы
1. Нарисовать электронные схемы упрощенных функций на
&
1
а)
&
1
Электронная схема
Электронная схема
1
1
1
Слайд 811.3.3. Язык логики
1.3. Представление информации
Ответы
1. Нарисовать электронные схемы упрощенных функций на
б)
Электронная схема
Электронная схема
&
1
1
1
1
1
1
&
Слайд 821.3.3. Язык логики
1.3. Представление информации
Ответы
1. Нарисовать электронные схемы упрощенных функций на
в)
Электронная схема
Электронная схема
1
&
&
1
1
&
&
Слайд 831.3.3. Язык логики
1.3. Представление информации
Ответы
1. Нарисовать электронные схемы упрощенных функций на
г)
Электронная схема
Электронная схема
1
&
Слайд 841.3.3. Язык логики
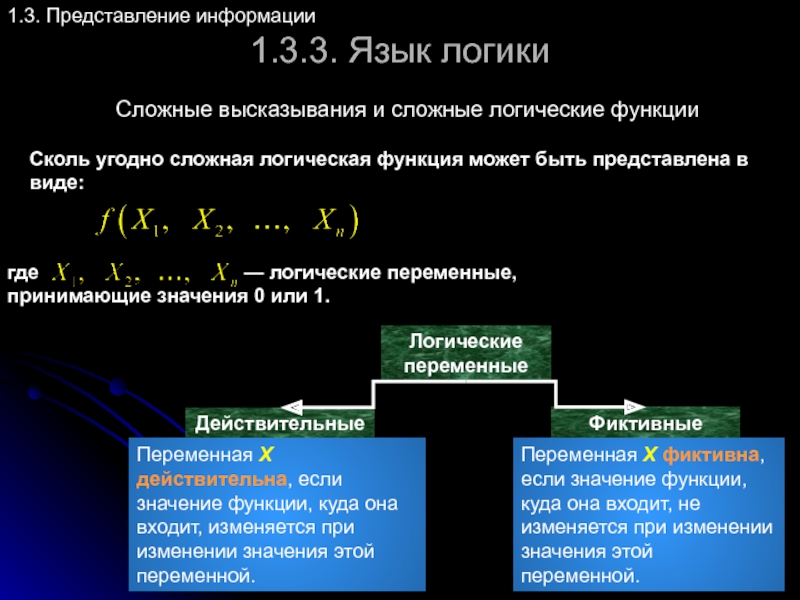
Сложные высказывания и сложные логические функции
1.3. Представление информации
Сколь угодно
где — логические переменные, принимающие значения 0 или 1.
Логические переменные
Действительные
Фиктивные
Переменная X действительна, если значение функции, куда она входит, изменяется при изменении значения этой переменной.
Переменная X фиктивна, если значение функции, куда она входит, не изменяется при изменении значения этой переменной.
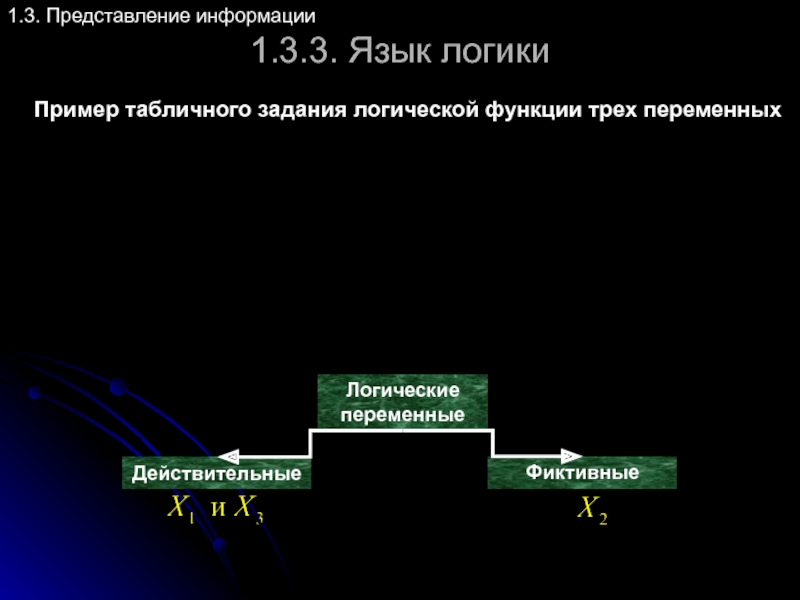
Слайд 851.3.3. Язык логики
Пример табличного задания логической функции трех переменных
1.3. Представление информации
Логические
Действительные
Фиктивные
Слайд 861.3.3. Язык логики
Логический базис
1.3. Представление информации
Булевы функции могут задаваться аналитически, т. е.
Минимальный набор простых логических функций, посредством которого может быть представлена любая функция алгебры логики (ФАЛ), называется логическим базисом или полной системой.
Базис минимален, если удаление хотя бы одной функции превращает систему ФАЛ в неполную.
Минимальные базисы
Базис для практического использования
И, НЕ
ИЛИ, НЕ
И, ИЛИ, НЕ
Слайд 871.3.3. Язык логики
Конъюнктивные и дизъюнктивные термы
1.3. Представление информации
Любая таблично заданная логическая
где — конъюнктивный терм; — дизъюнктивный терм.
Конъюнктивный терм — это логическое произведение переменных и их отрицаний.
Дизъюнктивный терм — это логическая сумма переменных и их отрицаний.
Если терм ФАЛ содержит полный набор переменных, связанных операцией конъюнкции, он носит название минтерм
Термы ФАЛ, состоящие из полного набора переменных, связанных операциями дизъюнкции, называются макстермами
Слайд 881.3.3. Язык логики
Конъюнктивные и дизъюнктивные нормальные формы
1.3. Представление информации
Конъюнктивная нормальная форма
Дизъюнктивная нормальная форма (ДНФ) — это сумма конъюнктивных термов
ДНФ и КНФ, состоящие только из минтерм и макстерм носят названия совершенной дизъюнктивной нормальной формы (СДНФ) и, соответственно, совершенной конъюнктивной нормальной формы (СКНФ).
Слайд 891.3.3. Язык логики
Алгоритм получения СДНФ из таблицы истинности
1.3. Представление информации
1. Выбрать
2. Сформировать из этого набора переменных и их отрицаний минтерм, т. е. произведение переменных или их отрицаний: если переменная набора имеет нулевое значение, то она берется с отрицанием; переменные, имеющие единичные значения в данном наборе не инвертируются.
3. Повторить пункты 1 и 2 для всех других наборов таблицы, где логическая функция равна 1.
4. Построить СДНФ путем логического суммирования полученных минтермов.
Слайд 901.3.3. Язык логики
Алгоритм получения СКНФ из таблицы истинности
1.3. Представление информации
1. Выбрать
2. Сформировать макстерм, т. е. дизъюнктивный набор переменных и их отрицаний: если переменная данного набора равна 0, то она включается в сумму без отрицания, а при равенстве 1 она инвертируется.
3. Повторить пункты 1 и 2 для всех наборов переменных, где значение функции равно 0.
4. Построить СКНФ из полученных дизъюнкций переменных и их отрицаний путем логического умножения.
Слайд 911.3.3. Язык логики
1.3. Представление информации
Примеры для самостоятельного решения
1. Для заданных функций
а)
б)
в)
г)
д)
Слайд 921.3.3. Язык логики
1.3. Представление информации
Ответы
1. Для заданных функций построить СДНФ и
а)
Таблица истинности
СДНФ:
СКНФ:
Слайд 931.3.3. Язык логики
1.3. Представление информации
Ответы
1. Для заданных функций построить СДНФ и
Таблица истинности
СДНФ:
СКНФ:
б)
Слайд 941.3.3. Язык логики
1.3. Представление информации
Ответы
1. Для заданных функций построить СДНФ и
Таблица истинности
СДНФ:
СКНФ:
в)
Слайд 951.3.3. Язык логики
1.3. Представление информации
Ответы
1. Для заданных функций построить СДНФ и
Таблица истинности
СДНФ:
СКНФ:
г)
Слайд 961.3.3. Язык логики
1.3. Представление информации
Ответы
1. Для заданных функций построить СДНФ и
Таблица истинности
СДНФ:
СКНФ:
д)
Слайд 971.3.3. Язык логики
Временные булевы функции
1.3. Представление информации
Временная булева функция (ВБФ) это
, где — количество интервалов автоматного времени.
Любая периодическая временная булева функция может быть представлена в аналитическом виде следующим образом:
где — конъюнктивный терм (или их дизъюнкция) от переменных
; — вспомогательная функция, принимающая значение 1 в момент времени и 0 во всех других случаях.
Если ВБФ зависит еще и от своих предшествующих значений, то она называется рекуррентной булевой функцией (РБФ).