- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Таблицы истинности логических функций презентация
Содержание
- 1. Таблицы истинности логических функций
- 2. Таблицей истинности логической функции принято называть табличное
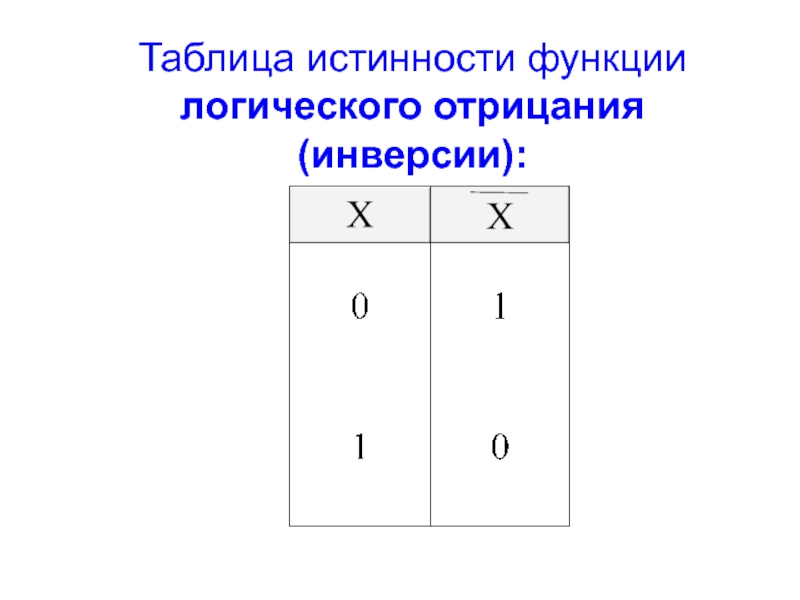
- 3. Таблица истинности функции логического отрицания (инверсии):
- 4. Таблица истинности функции логического сложения (дизъюнкции):
- 5. Свойства дизъюнкции: X ∨ Y ≡ Y
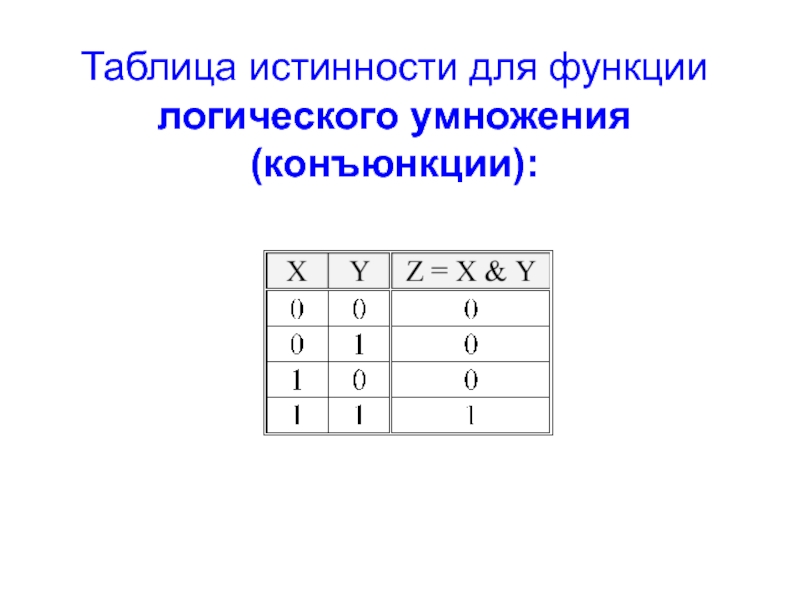
- 6. Таблица истинности для функции логического умножения (конъюнкции):
- 7. Свойства конъюнкции: X & X ≡ X;
- 8. Основные законы алгебры логики
- 11. Правила составления таблиц истинности для сложных логических
- 12. При построении таблиц истинности целесообразно придерживаться следующего
- 13. Затем строится таблица истинности с указанным количеством
- 14. Составление таблицы истинности для логической функции Z
- 15. Построим таблицу, подпишем столбцы и заполним ее
- 16. Теперь выполним необходимые операции и последовательно (слева
Слайд 2Таблицей истинности логической функции принято называть табличное представление логической операции, в котором присутствуют
Слайд 5Свойства дизъюнкции:
X ∨ Y ≡ Y ∨ X;
(X ∨ Y) ∨
X ∨ 0 ≡ X,
где 0 – тождественно ложное высказывание;
X ∨ X ≡ 1;
X ∨ 1 ≡ 1,
где 1 – тождественно истинное высказывание;
X ∨ X ≡ X
Слайд 7Свойства конъюнкции:
X & X ≡ X;
X & Y ≡ Y &
(X & Y) & Z ≡ X & (Y & Z);
X & X ≡ 0;
X & 0 ≡ 0;
где 0 – тождественно ложное высказывание
X & 1 ≡ X,
где 1 – тождественно истинное высказывание
Слайд 11Правила составления таблиц истинности для сложных логических функций
Для любой логической
Слайд 12При построении таблиц истинности целесообразно придерживаться следующего алгоритма действий:
Сначала определяют количество
Далее определяют количество столбцов в таблице истинности, оно равно количеству логических переменных плюс количество логических операций.
Слайд 13Затем строится таблица истинности с указанным количеством строк и столбцов, столбцы
И, наконец, выполняются необходимые логические операции, таблица истинности заполняется по столбцам.
Слайд 14Составление таблицы истинности для логической функции Z = (A ∨ E)
Определим количество строк в нашей таблице истинности.
Мы имеем две логические переменные А и Е, следовательно, количество строк будет равно 22 + 1 = 5.
Выясним, какое количество столбцов необходимо.
У нас – две логические переменные, над которыми будет выполнено 5 логических операций ‑ это A ∨ E, Ā, Ē, Ā ∨ Ē и, наконец (A ∨ E) & (Ā ∨ Ē). Значит, нам понадобится
7 столбцов.
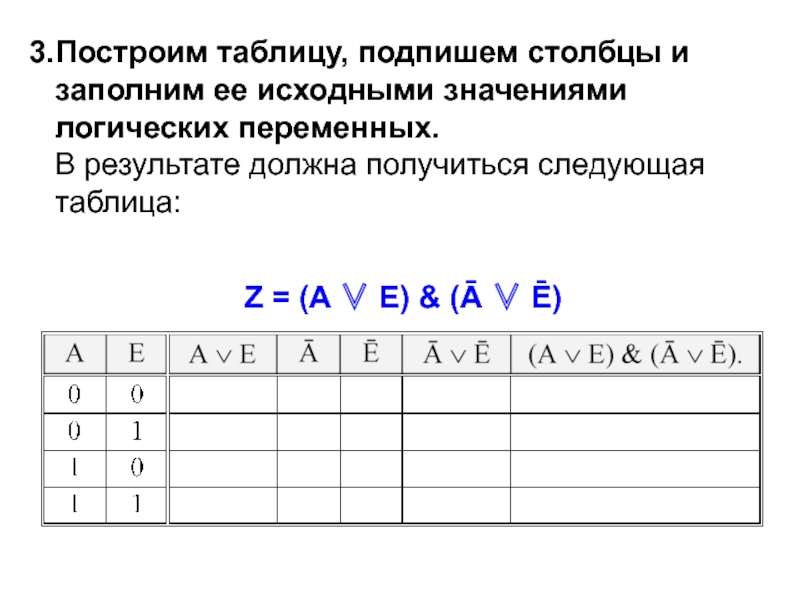
Слайд 15Построим таблицу, подпишем столбцы и заполним ее исходными значениями логических переменных. В
Z = (A ∨ E) & (Ā ∨ Ē)
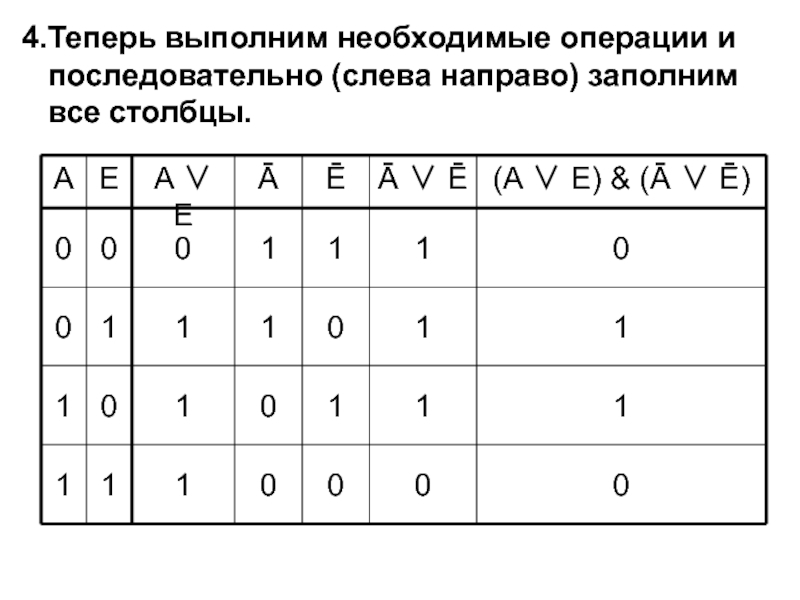
Слайд 16Теперь выполним необходимые операции и последовательно (слева направо) заполним все столбцы.
0
0
0
0
1
1
1
1
1
1
0
1
0
1
1
1
0
1
1
1
0
0
1
1
1
0
0
0
(A
Ā ∨ Ē
Ē
Ā
A ∨ E
E
A