- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Таблицы истинности, функции, логические операции презентация
Содержание
- 1. Таблицы истинности, функции, логические операции
- 2. ТАБЛИЦЫ ИСТИННОСТИ, ФУНКЦИИ На основе логической связи
- 3. ТАБЛИЦЫ ИСТИННОСТИ, ФУНКЦИИ Для выражения логических связей,
- 4. ЛОГИЧЕСКИЕ ОПЕРАЦИИ Проанализируем известные нам логические связи
- 5. ЛОГИЧЕСКИЕ ОПЕРАЦИИ Конъюнкция Возьмём теперь в
- 6. ЛОГИЧЕСКИЕ ОПЕРАЦИИ Дизъюнкция Два высказывания А
- 7. ЛОГИЧЕСКИЕ ОПЕРАЦИИ Неравнозначность Неравнозначность, называемая иногда
- 8. ЛОГИЧЕСКИЕ ОПЕРАЦИИ Импликация Импликация - это
- 9. ЛОГИЧЕСКИЕ ОПЕРАЦИИ Эквивалентность Операция эквивалентность (двойная
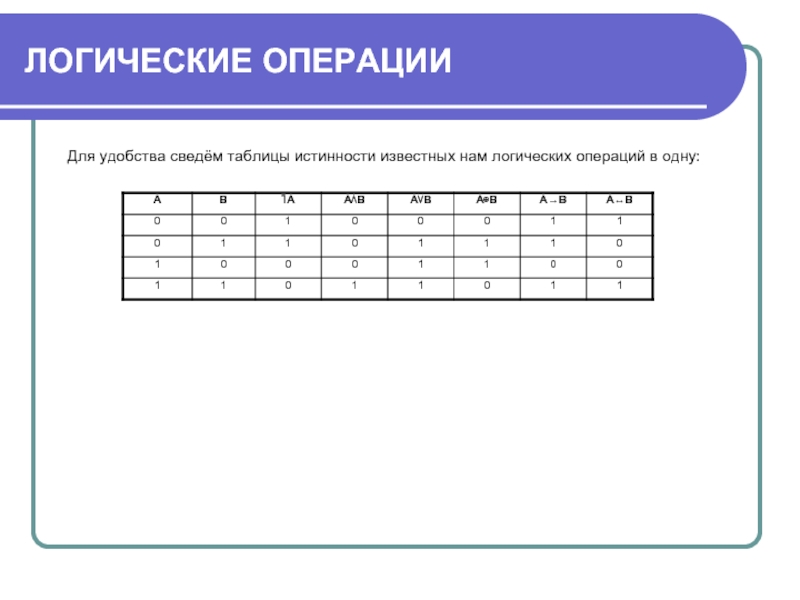
- 10. ЛОГИЧЕСКИЕ ОПЕРАЦИИ Для удобства сведём таблицы истинности известных нам логических операций в одну:
- 11. ФОРМУЛЫ АЛГЕБРЫ ЛОГИКИ Используя основные логические операции,
Слайд 2ТАБЛИЦЫ ИСТИННОСТИ, ФУНКЦИИ
На основе логической связи между простыми высказываниями, входящими в
Пример:
Дано сложное высказывание: “Ученик прогулял урок и получил двойку”.
Здесь связка “и” реализует конъюктивную связь двух высказываний. Составим таблицу истинности:
Логический вывод: анализируя данные таблицы истинности, видим, что сложное высказывание, состоящее из двух простых, истинно, если оба простых истинны.
Слайд 3ТАБЛИЦЫ ИСТИННОСТИ, ФУНКЦИИ
Для выражения логических связей, которые существуют между высказываниями, используется
В алгебре логики сложное высказывание, в котором простые высказывания заменены на логические переменные (значениями переменных могут быть только 0 и 1), логические связки – на математические символы, превращается в логическую функцию.
Пример:
Высказывание “Все мышки и кошки с хвостами” запишется в виде: х1 ∧ х2. Логические переменные х1, х2 связаны между собой конъюктивно. То есть получаем логическую функцию:
F(х1,х2) = х1 ∧ х2
Запишем:
Сложное высказывание является логической (булевой) функцией некоторых двоичных аргументов - простых высказываний, которую можно получить при помощи логических операций.
Основная задача алгебры логики заключается в том, чтобы определить истинность или ложность сложного высказывания на основании истинности или ложности входящих в него простых высказываний.
Таблица соответствия возможных значений аргумента (входных двоичных переменных) значениям функции, называется таблицей истинности.
Количество возможных наборов аргументов равно 2n, где n – число аргументов.
Слайд 4ЛОГИЧЕСКИЕ ОПЕРАЦИИ
Проанализируем известные нам логические связи с учётом вышесказанного, учитывая, что
Простейшие логические операции (И, ИЛИ, НЕ) можно пояснить с помощью диаграмм, предложенных английским логиком Эйлером-Венном.
Инверсия
Первая из этих операций - отрицание некоторого высказывания. Она называется инверсией.
Круг на рисунке обозначает высказывание А, тогда отрицанию этого высказывания соответствует остальная площадь четырёхугольника, т.е. всё, что не относится к А.
Примеры высказываний:
“Неверно, что 2⋅2 = 5”; “Завтра мы не пойдём на улицу”.
В этих примерах отрицание высказываний реализуется связками “неверно, что…” и “не”. Данное высказывание истинно, когда его отрицание ложно и наоборот.
Логическая Функция - F(А) = ⎤А
ТАБЛИЦА ИСТИННОСТИ ОПЕРАЦИИ ОТРИЦАНИЯ:
Логический вывод: инверсия переменной истинна тогда и только тогда, когда переменная ложна.
Слайд 5ЛОГИЧЕСКИЕ ОПЕРАЦИИ
Конъюнкция
Возьмём теперь в качестве высказывания А утверждение "Пасмурно",
Эта логическая операция называется конъюнкцией или логическим И.
На рисунке площадь, принадлежащая обоим кругам, должна соответствовать высказыванию А∧В. Общая для обоих кругов площадь охватывает всё то, что относится одновременно и к А и к В.
Высказывание А∧В “Пасмурно и идёт дождь” может быть истинным лишь тогда, когда истинны оба входящие в него высказывания. Если хотя бы одно из них ложно, то и результат будет ложным.
Логическая функция: F(А,В) = А∧В
ТАБЛИЦА ИСТИННОСТИ ОПЕРАЦИИ КОНЪЮНКЦИЯ:
Логический вывод: конъюнкция логических переменных истинна тогда и только тогда, когда все логические переменные истинны.
Слайд 6ЛОГИЧЕСКИЕ ОПЕРАЦИИ
Дизъюнкция
Два высказывания А и В могут быть связаны словом ИЛИ.
Значение ИЛИ поясняет рисунок. Функция "А или В" изображается площадью, объединяющей оба круга. Заштрихованная область на диаграмме содержит всё то, что принадлежит А и В, причём "и" следует понимать здесь в смысле объединения или суммирования.
Пример высказывания: “В природе бывает, что солнце при дожде светит или прячется в тучах”.
В этом высказывании связка “или” реализует дизъюнкцию, при этом сложное высказывание истинно, если истинно хотя бы одно из простых высказываний, в том числе если истинны сразу оба высказывания.
Логическая функция: F(А,В) = А∨В
ТАБЛИЦА ИСТИННОСТИ ОПЕРАЦИИ ДИЗЪЮНКЦИЯ:
В этих соотношениях находит выражение особенность сложения чисел 1 и 0. Поэтому дизъюнкцию называют иногда также логическим сложением или логической суммой.
Логический вывод: дизъюнкция логических переменных истинна тогда и только тогда, когда истинна хотя бы одна логическая переменная.
Слайд 7ЛОГИЧЕСКИЕ ОПЕРАЦИИ
Неравнозначность
Неравнозначность, называемая иногда исключающее ИЛИ, выражается словосочетанием "или…, или" ("либо…,
Пример высказывания: “В этом году летом мы либо поедем к морю, либо будем жить на даче”.
Связка “либо…либо” реализует строгую дизъюнкцию, при этом сложное высказывание истинно, только если одно из простых высказываний истинно, но не оба сразу.
Логическая функция: F(А,В) = А⊕В
ТАБЛИЦА ИСТИННОСТИ ОПЕРАЦИИ НЕРАВНОЗНАЧНОСТЬ:
Логический вывод: строгая дизъюнкция логических переменных истинна тогда и только тогда, когда истинна хотя бы одна из логических переменных.
Слайд 8ЛОГИЧЕСКИЕ ОПЕРАЦИИ
Импликация
Импликация - это одна из самых важных операций логики высказываний.
Пример высказывания: “Если будет хорошая погода, то мы пойдём в лес”.
Здесь связка “если…то” реализует импликацию, при этом первую часть высказывания – “Если будет хорошая погода” – называют основанием, а вторую – “мы пойдём в лес” – следствием.
Высказывание такого типа ложно только в одном случае – если истинно условие и ложно заключение.
Логическая функция: F(А,В) = А→В
ТАБЛИЦА ИСТИННОСТИ ОПЕРАЦИИ ИМПЛИКАЦИЯ:
Логический вывод: импликация двух логических переменных ложна тогда и только тогда, когда условие истинно, а заключение ложно.
Слайд 9ЛОГИЧЕСКИЕ ОПЕРАЦИИ
Эквивалентность
Операция эквивалентность (двойная импликация) обозначается знаками ↔, ≡.
Пример высказывания:
В этом примере связка “…тогда и только тогда…когда…” помогает выразить взаимную обусловленность событий. Данное сложное высказывание будет истинным, когда простые высказывания либо оба истинны, либо оба ложны.
Логическая функция: F(А,В) = А↔В
ТАБЛИЦА ИСТИННОСТИ ОПЕРАЦИИ ЭКВИВАЛЕНТНОСТЬ:
Логический вывод: эквивалентность двух логических переменных истинна тогда и только тогда, когда обе переменные одновременно истинны или одновременно ложны.
Слайд 10ЛОГИЧЕСКИЕ ОПЕРАЦИИ
Для удобства сведём таблицы истинности известных нам логических операций в
Слайд 11ФОРМУЛЫ АЛГЕБРЫ ЛОГИКИ
Используя основные логические операции, можно построить более сложные высказывания,
(А∧В) ∨ (А∧В) ∨ (А∧С),
(А∨⎤А) ∧ (В→АС),
(⎤(А∨В) → С).
Указанные высказывания называются формулами алгебры высказываний. Эти формулы состоят из простых высказываний А, В, …, знаков логических операций и скобок.
ПОСЛЕДОВАТЕЛЬНОСТЬ ВЫПОЛНЕНИЯ ОПЕРАЦИЙ
Скобки указывают последовательность выполнения операций. При отсутствии скобок первой всегда выполняется операция отрицания, затем конъюнкция (логическое произведение), дизъюнкция (логическое сложение) и неравнозначность, затем импликация и эквивалентность:
⌉;
∧;
+ , ⊕;
→, ↔.
Пример. Какие из приведённых ниже выражений являются формулами логики высказываний, а какие нет?
А + → В;
(+ p + q);
p → q → r;
(p + q) → r.