- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сучасні комп’ютерні технології в економічній науці та практиці презентация
Содержание
- 1. Сучасні комп’ютерні технології в економічній науці та практиці
- 2. Тема: Інформаційні технології імовірнісного та статистичного моделювання
- 3. 1. Генерація випадкових величин Генерація випадкових величин,
- 4. Приклади генерації випадкових величин
- 5. Генерація випадкових чисел, розподілених за різними законами
- 6. Для включення інструменту Генерация случайных чисел слід
- 7. 2. Розрахунок числових характеристик розподілу ймовірностей
- 8. Розрахунок числових характеристик дискретних випадкових величин, закон
- 9. Приклад: Щоденні витрати на обслуговування і рекламу
- 11. Розрахунок числових характеристик біноміального розподілу Біноміальний розподіл
- 12. Приклад: Банк видає 5 кредитів. Ймовірність неповернення
- 13. Розрахунок числових характеристик нормального закону розподілу В
- 14. Рішення
- 15. 3. Рішення задач статистичного аналізу в Excel
- 16. Приклад: Побудувати емпіричний розподіл рейтингу студентів за
- 17. Рішення із використанням інструменту “Гистограмма”: Вибіркова функція розподілу має вид:
- 18. Обчислення основних статистичних характеристик через використання вбудованих
- 19. Функції Excel, що характеризують розсіювання Функція
- 20. Приклад: В таблиці наведені відомості про щомісячну
- 21. Обчислення основних статистичних характеристик із використанням вбудованих
- 22. Рішення:
- 23. Перевірка статистичних гіпотез в Excel Обчислення довірчого
- 24. Рішення із використанням функції ДОВЕРИТ Тут альфа
- 25. Рішення за допомогою інструменту “Описательная статистика” В
- 26. Перевірка відповідності теоретичного розподілу із використанням критерію
- 27. Рішення {=ЧАСТОТА(A2:A52;F2:F11)} {=G2:G12/G13} {=НОРМРАСП(F2:F12;H15;H16;0)} =J2*F2 =K2*$G$13/СУММ($K$2:$K$12)
- 28. 4. Рішення задач дисперсійного аналізу в Excel
- 29. Рішення: У результуючій таблиці на перетині рядка
- 30. 5. Рішення задач кореляційного аналізу в Excel
- 31. Рішення: У трикутній матриці коефіцієнт кореляції між
- 32. 6. Технології рішення задач регресійного аналізу в
- 33. Приклад: Існують статистичні дані про витрати, пов’язані
- 34. 1. Коефіцієнт детермінізації R-квадрат = 0,974 (апроксимація
- 35. Оптимізація портфеля цінних паперів в Excel Відомо,
- 36. Технологічна послідовність комп’ютерного рішення задачі Економіко-статистичний
- 38. Математична модель інвестора Знайти Х = (Х1,
- 39. Складання комп’ютерного аналога математичної моделі за допомогою
- 40. 7. Технології рішення задач фінансової математики в
- 41. Розрахунок за простими змінними ставками За час
- 42. Розрахунок реінвестування за простими процентами Сума із
- 43. Дисконтування в Excel Операція дисконтування полягає у
- 44. Обчислення нарощування за складними процентами в Excel
- 45. Обчислення нарощеної суми при змінній процентній ставці
Слайд 1Сучасні комп’ютерні технології в економічній науці та практиці
Доц. Кривенко В.І.
Кафедра електроніки
Слайд 2Тема: Інформаційні технології імовірнісного та статистичного моделювання економічних процесів
Питання
Генерація випадкових величин
Розрахунок
Рішення задач статистичного аналізу в табличному процесорі Excel
Технологія рішення задач дисперсійного аналізу
Рішення задач кореляційного аналізу
Технологія рішення задач регресійного аналізу
Технологія рішення задач фінансової математики в табличному процесорі Excel
Слайд 31. Генерація випадкових величин
Генерація випадкових величин, розподілених за рівномірним законом
Дискретний рівномірний
В Excel випадкову величину, що розподілена за рівномірним законом, генерує функція СЛЧИС(), яка відноситься до категорії Математичні. Функція видає випадкове дійсне число у діапазоні 0÷1.
Для іншого діапазону слід застосувати формулу:
= СЛЧИС()*(b–a)+a, де a і b – відповідно задані нижня і верхня межа діапазону.
Для генерації цілої випадкової величини, що має рівномірний розподіл у діапазоні між двома заданими числами в Excel у категорії Математичні є функція СЛУЧМЕЖДУ(Нижня_межа; Верхня_межа)
Слайд 5Генерація випадкових чисел, розподілених за різними законами
Для генерації випадкових чисел розподілених
1. Рівномірний розподіл характеризується верхньою та нижньою межами.
Ймовірність попадання змінної у відрізок фіксованої довжини залежить тільки від довжини відрізка і не залежить від його розташування на інтервалі. Як правило, в додатках використовують рівномірний розподіл в інтервалі [0,1].
2. Нормальний розподіл характеризується середнім значенням і стандартним відхиленням.
Зазвичай програми для цього розподілу використовують середнє значення 0 і стандартне відхилення 1.
3. Розподіл Бернуллі характеризується ймовірністю успіху в даному випробуванні.
Випадкова величина приймає значення 0 або 1.Наприклад, при киданні гральної кістки або випаде 6 очок з імовірністю 1 / 6 або випаде не 6 очок з імовірністю 5 / 6, тобто випадкова величина приймає значення 1 з ймовірністю 1 / 6 або 0 з імовірністю 5 / 6.
4. Біноміальний розподіл характеризується ймовірністю успіху для деякого числа випробувань.
Наприклад, можна генерувати випадкові числа, що моделюють процес кидання монети з імовірністю успіху у "k" випадків з "n" випробувань.
5. Розподіл Пуассона характеризується значенням Лямбда, рівним 1/середнє.
Розподіл Пуассона часто використовується для характеристики числа подій, що трапляються в одиницю часу, наприклад, число телефонних з'єднань в хвилину.
6. Модельний розподіл характеризується нижньою і верхньою границею, кроком, числом повторень значень і числом повторень послідовності.
7. Дискретний розподіл характеризується значенням і пов'язаним з ним інтервалом вірогідності.
Інтервал повинен містити два стовпці: лівий містить значення, правий - ймовірно, пов'язані зі значенням в цьому рядку. Сума ймовірностей повинна дорівнювати 1.
Слайд 6Для включення інструменту Генерация случайных чисел слід виконати команду:
Якщо інструмент недоступний,
в Excel 1997-2003: Сервис → Надстройки → прапорець Пакет анализа → ОК;
В Excel 2007 і пізніших: кнопка Office → кнопка Параметры Excel → Надстройки → кнопка Перейти → прапорець Пакет анализа → ОК.
в Excel 1997-2003: Сервис → Пакет анализа → Генерация случайных чисел;
в Excel 2007 і пізніших: стрічка Данные → панель Анализ → Анализ данных → Генерация случайных чисел
Слайд 72. Розрахунок числових характеристик розподілу ймовірностей
Числовими характеристиками розподілу ймовірностей випадкових величин,
Першим моментом випадкової величини є математичне очікування або середнє значення, яке характеризує центр розподілу ймовірностей.
Другим моментом, що характеризує розкид випадкової величини відносно математичного очікування є центральний момент випадкової величини, який називається дисперсією. Величина, що дорівнює кореню квадратному із дисперсії називається середньоквадратичним відхиленням.
Для випадкових дійсних величин застосовують такі характеристики, як квантѝлі. Квантилью Хρ випадкової величини, що має функцію розподілу F(x) називається рішення Хρ рівняння F(x) = ρ, де ρ – задана ймовірність. Серед квантилей частіше використовують медіану і квáртилі розподілу.
Медіаною називають квантиль, що відповідає значенню ρ = 0,5.
Верхньою квартилью називається квантиль, що відповідає значенню ρ = 0,75, а нижньою – квантиль, що відповідає значенню ρ = 0,25.
В Excel для обчислення деяких числових характеристик дискретних розподілів ймовірностей застосовуються функції СРЗНАЧ, ДИСПР, СТАНДОТКЛОНП, КВАРТИЛЬ і ПЕРСЕНТИЛЬ із категорії СТАТИСТИЧЕСКИЕ
Слайд 8Розрахунок числових характеристик дискретних випадкових величин, закон розподілу яких заданий таблицею
Відповідність між окремими можливими значеннями випадкової величини і їх ймовірностями називається законом розподілу дискретної випадкової величини.
Закон розподілу дискретної випадкової величини може бути заданий таблицею:
При розподілі, що заданий таблицею, математичне очікування розраховується за формулою:
М(X) = х1p1 + х2p2 + … + хnpn.
Дисперсія дискретної випадкової величини визначається за формулою:
D(X) = M(X2) – [M(X)]2.
Середньоквадратичне відхилення дискретної випадкової величини визначається за формулою:
σ(X) =
Слайд 9Приклад:
Щоденні витрати на обслуговування і рекламу автомобілів у автосалоні складає у
Вирахувати математичне очікування щоденного прибутку при ціні автомобіля 150 тис. грош. Од. (281,25 тис. грош. од.)
Рішення:
Прибуток визначається виразом: П = Кількість_продаж * Ціна – Витрати
Для розрахунку необхідно визначити математичне очікування кількості автомобілів, що продаються за день
Слайд 11Розрахунок числових характеристик біноміального розподілу
Біноміальний розподіл – один із розповсюджених дискретних
Для визначення ймовірності окремого значення біноміального розподілу або значення випадкової величини за заданою ймовірністю в Excel є функції БИНОМРАСП та КРИТБИНОМ (категорія Статистичні).
Функція БИНОМРАСП застосовується для вирахування ймовірності в задачах із фіксованим числом випробувань, коли результат будь-якого випробування може мати одне із двох значень – успіх або невдача.
Функція КРИТБИНОМ застосовується для вирахування найменшого числа успішних результатів випадкової величини, для якого інтегральний біноміальний розподіл більше або дорівнює заданій величині (критерію).
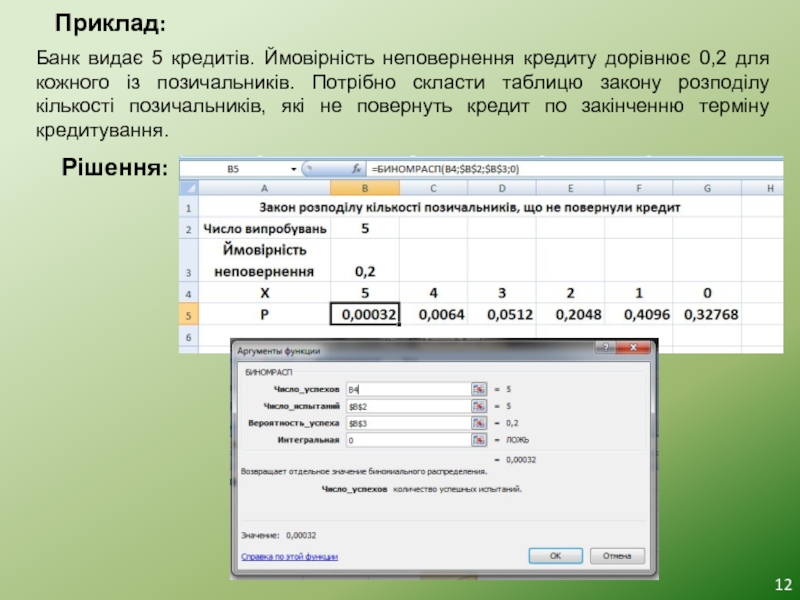
Слайд 12Приклад:
Банк видає 5 кредитів. Ймовірність неповернення кредиту дорівнює 0,2 для кожного
Рішення:
Слайд 13Розрахунок числових характеристик нормального закону розподілу
В Excel для розрахунку значень характеристик
Функція НОРМРАСП розраховує значення ймовірності нормальної функції розподілу для заданого середнього і стандартного відхилення.
Функція НОРМОБР розраховує квантилі для вказаного середнього і стандартного відхилення (розв’язує рівняння F(x) = ρ).
Функція НОРМАЛИЗАЦИЯ за заданим значення х і параметрам розподілу розраховує нормальне значення, що відповідає х.
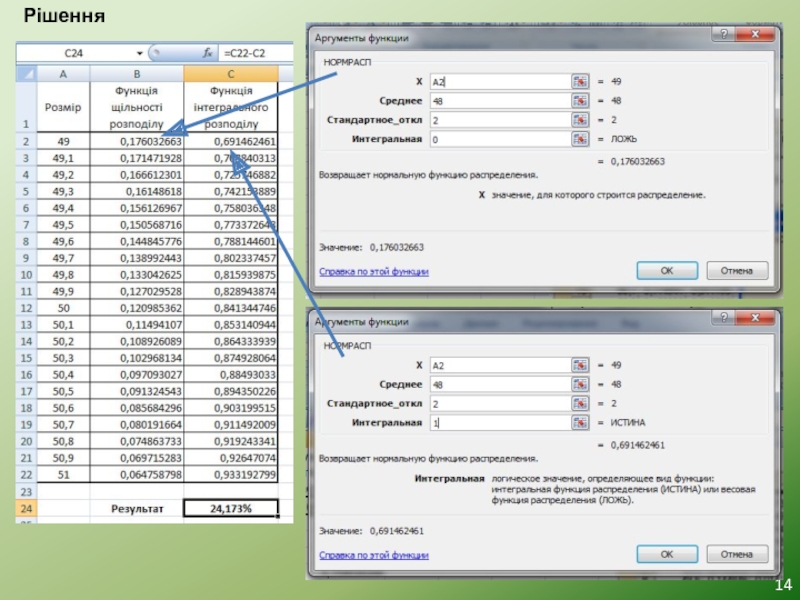
Приклад:
Магазин продає чоловічі костюми. Розподіл попиту за розмірами є нормальним із математичним очікуванням М = 48 і σ(стандартне відхилення) = 2. Необхідно розрахувати процент попиту на 50 розмір костюму за умови розкиду значень цієї величини в інтервалі (49,51).
Слайд 153. Рішення задач статистичного аналізу в Excel
Побудова вибіркової функції розподілу
На практиці
Вся сукупність об’єктів, із якої здійснюється вибірка, називається генеральною сукупністю. Сукупність випадково відібраних із генеральної сукупності об’єктів називається вибірковою сукупністю.
В Excel для побудови вибіркової функції розподілу використовується спеціальна функція ЧАСТОТА (категорія Статистичні) і інструмент із Пакету аналізу Гистограмма.
Функція ЧАСТОТА вираховує частоти появи випадкових величин в інтервалі значень і видає їх масивом чисел. Параметри функції: ЧАСТОТА(масив_даних; масив_інтевалів). Функція повинна задаватись як формула масиву: після виділення діапазону результатів вводиться формула і натискаються клавіші Ctrl+Chift+Enter.
Інструмент Гистограмма слугує для розрахунку вибіркових і інтегральних частот попадання даних у вказані інтервали значень. Результатом є таблиця і гістограма.
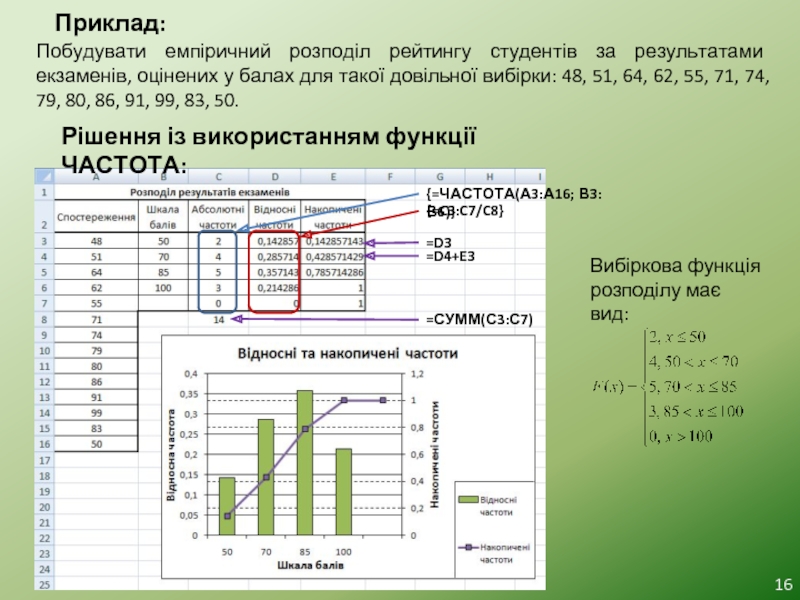
Слайд 16Приклад:
Побудувати емпіричний розподіл рейтингу студентів за результатами екзаменів, оцінених у балах
Рішення із використанням функції ЧАСТОТА:
{=ЧАСТОТА(А3:А16; В3:В6)}
{=C3:C7/C8}
=D4+E3
=D3
=СУММ(С3:С7)
Вибіркова функція розподілу має вид:
Слайд 18Обчислення основних статистичних характеристик через використання вбудованих функцій Excel
Функція СРЗНАЧ
Функція СРГАРМ обчислює середнє гармонічне множини чисел. Середнє гармонічне – величина зворотна до середнього арифметичного зворотних величин;
Функція СРГЕОМ обчислює середнє геометричне значень масиву додатних чисел. Цю функцію можна використовувати для обчислення середніх показників динамічного ряду;
Функція МЕДИАНА дозволяє визначити медіану заданої вибірки. Медіана – це елемент вибірки, число елементів із значенням більше якого і менше якого рівні. Наприклад, МЕДИАНА(5; 6; 8; 5; 9; 10; 8; 9) дорівнює 8;
Функція МОДА визначає елемент вибірки, який найчастіше зустрічається у вибірці (найбільш ймовірна величина).
Слайд 19Функції Excel, що характеризують розсіювання
Функція ДИСП дозволяє оцінити дисперсію за
Функція СТАНДОТКЛОН обчислює стандартне відхилення – характеризує степінь розкиду елементів вибірки відносно середнього значення;
Функція ПЕРСЕНТИЛЬ дозволяє обчислити квантилі заданої вибірки.
Функції Excel, що дозволяють оцінити форму емпіричного розподілу
Функція ЭКССЦЕСС – обчислює оцінку ексцесу за вибірковими даними – степінь виразності хвостів розподілу, тобто частоти появи значень вибірки віддалених від середнього значення;
Функція СКОС дозволяє оцінити асиметрію вибіркового розподілу – величину, що характеризує несиметричність розподілу елементів вибірки відносно середнього значення.
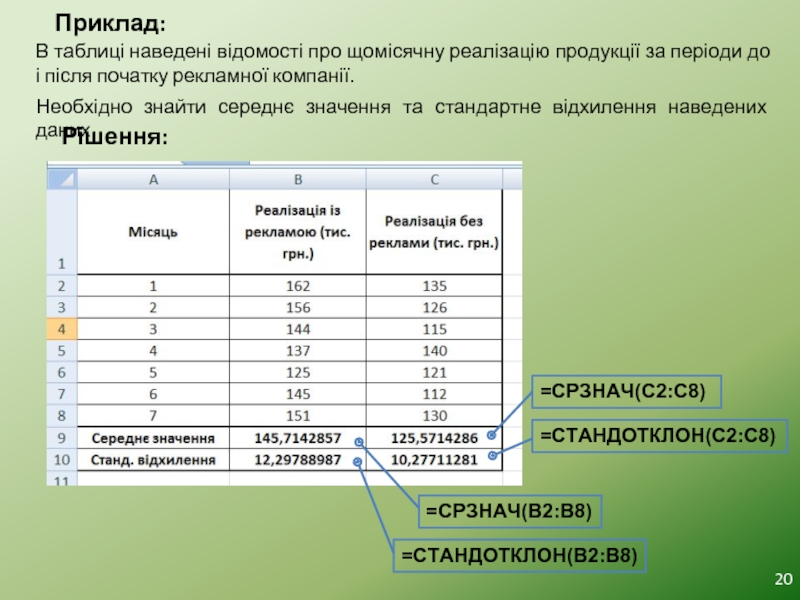
Слайд 20Приклад:
В таблиці наведені відомості про щомісячну реалізацію продукції за періоди до
Необхідно знайти середнє значення та стандартне відхилення наведених даних.
Рішення:
=СРЗНАЧ(B2:B8)
=СРЗНАЧ(C2:C8)
=СТАНДОТКЛОН(B2:B8)
=СТАНДОТКЛОН(C2:C8)
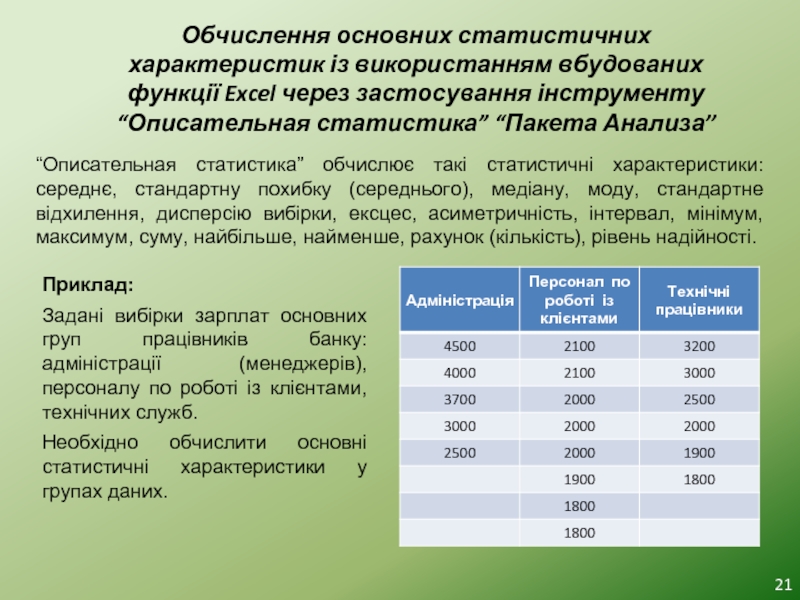
Слайд 21Обчислення основних статистичних характеристик із використанням вбудованих функції Excel через застосування
“Описательная статистика” обчислює такі статистичні характеристики: середнє, стандартну похибку (середнього), медіану, моду, стандартне відхилення, дисперсію вибірки, ексцес, асиметричність, інтервал, мінімум, максимум, суму, найбільше, найменше, рахунок (кількість), рівень надійності.
Приклад:
Задані вибірки зарплат основних груп працівників банку: адміністрації (менеджерів), персоналу по роботі із клієнтами, технічних служб.
Необхідно обчислити основні статистичні характеристики у групах даних.
Слайд 23Перевірка статистичних гіпотез в Excel
Обчислення довірчого інтервалу для середнього значення
Для обчислення
ДОВЕРИТ(альфа; станд_відхил; розмір), де параметри:
альфа – рівень значимості, який використовується для обчислення довірчої ймовірності;
станд_відхил – стандартне відхилення генеральної сукупності для інтервалу даних (передбачається відомим або попередньо розраховується);
розмір – розмір вибірки.
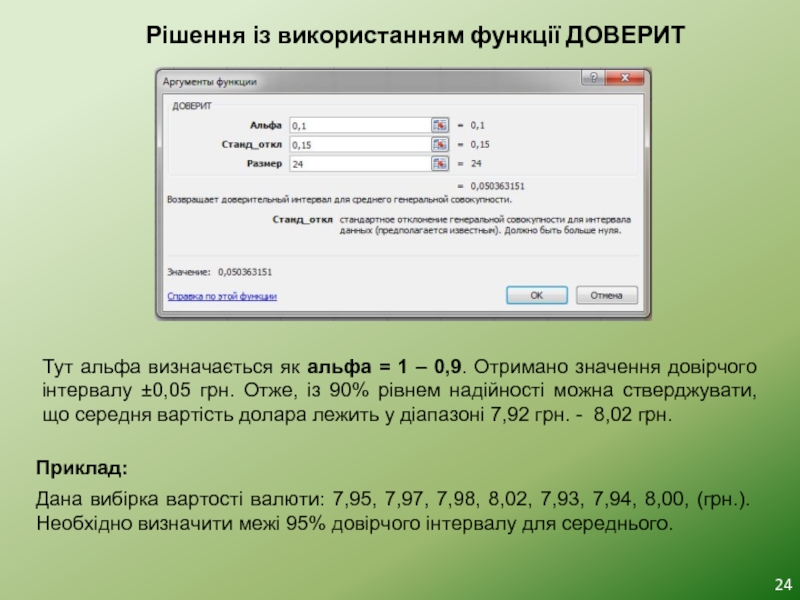
Приклад:
Знайти межі 90% інтервалу для середнього значення, якщо за результатами 24 торгів середнє значення вартості долара склало 7,97 гривні, а стандартне відхилення – 25 копійок.
Слайд 24Рішення із використанням функції ДОВЕРИТ
Тут альфа визначається як альфа = 1
Приклад:
Дана вибірка вартості валюти: 7,95, 7,97, 7,98, 8,02, 7,93, 7,94, 8,00, (грн.). Необхідно визначити межі 95% довірчого інтервалу для середнього.
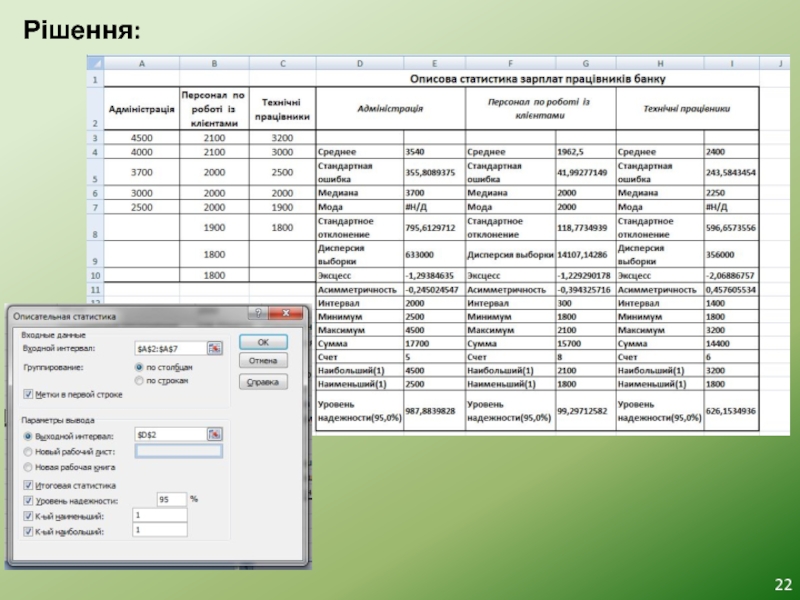
Слайд 25Рішення за допомогою інструменту “Описательная статистика”
В результаті обчислень для довірчої ймовірності
Слайд 26Перевірка відповідності теоретичного розподілу із використанням критерію згоди хі-квадрат
В MS Excel
ХИ2ТЕСТ (фактичний_інтервал; очікуваний_інтервал), де
фактичний_інтервал - діапазон даних, який містить результати спостереження, що підлягають порівнянню з очікуваними значеннями;
очікуваний_інтервал - діапазон даних, який містить теоретичні (очікувані) значення для відповідних спостережуваних.
Для отримання правильних результатів необхідно, щоб обсяг вибірки був не менше 40. Дані згруповані в інтервальний ряд з кількістю інтервалів не менше 7, а кількість спостережень у кожному інтервалі (частот) не менше 5.
Приклад.
Перевірити відповідність вибіркових даних результатів здачі іспитів, оцінених у балах: 48, 51,67, 70, 64, 71, 85, 79, 80, 83, 86, 91, 99, 56, 66, 65, 84, 84, 84, 75, 76, 77, 78, 80, 86, 88, 58, 69, 65, 81, 75, 78, 85, 80, 80, 83, 86, 80, 89, 60, 68, 55, 82, 64.71, 72, 72, 73, 74, 74, 79 нормальному закону розподілу.
Слайд 27Рішення
{=ЧАСТОТА(A2:A52;F2:F11)}
{=G2:G12/G13}
{=НОРМРАСП(F2:F12;H15;H16;0)}
=J2*F2
=K2*$G$13/СУММ($K$2:$K$12)
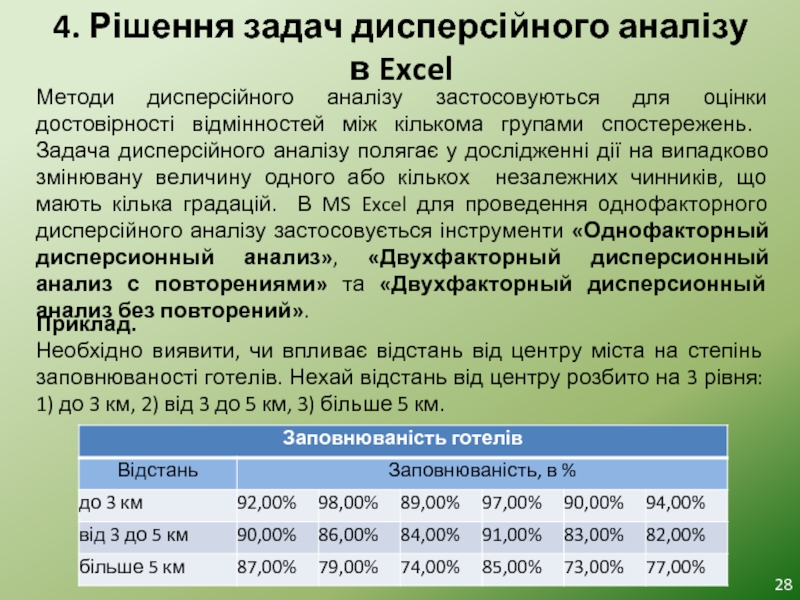
Слайд 284. Рішення задач дисперсійного аналізу в Excel
Методи дисперсійного аналізу застосовуються для
Приклад.
Необхідно виявити, чи впливає відстань від центру міста на степінь заповнюваності готелів. Нехай відстань від центру розбито на 3 рівня: 1) до 3 км, 2) від 3 до 5 км, 3) більше 5 км.
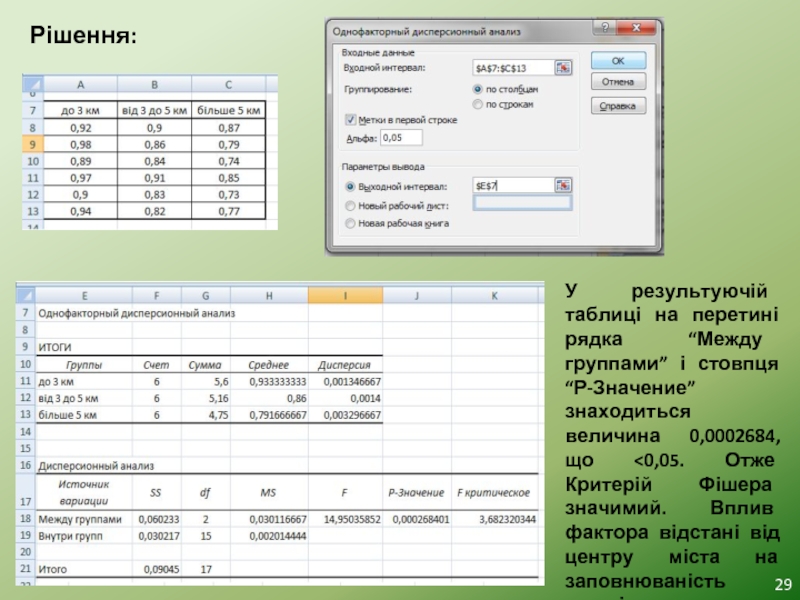
Слайд 29Рішення:
У результуючій таблиці на перетині рядка “Между группами” і стовпця “Р-Значение”
Слайд 305. Рішення задач кореляційного аналізу в Excel
Однією із задач статистики є
Задача подібного дослідження розв’язується методами кореляційного аналізу.
Метою рішення задачі є отримання кореляційної матриці
У MS Excel для здійснення кореляційного аналізу слугує інструмент Корреляция, який дозволяє отримати кореляційну матрицю, що містить коефіцієнти кореляції між різними параметрами.
Кореляційна матриця – це квадратна таблиця, на перетині відповідних рядків і стовпців розташовані кореляційні коефіцієнти.
Приклад:
Є статистичні дані, що реєструють кількість вихідних і святкових днів у місяці в період із січня по червень і суми коштів, що знімаються з рахунків.
Необхідно визначити, чи існує кореляція між кількістю вихідних днів і сумами, що знімаються з рахунків.
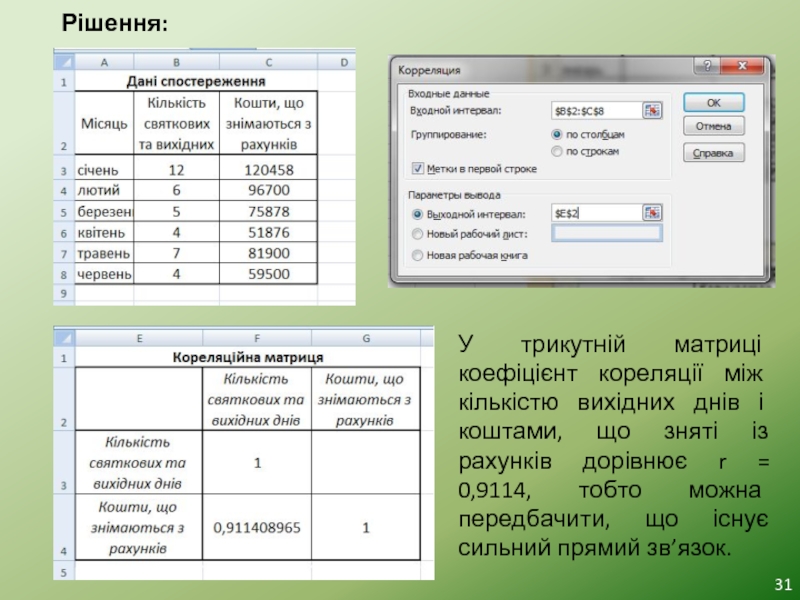
Слайд 31Рішення:
У трикутній матриці коефіцієнт кореляції між кількістю вихідних днів і коштами,
Слайд 326. Технології рішення задач регресійного аналізу в Excel
Регресія дозволяє проаналізувати дію
Якщо розглядати залежність між однією залежною змінною Y і кількома незалежними Х1, Х2, … , Хn , то мова йде про множинну лінійну регресію. В цьому випадку рівняння регресії має вид:
Y= а0 + а1 Х1 + а2 Х2 + … + аn Хn ,
де а1, а2, …, аn - коефіцієнти при незалежних змінних, які необхідно розрахувати (коефіцієнти регресії), а0 – константа.
При побудові регресійної моделі найважливішим моментом є оцінка її адекватності (ефективності) і значимості, на основі яких можна судити про можливість застосування в практиці отриманої моделі.
Мірою оцінки адекватності регресійної моделі є коефіцієнт детермінації R2 (R-квадрат), який визначає , з якою степені точності отримане рівняння регресії апроксимує вихідні дані.
Значимість регресійної моделі оцінюється за допомогою критерію Фішера (F-критерію). Якщо величина F-критерію значима (р < 0,05), то регресійна модель є значимою.
У MS Excel для обчислення коефіцієнтів регресії слугує інструмент “Регрессия” із Пакету аналізу. Він дозволяє отримувати коефіцієнти рівняння лінійної регресії , що може включати до 16 незалежних змінних.
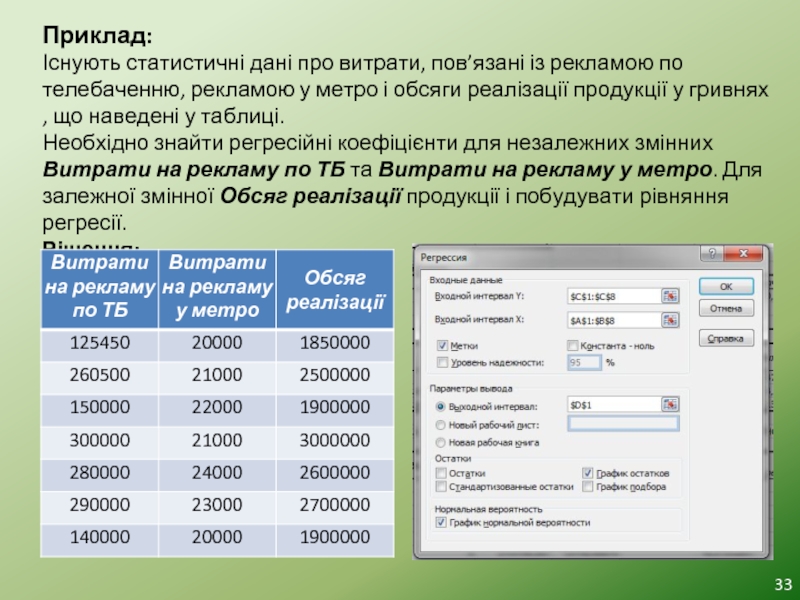
Слайд 33Приклад:
Існують статистичні дані про витрати, пов’язані із рекламою по телебаченню, рекламою
Необхідно знайти регресійні коефіцієнти для незалежних змінних Витрати на рекламу по ТБ та Витрати на рекламу у метро. Для залежної змінної Обсяг реалізації продукції і побудувати рівняння регресії.
Рішення:
Слайд 341. Коефіцієнт детермінізації R-квадрат = 0,974 (апроксимація задовільна).
2. Значимість F =
3. Y-пересечение а0 = 2106723,34.
4. а1 = 6,395 – коефіцієнт при незалежній змінній X1 - Витрати на рекламу по ТБ.
5. а2 = -54,194 – коефіцієнт при незалежній змінній X2 - Витрати на рекламу у метро.
З урахуванням отриманих даних рівняння регресії матиме вид: Y = 2106723,34 + 6,395X1 – 54,194X2.
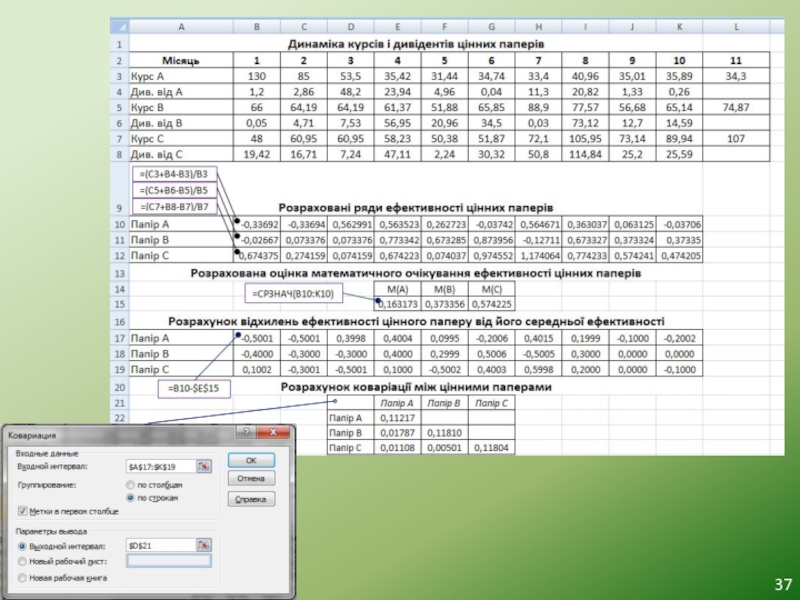
Слайд 35Оптимізація портфеля цінних паперів в Excel
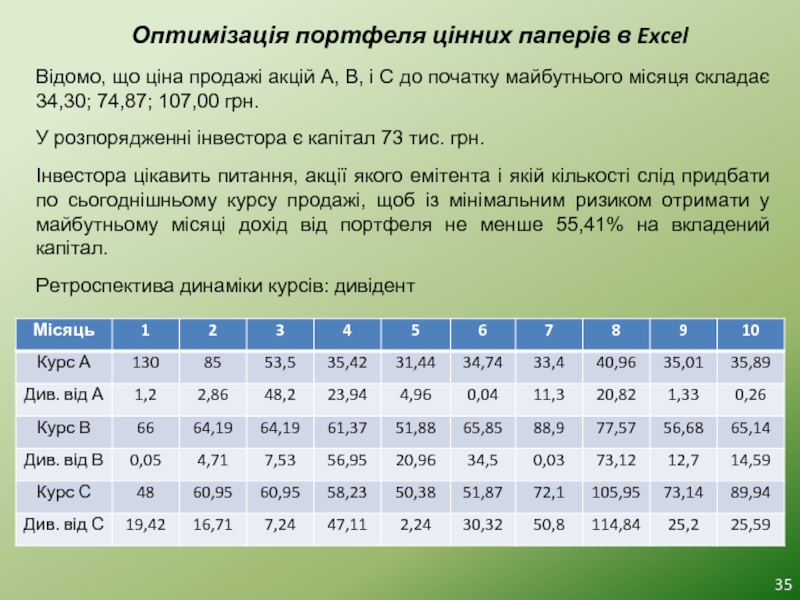
Відомо, що ціна продажі акцій А,
У розпорядженні інвестора є капітал 73 тис. грн.
Інвестора цікавить питання, акції якого емітента і якій кількості слід придбати по сьогоднішньому курсу продажі, щоб із мінімальним ризиком отримати у майбутньому місяці дохід від портфеля не менше 55,41% на вкладений капітал.
Ретроспектива динаміки курсів: дивідент
Слайд 36Технологічна послідовність комп’ютерного рішення задачі
Економіко-статистичний аналіз даних.
Введення даних на робочий листок
Розрахунок рядів ефективності цінних паперів (ЦП).
Розрахунок середньої ефективності по кожному ЦП.
Розрахунок відхилень ефективності кожного ЦП від свого середнього.
Розрахунок коваріації.
Побудова математичної моделі оптимізації портфеля цінних паперів.
Формалізація математичної моделі на робочому листку Excel.
Складання комп’ютерного аналога математичної моделі за допомогою інструменту (надбудови) “Поиск решения” і виконання розрахунків.
Економічна інтерпретація результатів.
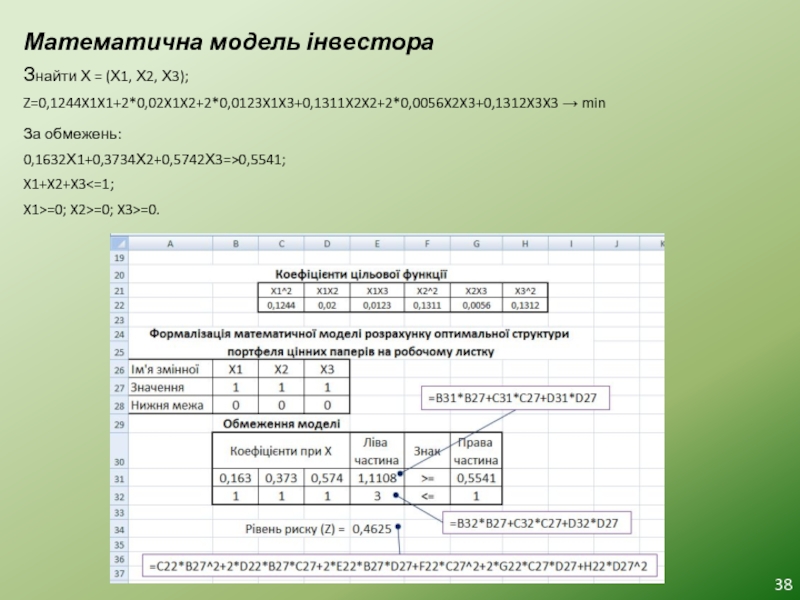
Слайд 38Математична модель інвестора
Знайти Х = (Х1, Х2, Х3);
Z=0,1244X1X1+2*0,02X1X2+2*0,0123X1X3+0,1311X2X2+2*0,0056X2X3+0,1312X3X3 → min
За обмежень:
0,1632Х1+0,3734Х2+0,5742Х3=>0,5541;
X1+X2+X3=0;
Слайд 39Складання комп’ютерного аналога математичної моделі за допомогою інструменту (надбудови) “Поиск решения”
Висновок: інвестору слід вкласти 10% капіталу в акції емітента В і 90% капіталу – в акції емітента С.
Слайд 407. Технології рішення задач фінансової математики в Excel
Розрахунок нарощеної суми за
Під нарощеною сумою позики (депозиту, боргу) розуміють її початкова сума плюс нараховані на неї до кінця терміну відсотки. Нарощена сума розраховується як останній елемент прогресії, що має загальний член P(1 + ni), тобто
S = P(1 + ni),
де Р – початкова сума;
n – кількість періодів;
і – ставка за період.
Розрахунок кількості днів в періоді, який заданий початковою і кінцевою датами
Для розрахунку кількості днів між двома датами в Excel є функція:
ДНЕЙ360(Початкова_дата; Кінцева_дата; Метод)
Слайд 41Розрахунок за простими змінними ставками
За час розрахункового періоду ставки можуть дискретно
де Р – початкова сума; it – ставка простих процентів в період з номером t = 1, …, m; nt – тривалість t періоду нарахування за ставкою it.
Приклад:
У договорі, розрахованим на рік, прийнята ставка простих процентів на перший квартал у розмірі 8% річних, а на кожний наступний на 0,5% менше ніж у попередній. Визначити суму на рахунку у кінці року.
Слайд 42Розрахунок реінвестування за простими процентами
Сума із нарахованими на неї процентами може
де nt – тривалість послідовності періодів реінвестування;
it – ставки, за якими здійснюється реінвестування.
Приклад:
На суму 100000 грош. од. нараховується 10% річних. Проценти прості, точні. Розрахувати суму нарощування у кінці кварталу, якщо реінвестування відбувається щомісячно протягом 1 кварталу (в році 365 днів).
Слайд 43Дисконтування в Excel
Операція дисконтування полягає у розрахунку вихідної суми Р при
P = S/(1 + ni).
Для дисконтування в Excel є вбудована функція із категорії «Финансовые»
Приклад:
Платіжне зобов'язання сплатити через 60 днів 200000 грн. з відсотками, що нараховуються за ставкою простих відсотків I = 15% річних, було враховано за 10 днів до терміну погашення за обліковою ставкою 12%. Обчислити суму, одержувану при обліку (число днів у році 365).
Слайд 44Обчислення нарощування за складними процентами в Excel
Формула нарощування для складних процентів
S = P(1 + I)n,
де S – нарощена сума; I – річна ставка складних процентів; n – термін позики (кількість періодів).
Для обчислення нарощеної суми в Excel є вбудована функція БС із категорії «Финансовые»:
БС(Ставка; Кпер; Плт; Пс; Тип)
Для розв’язання зворотних задач в Excel є вбудовані функції СТАВКА, КПЕР (із категорії «Финансовые»:
СТАВКА(Кпер; Плт; Пс; Бс; Тип) – вираховує ставку;
КПЕР(Ставка; Плт; Пс; Бс; Тип) – вираховує кількість періодів.
Обчислення номінальної та ефективної ставки процентів в Excel
Нарахування процентів за номінальною ставкою здійснюється за формулою:
S = P(1 + j/m)N,
де N – число періодів нарахування, N=mn; j – номінальна річна ставка складних процентів; m – число нарахувань за рік.
Для обчислення ефективної ставки в Excel є вбудована функція ЭФФЕКТ(Номинальная_ставка; Количество_периодов) із категорії «Финансовые».
Для обчислення номінальної ставки при заданій ефективній в Excel є вбудована функція НОМИНАЛ(Эффективная_ставка; Количество_периодов) із категорії «Финансовые».
Слайд 45Обчислення нарощеної суми при змінній процентній ставці в Excel
Для обчислення в
БЗРАСПИС(Первичное; План),
де Первичное – поточне значення інвестицій; План – масив використовуваних процентних ставок.
Приклад:
Клієнт зробив внесок у банк в сумі 1 тис. грош. од. під 30% річних строком на 1 рік. Процентна ставка у першому кварталі складала 30% річних, в середині другого кварталу вона знизилась до 25%, на початку четвертого кварталу вона знову зросла до 30%. Яку суму отримає клієнт у кінці року?